Electromagnetics and wave propagationDGTD methods for the Maxwell equations on unstructured meshesLoulaFezouiStéphaneLanteriSergePipernoMaxwell systemtime domainstructured meshlocally refined meshconforming meshnon-conforming meshfinite volume methoddiscontinuous Galerkin methodstabilityElectromagnetic problems often involve objects with complex
geometries. Therefore, the use of unstructured tetrahedral meshes is
mandatory for many applications.
We have proposed
DGTD methods for the Maxwell equations on locally refined meshesAntoineBouquetNicolasCanouetAdrienCatellaLoulaFezouiSergePipernoStéphaneLanteriClaudeDedebanFrance Télécom R&D, center of La TurbieMaxwell systemtime domainstructured meshlocally refined meshconforming meshnon-conforming meshfinite volume methoddiscontinuous Galerkin methodstabilityElectromagnetic problems often involve objects of very different
scales. In collaboration with France Télécom R&D, we have studied
Discontinuous Galerkin Time Domain (DGTD) methods for the
numerical simulation of the three-dimensional Maxwell equations on locally
refined, possibly non-conforming meshes. We had proposed an explicit
scheme based on a classical Discontinuous Galerkin formulation which
is able to deal with structured non-conforming grids
The method is currently being reimplemented in a cartesian grid
setting and numerical parallel acceleration of this implementation will
be a part of the PhD thesis subject of Antoine Bouquet (completely
funded by France Telecom R&D). Other interesting questions are the
possibility to enhance accuracy and to couple with fictitious domain
methods.
Finite volume and discontinuous Galerkin type methods for frequency domain electromagneticsHugoFolStéphaneLanteriSergePipernoMaxwell equationsfrequency domainunstructured meshfinite volumediscontinuous Galerkincell centered schemeThe goal of this study, which started in October 2003 with the
doctoral thesis of Hugo Fol, is to extend the finite
volume
Computational bioelectromagneticsNicholasAyacheproject-team EpidaureGrégoryBeaumeIsabelleBlochENST ParisJasminBurguetENST ParisOlivierClatzproject-team EpidaureMaureenClercproject-team OdysséeGarryCohenproject-team OndesRenéDe SezeINERIS, center of Verneuil-en-HalatteClaudeDedebanFrance Télécom R&D, center of La TurbieHervéDelingetteproject-team EpidaureNajibGadiENST ParisPatrickJolyproject-team OndesStéphaneLanteriSteveOudotproject-team GeometricaTheodorePapadopouloproject-team OdysséeJean-PhilippePonsproject-team OdysséeSergePipernoGillesScarellaJoeWiartFrance Télécom R&D, center of Issy-les-Moulineauxmobile-phonenumerical dosimetrythermal effectsMRIimage processingMaxwell equationsstructured meshfinite difference time domainunstructured meshfinite volume time domainfinite element time domainProject-team Caiman is the coordinator of the
HEADEXP
Biological effects of microwave radiation have been investigated both
from the experimental and numerical viewpoints. Concerning numerical
modelling, the power absorption in a user head is computed using
discretized models built from clinical MRI data. The great majority of
such numerical studies have been conducted using the widely known FDTD
(Finite Difference Time Domain) method. In this method, the
whole computational domain is discretized using a structured
(cartesian) grid. Due to the possible straightforward implementation
of the algorithm and the availability of computational power, FDTD is
currently the leading method for numerical assessment of human
exposure to electromagnetic waves. However, limitations are still
seen, due to the rather difficult departure from the commonly used
rectilinear grid and cell size limitations regarding very detailed
structures of head tissues as well as of a handset which might be
essential for reliable compliance testing. So far, little attention
has been paid to the application of numerical methods able to deal with
unstructured grids that is, FETD (Finite Element Time Domain) and FVTD
(Finite Volume Time Domain) methods.
The HEADEXP project aims at filling the gap between human head MRI
images and the efficient and accurate numerical modelling of the
interaction of electromagnetic waves emitted by mobile phones on
biological tissues. This is made possible by the development of
appropriate image analysis tools and automated unstructured mesh
generation tools for the construction of realistic discretized human
head models. Then, a first objective is to use the resulting head
models to perform a dosimetric analysis of the radiated
electromagnetic wave. In HEADEXP, this analysis relies on the FETD
and FVTD solvers developed in the Caiman and Ondes project-teams. The
results of these solvers are compared with those of the routinely used
FDTD method for this task. A particular emphasis is put on the
ability of the solvers to take into account the heterogeneity of the
electromagnetic characteristics (conductivity, permittivity,
permeability tensors) of the underlying media. Starting from the
result of the numerical dosimetry analysis, a second objective of the
HEADEXP project is to study the thermal effects induced by the
dissipation of electric energy in the biological tissues. This
requires the numerical solution of an appropriate bioheat equation
that models heat transfers in biological tissues.
Finite volume method for seismic wave propagationMondherBenjemaaNathalieGlinsky-OlivierSergePipernoJeanVirieuxGéosciences AzurP-SV wave propagationvelocity-stress systemfinite volumecentered schemeNumerical methods for the propagation of seismic waves have been
studied for many years. Most of these numerical codes rely on
finite-element or finite-difference methods. Among the most
popular schemes, we can cite the staggered-grid-finite-difference
scheme proposed by J. Virieux
To study the P-SV wave propagation in an heterogeneous medium,
we solve the first-order hyperbolic system of elastic wave
equations (Virieux, 1986) in a vertical 2D medium, supposed linearly
elastic and isotropic (parameters for the medium are the density
 and the Lamé coefficients
and the Lamé coefficients  and
and  ).
This system having the same characteristics the Maxwell equations, we solve
it using an adaptation of the second-order centered leap-frog scheme
initially developed by M. Remaki
).
This system having the same characteristics the Maxwell equations, we solve
it using an adaptation of the second-order centered leap-frog scheme
initially developed by M. Remaki
The validation of this method has been continued by studying
the P-SV wave propagation in an homogeneous medium
with a horizontal free surface. Solutions have been compared to analytical
seismograms for horizontal and vertical
velocities
We are also interested in the simulation of a fault, dynamic or
preexistent. This problem has already been solved especially by
finite-difference methods for which the fault is represented by a set
of local sources following the fault's geometry. Using finite-volume
methods, two techniques can be proposed. The first one considers the
fault as a set of triangles and the solutions obtained have been
validated by cofrontation with results of the finite-difference method. A
second method, new and more original, consists of a representation of
the fault by a set of segments instead of elements. A study of the
total energy of the system provides a flux condition in the fault which
is stable and accurate. Satisfying results have been obtained for a
preexistent fault and we are now considering the case of a dynamic
fault.
We are also interested in the application of discontinuous Galerkin
type methods to the solution of these equations and in the extension
to the three-dimensional case.
Computational fluid dynamics and related problemsAcoustic waves propagation in a steady non-uniform flowMarcBernackiSergePipernolinearized Euler equationssteady non-uniform flowfinite volume methoddiscontinous Galerkin methodleap-frog time schemecentered fluxesabsorbing boundary conditionreflecting boundary conditionL2 stabilityunstructured meshesWe are currently studying the propagation of acoustic waves in a
steady inviscid flow. This subject is directly related to many
research themes of the project-team. Starting from a steady solution of
the Euler equations in a given configuration (geometry, mesh, flow), we aim
at propagating acoustic waves in this continuously heterogeneous
medium. This is done by simulating the propagation of very small
perturbations, following the linearized Euler equations. We then apply
in this context of wave-advection equations the same kind of
dissipation-free numerical methods which were developed by the team
for electromagnetics in the time domain.
A general discontinous Galerkin framework has been introduced for the
propagation of aeroacoustic perturbations of either uniform or non
uniform, steady solution of the three-dimensional Euler equations
Self-adaptive moving meshesMaudPoretSergePipernocomputational fluid dynamicshyperbolic conservation lawsfinite volumeunstructured dynamic meshmesh adaptationvariable topologyarbitrary Lagrangian-Eulerian formulationarbitrary explicit-implicit schememonotonicityTVD propertyWe have considered dynamic self-adaptative mesh methods for
solving hyperbolic linear or non-linear equations in one or two space
dimensions. These methods are based on two approaches: the
first relies on a moving mesh process without changing mesh topology,
the second consists in local and dynamical grid
refinement-coarsening. We employ a finite volume scheme based on
variable grids (moving and refined) with numerical Godunov-type
flows. The main originality consists in writing a finite volume method
on a variable topology, hence introducing appearing or disappearing finite
volumes (and writing finite volume formulations on possibly void
control volumes).
The solutions adopted in one-dimensional problems
Relaxation methods for the compressible Navier-Stokes equationsNathalieGlinsky-OlivierAlexandreErnCERMICSNavier-Stokes equationsrelaxation methodentropyEnskog-Chapman developmentreal gasfinite volumeGas flows arising in many engineering applications may be modeled
using the compressible Navier-Stokes equations. These equations
express the conservation of mass, momentum and energy and must be
completed by a thermodynamic model providing the pressure and the
temperature as functions of the conservative variables.
The simplest model is that of a thermally perfect and calorifically
perfect gas (TPCP, also referred to as polytropic ideal gas) in which,
firstly,
the pressure p is bilinear in the density  and the
specific internal energy
and the
specific internal energy  ,
,
p = ( -1)
-1)
 , where
, where  >1 is a constant
(which is also the ratio between calorific capacities at constant
pressure and volume) and secondly,
the temperature
>1 is a constant
(which is also the ratio between calorific capacities at constant
pressure and volume) and secondly,
the temperature T is linear in  and does not
depend on the density :
and does not
depend on the density :
 :
: 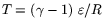 , where
, where R
is a constant given by the universal gas constant divided by the
molecular mass of the gas.
Because of its relative simplicity, the TPCP gas model has often been
considered in applications. Many robust Navier-Stokes
solvers based on this assumption exist ; some of them
involve finite volume discretizations in which the Riemann solver
explicitly relies upon the TPCP gas model.
Many gas flows require a more elaborate thermodynamic model
(for instance, polyatomic gas flows or high pressure flows).
The pressure and the temperature are then nonlinear functions of the
specific internal energy, while the pressure is still bilinear in the
density and the temperature. Such gases will be referred to as
thermally perfect (TP).
An attractive approach to incorporate complex pressure and temperature
laws in the numerical simulation of gas flows is to consider a
relaxation method. For the Euler equations, a relaxation method has
been derived recently by Coquel and Perthame
We have developed a relaxation method for the compressible
Navier-Stokes equations. The main difference with the Euler equations
is that because of the presence of diffusive fluxes, it is necessary
to account not only for pressure relaxation but also for temperature
relaxation. The new system is solved using a mixed finite
volume/finite element method applicable to unstructured triangular
meshes. The convective
fluxes are evaluated using a Roe scheme of order 3, thanks to a
combination of the MUSCL method and a  -scheme. For most complex
test cases, a recent more robust limiter designed for the Euler
equations
-scheme. For most complex
test cases, a recent more robust limiter designed for the Euler
equations
Attention has been focused on the study of
the interaction of a reflected shock wave with
the incident boundary layer in a shock tube for two values of the
Reynolds number Re = 200 and Re = 1000, and we have compared our
solutions with published results Re = 1000 for which the flow is very
complex. We have also investigated the case where the adiabatic
exponent is temperature dependent and follows the vibrational
model. Because of the strong temperature variations present in the
flow, non-linearities arising in the adiabatic exponent yield a
sizeable impact on the flow dynamics. The agreement between the
results obtained with the relaxation method and those of an extended
real gas Navier-Stokes code appears to be excellent.
Domain decomposition and coupling algorithmsConvergence analysis of additive Schwarz for the Euler equationsVictoritaDoleanUniversité d'Evry et CMAP, École PolytechniqueStéphaneLanteriFrédéricNatafCMAP, École PolytechniqueEuler equationsdomain decompositionfinite volumeadditive Schwarzinterface conditionsWe are interested here in the design, analysis and evaluation of
domain decomposition methods for the solution of algebraic systems
resulting from the discretization of hyperbolic or mixed
hyperbolic/parabolic systems of partial differential equations such as
those modelling compressible fluid mechanics problems.
This activity is carried out in the context of a collaboration that
was initiated during the doctoral thesis of Victorita
Dolean
Time and space multi-scale approaches for the 1D and 2D Maxwell/acoustic equationsSergePipernoone-dimensional Maxwell systemtwo-dimensional acoustics equationstime domainfinite volume methoddiscontinuous Galerkin methodcentered fluxleap-frog time schemecoupling algorithmsubcyclingstabilitylocally refined meshAiming at solving the Maxwell equations in the time domain with locally
refined grids (structured or unstructured), we study the possibility
of using both space and time locally refined subdomains. We are
developing in two space dimensions for acoustics the numerical
algorithms proposed in 1D
Plasmic environment of satellitesMartineChane-YookAnneNouriLATP, CMI, Université de ProvenceFrédéricPoupaudSergePipernoSébastienClercAlcatel Spaceplasmaplasmic propulsionmagnetosphereionizationVlasov-Poisson equations
model couplingIn collaboration with Alcatel Space, we study problems related to
the electrostatic charge of satellites. These charges are received
periodically from the sun and from the plasmic propulsors (which will
be more used in a near future). The presence of these charged
particles can lead to undesired potential gaps and eventually to
electrostatic discharges (able to destroy some parts of solar energy
generators). Following the pioneering work of Olivier Chanrion, which
provided a software for the pseudo-transient two-dimensional
axisymmetric Vlasov-Poisson equations, Martine Chane-Yook is aiming
at developing a three-dimensional code, including the same features
and starting from a basis developed by Sébastien Clerc at Alcatel.
During the last year, the use of infinite elements at the outside
boundary for the Poisson equation has been validated in three space
dimensions. At the same time, we have examined the hypotheses under
which the spatial volumic charge had to be taken into
account or not. If needed, it is computed using a back-trajectories algorithm
which is also used for the computation of currents impacting the
surface of the satellite. Finally, an algorithm for the determination
of the electric potential of conductors (starting from magnetospheric
currents, themselves evaluated using back-trajectories) has been
proposed, where relaxation has been added to improve iterative
convergence
High performance parallel and distributed computingLarge-scale three-dimensional electromagnetics calculationsMarcBernackiLoulaFezouiStéphaneLanteriSergePipernoaeroacousticselectromagneticstime domainunstructured meshfinite volumediscontinuous Galerkincell centered schemeparallel computingdomain partitioningmessage passingMPIThe numerical simulation of realistic three-dimensional
electromagnetics and aeroacoustics problems typically translates into
the processing of very large amounts of data, especially for external
problems. This is essentially the result of two antagonistic
parameters: the characteristic space step of the mesh and the
computational domain size. For high frequency phenomena, the space
step can be very small while the artificial boundaries of the
computational domain are located near the scattering object whereas an
opposite situation is obtained for low frequency phenomena. Several
numerical techniques can be considered in order to handle this
problem to some extent such as, for instance, the reduction of the computational
domain size through the use of perfectly matched layers. However,
these numerical modelling adaptations are generally not sufficient and
the computational power and memory capacity that are required for the
simulation of realistic problems are such that the use of parallel
computing platforms becomes essential. With respect to this need, we
have developed parallel versions of our finite volume and
discontinuous Galerkin methods for the solution of elctromagnetic and
aeroacoustic wave propagation problems on unstructured tetrahedral
meshes
Grid computing for the simulation of large-scale electromagnetic problemsFrançoiseBaudeproject-team OasisDenisCaromelproject-team OasisChristianDelbeproject-team OasisSaïdEl KasmiFabriceHuetproject-team OasisStéphaneLanteriRomainQuiliciproject-team OasisGrid computinghigh performance computingparallel and distributed computingProActive java librarytime-domain Maxwell equationsFor scientific applications such as those considered in project-team
Caiman, the effective use of a heterogeneous, distributed, computing
platform (i.e. a grid computing platform) requires new studies that
must address several topics ranging from computer science concerns to
more application related issues. This is for example the case for the
development of numerical simulation tools that will be able to exploit
several high performance computers (clusters of PCs, SMPs)
geographically distributed. Indeed, from the computer science
viewpoint, it is necessary to devise new parallelization strategies
that will take into account the heterogeneity of the computational
nodes (CPUs) and the interconnection networks. This characteristics
could also be considered at the numerical modelling level through the
design of hierarchical PDE solvers based on domain decomposition
principles. However, grid computing also motivates the development of
new generation collaborative tools that will allow several people
located in different sites, to follow or even act on a running
numerical simulation. Such a tool will ideally be based on different
modules (PDE solver, visualization server, geometric modeler, etc.)
that will be coupled and distributed on special purpose computers
(clusters of PCs, SMPs, high performance graphical server).
Both applications discussed above could be designed as
component based distributed applications and, in order to do so, it
would be
necessary to adopt an appropriate programming paradigm. In 2002, we
have initiated a collaboration with computer scientists from the
project-team Oasis at INRIA Sophia Antipolis whose general objective
is to apply distributed object-oriented programming principles to the
context of computational electromagnetics applications. Two main
activities have been considered so far.
For what concerns numerical simulation tools, we have developed
JEM3D
Beside this activity, we are also working on the development of a
collaborative tool for the interactive visualization of
three-dimensional numerical simulation
results
![]()
![]()