Scientific FoundationsKinetic models for plasma and beam physicsplasma physicsbeam physicskinetic modelsreduced modelsVlasov equationmodelingmathematical analysisasymptotic analysisexistenceuniquenessPlasmas and particle beams can be described by a hierarchy of models including
N-body interaction, kinetic models and fluid models. Kinetic models in particular
are posed in phase-space and involve specific difficulties. We perform a mathematical
analysis of such models and try to find and justify approximate models using asymptotic analysis.
Models for plasma and beam physicsThe plasma state can be considered as the fourth state of matter, obtained for example by bringing a gas to a very high temperature (104K or more). The thermal energy of the molecules and atoms constituting the gas is then sufficient
to start ionization when particles collide. A globally neutral gas of neutral and charged particles, called plasma, is then obtained.
Intense charged particle beams, called nonneutral plasmas by some authors, obey similar physical laws.
The hierarchy of models describing the evolution of charged particles within a plasma or a particle beam includes N-body models where each particle interacts directly with all the others, kinetic models based on a statistical description of the particles and fluid models valid when the particles are at a thermodynamical equilibrium.
In a so-called kinetic model, each particle species s in a plasma or a particle beam is described by a distribution function fs(x, v, t) corresponding to the statistical average of the particle distribution in phase-space corresponding to many realisations of the physical system under investigation.
The product fsdxdv is the average number of particles of the considered species, the position and velocity of which are located in a bin of volume
dxdv centered around (x, v).
The distribution function contains a lot more information than what can be obtained
from a fluid description, as it also includes information about the velocity distribution of the particles.
A kinetic description is necessary in collective plasmas where the distribution function is very different from the Maxwell-Boltzmann (or Maxwellian) distribution which corresponds to the thermodynamical equilibrium, else a fluid description is generally sufficient. In the limit when collective effects
are dominant with respect to binary collisions, the corresponding kinetic equation
is the Vlasov equation
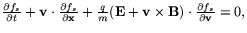
which expresses that the distribution function f is conserved along the particle trajectories which are determined by their motion in their mean electromagnetic field.
The Vlasov equation which involves a self-consistent electromagnetic field needs to be coupled to the Maxwell equations in order to compute this field
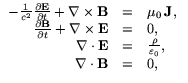
which describe the evolution of the electromagnetic field generated by the charge
density
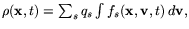
and current density
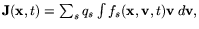
associated to the charged particles.
When binary particle-particle interactions are dominant with respect to the mean-field effects then the distribution function f obeys the Boltzmann equation
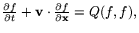
where Q is the nonlinear Boltzmann collision operator.
In some intermediate cases, a collision operator needs to be added to the Vlasov equation.
The numerical resolution of the three-dimensional Vlasov-Maxwell system represents a considerable challenge due to the huge size of the problem. Indeed, the Vlasov-Maxwell system is non linear and posed in phase space. It thus depends on seven variables: three configuration space variables, three velocity space variables and time,
for each species of particles. This feature makes essential the use every possible option to find a reduced model wherever possible, in particular when there are geometrical symmetries or small terms which can be neglected.
Mathematical and asymptotic analysis of kinetic modelsThe mathematical analysis of the Vlasov equation is essential for a thorough understanding of the model as well for physical as for numerical purposes. It has attracted many researchers
since the end of the 1970s. Among the most important results which have been
obtained, we can cite the existence of strong and weak solutions of the Vlasov-Poisson system by Horst and Hunze
Many questions concerning for example uniqueness or existence of strong solutions for the three-dimensional Vlasov-Maxwell system are still open. Moreover, their is a realm of approached models that need to be investigated. In particular, the Vlasov-Darwin model for which we could recently prove the existence of global solutions for small initial data
On the other hand, the asymptotic study of the Vlasov equation in different physical situations is important in order to find or justify reduced models. One situation of major importance in Tokamaks, used for magnetic fusion as well as in atmospheric plasmas, is the case of a large external magnetic field used for confining the particles.
The magnetic field tends to incurve the particle trajectories who eventually, when the
magnetic field is large, are confined along the magnetic field lines. Moreover, when
an electric field is present, the particles drift in a direction perpendicular to
the magnetic and to the electric field. The new time scale linked to the cyclotron
frequency, which is the frequency of rotation around the magnetic field lines,
comes in addition to the other time scales present in the system like the plasma frequencies of the different particle species. Thus, many different time scales
as well as length scales linked in particular to the different Debye length are present
in the system. Depending on the effects that need to be studied, asymptotic techniques
allow to find reduced models.
In this spirit, in the case of large magnetic fields, recent results have been obtained
by Golse and Saint-Raymond
Another important asymptotic problem yielding reduced models for the Vlasov-Maxwell system is the fluid limit of
collisionless plasmas. In some specific physical situations, the infinite system
of velocity moments of the Vlasov equations can be close after a few of them,
thus yielding fluid models.
Development of simulation toolsNumerical methodsVlasov equationunstructured gridsadaptivitynumerical analysisconvergencesemi-Lagrangian methodThe development of efficient numerical methods is essential for the simulation of plasmas and beams. Indeed, kinetic models are posed in phase space and thus the number of dimensions is doubled. Our main effort lies in developing methods using
a phase-space grid as opposed to particle methods. In order to make such methods
efficient, it is essential to consider means for optimizing the number of mesh points.
This is done through different adaptive strategies. In order to understand the methods,
it is also important to perform their mathematical analysis.
IntroductionThe numerical integration of the Vlasov equation is one of the key
challenges of computational plasma physics. Since the early days of this
discipline, an intensive work on this subject has produced many different
numerical schemes. One of those, namely the Particle-In-Cell (PIC) technique, has been
by far the most widely used. Indeed it belongs to the class of Monte Carlo particle methods
which are independent of dimension and thus become very efficient when dimension increases
which is the case of the Vlasov equation posed in phase space.
However these methods converge slowly when the number of particles increases, hence if the complexity of grid based methods can be decreased, they can be the better choice in some situations.
This is the reason why one of the main challenges we address is the development and analysis of adaptive grid methods.
Convergence analysis of numerical schemesExploring grid based methods for the Vlasov equation, it becomes obvious that
they have different stability and accuracy properties. In order to fully understand
what are the important features of a given scheme and how to derive schemes with
the desired properties, it is essential to perform a thorough mathematical analysis
of scheme, investigating in particular its stability and convergence towards the
exact solution.
The semi-Lagrangian methodThe semi-Lagrangian method consists in computing a numerical approximation
of the solution of the Vlasov equation
on a phase space grid by using the
property of the equation that the distribution function f is conserved along
characteristics. More precisely, for any times s and t, we have
fxvtfXsxvtVsxvts
where (X(s;x, v, t), V(s;x, v, t)) are the characteristics of the Vlasov equation which are solution of the system of ordinary differential
equations
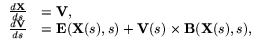
with initial conditions X(t) = x, V(t) = v.
From this property, fn being known one can induce a numerical method for computing the
distribution function fn + 1 at the grid points (xi, vj) consisting in the
following two steps:
For all i, j, compute the origin of the characteristic ending at xi, vj,
i.e. an approximation of X(tn;xi, vj, tn + 1), V(tn;xi, vj, tn + 1).
As
fn + 1xivjfnXtnxivjtn + 1Vtnxivjtn + 1
fn + 1 can be computed by interpolating fn which is known at the
grid points at the points X(tn;xi, vj, tn + 1), V(tn;xi, vj, tn + 1).
This method can be simplified by performing a time-splitting separating the advection
phases in physical space and velocity space, as in this case the characteristics
can be solved explicitly.
Adaptive semi-Lagrangian methodsUniform meshes are most of the time not efficient to solve a problem in plasma physics or beam physics as the distribution of particles is evolving a lot as well in space as in time during the simulation. In order to get optimal complexity, it is essential to use
meshes that are fitted to the actual distribution of particles.
If the global distribution is not uniform in space but remains locally mostly the same
in time, one possible approach could be to use an unstructured mesh of phase
space which allows to put the grid points as desired.
Another idea, if the distribution evolves a lot in time is to use a different grid at each
time step which is easily feasible with a semi-Lagrangian method.
And finally, the most complex and powerful method is to use a fully adaptive mesh
which evolves locally according to variations of the distribution function in time.
The evolution can be based on a posteriori estimates or on multi-resolution techniques.
Particle-In-Cell codesThe Particle-In-Cell method
Maxwell's equations in singular geometryThe Singular Complement MethodThe solutions to Maxwell's equations are a priori defined in a function space
such that the curl and the divergence are square integrable and
that satisfy
the electric and magnetic boundary conditions.
Those solutions are in fact smoother (all the derivatives are square integrable)
when the boundary of the domain is smooth or convex. This is no
longer true when the domain exhibits non-convex geometrical singularities
(corners, vertices or edges).
Physically, the electromagnetic field tends to infinity in the neighbourhood
of the reentrant singularities, which is a challenge to the usual finite
element methods. Nodal elements cannot converge towards the physical solution.
Edge elements demand considerable mesh refinement in order to represent those
infinities, which is not only time- and memory-consuming, but potentially
catastrophic when solving instationary equations: the CFL condition then
imposes a very small time step. Moreover, the fields computed by edge elements
are discontinuous, which can create considerable numerical noise when the
Maxwell solver is embedded in a plasma (e.g. PIC) code.
In order to overcome this dilemma, a method consists in splitting the solution
as the sum of a regular part, computed by
nodal elements, and a singular part which we relate to singular
solutions of the
Laplace operator, thus allowing to calculate a local analytic representation.
This makes it possible to compute the solution precisely without having
to refine the mesh.
This Singular Complement Method (SCM) had been developed
An especially interesting case is axisymmetric geometry.
This is still a 2D geometry, but more realistic than the plane case; despite
its practical interest, it had been subject to much fewer theoretical
studies
Other results, extensions.As a byproduct, space-time regularity results were obtained
for the solution to
time-dependent Maxwell's equation in presence of geometrical singularities
in the plane and axisymmetric cases
Large size problemsParallelismdomain decompositionGRIDcode transformationThe applications we consider lead to very large size computational problems for which we need to apply modern computing techniques enabling to use efficiently many computers including traditional high performance parallel computers and computational grids.
IntroductionThe full Vlasov-Maxwell system yields a very large computational problem
mostly because the Vlasov equation is posed in six-dimensional phase-space.
In order to tackle the most realistic possible physical problems, it is important
to use all the modern computing power and techniques, in particular parallelism
and grid computing.
Parallelization of numerical methodsAn important issue for the practical use of the method we develop is their parallelization.
We address the problem of tuning these methods to homogeneous or heterogeneous architectures
with the aim of meeting increasing computing ressources requirements.
Most of the considered numerical methods apply a series of operations
identically to all elements of a geometric data structure: the mesh of phase space.
Therefore these methods intrinsically can be viewed as a data-parallel algorithm.
A major advantage of this data-parallel approach derives from its scalability.
Because operations may be applied identically to many data items in parallel,
the amount of parallelism is dictated by the problem size.
Parallelism, for such data-parallel PDE solvers, is achieved by partitionning the mesh
and mapping the submeshes onto the processors of a parallel architecture.
A good partition balances the workload while minimizing the communications overhead.
Many interesting heuristics have been proposed
to compute near-optimal partitions of a (regular or irregular) mesh.
For instance, the heuristics based on space-filing curves
Adaptive methods include a mesh refinement step and
can highly reduce memory usage and computation volume.
As a result, they induce a load imbalance and require
to dynamically distribute the adaptive mesh.
A problem is then to combine distribution
and resolution components of the adaptive methods
with the aim of minimizing communications.
Data locality expression is of major importance for solving such problems.
We use our experience of data-parallelism and the underlying concepts
for expressing data locality
As a general rule, the complexity of adaptive methods
requires to define software abstractions
allowing to separate/integrate the various components
of the considered numerical methods (see
Another key point is the joint use of heterogeneous architectures and adaptive meshes.
It requires to develop new algorithms which include new load balancing techniques.
In that case, it may be interesting to combine several
parallel programming paradigms, i.e. data-parallelism with other lower-level ones.
Moreover, exploiting heterogeneous architectures
requires the use of a runtime support associated with a programming interface
that enables some low-level hardware characteristics to be unified.
Such runtime support is the basis for heterogeneous algorithmics.
Candidates for such a runtime support may be specific implementations of MPI
such as MPICH-G2 (a grid-enabled MPI implementation
on top of the GLOBUS tool kit for grid computing
Our general approach for designing efficient parallel algorithms
is to define code transformations at any level.
These transformations can be used to incrementally tune codes
to a target architecture and they warrant code reusability.
Scientific visualization of plasmas and beamsVisualization of multi-dimensional data and more generally of scientific data
has been the object of numerous research projects in computer graphics.
The approaches include visualization of three-dimensional scalar fields looking at
iso-curves and iso-surfaces. Methods for volume visualization, and methods based on points and flux visualization techniques and vectorial fields (using textures) have also
been considered. This project is devoted to specific techniques for fluids and
plasmas and needs to introduce novel techniques for the visualization of the phase-space which has more than three dimensions.
Even though visualization of the results of plasma simulations is an essential tool for the physical intuition, today's visualization techniques are not always well adapted tools, in comparison with the complexity of the physical phenomena to understand. Indeed the volume
visualization of these phenomena deals with multidimensional data sets and sizes nearer to terabytes than megabytes. Our scientific objective is to appreciably improve the reliability of the numerical simulations thanks to the implementation of suitable visualization techniques. More precisely, to study these problems, our objective is to develop new physical, mathematical and data-processing methods in scientific visualization: visualization of larger volume data-sets, taking into account the temporal evolution. A global access of data through 3D visualization is one
of the key issues in numerical simulations of thermonuclear fusion phenomena. A better representation of the numerical results will lead to a better understanding of the physical problems. In addition, immersive visualization helps to extract the complex structures that appear in the plasma. This work is related to a real integration between numerical simulation and scientific visualization.
Thanks to new methods of visualization, it will be possible to detect the zones of numerical interest, and to increase the precision of calculations in these zones. The integration of this dynamical side in the pipeline "simulation then visualization"
will not only allow scientific progress in these two fields, but also will support the installation of a unique process "simulation-visualization".
Application DomainsThermonuclear fusionInertial fusionmagnetic fusionITERparticle acceleratorslaser-matter interactionControled fusion is one of the major prospects for a long term source of energy.
Two main research directions are studied: magnetic fusion where the plasma is confined in tokamaks using large external magnetic field and inertial fusion where the plasma is confined thanks to intense laser or particle beams. The simulation tools we develop apply for both approaches.
Controlled fusion is one of the major challenges of the 21st century that can answer the need for a long term source of energy that does not accumulate wastes and is safe.
The nuclear fusion reaction is based on the fusion of atoms like Deuterium and Tritium. These can be obtained from the water of the oceans that is widely available and the reaction does not produce long-term radioactive wastes, unlike today's nuclear
power plants which are based on nuclear fission
Two major research approaches are followed towards the objective of fusion based
nuclear plants: magnetic fusion and inertial fusion. In order to achieve a sustained fusion reaction, it is necessary to confine sufficiently the plasma for a long enough time.
If the confinement density is higher, the confinement time can be shorter but the product needs to be greater than some threshold value.
The idea behind magnetic fusion is to use large toroidal devices called tokamacs in which the plasma can be confined thanks to large applied magnetic field.
The international project ITER[http://www.iter.gouv.fr] is based on this idea and aims to build a new tokamak which could demonstrate the feasibility of the concept.
The inertial fusion concept consists in using intense laser beams or particle beams
to confine a small target containing the Deuterium and Tritium atoms.
The Laser Mégajoule which is being built at CEA in Bordeaux will
be used for experiments using this approach.
Our work in modelling and numerical simulation of plasmas and particle beams
can be applied to problems like
laser-matter interaction in particular for particle accelerators,
the study of parametric instabilities (Raman, Brillouin), the fast ignitor concept in the
laser fusion research. Another application is devoted to the
development of Vlasov gyrokinetic codes in the framework of the magnetic
fusion programme.
Finally, we work in collaboration with
the American Heavy Ion Fusion Virtual National Laboratory, regrouping teams
from laboratories in Berkeley, Livermore and Princeton on the development of
simulation tools for the evolution of particle beams in accelerators.
NanophysicsKinetic models like the Vlasov equation can also be applied for the study of
large nano-particles as approximate models when ab initio approaches are too
costly.
In order to model and interpret experimental results obtained with
large nano-particles, ab initio methods cannot be employed as they
involve prohibitive computational times. A possible alternative
resorts to the use of kinetic methods originally developed both in
nuclear and plasma physics, for which the valence electrons are
assimilated to an inhomogeneous electron plasma. The LPMIA (Nancy)
possesses a long experience on the theoretical and computational
methods currently used for the solution of kinetic equation of the
Vlasov and Wigner type, particularly in the field of plasma
physics.
Using a Vlasov Eulerian code, we have investigated in detail the
microscopic electron dynamics in the relevant phase space. Thanks
to a numerical scheme recently developed by Filbet et al.
The nano-particle was excited by imparting a small velocity shift
to the electron distribution. In the small perturbation regime, we
recover the results of linear theory, namely oscillations at the
Mie frequency and Landau damping. For larger perturbations
nonlinear effects were observed to modify the shape of the
electron distribution.
For longer time, electron thermalization is observed: as the
oscillations are damped, the center of mass energy is entirely
converted into thermal energy (kinetic energy around the Fermi
surface). Note that this thermalization process takes place even
in the absence of electron-electron collisions, as only the
electric mean-field is present.
New ResultsReduced modelling of plasmasSimonLabruniePierreBertrandIn collaboration with J.A. Carrillo (Universitat Autònoma de Barcelona)
we have studied mathematically a reduced kinetic model for laser-plasma
interaction. Global existence and uniqueness of solutions and the stability of
certain equilibria were obtained
Despite its one-dimensional character, this system is strongly
non-linear and already embeds some features of higher-dimensional,
relativistic Vlasov–Maxwell systems. Thus it had been subject to many physical
Convergence of semi-Lagrangian methods NicolasBesseMichelMehrenbergerThe convergence of several semi-Lagrangian numerical schemes for the one-dimensional Vlasov-Poisson equations has been proved and error estimates given in the case of several interpolation schemes:
linear interpolating polynomials on an unstructured mesh of phase-space, f
on a uniform grid of phase-space
Convergence of discontinuous Galerkin methods for the MHD system NicolasBesseWe developed and proved, in collaboration with D. Kröner (Freiburg, Germany), the convergence of a
locally divergence free discontinuous Galerkin finite element method for the induction equations
of the MHD system
WENO simulations of plasmasSimonLabrunieVladimirLatochaWe are presently working on the definition
and parallelization of a WENO code for the simulation of laser-plasma
interactions. It is based on the 1D code already used in
Moment conservation in the adaptive method based on interpolating waveletsMichaëlGutnicMatthieuHaefeléEricSonnendrückerThe first version of our adaptive method did not exactly conserve mass, when
grid points where removed. Even though we can always get sufficient conservation
by lowering the threshold for removing grid points, this is not efficient for some problems.
Therefore, we developed a procedure enabling to conserve any desired number of moments.
The idea is based on the
lifting procedure introduced by Sweldens
Moment conservation in the adaptive method based on hierarchical finite elementsOlivierHoenenMichelMehrenbergerIsabelleMetzmeyerEricViolardWe currently investigate techniques for mass conservation in the hierarchical finite element method.
The basic idea here is associating
an average mass with each cell of the dyadic mesh.
During time evolution, mass conservation is achieved
by redistributing the mass amongst cells.
The mass of each cell of the predicted mesh is determined
from the mass contribution of the backward advected cells
of the initial mesh.
Optimization of ObiwanMichaëlGutnicMatthieuHaefeléGuillaumeLatuA first sequential simulator was developed using a numerical scheme based on
wavelets. From one time step to the other, two advections in variables x and
v are performed on a given space containing N points. Only a percentage p of
all the points (x, v) are effectively advected in the considered space,
as the adaptive wavelet method allows us to reconstruct the remaining points if
necessary. For small values of p, one can expect to reduce the total
computing cost because the advection concerns only pN points instead of N.
Nevertheless, the use of this method has an overhead since we have to
deal with the wavelet coefficients after each advection. In order to obtain an
efficient application, we considered the complexity of the advection
algorithm, and of the overhead. We performed a reduction of the overhead in
several ways. We first reduced the complexity in memory consumption and
improved the use of cache memory. We replaced the data structure used to keep
the wavelet coefficient (a hashtable) with a sparse data structure that has
better properties in term of access time (for reading and writing).
Furthermore, we evaluated a possible parallelization of the application. The
dependencies between data and computation are currently under evaluation.
Because of access of coefficients at different levels, necessary with the wavelet method, data locality is
not very good. Therefore, we will probably consider a parallel version of the application
that will use a shared memory machine. Thus, the wavelet coefficients will
be easily accessible from each processor.
Parallelization of YodaOlivierHoenenMichelMehrenbergerEricViolardWe investigated the parallel implementation of an adaptive method
based on hierarchical finite elements.
The underlying numerical method uses a dyadic mesh which is particularly
well suited to manage data locality. We have developed an adapted data
distribution pattern based on a division of the computational domain into
regions and integrated a load balancing mechanism which periodically
redefines regions to follow the evolution of the physics.
In order to reduce communications, the regions
which are built should be connex. We use the Hilbert's
space filling curve to achieve this goal.
Experimental results show the good efficiency of our code and confirm
the adequacy of our implementation choices.
We are also looking at simplifications of the ``forward-backward'' scheme:
We investigate a new numerical method with a simpler
time evolution scheme: in this new scheme,
the compressed mesh at next time step
is predicted directly. Only backward advections are performed.
Forward advections and compression phase
are eliminated from the old scheme.
The notion of regions may advantageously be reused
for defining a suitable load balancing mechanism.
Another issue addresses targeting of heterogeneous parallel architectures.
We are also extending the Yoda code to
4D phase-space. In order to validate the simulations we shall
compare them with simulations performed with Vador
which uses a uniform dense mesh and
is based on a conservative method. We want to characterize the advantages
of a given method relatively to the others. Our experiments
show that this could depend on the test case and
the required level of accuracy. Better implementations could be
obtained by integrating several methods together.
Numerical experiments of stimulated Raman scattering using semi-lagrangian Vlasov-Maxwell codesAlainGhizzoPierreBertrandThierryRéveilléNonlinear wave-wave interactions are primary mechanisms by which nonlinear
fields evolve in time. Understanding the detailed interactions between
nonlinear waves is an area of fundamental physics research in classical
field theory, hydrodynamics and statistical physics. A large amplitude
coherent wave will tend to couple to the natural modes of the medium
it is in and transfer energy to the internal degrees of freedom of
that system. This is particularly so in the case of high power lasers
which are monochromatic, coherent sources of high intensity radiation.
Just as in the other states of matter, a high laser beam in a plasma
can give rise to stimulated Raman and Brillouin scattering (respectively
SRS and SBS). These are three wave parametric instabilities where
two small amplitude daughter waves grow exponentially at the expense
of the pump wave, once phase matching conditions between the waves
are satisfied and threshold power levels are exceeded. The illumination
of the target must be uniform enough to allow symmetric implosion.
In addition, parametric instabilities in the underdense coronal plasma
must not reflect away or scatter a significant fraction of the incident
light (via SRS or SBS), nor should they produce significant levels
of hot electrons (via SRS), which can preheat the fuel and make its
isentropic compression far less efficient. Understanding how these
deleterious parametric processes function, what non uniformities and
imperfections can degrade their strength, how they saturate and interdepend,
all can benefit the design of new laser and target configuration which
would minimize their undesirable features in inertial confinement
fusion. Clearly, the physics of parametric instabilities must be well
understood in order to rationally avoid their perils in the varied
plasma and illumination conditions which will be employed in the National
Ignition Facility or LMJ lasers. Despite the thirty-year history of
the field, much remains to be investigated.
For these reasons, we have investigated Vlasov-Maxwell numerical experiments
for realistic plasmas in collaboration of the group of Dr B. Afeyan
of Polymath research Inc. (in an international collaboration program
of the Department of Energy of USA). Our studies so far indicate
that a promising way to deter these undesirable processes is by instigating
the externally controlled creation of large amplitude plasma fluctuations
making the plasma an inhospitable host for the growth of coherent
wave-wave interactions. The area where we plan to focus most of our
attention is in Vlasov-Maxwell (semi-lagrangian) simulations in 1D.
In several works, see for example
Resolution of the Vlasov equation on a moving grid of phase-spaceStéphanieSalmonEricSonnendrückerThis work is performed in collaboration with Edouard Oudet (University of Chambéry).
We extended the idea of solving the Vlasov equation on moving grids of phase space.
In our first work
Coupling particles with a Maxwell solver in PIC codesRégineBarthelméEricSonnendrückerWhen using the classical charge and current deposition algorithms in PIC codes,
the continuity equation 
t +
+  ·
·J = 0 is not satisfied
at the discrete level. Therefore when using only Ampere and Faraday's laws to compute
the electromagnetic field, Gauss's law  ·
·E =  is violated over long time computations
yielding unphysical results. Specific current deposition techniques need to be introduced. The most
widely used is that of Villasenor and Buneman which works for linear deposition algorithms.
We extended this method to higher order deposition schemes and to non uniform meshes.
is violated over long time computations
yielding unphysical results. Specific current deposition techniques need to be introduced. The most
widely used is that of Villasenor and Buneman which works for linear deposition algorithms.
We extended this method to higher order deposition schemes and to non uniform meshes.
High order finite element method for the wave equationSébastienJundStéphanieSalmonEricSonnendrückerIn the frame of the DFG/CNRS project "Noise Generation in Turbulent Flows", we need to develop
very precise solvers for the acoustics wave equation on unstructured grids. This solver will then
be coupled to an Euler solver to compute the noise generation.
In collaboration with our partners from the University of Stuttgart in Germany we want to
compare the efficiency of high order solvers based on continuous finite elements to high order
solvers based on the discontinuous Galerkin method. In order for the finite element solvers to
be efficient, we developed a new strategy to lump the mass matrix which can be applied at any
order. It has already been implemented for 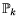 elements with
elements with k 6.
6.
Maxwell's equation in singular geometrySimonLabrunieWe have been carrying on the joint work with P. Ciarlet's team
at ENSTA and J. Zou (Chinese University of Hong-Kong). Our
Singular Complement Method (SCM) has been applied to simple,
but genuinely three-dimensional situations, namely prismatic and
axisymmetric domains with arbitrary data. Complete convergence proofs
and error estimates have been obtained, and numerical tests have been
performed in the electrostatic case
Transport equationsJeanRocheDidierSchmittThis work consists in the theoretical and numerical analysis of transport equations in collaboration with G. Jeandel and F.
(LEMTA).
Our main application is the propagation of heat by radiation and conduction in so-called semi-transparent media like those used for the isolation of houses or satellites.
This project, that started during the thesis of F. Asllanaj, has yielded many theoretical results: existence and uniqueness of the solution of the considered model as well as a priori estimates of the behavior of the solution (the luminance). This results can be considered new even from a physics point of view.
From a numerical point of view several algorithms have been conceived and implemented. Moreover their features (convergence, accuracy) have been analyzed
We are now developing a two dimensional version using domain decomposition methods. We are also interested in the coupled problem between radiation and Navier Stokes equation.
Domain decomposition for the resolution of non linear equationsJeanRocheThis a joint work with N. Alaa, Professor at the Marrakech Cadi Ayyad University.
The principal objective of this work is to study existence, uniqueness and present a
numerical analysis of weak solutions for a quasi-linear elliptic problem that arises in
biological, chemical and physical systems. Various methods have been
proposed for study the existence, uniqueness, qualitative properties and
numerical simulation of solutions.
We were particularly interested in situations involving irregular and arbitrarily growing data
(
Another approach studied here is the numerical approximation of the solution
to the problem. The most important difficulties are in this
approach the uniqueness and the blowup of the solution.
The general algorithm for numerical solution of this equations is one
application of the Newton method to the discretized version of the problem.
However, in our case the matrix which appears in the Newton
algorithm is singular.
To overcome this difficulty we introduced a domain decomposition to compute
an approximation of the iterates by the resolution of a
sequence of problems of the same type as the original problem in subsets of the given computational
domain.
This domain decomposition method coupled with a Yosida approximation of the non linearity
allows us to compute a numerical solution, see (
Interactive 4D+t visualization of a plasmaChristopheMionFlorenceZaraJean-MichelDischlerWe developed a new interactive visualization technique for exploring plasma behaviors resulting from
4D+t numerical simulations on regular grids. It implements a new out-of-core 4D+t visualization technique, based on a "focus and context" approach using a hybrid data compression method. The originality of this work consists in coupling the 3D visualization with the progressive load and decompression of data in such a way that it still guaranties real-time frame rates even on low-end PCs while maintaining a high degree of numerical precision.
![]()
![]()
![]()
![]()
![]()