Scientific FoundationsNumerical methods for option pricing and hedging and calibration of financial assets modelsV.BallyE.ClémentB.JourdainA.Kohatsu HigaD.LambertonB.LapeyreJ.PrintemsD.PommierA.SulemE.TemamA.ZanetteMonte-CarloEuler schemesapproximation of SDEtree methodsquantizationMalliavin calculusfinite differencecalibrationEfficient computations of prices and hedges for derivative products
is a major issue for financial institutions.
Although this research activity exists for more that fifteen years
at both academy and bank levels, it remains a lot of challenging questions especially for exotic products pricing on interest rates
and portfolio optimization with constraints.
This activity in the Mathfi team is strongly related to the
development of the Premia software. It also motivates theoretical
researches both on Monte–Carlo methods and numerical analysis
of (integro) partial differential equations :
Kolmogorov equation, Hamilton-Jacobi-Bellman equations,
variational and quasi–variational inequalities (see
MonteCarlo methods.The main issues concern numerical pricing and hedging of European and
American derivatives and sensibility analysis. Financial modelling is
generally based on diffusion processes of large dimension (greater
than 10), often degenerate or on Lévy processes. Therefore, efficient numerical methods are required. Monte-Carlo simulations are widely used
because of their implementation simplicity. Nevertheless, efficiency
issues rely on tricky mathematical problems such as accurate
approximation of functionals of Brownian motion (e.g. for exotic
options), use of low discrepancy sequences for nonsmooth functions
.... Speeding up the algorithms is a major issue in the developement of MonteCarlo simulation (see the thesis of A. Kbaier).
We develop Montecarlo algorithms based on quantization trees and
Malliavin calculus. V. Bally, G. Pagès and J. Printems have developed quantization methods especially for the computation of American options
Approximation of stochastic differential equations.In the diffusion models, the implementation of Monte-Carlo methods generally
requires the approximation of a stochastic differential equation,
the most common being the Euler scheme. The error can then be controlled
either by the LP-norm or the probability transitions.
PDE-based methods.We are concerned with the numerical analysis of degenerate parabolic
partial differential equations, variational and quasivariational inequalities,
Hamilton-Jacobi-Bellman equations especially in the case when the discrete maximum principle is not valid and in the case of an integral term coming from possible jumps in the dynamics of the underlying processes.
In large dimension, we start to investigate sparse grid methods.
Model calibration.While option pricing theory deals with valuation of derivative instruments given a stochastic process for the underlying asset, model calibration is about identifying the (unknown) stochastic
process of the underlying asset given information about prices of options.
It is generally an ill-posed inverse problem which leads to optimisation
under constraints.
Application of Malliavin calculus in financeV.BallyM.P.BavouzetB.JourdainA.Kohatsu HigaD.LambertonB.LapeyreM.MessaoudA.SulemE.TemamA.ZanetteMalliavin calculusstochastic variations calculussensibility calculusgreek computationsThe original Stochastic Calculus of Variations, now called the
Malliavin calculus, was developed by Paul Malliavin in 1976
>From the beginning of the nineties, applications of the Malliavin
calculus in finance have appeared : In 1991 Karatzas and Ocone showed
how the Malliavin calculus, as further developed by Ocone and others,
could be used in the computation of hedging portfolios in complete
markets
Since then, the Malliavin calculus has raised increasing interest and
subsequently many other applications to finance have been found, such
as minimal variance hedging and Monte Carlo methods for option
pricing. More recently, the Malliavin calculus has also become a
useful tool for studying insider trading models and some extended
market models driven by Lévy processes or fractional Brownian motion.
Let us try to give an idea why Malliavin calculus may be a useful instrument for probabilistic numerical methods. We recall that the theory is based on an integration by parts formula
of the form 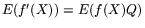 . Here
. Here X is a random variable which
is supposed to be ``smooth'' in a certain sense and non-degenerated. A
basic example is to take X = 
 where
where  is a
standard normally distributed random variable and
is a
standard normally distributed random variable and  is a strictly
positive number. Note that an integration by parts formula may
be obtained just by using the usual integration by parts in the presence of the
Gaussian density. But we may go further and take
is a strictly
positive number. Note that an integration by parts formula may
be obtained just by using the usual integration by parts in the presence of the
Gaussian density. But we may go further and take X to be an
aggregate of Gaussian random variables (think for example of the
Euler scheme for a diffusion process) or the limit of such simple functionals.
An important feature is that one has a relatively explicit expression for the weight Q
which appears in the integration by parts formula, and this expression
is given in terms of some Malliavin-derivative operators. Let us now look at one of the main consequenses of the integration by parts formula. If one considers the Dirac function 
x(y), then 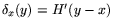 where
where H is the Heaviside function and the above
integration by parts formula reads E(
x(X)) = E(H(X-x)Q),
where E(
x(X)) can be interpreted as the density of the random variable X.
We thus obtain an integral representation of the density of the law of X.
This is the starting point of the approach to the density of the law
of a diffusion process: the above integral representation allows us to
prove that under appropriate hypothesis the density of X is smooth
and also to derive upper and lower bounds for it. Concerning
simulation by Monte Carlo methods, suppose that you want to compute
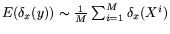 where
where
X1, ..., XM is a sample of X. As X has a law which is
absolutely continuous with respect to the Lebesgue measure, this will
fail because no Xi hits exactly x. But if you are able to
simulate the weight Q as well (and this is the case in many
applications because of the explicit form mentioned above) then you
may try to compute 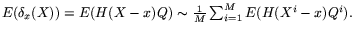 This basic remark formula leads to efficient methods to compute by a Monte Carlo method
some irregular quantities as derivatives of option prices with
respect to some parameters (the Greeks) or conditional
expectations, which appear in the pricing of American options
by the dynamic programming).
See the papers by Fournié et al
This basic remark formula leads to efficient methods to compute by a Monte Carlo method
some irregular quantities as derivatives of option prices with
respect to some parameters (the Greeks) or conditional
expectations, which appear in the pricing of American options
by the dynamic programming).
See the papers by Fournié et al
More recently the Malliavin calculus has been used in models of insider
trading.
The "enlargement of filtration" technique plays an
important role in the modelling of such problems and the Malliavin
calculus can be used to obtain general results about when and how
such filtration enlargement is possible. See the paper by P.Imkeller
in
Stochastic ControlJ.-Ph.Chancelier (ENPC)D.LefèvreM.MnifM.MessaoudB.Øksendal (Oslo University)A.SulemStochastic Controlsingular and impulse controlrisk-sensitive controlfree boudaryHamilton-Jacobi-Bellmanvariational and quasi-variational
inequalitiesStochastic control consists in the study of dynamical systems subject to random perturbations and which can be controlled in order to optimize some performance criterion function.
We consider systems following controlled diffusion dynamics possibly with jumps.
The objective is to optimize a criterion over all admissible strategies on a finite or infinite planning
horizon. The criterion can also be of ergodic or risk-sensitive type.
Dynamic programming approach leads to Hamilton-Jacobi-Bellman (HJB) equations
for the value function. This equation is integrodifferential in the case of
underlying jump processes (see
Optimal stopping problems such as American pricing lead to variational inequalities of obstacle type. In the case of singular control, the dynamic programming equation is a variational inequality, that is a system of partial differential inequalities. Singular control are used for example to model proportional transaction costs in portfolio optimisation.
The control process may also be of impulse type: in this case the state of the system jumps at some intervention times. The impulse control
consist in the sequence of instants and sizes of the
impulses. The associated dynamic programming equation is then a
Quasivariational inequality (QVI). These models are used for example in
the case of portfolio optimisation with fixed transaction costs.
Variational and quasivariational inequalities are free boundary problems.
The theory of viscosity solutions offers a rigourous framework for the study of
dynamic programming equations.
An alternative approach to dynamic programming is the study of
optimality conditions which lead to backward stochastic differential
equations for the adjoint state. See
We also study partial observation optimal control problems
Backward Stochastic Differential equationsM.C.QuenezM.Kobylanski (University of Marne la Vallée)BSDE
Backward Stochastic Differential equations (DSDE) are related to the stochastic
maximum principle for stochastic control problems. They also provide the prices of contingent claims in
complete and incomplete markets.
The solution of a BSDE is a pair of adapted processes (Y, Z) which satisfy
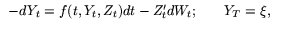
where f is the driver and  is the terminal condition
is the terminal condition
M.C. Quenez, N.El Karoui and S.Peng have established various
properties of BSDEs, in particular the links with stochastic control
(cf. B satisfies a BSDE with a linear driver and
a terminal condition equal to B. This is a dynamic way of pricing
which provides the price of B at all time and not only at 0.
In incomplete markets, the price process as defined by Föllmer and Schweizer
(1990) in ct, 0
t
T) corresponds
to the solution of a BSDE with terminal condition
 which can be a function of the terminal wealth, and a
driver
which can be a function of the terminal wealth, and a
driver f(t, ct, y) depending on the consumption ct. The standard utility
problem corresponds to a linear driver f of the type f(t, c, y) = u(c)-
ty, where u is a deterministic, non decreasing, concave
function and  is the discount factor.
is the discount factor.
In the case of reflected BSDEs, introduced in Y is forced to remain above some obstacle process. It satisfies
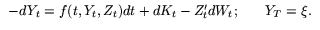
where K is a nondecreasing process.
For example the price of an American option satisfies a reflected BSDE where
the obstacle is the payoff. The optimal stopping time is the first time when
the prices reaches the payoff. (
SoftwareDevelopment of the software PREMIA for financial option computationsV.BallyAdelBen Haj YedderL.CaramellinoJ.Da FonsecaB.JourdainA.Kohatsu HigaB.LapeyreM.MessaoudN.Privault (University of La RochelleA.SulemE.TemamA.ZanettepricinghedgingcalibrationpriceroptionsWe develop a software called PREMIA designed for pricing and hedging options
on assets and interest rates and for calibration of financial models.
This software
Premia is thus concentrated on derivatives with rigorous numerical
treatment and didactic inclination.
Premia is developed in collaboration with a consortium of financial
institutions or departments: It is presently composed of:
IXIS CIB (Corporate & Investment Bank), CALYON, the Crédit Industriel et Commercial, EDF, GDF, Société générale and Summit.
History of PREMIA:
The development of Premia started in 1999. There exists now 6 releases.
Premia1, 2 and 4
contain finite difference algorithms, tree methods and Monte Carlo methods
for pricing and hedging European and American options on stocks in the Black-Scholes model in one and two dimension.
Premia3 is dedicated to Monte Carlo methods for American options
in large dimension. Moreover, it has an interface with the
software Scilab
Premia5 and 6 contain more sophisticated algorithms such as
quantization methods for American options
In 2004, the main development in the release Premia7 has consisted in implementing routines for pricing derivatives in interest rate models:
(Vasicek, Hull-White, CIR, CIR++,
Black-Karasinsky, Squared-Gaussian, Li, Ritchken, Sankarasubramanian
HJM, Bhar Chiarella HJM, BGM).
Moreover new algorithms for
calibrating in various models (stochastic volatility, jumps, ..) have
been implemented and numerical methods based on Malliavin calculus for
jump processes have been further explored.
Premia1, 2, 3, 4, 5, 6 have been delivered to the members of the bank consortium in
May 1999, December 1999, February 2001, February 2002, February 2003,
February 2004 respectively. Premia7 will be delivered in February
2005.
The next release, Premia8, under development in 2005, will be
dedicated to the pricing of credit risk derivatives and pricing
and calibration for
interest rate derivatives.
Premia3 and Premia4 can be downloaded from the web site:
[http://www-rocq.inria.fr/mathfi/Premia/index.html].
New ResultsMonte Carlo methods and stochastic algorithms Variance reduction methods in Monte Carlo simulationsB.ArounaB.LapeyreN.MoreniUnder the supervision of Bernard Lapeyre, B. Arouna has defended his
PHD thesis in which he shown that stochastics algorithms can be
efficiently used in order to decrease variance. He provides tractable
methods of variance reduction in Monte Carlo estimation of
expectations (integrals) and proves associated theoretical
results. His work has been published in
Nicola Moreni is studying variance reduction techniques for option
pricing based on Monte Carlo simulation. In particular, in a joint
project with the University of Pavia (Italy), he applies path integral
techniques to the pricing of path-dependent European options. He has
also deals with a variance reduction technique for the
Longstaff-Schwartz algorithm for American option pricing. This
technique is based on extension of the work of B. Arouna to the case
of American options.
Monte Carlo methods for American options in high dimension.L.Caramellino (University of Rome II)A.ZanetteWe have done numerical comparaison between some recent Monte Carlo algorithms
for pricing and hedging American options in high dimension, in particular
between the quantization
method of Barraquand-Martineau and an algorithm based on
Malliavin calculus
Discretization of stochastic differential equationsE.ClémentA.Kohatsu HigaD.LambertonJ.GuyonA.AlfonsiB.JourdainE.Clément, A. Kohatsu Higa and D.Lamberton develop a new approach
for the error analysis of weak convergence of the Euler scheme,
which enables them to obtain new results
on the approximation of stochastic differential equations with memory.
Their approach uses the properties of the linear equation satisfied by the error process instead of the partial differential equation derived from the Markov property of the process. It seems to be more general than the usual approach and gives results for the weak approximation of stochastic delay equations. A paper has been submitted and extensions are studied.
In his thesis, A. Kbaier develops a "statistic Romberg method" for weak approximation of stochastic differential equations. This method is especially efficient for the computation of Asian options.
J. Guyon, PhD student of B. Lapeyre and J.F. Delmas has studied how fast the Euler scheme XTn
with time-step 
t = T/n converges in law to the original random variable XT. More precisely, he has
looked for which class of functions f the approximate expectation
![Im14 ${\#120124 \mfenced o=[ c=] {f(}X_T^n{)}}$](math_image_14.png) converges to
converges to
![Im15 ${\#120124 \mfenced o=[ c=] {f(}X_T{)}}$](math_image_15.png) with speed
with speed 
t. So far, (Xt, t 0) has been a smooth
0) has been a smooth
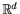 -valued diffusion.
When
-valued diffusion.
When f is smooth, it is known from D. Talay and L. Tubaro that
![Im17 ${\#120124 \mfenced o=[ c=] {f(}X_T^n{)}-\#120124 \mfenced o=[ c=] {f(}X_T{)}={C(f)\#916 t}+O\mfenced o=( c=) \#916 t^2.}$](math_image_17.png)
Using Malliavin calculus, V. Bally and D. Talay
have shown that this development remains true when f is only
mesurable and bounded, in the case when the diffusion X is uniformly hypoelliptic.
When X is uniformly elliptic, J. Guyon has extended this result to
the general class of tempered distributions. When f is a
tempered distribution, ![Im15 ${\#120124 \mfenced o=[ c=] {f(}X_T{)}}$](math_image_15.png) (resp.
(resp. ![Im14 ${\#120124 \mfenced o=[ c=] {f(}X_T^n{)}}$](math_image_14.png) ) has to be understood as
) has to be understood as
 (resp.
(resp. 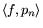 ) where
) where p
(resp. pn) is the density of XT (resp. XTn). In
particular, (f is a measurable function
with polynomial growth, a Dirac distribution or a derivative of a
Dirac distribution. The proof consists in controlling the
linear mapping 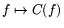 and the remainder. It can be used to
show that (
and the remainder. It can be used to
show that (f is a measurable
function with exponential growth, or when the tempered distribution
f acts on the deterministic initial value x of the diffusion X. An article is
being written, underlying applications to option pricing and hedging.
Under the supervision of Benjamin Jourdain, Aurélien Alfonsi is studying the weak and strong rates of convergence of various explicit and implicit discretization schemes for Cox-Ingersoll-Ross processes, both from a theoretical point of view and by numerical experiments.
Approximation of the invariant measure of a diffusionE.ClémentD.LambertonV.LemaireG.Pagèsinvariant measureOur work focused on the characterization of invariant measures and
on processes with jumps.
We are working on the
approximation of the invariant probability measure for SDEs with locally lipschitz coefficients and for SDEs driven by Levy processes.
We also investigate the numerical analysis
of the long run behaviour of dynamical systems (invariant measure of
diffusions, recursive learning algorithm) with F. Panloup, PhD
student of G. Pagès (see
Malliavin calculus for jump diffusionsV.BallyM.P.BavouzetM.MessaoudMalliavin calculusjump diffusionsOne of the financial numerical applications of the Malliavin calculus is the computation of the sensitivities (the Greeks) and the conditional expectations.
In the Wiener case (when the asset follows a log-normal type diffusion for example), Fournié, Lasry, Lebouchoux, Lions and Touzi have developped a methodology based on the Malliavin calculus. The main tool is an integration by parts formula which is strongly related to the Gaussian law (since the diffusion process is a functional of the Brownian motion).
In a first stage, V. Bally has worked in
collaboration with Lucia Caramellino (University Rome 2) and Antonino
Zanette (University of Udine, Italy) on pricing and hedging American
options in a local Black Scholes model driven by a Brownian motion, by
using classical Malliavin calculus
V. Bally, M.P .Bavouzet and M. Messaoud use the Malliavin calculus for Poisson processes in order to compute the Greeks (the Delta for example) of European options with underlying following a jump type diffusion. Imitating the methodology of the Wiener case, the key point is to settle, under some appropriate non-degenerency condition, an integration by parts formula for general random variables. Actually, the random variables on which the calculus is based may be the amplitudes of the jumps, the jump times and the Brownian increments.
On the one hand, M.P. Bavouzet and M. Messaoud deal with pure jump diffusion models and Merton model, where the law of the jump amplitudes has smooth density. One differentiates with respect to the amplitudes of the jumps only (pure jump diffusion) or to both jump amplitudes and Wiener increments (Merton model). Under some non-degenerency condition, one defines all the differential operators involved in the integration by parts formula.
Numerical results show that using Malliavin approach becomes extremely efficient for a discontinuous payoff. Moreover, some localization techniques may be used to reduce the variance of the Malliavin estimator. In the case of the Merton model, it is better to use the two sources of randomness, especially when there are more jumps.
On the other hand, V. Bally, MP. Bavouzet and M. Messaoud deal with pure jump diffusion models but differentiate with respect to the jump times. This case is more difficult because the law of the jump times has not smooth density, so that some border terms appear in the integration by parts formula. Thus, one introduces some weight functions in the definition of the differential operators in order to cancel these border terms. But, in this case, the non-degenerency condition is more difficult to obtain.
Another application of the Malliavin's integration by parts formula is to prove that, under appropriate hypothesis, a large variety of functionals on the Wiener space (like solutions of Stochastic Partial Differential Equations) have absolute continuous laws with smooth density. Under uniform ellipticity assumption, A. Kohatsu-Higa developped a methodology which permits to compute lower bounds of the density. Then, V. Bally relaxed this hypothesis, replacing the uniform ellipticity by only local ellipticity around a deterministic curve.
Following the work of V. Bally, M.P. Bavouzet is working on an extension of his results to jump diffusion case (driven by a Brownian motion and a Poisson process).
Lower bounds for the density of a functional V.BallyL.CaramellinoLower bounds of densityV. Bally worked on lower bounds for the density of functionals on
Wiener spaces with applications to locally elliptic diffusion
processes. V. Bally obtained a result which gave rise to a preprint
submited for publication and is working on further
developments. V. Bally and Lucia Caramellino are looking for a
lower bound for the density of the law of the portfolio value. In
collaboration with Begonia Fernandez and Ana Meda (University of Mexico), V.
Bally tries to obtain tubes evaluations for locally elliptic diffusion processes. (see
Quantization methodsG.PagèsJ.PrintemsquantizationThe quantization method applied to mathematical finance or more
generally to systems of coupled stochastic differentials equations
(Forward/Backward) as introduced in Rd). The numerical
aspects of such a method are to compute such tesselations adapted to
the underlying diffusion and to estimate theirs transition
probabilities between different cells of two successive meshes
(after a time discretization procedure). Hence, it allows the
computation of a great number of conditional expectations along the
diffusions paths.
For these reasons, such a method seems to work well with the problem
of valuation and hedging of financial products. More generally, its
applications are concerned with the American options
There exists an ``infinite dimensional'' version of
the quantization method. In particular, when a stochastic process is
viewed as an Hilbert value random variable. It is the purpose of the
functional quantization to study such quantization (see L2 framework. See [Premia]).
As concerned nonlinear filtering and quantization, let us note a
different way of study. In a work in collaboration with Bruno
Saussereau (Université de Franche-Comté, Besançon, France), we
study the filtering of nonlinear systems from a numerical point of
view: we want to compute the conditional expectations of signals when
the observation process and/or the dynamic of the signal is not linear
by means of a spectral approximation of the Zakai equation. In cite
Numerical methods for PDEs in FinanceY.Achdou (Prof. Paris 6 University)D.PommierJ.PrintemsA.Zanettesparse gridsfinite elementadaptive finite elementslattice-based methodsSparse grids methods for PDEs in Mathematical FinanceParticipants: Y.Achdou, D. Pommier, J.Printems
Sparse grids methods are special variants of the Finite Element Method and are useful when the dimension
(e.g. number of assets) increases. It relies on the approximation of functions defined on a domain of
Rd by means of special tensor products of 1-d finite elements. These special products are those for
which the indices are in the unit simplex. These methods are known to
be efficient when the solutions
are enough regular (see
A Cifre agreement on this subject between Inria and CIC is engaged involving
the PhD student David Pommier.
Adaptive finite element discretizationsParticipants: A. Zanette, A. Ern (ENPC), S. Villeneuve (Toulouse university):
We perform numerical studies on adaptive finite element discretizations for pricing and hedging European options with local volatility Black-Scholes models.
Lattice based methods for American optionsParticipants: A. Zanette (in collaboration with M.Gaudenzi, F.Pressacco and
L.Ziani):
With reference to the evaluation of the speed/precision efficiency
of pricing and hedging of American Put options, we present and
discuss numerical results in
Policy iteration algorithms for fixed point problems with nonexpansive operatorsJ.Ph.ChancelierM.MessaoudA.Sulempolicy iteration algorithmHoward algorithmdynamic programmingnonexpansive mapsThe case of Bellman equations associated to optimal control of Markov chains
on an infinite horizon with discount factor  >0 has been studied for a long time
by many authors (see e.g the monographs by Bertsekas and Puterman). Typically these equations are of the form
>0 has been studied for a long time
by many authors (see e.g the monographs by Bertsekas and Puterman). Typically these equations are of the form
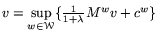 where
where
Mw is the transition matrix of the Markov chain, cw is the running utility and w is the control variable with values in some control set 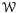 . We know that the iteration policy algorithm converges to
the solution of the Bellman equation since the
operator
. We know that the iteration policy algorithm converges to
the solution of the Bellman equation since the
operator 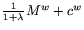 is contractive and satisfies a discrete maximum principle.
is contractive and satisfies a discrete maximum principle.
The problem addressed here concerns more general fixed point problems on a finite state space.
Typically the operator we consider is the maximum of a
contractive operator and a nonexpansive one which satisfy some appropriate properties.
Shortest path problems also lead to some fixed point problems with nonexpansive operators
but in a rather different context whereas reflecting boundaries
lead to nonexpansive operators on the boundary. This last problem appears
to be a special
case of ours.
We prove the convergence of an iteration policy algorithm and give
illustrating examples in optimal control of Markov chains in
These
results can be applied to the numerical analysis
of quasi variational inequalities (QVIs) associated to combined
impulse/stochastic optimal controls.
Stochastic control of Jump diffusionsB.Øksendal (Oslo University)A.Sulemjump diffusionsstochastic controlWe have completed a book on this subject
Anticipative stochastic optimal controlD.LefèvreinformationcontrolThe stochastic maximum principle is a powerful tool to characterize optimal control processes for a controlled system of stochastic differential equations.
Control processes represent the policy of the decision-makers and are usually assumed nonanticipative.
In this work, we waive this adaptation constraint and allow the policies to be adapted to a larger filtration that the one generated by the Brownian motion which drives the controlled stochastic differential equation. First, we show how to correctly define a unique solution for our resulting anticipative controlled system. Next, we derive a Pontryagin-type maximum principle for possibly anticipative optimal stochastic controls where the definition of the Hamiltonian is substantially modified.
Utility maximization in an insider influenced marketA.Kohatsu HigaA.Sulemantipative calculusforward integralsinsiderasymmetry informationWe study a controlled stochastic system whose state
is described by a stochastic differential equation where the
coefficients are anticipating. This setting is used to interpret
markets where insiders have some influence on the dynamics of
prices.This point of view was already partly
studied in Øksendal-Sulem
Finally, we consider a market with an
insider which influences the drift of the asset process. This last
example, which does not seem to fit into the enlargement of filtration
set-up, gives a situation where it makes a difference for a small
agent to acknowledge the existence of the insider in the market
Credit riskB.JottreauY.Elouerkhaouicredit derivativesMarshall-Olkin copulaModelisation of credit default risk has been one of the main themes of the weekly seminar in the University of Marne la Vallée. B. Jottreau has started a thesis on this subject. The next release for Premia, Premia8, will include algorithms for pricing credit risk derivatives.
Y. Elouerkhaoui has continued to work on the valuation and hedging of basket credit derivatives in the Marshall-Olkin copula framework. The two main research themes are: the modelling of default correlation in the context of credit derivatives pricing, and the study of correlation market incompleteness and hedging.
Local risk minimization hedging in multi-credit marketsWe have tackled the issue of hedging basket default swaps with their underlying single-name instruments. The payoff of basket products such as first-to-default swaps and CDOs is dependent on the multivariate default behaviour of the underlying credits. Clearly, default correlation risk introduces a market incompleteness, which cannot be hedged with plain vanilla instruments. To handle market incompleteness, we have used a local-risk minimization approach. We have highlighted the various components of the credit-hedging problem: spread risk, default risk and carry; and we have developed hedging strategies corresponding to the minimization of each type of risk.
Modelling of default correlation in complex credit derivativesWe have studied default correlation risk in a new generation of basket products, known as CDOs of CDOs (or CDO squared) and baskets of baskets. The valuation of these products depends on a compounded type of default correlation risk. Similarly to compound options, which depend on "volatility of volatility", the value of CDOs of CDOs depends on the marginal loss distributions of each underlying CDO and their joint dependence, which is referred to as "correlation of correlation".
To analyse this type of risk, we have developed the "Equivalent Single-Name Process" approximation, where the characterization of basket securities is simplified and their joint dependence is analytically tractable. We have considered each basket security in the underlying portfolio as a single-name security whose default time is driven by a Poisson process, and we have derived the properties of this process in the MO model. We have used a technique similar to our "Homogeneous Portfolio" approximation.
![]() . Here
. Here ![]()
![]() where
where ![]() is a
standard normally distributed random variable and
is a
standard normally distributed random variable and ![]() is a strictly
positive number. Note that an integration by parts formula may
be obtained just by using the usual integration by parts in the presence of the
Gaussian density. But we may go further and take
is a strictly
positive number. Note that an integration by parts formula may
be obtained just by using the usual integration by parts in the presence of the
Gaussian density. But we may go further and take ![]()
![]() where
where ![]()
![]()
![]() where
where
![]() This basic remark formula leads to efficient methods to compute by a Monte Carlo method
some irregular quantities as derivatives of option prices with
respect to some parameters (the Greeks) or conditional
expectations, which appear in the pricing of American options
by the dynamic programming).
See the papers by Fournié et al and and the papers by Bally et al, Benhamou, Bermin et al., Bernis et al., Cvitanic et al., Talay and Zheng and Temam
in .
This basic remark formula leads to efficient methods to compute by a Monte Carlo method
some irregular quantities as derivatives of option prices with
respect to some parameters (the Greeks) or conditional
expectations, which appear in the pricing of American options
by the dynamic programming).
See the papers by Fournié et al and and the papers by Bally et al, Benhamou, Bermin et al., Bernis et al., Cvitanic et al., Talay and Zheng and Temam
in .![]()
![]() is the terminal condition .
is the terminal condition .![]()
![]()
![]() which can be a function of the terminal wealth, and a
driver
which can be a function of the terminal wealth, and a
driver ![]()
![]() is the discount factor.
is the discount factor.![]()