Rewriting calculusrewritingstrategiestypesStarting from our previous works  -calculus and rewriting which we called
-calculus and rewriting which we called  -calculus
-calculus
We have proposed and studied different instances of this calculus and
their corresponding type systems. We have shown the expressive power
of this calculus by giving a simple and typed encoding of standard
strategies used in first-order rewriting. A version of the calculus
handling explicitly matching and substitution applications has been
also proposed. The explicit matching constraints have been also
extended to (a restricted class of) unification constraints allowing
one to represent, for example, infinite structures.
Explicit  -calculusHoratiuCirsteaGermainFaureClaudeKirchner
-calculusHoratiuCirsteaGermainFaureClaudeKirchnerTheoretical presentations of the  -calculus often treat matching
constraint computations as an atomic operation (although matching
constraints are explicitly expressed). Concrete implementations have
to take a much more realistic view: computations needed to find the
solutions of a matching equation (in some matching theories) can have
a strong impact on the properties of the calculus. Moreover, the
application of the obtained substitutions usually involves term
traversals.
-calculus often treat matching
constraint computations as an atomic operation (although matching
constraints are explicitly expressed). Concrete implementations have
to take a much more realistic view: computations needed to find the
solutions of a matching equation (in some matching theories) can have
a strong impact on the properties of the calculus. Moreover, the
application of the obtained substitutions usually involves term
traversals.
Following the works on explicit substitutions for  -calculus,
we propose, study and exemplify
-calculus,
we propose, study and exemplify  -calculus
with explicit constraint handling, including substitution
applications. The approach is modular and can be extended to arbitrary
matching theories. We show that the calculus is powerful enough to
deal with errors. We also prove the confluence of the calculus and the
termination of the explicit constraint handling part.
-calculus
with explicit constraint handling, including substitution
applications. The approach is modular and can be extended to arbitrary
matching theories. We show that the calculus is powerful enough to
deal with errors. We also prove the confluence of the calculus and the
termination of the explicit constraint handling part.
The explicit substitution application studied so far is not optimal
since the possible complexity of term traversals is not taken into
account. We have been working on an improved version of the calculus
that offers support for the composition of substitutions. Moreover,
the matching constraints with no solution can be eliminated earlier in
the reduction process leading to a more efficient evaluation. This can
be achieved by integrating in the explicit calculus the approach
already used for the plain calculus
Graphs in the  -calculusClaraBertolissiHoratiuCirsteaClaudeKirchner
-calculusClaraBertolissiHoratiuCirsteaClaudeKirchnerStarting from the classical untyped  -calculus and in
collaboration with Paolo Baldan from Venizia University, we have
proposed an extension with an enhanced expressive power that deals not
only with terms but also with graphs and graph transformations
-calculus and in
collaboration with Paolo Baldan from Venizia University, we have
proposed an extension with an enhanced expressive power that deals not
only with terms but also with graphs and graph transformations
The syntax of the  -calculus is adapted in order to describe
graphs and the related notions such as sharing and cycles. The
evaluation rules are also adapted for this new syntax leading to a
calculus that we call graph rewriting calculus. In this new
formalism we can represent and manipulate elaborated objects like, for
example, regular infinite entities.
-calculus is adapted in order to describe
graphs and the related notions such as sharing and cycles. The
evaluation rules are also adapted for this new syntax leading to a
calculus that we call graph rewriting calculus. In this new
formalism we can represent and manipulate elaborated objects like, for
example, regular infinite entities.
The calculus over terms is naturally generalized by using unification
constraints in addition to the standard  -calculus matching
constraints. Graph transformations are performed by explicit
application of rewrite rules as first class entities. This therefore
provides us with the basics for a natural extension of an explicit
substitution calculus to term graphs.
-calculus matching
constraints. Graph transformations are performed by explicit
application of rewrite rules as first class entities. This therefore
provides us with the basics for a natural extension of an explicit
substitution calculus to term graphs.
Typed programming with  -calculusHoratiuCirsteaClaudeKirchnerLuigiLiquoriBenjaminWack
-calculusHoratiuCirsteaClaudeKirchnerLuigiLiquoriBenjaminWackWe have extensively studied a first-order typed  -calculus à la Church called
-calculus à la Church called 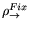 , whose type system is
mainly inspired by simply typed
, whose type system is
mainly inspired by simply typed  -calculus. The type system
enjoys subject reduction, type uniqueness and decidability of
typing. Moreover, the type system of
-calculus. The type system
enjoys subject reduction, type uniqueness and decidability of
typing. Moreover, the type system of 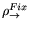 allows one to
type (object oriented flavored) fixpoints, leading to an expressive
and safe calculus. In particular, using pattern matching, one can
encode and type-check term rewrite systems in a natural and automatic
way
allows one to
type (object oriented flavored) fixpoints, leading to an expressive
and safe calculus. In particular, using pattern matching, one can
encode and type-check term rewrite systems in a natural and automatic
way
Early versions of the (untyped)  -calculus have already been used
to describe the implicit (leftmost-innermost) and user defined
strategies of ELAN
-calculus have already been used
to describe the implicit (leftmost-innermost) and user defined
strategies of ELAN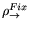 presented here refers essentially to a simpler
formulation of previously introduced versions of the rewriting
calculus
presented here refers essentially to a simpler
formulation of previously introduced versions of the rewriting
calculus
More recently, we have extended this study for two versions of a
second-order  -calculus
-calculus 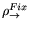 is suitable for static analysis, i.e. it
ensures that functions get arguments of the expected type. However, as
a wanted feature it does not enforce termination of typed terms: we
have shown the encoding of some interesting terms leading to infinite
reductions by the use of pattern matching features of the calculus.
is suitable for static analysis, i.e. it
ensures that functions get arguments of the expected type. However, as
a wanted feature it does not enforce termination of typed terms: we
have shown the encoding of some interesting terms leading to infinite
reductions by the use of pattern matching features of the calculus.
The consequence is that our typing discipline fits for a programming
language since we are interested in type consistency and in recursive
(potentially non-terminating) programs. Conversely, it is not adapted
for defining a logical framework, since normalization is strongly
linked to consistency, so it definitively differs from other type
systems we have proposed for the  -calculus
-calculus
As we have mentioned above, the automatic encoding we have proposed
can be done only for a restricted class of rewrite systems and only
some classical reduction strategies (e.g. outermost) have been
encoded. Therefore, we currently investigate the way this can be
generalized to unrestricted rewrite systems and to a larger class of
reduction strategies.
Typed  -calculi for logicsHoratiuCirsteaClaudeKirchnerLuigiLiquoriBenjaminWack
-calculi for logicsHoratiuCirsteaClaudeKirchnerLuigiLiquoriBenjaminWackWe are also interested in more elaborated type systems and we have
proposed a  -cube which generalizes Barendregt's
-cube which generalizes Barendregt's
 -cube. First, with Gilles Barthe and Luigi Liquori
-cube. First, with Gilles Barthe and Luigi Liquori P2TS), an algebraic extension of
Pure Type Systems. In P2TS, rewrite rules can be considered as
lambda terms with patterns, and the application of a rule is the
application of  -calculus, enhanced with matching
capabilities. This context uniformly unifies higher-order functions
and rewriting mechanisms, together with a powerful type system. Thus,
it is particularly adapted for formalizing the foundations of
programming (meta)languages and proof assistants. We have proved
various standard properties such as subject reduction and confluence.
-calculus, enhanced with matching
capabilities. This context uniformly unifies higher-order functions
and rewriting mechanisms, together with a powerful type system. Thus,
it is particularly adapted for formalizing the foundations of
programming (meta)languages and proof assistants. We have proved
various standard properties such as subject reduction and confluence.
More recently, we have proved the strong normalization for well-typed
terms P2TS into the  -calculus. For this, we rely on
an original compilation of the pattern matching capability of
-calculus. For this, we rely on
an original compilation of the pattern matching capability of P2TS
into the  -calculus. We show afterwards how to translate
types: the expressive power of System F
-calculus. We show afterwards how to translate
types: the expressive power of System F is needed in
order to fully reproduce the original typing judgments of
is needed in
order to fully reproduce the original typing judgments of P2TS. We
prove that the encoding is complete with respect to reductions and
typing, and we conclude with the strong normalization of simply-typed
P2TS terms.
We consider this work as a contribution in the study of
correspondences between rewriting and logics. In this context, we can
associate rewriting-based programs to  -terms and we are
interested in finding a suitable logic and a Curry-Howard isomorphism
between typed
-terms and we are
interested in finding a suitable logic and a Curry-Howard isomorphism
between typed  -terms and this logic.
-terms and this logic.
Models of the  -calculusGermainFaure
-calculusGermainFaureUp to now, the  -calculus has been studied only from the
perspective of its operational semantics. In collaboration with
Alexandre Miquel, we have proposed a first attempt to a Scott-style
semantics for the
-calculus has been studied only from the
perspective of its operational semantics. In collaboration with
Alexandre Miquel, we have proposed a first attempt to a Scott-style
semantics for the  -calculus, when restricted to ML-style
pattern-matching.
-calculus, when restricted to ML-style
pattern-matching.
We define a notion of  -model in the category of Scott-domains,
and prove the soundness of the reduction rules w.r.t. this notion of
-model in the category of Scott-domains,
and prove the soundness of the reduction rules w.r.t. this notion of
 -model. We then show that any universal domain
-model. We then show that any universal domain D = (D
D) with
a top element (including Scott's historical 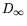 ) can be given
the structure of a
) can be given
the structure of a  -model by interpreting the structure
construction of the
-model by interpreting the structure
construction of the  -calculus by the binary sup. From this, we
deduce that the full ACI-theory of the
-calculus by the binary sup. From this, we
deduce that the full ACI-theory of the  -calculus is conservative
w.r.t. the
-calculus is conservative
w.r.t. the 
 -theory for normalizable
-theory for normalizable  -terms.
-terms.
Rule based programmingalgebraic specificationabstract data-typepattern matchingcompilationWe are studying the design and the implementation of rule based
programming languages. We are interested in modularizing our
technologies in order to make them available as separate elementary
tools.
Also, we continue our study on the application of rule based
languages. In particular, we study their applications to XML
transformations as well as the analysis and the certification of
program transformations.
Compilation of pattern-matchingJulienGuyonPierre-EtienneMoreauChristopheRingeissenIn collaboration with Marian Vittek, we have designed a new formalism,
called Tom, which allows us to integrate pattern matching facilities
into imperative languages such as C, Java or Caml. This new formalism
has been presented in
Tom does not really define a new language: it is rather a
language extension which adds new matching primitives to an existing
imperative language. From an implementation point of view, it is a
compiler which accepts different native languages: C, Java, and
Caml. The compilation process consists of translating new matching
constructs into the underlying host language. An important feature of
Tom is to support equational matching. In particular, list matching,
also known as associative matching with neutral element. Recently, we
have introduced an XML extension which allows us to manipulate XML
documents and to retrieve information via associative matching.
When developing an application which manipulates tree-like data
structures (such as symbolic computation, compilation, XML
transformation, message exchange, etc.), the need for matching can
rarely be avoided, simply because some information has to be
retrieved. Tom is particularly well suited for describing and
implementing various kinds of applications where extraction of
information has to be performed.
Representation of abstract data-typesPierre-EtienneMoreauAntoineReillesIn collaboration with Olivier Zendra from the DESIGN team, we have
studied the garbage collector algorithm provided by the standard C
implementation of the ATerm Library and stressed the fact that some
peculiarities of this functional library could be taken advantage of
by the memory management system. We have designed and implemented
GC2
In collaboration with Mark van den Brand and Jurgen Vinju of CWI at
Amsterdam, we have presented a Java back-end for ApiGen
The contribution of this work is the combination of generating a
strongly typed data-structure with maximal sub-term sharing in
Java. Practical experience shows that this approach can not only be
used for tools that are otherwise manually constructed, but also for
internal data-structures in generated tools.
Environment for rule based programmingGregoryAndrienJulienGuyonPierreHennegerStéphaneHrvatinPierre-EtienneMoreauAntoineReillesBased on the Eclipse Platform (an Integrated Development Environment),
we have developed a new plugin for Tom
In parallel to this approach, we have studied the design of a library
which allows the definition of traversal strategies. Based on
Stratego and the  -calculus, this library introduced a reduced
set of basic strategies which can be combined, via a recursion
operator
-calculus, this library introduced a reduced
set of basic strategies which can be combined, via a recursion
operator  . This results in a very flexible, efficient and easy
to use library written in Tom and Java.
. This results in a very flexible, efficient and easy
to use library written in Tom and Java.
A new parser of Tom has been reimplemented during the internships
of Pierre Henneger and Stéphane Hrvatin.
Program analysis and certification of program
transformationsClaudeKirchnerPierre-EtienneMoreauAntoineReillesWe are studying the certification of the transformation of patterns
from the Tom language into an imperative target language, like Java.
By giving a certification of the fact that the Tom compiler produces
correct target code for the Tom specification, we improve our
confidence in the Tom compiler and the rule based approach. By
giving, for each execution of the compiler a certification that the
produced code meets the specification (or a failure), we can have much
more information for debugging the compiler. It is particularly
important in the case of associative matching for example.
Our first work has been to formalize the relations between the
algebraic terms and the concrete objects representing them. Since
Tom is data-structure independent, we needed to have a formal view
of the mapping mechanism used in Tom, defining a general framework
allowing to anchor algebraic pattern-matching capabilities in existing
languages like C, Java or ML. Then, using a just enough powerful
intermediate language, which could be viewed as a subset of C
Java
ML, we formalize the behavior of compiled code and define
the correctness of compiled code with respect to pattern-matching
behavior. This allows us to prove the equivalence of compiled code
correctness with a generic first-order proposition whose proof could
be achieved via a proof assistant or an automated theorem prover. We
worked with Damien Doligiez from the Cristal project on how to connect
our tool with the Zenon theorem prover
The extension of this method to matching with theories, like
associative matching or AC-matching is not a trivial task, since there
are many new problems to solve, like proving that the matching-code
enumerates all possible matching solutions, and formalizing these
enumerations.
Rewriting, business rules and RETE networkHoratiuCirsteaClaudeKirchnerPierre-EtienneMoreauMichaelMoossenMost of business rule systems, and the Ilog Rule system in particular,
use the RETE algorithm to discriminate the rules which have to be
applied and fired. In the project, we have developed several
compilation algorithms based on the syntactic structure of the rules
(e.g.
We have proposed a new formalization of the RETE
algorithm
XML, XQuery, and rewritingHoratiuCirsteaGuillaumeDarmontClaudeKirchnerPierre-EtienneMoreauNghiem LongPhanIn order to improve the expressiveness of our tools, we have studied
the integration of XML pattern matching facilities, as well a static
typing support, into the Tom system. This has been done in the
internship of Guillaume Darmont
During the internship of Nghiem Long Phan, a comparison of XQuery and
Tom has been done. This has been followed by a work on systematic
translation from XQuery to Tom programs.
Types for XMLHoratiuCirsteaClaudeKirchnerPierre-EtienneMoreauAndersonSantanaBenjaminWackWe have contributed to the survey and analyse of the relevant existing
works on typing of rules, in particular on typing of constraint logic
programs and discuss applicability of these approaches to the
reasoning and query languages under development in the REWERSE network
of excellence such as XPathLog and Xcerpt
Manipulating and executing algebraic specificationsStéphaneHrvatinAnamariaMartins MoreiraChristopheRingeissenIn an environment of continuous and rapid evolution, software design
methodologies must incorporate techniques and tools that support
changes in software artifacts. In the FERUS project, we have developed
a tool targeted at software designers that integrates a collection of
operations on algebraic specifications written in the CASL language.
The scope of FERUS includes not only modification of existing
specifications, but also creation or derivation of new specifications,
as well as their proof and execution, which are realized through
inter-operability with existing tools. As FERUS involves the
manipulation of software specification and inter-operability with
other tools, the question of choosing appropriate representation
formats is important. In
In connection with the FERUS project, we studied how to write
structured specifications using the structuring mechanisms of CASL
and the Tom syntax for basic specifications. This study has led to the
development of a prototype to execute CASL-like structured Tom specifications. This prototype makes use of the CASL Tool Set
developed by the CoFI initiative to translate structured
specifications into basic ones. Then, Tom is used to execute basic
specifications
Rewriting and strategiesrulesstrategiesThis section considers how to extend the notion of rewriting
controlled by strategies, In particular, we continue the study of
probabilistic strategies.
Rewriting and probabilitiesOlivierBournezFlorentGarnierClaudeKirchnerIn
Using the basic probabilistic strategy operators, we modeled in ELAN 4
the protocols CSMA-CA and CSMA-CD.
We also started to work on techniques for proving almost sure
termination of a set of rewrite rules, in particular on techniques that
ensure that the mean time before termination is always finite. These
techniques are presented in the technical report
Rules and strategies for generation of chemical reactionsOlivierBournezLilianaIbănescuHélèneKirchnerLiliana Ibănescu defended her PhD thesis on ``Rule-Based Programming
and Strategies for Automated Generation of Detailed Kinetic Models for
Gas Phase Combustion of Polycyclic Hydrocarbon Molecules''
The primary objective of this thesis is to explore the approach of
using rule-based systems and strategies, for a complex problem of
chemical kinetic: the automated generation of reaction mechanisms.
The chemical reactions are naturally expressed as conditional
rewriting rules. The control of the chemical reactions chaining is
easy to describe using a strategies language, such as the one of the
ELAN system.
The thesis presents the basic concepts of the chemical kinetics, the
chemical and computational problems related to the conception and
validation of a reaction mechanism, and gives a general structure for
the generator of reaction mechanisms called GasEl. Our research
focuses on the primary mechanism generator. We give solutions for
encoding the chemical species, the reactions and their chaining, and
we present the prototype developed in ELAN. The representation of
the chemical species uses the notion of molecular graphs, encoded by a
term structure called GasEl terms. The chemical reactions are
expressed by rewriting rules on molecular graphs, encoded by a set of
conditional rewriting rules on GasEl terms. The strategies language
of the ELAN system is used to express the reactions chaining in the
primary mechanism generator. This approach is illustrated by coding
ten generic reactions of the oxidizing pyrolysis. Qualitative chemical
validations of the prototype show that our approach gives, for acyclic
molecules, the same results as the existing mechanism generators, and
for polycyclic molecules produces original results.
This thesis has been awarded by one of the INPL best PhD prices.
Rule based programming and verificationHoratiuCirsteaChandanDubeyClaudeKirchnerPierre-EtienneMoreauAntoneReillesStrategic programming
Indeed, in
Recently, in collaboration with Ozan Kahramanogullari we worked on the
calculus of structures and proposed a flexible implementation in
Tom. This allows to perform various kind of experimentations and
should help to find a good proof search strategy.
Mechanized deductiondeduction modulodecision proceduresconstrained theoriesinduction proofsequational proofscompletion proceduresterminationWe are working on integrating first-order and higher-order deduction,
calculi, decision procedures and constraint solving. We also develop
proof search procedures for program properties.
On the one hand, this year, we have designed a general
proof-theoretic setting where completion-like processes can be modeled
and studied; we have described a superposition calculus where
quantifiers are eliminated lazily. We also have studied further the
links between proof search, representation and check through the
deduction modulo and the  -calculus.
-calculus.
On the other hand, we have developed new techniques for property
proofs of rewriting with strategies, and especially, we have studied
termination of rewriting with strategies.
Size-based terminationFrédéricBlanquiIn our previous works on the termination of rewrite-based function
definitions in the Calculus of Constructions, a powerful system with
polymorphic and dependent types, we could not capture definitions with
recursive calls on non-structurally smaller arguments. Yet, since
1996, several authors (Hughes-Pareto-Sabry, Giménez, Abel, Barthe,
etc.) devised size-based termination criteria for ML-like languages
with fixpoint and case constructions allowing function definitions
with non-structurally smaller recursive calls. All these works are
based on the way inductive types are usually constructed: as fixpoints
of monotone operators on the set of terms
Certification of termination proofsFrédéricBlanquiSébastienHindererFor his master thesis, Sébastien Hinderer studied the certification of
termination proofs based on polynomial interpretations
Higher-order conditional rewritingFrédéricBlanquiClaudeKirchnerColinRibaWith the beginning of Colin's PhD in October, we started to study the
properties (confluence, termination, etc.) that are preserved when
combining conditional rewriting and  -reduction. Our ultimate
goal is to integrate in a nice and coherent way membership equational
logic and type theory. This would provide a very powerful and elegant
mechanism for defining inductive types and functions.
-reduction. Our ultimate
goal is to integrate in a nice and coherent way membership equational
logic and type theory. This would provide a very powerful and elegant
mechanism for defining inductive types and functions.
Abstract canonical presentationsRomainDemangeonClaudeKirchnerSolving goals, like deciding word problems or resolving constraints,
is much easier in some theory presentations than in others. What have
been called ``completion processes'', particularly in the study of
equational logic, involves finding appropriate presentations of a
given theory to solve easily a given class of problems.
We have designed a general proof-theoretic setting within which
completion-like processes can be modeled and studied. This framework
centers around well-founded orderings of proofs. It allows for
abstract definitions and very general characterizations of saturation
processes and redundancy criteria
Induction and rewritingClaudeKirchnerHélèneKirchnerFabriceNahonFollowing our work with Eric Deplagne on a proof theoretic framework
to perform rewrite based inductive reasonning
Inductive termination proofsOlivierFissoreIsabelleGnaedigHélèneKirchnerIn our previous work, we have proposed a new method for specifically
proving, by explicit induction, termination of rewriting under
strategies. For a given term rewriting system, we establish on the
ground term algebra that every term terminates i.e. has only finite
derivations, by supposing that any smaller term terminates. For that,
we develop proof trees representing the possible derivations from any
term using the term rewriting system. Two mechanisms are used, namely
abstraction, introducing variables that represent ground terms in
normal form and schematizes normalization of subterms the induction
hypothesis is applied on, and narrowing, schematizing rewriting of the
resulting form in different ways according to the ground instances it
represents. These two mechanisms deal with constraints used to control
the growth of the proof trees.
As it is lying on proof trees representing rewriting trees, our proof
process is also well suited for the weak termination proof, we have
focused on this year. Indeed, weak termination requires that at least
one computation branch starting from each term is finite. So we have
adapted our method to just develop branches of the proof trees, that
represent one terminating branch of the rewriting tree of any ground
term. We proceed by developing the trees in a breadth-first manner,
and by cutting redundant branches, that represent in fact different
ways of rewriting the same ground terms. Redundancy is detected in
comparying the most general unifiers of a same narrowing step in the
proof process
This is the first method for specifically establishing weak
termination of rewriting. It is of interest since rule-based programs
often do not strongly terminate, but only weakly terminate. Moreover,
in languages like ELAN, strategies exist to express that the result of
a program evaluation on a data is precisely one of its possible finite
evaluations.
The constructive aspect of our proof method, identifying and
memorizing the terminating branches in the proof trees, allows us in
addition to find a finite evaluation without fail for every term. The
second interest of this approach is then to increase the efficiency of
evaluation: performing the proof process at compile-time of a program
enables to adopt a depth-first strategy at run-time for evaluation,
avoiding by this way costly breadth-first evaluations. This work has
been realized in the context of the PRST-IL project Toundra.
A toolbox for verification and proofs of rule-based
program propertiesIsabelleGnaedigLaikaMoussaOur work on toolboxes for verification and proof of rule-based program
properties, has been continued. A new implementation of Kounalis
completeness verification procedure has been made in Tom. Lying on
pattern generation from left-hand sides of rules, and matching, it
enables to verify whether, for a given rule-based program, the
definition of the operations is complete.
A new prototype of toolbox, has been designed and implemented, to
integrate CARIBOO and the previous completeness procedure, with a
user-friendly specification editor. This work has been realized in the
context of the ACI-SI project Modulogic.
Computability and complexitycomplexitycomputabilityimplicit complexityanalog computationsWe focus on computational models working over reals with a discrete
and continuous time. Concerning discrete time models, we mainly focus
on the model of computation introduced by Blum Shub and Smale over the
reals, later on extended over arbitrary structures by Poizat. We have
obtained several syntactic characterizations of complexity classes in
this model. These characterizations subsume classical ones when
restricted to booleans. Concerning continuous time models, we have
provided a machine independent characterization of elementary
computable functions over reals that extends the characterization
obtained by Campagnolo. The previous known characterization was
restricted to functions over the reals preserving integers.We also
shown that it is possible to build a minimization schema in order to
get a characterization of all (non-necessarily elementary) computable
functions preserving integers.
Complexity in the Blum, Shub, Smale model of computationOlivierBournezPaulinJacobé de NauroisIn order to model discrete time computation over real numbers, Blum,
Shub and Smale have introduced in 1989 a new model of computation,
referred as BSS machine or sometimes real Turing machine. In this
model, the complexity of a computational problem is given by the
number of elementary arithmetical operations and comparisons needed to
solve this problem, independently of the underlying representation of
real numbers. This makes it very different from the recursive analysis
model, and occurs to be a very natural way to describe computational
problems over real numbers. The BSS model of computation has been
later on extended to the notion of computation over arbitrary logical
structure. Since classical complexity theory occurs to be the
restriction of this general model to boolean structures, it gives a
new insight on previous questions on classical complexity theory and
its links with logic.
Paulin de Naurois' PhD thesis, jointly supervised by Olivier Bournez,
Jean-Yves Marion (Calligramme research team) and Felipe Cucker (Hong
Kong City University), is focused on studying complexity in this
model. It has been defended on 15th of December, 2004
In this thesis, we have provided new completeness results for
geometrical problems when the arbitrary structure is specialized to
the set of real numbers with addition and order. The range of these
completeness results covers many of the most important complexity
classes over this setting, which is one of the three major ones for
complexity theory over arbitrary structures.
We also provided several machine independent characterizations of
complexity classes over arbitrary structures. We extended some results
by Grädel, Gurevich and Meer in descriptive complexity,
characterizing deterministic and non deterministic polynomial time
decision problems in terms of logics over meta-finite structures. We
extended some results in implicit complexity by Bellantoni and
Cook
Analog computationsOlivierBournezEmmanuelHainryThere are many ways to model analog computers. Unifying those models
would therefore be a crucial matter as opposed to the discrete case,
there is no property stating that those models are equivalent. It is
possible to distinguish two groups in those models: on one side,
continuous time models; on the other side, discrete time models
working on continuous structures as a model derived from Turing
machines. The first group contains in particular some sets of
functions defined by Moore in
There are few comparisons between classes of functions from the first
group and from the second group, and in particular, there were almost
no result of equality.
In
We generalized this result to all higher levels of the Grzegorczyk
Hierarchy.
Concerning recursive analysis, our results provide
machine-independent characterizations of natural classes of computable
functions over the real numbers, allowing to define these classes
without usual considerations on higher-order (type 2) Turing
machines. Concerning analog models, our results provide a
characterization of the power of a natural class of analog models over
the real numbers.
In
In some sense, the problem we solve there is the definition of a
minimization operator, which is strong enough to get at least Turing
machine power, but not too strong to get the technical problems of
![]() -calculus and
rewriting that we called
-calculus and
rewriting that we called ![]() -calculus . We have been studying the
expressiveness of this general formalism and the properties of its
various instances.
-calculus . We have been studying the
expressiveness of this general formalism and the properties of its
various instances.![]() -calculus, and more generally in rewrite engines.
-calculus, and more generally in rewrite engines.