Overall Objectives
Overall Objectives
hidden Markov model (HMM)
particle filtering
risk evaluation
localisation
navigation and tracking
rare event simulation
The scientific objectives of ASPI are the design, analysis and implementation of interacting Monte Carlo methods, also known as particle methods, with focus on
statistical inference in hidden Markov models, e.g. state or parameter estimation, including particle filtering,
risk evaluation, including simulation of rare events.
The whole problematic is multidisciplinary, not only because of the many scientific and engineering areas in which particle methods are used, but also because of the diversity of the scientific communities which have already contributed to establish the foundations of the field :
target tracking, interacting particle systems, empirical processes, genetic algorithms (GA), hidden Markov models and nonlinear filtering, Bayesian statistics, Markov chain Monte Carlo (MCMC) methods, etc. Intuitively speaking, interacting Monte Carlo methods are sequential simulation
methods, in which particles
explorethe state space by mimicking the evolution of an underlying random process,
learnthe environment by evaluating a fitness function,
and
interactso that only the most successful particles (in view of the value of the fitness function) are allowed to survive and to get offsprings at the next generation.
The effect of this mutation / selection mechanism is to automatically concentrate particles (i.e. the available computing power) in regions of interest of the state space. In the special case of particle filtering, which has numerous applications under the generic heading of
positioning, navigation and tracking, in target tracking, computer vision, mobile robotics, ubiquitous computing and ambient intelligence, sensor networks, etc. each particle represents a possible hidden state, and is multiplied or terminated at the next generation on the basis of its
consistency with the current observation, as quantified by the likelihood function. These genetic–type algorithms are particularly adapted to situations which combine a prior model of the mobile displacement, sensor-based measurements, and a base of reference measurements, for example in the
form of a digital map (digital elevation map, attenuation map, etc.). In the most general case, particle methods provide approximations of probability distributions associated with a Feynman–Kac flow, by means of the weighted empirical probability distribution associated with an interacting
particle system, with applications that go far beyond filtering, in simulation of rare events, simulation of conditioned or constrained random variables, molecular simulation, etc.
ASPI essentially carries methodological research activities, rather than activities oriented towards a single application area, with the objective of obtaining generic results with high potential for applications, and of bringing these results (and other results found in the literature)
until implementation on a few appropriate examples, through collaboration with industrial partners.
The main applications currently considered are geolocalisation and tracking of mobile terminals, calibration of models for electricity price, and risk assessment for complex hybrid systems such as those used in air traffic management.
Scientific Foundations
Monte Carlo methods
Monte Carlo methods are numerical methods that are widely used in situations where (i) a stochastic (usually Markovian) model is given for some underlying process, and (ii) some quantity of interest should be evaluated, that can be expressed in terms of the expected value of a
functional of the process trajectory, or the probability that a given event has occurred. Numerous examples can be found, e.g. in financial engineering (pricing of options and derivative securities)
Nof the sample goes to infinity, with rate
 and the asymptotic variance can be estimated using an appropriate central limit theorem. To reduce the asymptotic variance of the estimator, many variance reduction techniques have been proposed. However, running independent Monte Carlo simulations can lead to very poor results,
because trajectories are generated
blindly, and only afterwards are the corresponding weights evaluated, which can happen to be negligible in which case the corresponding trajectory is not going to contribute to the estimator, i.e. computing power has been wasted.
and the asymptotic variance can be estimated using an appropriate central limit theorem. To reduce the asymptotic variance of the estimator, many variance reduction techniques have been proposed. However, running independent Monte Carlo simulations can lead to very poor results,
because trajectories are generated
blindly, and only afterwards are the corresponding weights evaluated, which can happen to be negligible in which case the corresponding trajectory is not going to contribute to the estimator, i.e. computing power has been wasted.
A recent and major breakthrough, a brief mathematical presentation of which is given in
explorethe state space under the effect of a
mutationmechanism which mimics the evolution of the underlying process,
and are
replicatedor
terminated, under the effect of a
selectionmechanism which automatically concentrates the particles, i.e. the available computing power, into regions of interest of the state space.
In full generality, the underlying process is a Markov chain, whose state space can be finite, continuous (Euclidean), hybrid (continuous / discrete), graphical, constrained, time varying, pathwise, etc., the only condition being that it can easily be
simulated. The very important case of a sampled continuous–time Markov process, e.g. the solution of a stochastic differential equation driven by a Wiener process or a more general Lévy process, is also covered.
In the special case of particle filtering, originally developed within the tracking community, the algorithms yield a numerical approximation of the optimal filter, i.e. of the conditional probability distribution of the hidden state given the past observations, as a (possibly weighted)
empirical probability distribution of the system of particles. In its simplest version, introduced in several different scientific communities under the name of
interacting particle filter
Particle methods are currently being used in many scientific and engineering areas : positioning, navigation, and tracking
Particle methods are very easy to implement, since it is sufficient in principle to simulate independent trajectories of the underlying process. The whole problematic is multidisciplinary, not only because of the already mentioned diversity of the scientific and engineering areas in which
particle methods are used, but also because of the diversity of the scientific communities which have contributed to establish the foundations of the field : target tracking, interacting particle systems, empirical processes, genetic algorithms (GA), hidden Markov models and nonlinear
filtering, Bayesian statistics, Markov chain Monte Carlo (MCMC) methods.
General framework : Particle approximations of Feynman–Kac flows
The following abstract point of view, developed and extensively studied by Pierre Del Moral
![Im2 ${\#9001 \#956 _n,f\#9002 =\mfrac {\#9001 \#947 _n,f\#9002 }{\#9001 \#947 _n,1\#9002 }~{\mtext where}~\#9001 \#947 _n,f\#9002 ={\#120124 [f(}X_n{)~}\#8719 _{k=0}^ng_k{(}X_k{)]~,}}$](math_image_2.png)
where
Xndenotes a Markov chain with (possibly) time dependent state spaces
Enand with transition kernels
Qn, and where the nonnegative potential functions
gnplay the role of selection functions. Feynman–Kac flows (FK) naturally arise whenever importance sampling is used, as seen from (IS) above : this applies for instance to simulation of rare events, to filtering, i.e. to state estimation in hidden Markov models (HMM), etc.
Clearly, the unnormalized linear flow satisfies the dynamical system

with the nonnegative kernel
 , and the associated normalized nonlinear flow of probability distributions satisfies the dynamical system
, and the associated normalized nonlinear flow of probability distributions satisfies the dynamical system

which can be decomposed in the following two steps

Conversely, the normalizing constant
 , hence the unnormalized (linear) flow as well, can be expressed in terms of the normalized (nonlinear) flow : indeed
, hence the unnormalized (linear) flow as well, can be expressed in terms of the normalized (nonlinear) flow : indeed
 . To solve these equations
numerically, and in view of the basic assumption that it is easy to
simulater.v.'s according to the probability distributions
. To solve these equations
numerically, and in view of the basic assumption that it is easy to
simulater.v.'s according to the probability distributions
 , i.e. to mimic the evolution of the Markov chain, the original idea behind particle methods consists of looking for an approximation of the probability distribution
, i.e. to mimic the evolution of the Markov chain, the original idea behind particle methods consists of looking for an approximation of the probability distribution
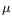
nin the form of a (possibly weighted) empirical probability distribution associated with a system of particles :

The approximation is completely characterized by the set
 of particle positions and weights, and the algorithm is completely described by the mechanism which builds
of particle positions and weights, and the algorithm is completely described by the mechanism which builds

kfrom

k-1. In practice, in the simplest version of the algorithm, known as the
bootstrapalgorithm, particles
are selected according to their respective weights (selection step),
move according to the Markov kernel
Qk(mutation step),
are weighted by evaluating the fitness function
gk(weighting step).
The algorithm yields a numerical approximation of the probability distribution
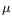
nas the weighted empirical probability distribution
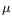
nNassociated with a system of particles, and many asymptotic results have been proved as the number
Nof particles (sample size) goes to infinity, using techniques coming from applied probability (interacting particle systems, empirical processes
 , convergence as empirical processes indexed by classes of functions, uniform convergence in time (see also
, convergence as empirical processes indexed by classes of functions, uniform convergence in time (see also
in the redistribution step, sampling with replacement could be replaced with other redistribution schemes so as to reduce the variance (this issue has also been addressed in genetic algorithms),
to reduce the variance and to save computational effort, it is often a good idea not to redistribute the particles at each time step, but only when the weights
 are too much uneven.
are too much uneven.
Most of the results proved in the literature assume that particles are redistributed (i) at each time step, and (ii) using sampling with replacement. Studying systematically the impact of these algorithmic variations on the convergence results is still to be done. Even with
interacting Monte Carlo methods, it could happen that some particle
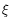
kigenerated in one time step has a negligible weight
gk(
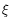
ki) : if this happens for too many particles in the sample
 , then computer power has been wasted, and it has been suggested to use importance sampling again in the mutation step, i.e. to let particles explore the state space under the action of an alternate wrong mutation kernel, and to weight the particles according to their likelihood for
the true model, so as to compensate for the wrong modeling. More specifically, using an arbitrary importance decomposition
, then computer power has been wasted, and it has been suggested to use importance sampling again in the mutation step, i.e. to let particles explore the state space under the action of an alternate wrong mutation kernel, and to weight the particles according to their likelihood for
the true model, so as to compensate for the wrong modeling. More specifically, using an arbitrary importance decomposition

results in the following general algorithm, known as the
sampling with importance resampling(SIR) algorithm, in which particles
are selected according to their respective weights (selection step),
move according to the importance Markov kernel
Pk(mutation step),
are weighted by evaluating the importance weight function
Wkon the resulting transition (weighting step).
Statistics of HMM
hidden Markov model (HMM)
asymptotic statistics
local asymptotic normality (LAN)
exponential forgetting
exponential stability
Hidden Markov models (HMM) form a special case of partially observed stochastic dynamical systems, in which the state of a Markov process (in discrete or continuous time, with finite or continuous state space) should be estimated from noisy observations. The conditional probability
distribution of the hidden state given past observations is a well–known example of a normalized (nonlinear) Feynman–Kac flow, see
Beyond the recursive estimation of an hidden state from noisy observations, the problem arises of statistical inference of HMM with general state space, including estimation of model parameters, early monitoring and diagnosis of small changes in model parameters, etc.
Large time asymptotics A fruitful approach is the asymptotic study, when the observation time increases to infinity, of an extended Markov chain, whose state includes (i) the hidden state, (ii) the observation, (iii) the prediction filter (i.e. the
conditional probability distribution of the hidden state given observations at all previous time instants), and possibly (iv) the derivative of the prediction filter with respect to the parameter. Indeed, it is easy to express the log–likelihood function, the conditional least–squares
criterion, and many other clasical contrast processes, as well as their derivatives with respect to the parameter, as additive functionals of the extended Markov chain.
The following general approach has been proposed :
first, prove an exponential stability property (i.e. an exponential forgetting property of the initial condition) of the prediction filter and its derivative, for a misspecified model,
from this, deduce a geometric ergodicity property and the existence of a unique invariant probability distribution for the extended Markov chain, hence a law of large numbers and a central limit theorem for a large class of contrast processes and their derivatives, and a local
asymptotic normality property,
finally, obtain the consistency (i.e. the convergence to the set of minima of the associated contrast function), and the asymptotic normality of a large class of minimum contrast estimators.
This programme has been completed in the case of a finite state space
Small noise asymptotics Another asymptotic approach can also be used, where it is rather easy to obtain interesting explicit results, in terms close to the language of nonlinear deterministic control theory
The following results have been obtained using this approach :
the consistency of the maximum likelihood estimator (i.e. the convergence to the set
Mof global minima of the Kullback–Leibler divergence), has been obtained using large deviations techniques, with an analytical approach
if the abovementioned set
Mdoes not reduce to the true parameter value, i.e. if the model is not identifiable, it is still possible to describe precisely the asymptotic behavior of the estimators
rof the Fisher information matrix
 is constant in a neighborhood of the set
is constant in a neighborhood of the set
M, then this set is a differentiable submanifold of codimension
r, (ii) the posterior probability distribution of the parameter converges to a random probability distribution in the limit, supported by the manifold
M, absolutely continuous w.r.t. the Lebesgue measure on
M, with an explicit expression for the density, and (iii) the posterior probability distribution of the suitably normalized difference between the parameter and its projection on the manifold
M, converges to a mixture of Gaussian probability distributions on the normal spaces to the manifold
M, which generalized the usual asymptotic normality property,
it has been shown in
 , in terms of the Kalman filter associated with the linear tangent linear Gaussian model, and (ii) the score function (i.e. the derivative of the log–likelihood function w.r.t. the parameter), evaluated at the true value of the parameter and suitably normalized, converges to a
Gaussian r.v. with zero mean and covariance matrix
, in terms of the Kalman filter associated with the linear tangent linear Gaussian model, and (ii) the score function (i.e. the derivative of the log–likelihood function w.r.t. the parameter), evaluated at the true value of the parameter and suitably normalized, converges to a
Gaussian r.v. with zero mean and covariance matrix
 .
.
New Results
Adaptive splitting for rare event analysis
Frédéric
Cérou
Pierre
Del Moral
Arnaud
Guyader
Hélène
Topart
rare event
multilevel splitting
asymptotic normality
quantile
The estimation of rare event probabilities is a crucial issue in areas such as reliability, telecommunication networks, air traffic management, etc. In complex systems, analytical methods cannot be used, and naive Monte Carlo methods are clearly unefficient to estimate accurately
probabilities of order less than
10
-9, say. Besides importance sampling, a widespread technique is multilevel splitting, which requires at least some knowledge of the system, to decide where to place the intermediate level sets. This is not always possible, and an adaptive algorithm has been proposed to cope
with this problem, and has been analyzed thoroughly in the one–dimensional case.
To be specific, let
 denote a strong Markov process with values in
denote a strong Markov process with values in
 and with continuous trajectories. Assume that the origin is a recurrent set in the sense that the hitting time
and with continuous trajectories. Assume that the origin is a recurrent set in the sense that the hitting time
T
0
t
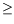
X
t
has finite expectation. The problem is to estimate the probability
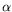 that the process reaches the level
that the process reaches the level
 before returning to the origin, i.e. before time
before returning to the origin, i.e. before time
T0, starting from the deterministic initial condition
0<
X
0=
x
0<
M.
The proposed algorithm is described as follows : At generation
l= 1 :
independently for
 , let the excursion
, let the excursion
 be simulated until
be simulated until
T0j= inf{
t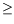 0 :
0 :
Xtj= 0}, according to the Markov kernel of
Xand starting from the deterministic initial condition
X0j=
x0, and let

denote the maximum of the excursion
Xj, i.e. the closest point to the level
M,
sort the sample
 in increasing order
in increasing order

let
 play the role of the (virtual) level at the generation 1, and keep unchanged the
play the role of the (virtual) level at the generation 1, and keep unchanged the
kexcursions approaching the level
Mmost closely, i.e. let
Sn,
j2=
Sn, (
j)1for any
 .
.
At generation
l :
independently for
 , let the excursion
, let the excursion
 be simulated until
be simulated until
T0j= inf{
t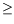 0 :
0 :
Xtj= 0}, according to the Markov kernel of
Xand starting from the initial condition
 , and let
, and let

denote the maximum of the excursion
Xj, i.e. the closest point to the level
M,
sort the sample
 in increasing order
in increasing order

let
 play the role of the (virtual) level at the generation
play the role of the (virtual) level at the generation
l, and keep unchanged the
kexcursions approaching the level
Mmost closely, i.e. let
Sn,
jl+ 1=
Sn, (
j)lfor any
 .
.
At each generation
l, the
kexcursions approaching the level
Mmost closely are kept unchanged, i.e. the fraction of those excursions which reach the (virtual) level
 is
is
 exactly, and
(
exactly, and
(
n-
k)new excursions are simulated, starting from the current (virtual) level
 . The algorithm continues until generation
. The algorithm continues until generation
l=
Lwhere the current (virtual) level
 exceeds the level
exceeds the level
M, i.e.
Ldenotes the first generation where at least one excursion reaches the level
M : let
kL+ 1denote the exact number of such excursions, i.e. the number of elements in the sample
 that exceed the level
that exceed the level
M. Then, the rare event probability is estimated as

and the number of (virtual) intermediate levels is
L.
In this one–dimensional framework, almost sure convergence and asymptotic normality of the estimator has been proved, with the same variance as other algorithms that use given intermediate levels. It has also been showed on numerical examples that this method can be used for
multidimensional problems as well, even if there is still no convergence result in this case.
Particle filter without likelihood
Vivien
Rossi
François
Le Gland
kernel method
regularization
It is commonly assumed that implementing particle filter algorithms requires being able to
simulate independent realizations of the hidden state,
and evaluate a likelihood function, which quantifies the consistency of each simulated state with the current observation.
It is possible however to get rid of this assumption, using kernel–based regularization methods that have already been considered in
jointly simulate independent realizations of the hidden state and the observation,
and validate each simulated pair (hidden state, observation) against the current observation.
If a binary validation rule is used, it may very well happen that all the simulated pairs are rejected, in which case the sequential particle algorithm introduced in
no explicit expression is available for the likelihood function,
there is no likelihood function (for instance because the observation noise does not appear in an additive way),
there is no noise on (some components of) the observation, which can be interpreted as a posterior constraint on the hidden state, etc.
Preliminary results have been obtained by Vivien Rossi in his PhD thesis
Particle approximations of Feynman–Kac flows depending on a parameter
Natacha
Caylus
François
Le Gland
hidden Markov model (HMM)
Monte Carlo maximum likelihood (MCML)
This is a collaboration with Nadia Oudjane, from the OSIRIS (Optimisation, simulation, risque et statistiques) department of Électricité de France R&D, see
In full generality, given nonnegative kernels
Rnand a nonnegative measure
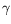 0, we consider the unnormalized (linear) Feynman–Kac flow
0, we consider the unnormalized (linear) Feynman–Kac flow

A well–known example is provided by the unnormalized conditional probability distribution of the hidden state given past observations, when the hidden state and the observation form jointly a Markov chain : this includes HMM and switching AR models as special cases,
with the decomposition
 where
where
Qkis the Markov transition kernel and where the selection function
gkis the likelihood function.
If the nonnegative kernels depends smoothly (continuously or differentiably) on a parameter, in such a way that the Feynman–Kac flow depends smoothly on the parameter, we would like to design a particle approximation to would depend smoothly on the parameter as well. The need for such a
regularity property arises for instance
in sensitivity analysis, e.g. in the computation of Greeks, in option pricing,
in statistics of HMM, see
The smooth particle approximation introduced last year has been further studied, where a unique interacting particle system is propagated for a given (pivot) value of the parameter, and where secondary weights are computed separately for each value of the parameter in a neighborhood of the
pivot value. Differentiating these secondary weights w.r.t. the parameter yields a particle approximation of the linear tangent Feynman–Kac flow, which coincides with an earlier approach followed in the team, where a particle approximation is derived direxctly from the equation satisfied by
the linear tangent Feynman–Kac flow. The new results obtained this year for the joint particle approximation of the Feynman–Kac flow and the linear tangent Feynman–Kac flow are
a central limit theorem,
uniform estimates over a neighborhood of the pivot value of the parameter.
Recursive maximum likelihood estimation for structural health monitoring : tangent filter implementations
Fabien
Campillo
linear tangent filter
maximum likelihood estimation
recursive estimation
structural health monitoring
Tracking varying parameters using likelihood–based recursive algorithms has been shown to adapt well to parameter change on a sample–wise level. The objective of the current work is to extend previous work on high order models from realistic civil aeronautic structures. This work is
jointly done with Laurent Mevel from SISTHEM project–team. Work has progressed utilizing Kalman based recursive estimation algorithms and it has been shown that these kind of algorithms can be computed effectively using particular filtering techniques
The implementation and simulation studies have been handled by Nimish Sharmah during his internship, under the joint supervision of Laurent Mevel and Fabien Campillo. The work has focused on the evaluation of finding the best parameterization between the complex poles and the
frequency/damping coefficients. It has been shown by Monte Carlo studies that the pole estimation is much simpler than finding good estimates for the damping, even if the parameterizations seem to be a priori equal. Monte Carlo studies have shown that the confidence intervals on damping
coefficients can be quite high even if the corresponding poles are well estimated.
Bayesian methods for natural resources management
Fabien
Campillo
Vivien
Rossi
Rivo
Rakotozafy
Bayesian estimation
Markov chain Monte Carlo (MCMC)
Metropolis–Hastings
natural resource management
Markov chain Monte Carlo (MCMC) methods are now widely used to study the evolution of natural resources, such as biomass in fisheries or the dynamics of forests. Although flexible, these methods have however low convergence speeds. By contrast, particle filtering methods are fast but are
not well adapted to these models, where measurements are sampled daily, monthly or yearly. Therefore there is no need to treat these measurements in a recursive way, and it seems more appropriate to call upon Monte Carlo methods in interaction, such as population Monte Carlo
In the first case study particle filtering has been applied to calibrate tree–growth models, which are complex and highly nonlinear. MCMC (Metropolis–Hastings) techniques have been compared with particle filtering methods for fitting and identifying such model. The first results showed
that MCMC methods are more consuming in terms of computational time. By comparison, particle filtering is faster and less sensitive to prior knowledge, but it also presents a greater variance than the MCMC methods.
This is a collaboration with Cédric Gaucherel, from CEREVE (centre européen de recherche et d'enseignement de géosciences de l'environnement, in Aix–en–Provence), Étienne Rivot (Agrocampus de Rennes) and Rivo Rakotozafy (University of Fianarantsao, in visit within ASPI).
Nearest neighbor classification in infinite dimension
Frédéric
Cérou
Arnaud
Guyader
classification
consistency
non parametric statistics
Given an
n–sample
 of training data, where the 0-1 valued random variable
of training data, where the 0-1 valued random variable
Yiis the class, or label, of the random element
Xiwith values in the metric space
 , the problem of classification is to predict the label
, the problem of classification is to predict the label
Yof a new random element
X. The joint probability distribution of
(
X,
Y)on
 is characterized by
is characterized by
the probability distribution
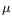 (
(
dx)of
Xon
 ,
,
and by the
regressionfunction defined by
![Im44 ${\#951 (x)=\#8473 [Y=1\#8739 X=x]}$](math_image_44.png) for any
for any
xin
 .
.
It is easy to prove that the Bayes classifier

minimizes the probability of error over all 0-1 valued classifiers
gndefined on
 , i.e.
, i.e.
![Im46 ${{\#8473 [}g_n{(X)\#8800 Y]\#8805 }L^*~where~L^*{=\#8473 [}g^*{(X)\#8800 Y]~,}}$](math_image_46.png)
is the Bayes probability of error, or Bayes risk.
The
k-nearest neighbor classifier
gnconsists in the simple following rule : look at the
knearest neighbors of
Xin the
n–sample, and choose 0 or 1 for its label according to the majority rule. In the case where
 , this classifier is universally consistent
, this classifier is universally consistent
ngoes to infinity, whatever the joint probability distribution of
(
X,
Y), provided that
k/
ngoes to 0. Unfortunately, this result is no longer valid in general metric spaces, and the objective is to find out reasonable sufficient conditions for the weak consistency to hold. Even in finite dimension, there are exotic distances such that the nearest neighbor
does not even gets closer (in the sense of the distance) to the point of interest, and the state space
 needs to be complete for the metric
needs to be complete for the metric
d, which is the first condition. Some regularity on
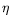 is required next : clearly continuity is too strong because it is not required in finite dimension, and a weaker form of regularity is assumed.
is required next : clearly continuity is too strong because it is not required in finite dimension, and a weaker form of regularity is assumed.
The following consistency result has been obtained
 is separable and if the following
Besicovich condition
is separable and if the following
Besicovich condition

holds for every
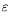 >0as
>0as
 , or equivalently if
, or equivalently if

in probability as
 , where
, where
 denotes the closed ball of radius
denotes the closed ball of radius
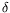 centered at
centered at
x, then the nearest neighbor classifier is weakly consistent, i.e.
![Im52 ${{\#8473 [}g_n{(X)\#8800 Y]\#8594 }L^*~,}$](math_image_52.png)
as
 . Note that the Besicovich condition is always fulfilled in finite dimensional vector spaces (this result is called the Besicovich theorem), and that a counterexample can be given
. Note that the Besicovich condition is always fulfilled in finite dimensional vector spaces (this result is called the Besicovich theorem), and that a counterexample can be given
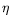 .
.
Contracts and Grants with Industry
Conditional Monte Carlo methods for risk assessment — IST project HYBRIDGE
Frédéric
Cérou
François
Le Gland
Contract INRIA 1 02 C 0037 — January 2002/April 2005
In view of the undergoing evolution in management and control of large complex real–time systems towards an increasing distribution of sensors, decisions, etc., and an increasing concern for safety criticality, the IST project HYBRIDGE addresses methodological issues in stochastic analysis
and distributed control of hybrid systems, with conflict management in air trafic as its target application area. It is coordinated by National Aerospace Laboratory (NLR, Netherlands) and its partners are Cambridge University (United Kingdom), Universita di Brescia and Universita dell'Aquila
(Italy), Twente University (Netherlands), National Technical University of Athens (NTUA, Greece), Centre d'Études de la Navigation Aérienne (CENA), Eurocontrol Experimental Center (EEC), AEA Technology and BAe Systems (United Kingdom), and INRIA.
The contribution of ASPI to this project concerns the work package on modeling accident risks with hybrid stochastic systems, and the workpackage on risk decomposition and risk assessment methods, and their implementation using conditional Monte Carlo methods
Calibration of models for electricity spot and futures price — contract with EDF
François
Le Gland
See
Contract INRIA 1 04 C 0862 — October 2004/September 2005
This is a collaboration with Nadia Oudjane, from the OSIRIS (Optimisation, simulation, risque et statistiques) department of Électricité de France R&D.
The objective is to estimate parameters in various multi–factor models for electricity spot price, from the observation of futures contracts prices that are traded in the market. This problems fits within the general framework of parameter estimation in hidden Markov models, and we propose
to rely on joint particle approximation schemes for the optimal filter and the linear tangent filter, so as to maximize the likelihood function, or other suitable contrast functions, w.r.t. the parameters. In the simple case where the futures contracts are written for electricity delivery
over a single period of time, and if multi–factor models are based on Ornstein–Uhlenbeck processes driven by a Brownian motion, then the problem is linear Gaussian and explicit expressions provided by the Kalman filter can be used to assess the performance of the proposed approach. In
practice however futures contracts are usually written for electricity delivery over a long period of time, and realistic multi–factor models should be used, based on Ornstein–Uhlenbeck processes driven by a Lévy process, which make the problem non–linear with non Gaussian noise
structure.
A two factor model proposed by the industrial partner, with a long–term factor modeled as a Brownian motion with drift and a short–term factor modeled as an Ornstein–Uhlenbeck process driven by an independent Brownian motion, has been considered first. It appears that the log–price of a
future contract for delivery over a multiple of the unit delivery period, depends linearly on the long–term factor, and a Rao–Blackwellized form has been derived for the particle approximation of the likelihood function. To locate the global maxima of the likelihood function, particle methods
over the parameter space, such as annealed Feynman–Kac models
Localization and tracking of mobile terminals — contract with FTRD
Fabien
Campillo
Frédéric
Cérou
François
Le Gland
Julien
Guillet
See
Contract ...— May 2005/April 2006
The objective is to implement and assess the performance of particle filtering in localisation and tracking of mobile terminals in a wireless network, using network measurements (received power level and possibly TDOA (time difference of arrival)) and a database of reference measurements
of the power level, available in a few points or in the form of a digital map (power attenuation map). Generic algorithms will be proposed and specialized to the indoor context (wireless local area network, e.g. WiFi) and to the outdoor context (cellular network, e.g. GSM) when necessary.
Constraints and obstacles such as building walls in an indoor environment, street, road or railway networks in an outdoor environment, will be represented in a simplified manner, using a prior model on a graph, e.g. a Voronoï graph as in similar experiments in mobile robotics
Dissemination
Scientific animation
F. Campillo has reported on the PhD thesis of David Bourgeois (ONERA and université de Cergy-Pontoise, advisors : Marc Flécheux and Inbar Fijalkow). He is a member of the committee for the PhD thesis of Thomas Bréhard (université de Rennes 1 and IRISA, advisor :
Jean–Pierre Le Cadre). He is a member of the «conseil de laboratoire» of IRISA (UMR 6074) and of the «conseil de l'école doctorale de physique, modélisation et sciences pour l'ingénieur de Marseille». He is the INRIA representative for scientific relations with Madagascar, within
the SARIMA (support to research activities in computer science and mathematics in Africa) project supported by INRIA and MAE (ministère des affaires étrangères). In relation with this activity, he has spent one week in Antananarivo in August 2005.
F. Le Gland has reported on the PhD thesis of Karim Dahia (ONERA and université Joseph Fourier, advisors : Christian Musso and Dinh–Tuan Pham) and Afef Sellami (université Paris–Dauphine, advisors : Gilles Pagès and Huyên Pham). He is a member of the committe for the
HDR (habilitation à diriger les recherches) of James Ledoux (université de Rennes 1) and of Bruno Tuffin (université de Rennes 1).
A. Guyader and F. Le Gland are members of the «commission de spécialistes» in applied mathematics (section 26) of université de Rennes 2.
V. Rossi assembled the research project MIP (Modélisation Intégrée en Dynamique des Populations : Applications à la Gestion et à la Conservation) in partnership with the Centre d'Écologie Fonctionnelle et Évolutive, UMR CNRS 5175 and the UMR ENSAM-INRA Analyse des Systèmes et
Biométrie. The main objective is to use Bayesian statistics to circumvent problems generally encountered in population dynamics models. The project funds are grants of the région Languedoc–Roussillon.
Teaching
F. Campillo gives a course on Markov models, hidden Markov models, filtering and particle filtering at université de Sud Toulon–Var, within the Master «Mathématiques (Filtrage et traitement des données)» and the Master «Sciences et Technologies (Sciences de la mer, environnement,
systèmes)».
F. Le Gland gives a course on Kalman filtering, particle filtering and hidden Markov models, at université de Rennes 1, within the Master STI (école doctorale MATISSE), a course on Bayesian filtering and particle approximation, at ENSTA, Paris, within the quantitative
finance track, and a course on hidden Markov models, at ENST Bretagne, Brest.
Participation in workshops, seminars, lectures, etc.
In addition to presentations with a publication in the proceedings, and which are listed at the end of the document, members of ASPI have also given the following presentations.
F. Campillo has given a talk on particle filters and sequential data assimilation at the ARC ADOQA (Data assimilation for air quality) meeting at ENPC (Marne–la–Vallée) in June 2005.
A. Guyader has given a talk on nearest neighbor classification in infinite dimension at the seminar ENSA-M/INRA/UM 2 in Montpellier in January 2005, and at the «Rencontre de Statistiques Mathématiques» at CIRM in Marseilles in December 2005. He has also given a talk on adaptive
multilevel splitting for rare event analysis at the «Journées STAR» in Rennes in November 2005. He has organized with Magalie Fromont and Éric Matzner-Løber the «Journées de Statistique et Applications en Biologie» at université de Rennes 2 in September 2005.
F. Le Gland has given a talk on statistical inference of HMM using Monte Carlo methods with interaction, at the 5th workshop on Statistical Inference for Continuous Time Stochastic Processes, organized by Yurii Kutoyants in Le Mans in January 2005, and at the «Journées
STAR» in Rennes in November 2005. He has given several talks on a sequential particle algorithm that keeps the particle system alive, at the workshop on «Statistique des Modèles à Données Manquantes», held at université de Marne–la–Vallée in January 2005, at the «Probabilités et
Statistiques» seminar of université de Nice–Sophia Antipolis in April 2005, and at the Control seminar of the Department of Engineering of the University of Cambridge in October 2005. He has also given a talk on filtering a diffusion process observed in singular noise, at the joint
seminar on Stochastic Analysis, Random Fields and Applications and minisymposium on Stochastic Methods in Financial Models, organized in Ascona in May 2005.
V. Rossi has given a talk on nonlinear filtering using convolution kernels at the «Premières Rencontres des Jeunes Statisticiens» in Aussois in September 2005. He has also given a talk on applications of particle filtering in biological field at the «Journées de Statistique et
Applications en Biologie» organized at université de Rennes 2 in September 2005. He has also given a talk on the introduction of a selection step to avoid the degeneracy of particle filter algorithms at the colloquium «Statistique des Processus. Applications au Traitement du Signal et de
l'Image» held at Institut de Mathématiques Appliquées in Angers in September 2005.
Visits and invitations
F. Le Gland has been invited in October 2005 by Jan Maciejowski and Andréa Lecchini Visentini in the Department of Engineering of the University of Cambridge, and has given there a talk in the Control seminar on a sequential particle algorithm that keeps the particle system
alive.
Antoine Lejay, from the OMEGA project at INRIA Lorraine, has visited our group for three days in February 2005, and has given a talk on Monte Carlo methods for discountinuous and fractured media.
Agnès Lagnoux, a PhD student at the Laboratoire de Statistique et Probabilités of université Paul Sabatier, and Pascal Lezaud, from the joint CENA / ENAC department of applied mathematics have visited our group for two days in June 2005, and have given a talk each, on the
estimation of a rare event probability, and on an introduction to the theory of extreme values, respectively.
Mathias Rousset, a PhD student at the Laboratoire Jean–Alexandre Dieudonné of université de Nice–Sophia Antipolis, under the supervision of Pierre Del Moral, has visited our group in November 2005, and has given a talk about particle systems and out–of–equilibrium molecular
dynamics.
Rivo Rakotozafy, assistant professor at the University of Fianaranstoa, has been awarded by the French embassy in Antananarivo, Madagascar a grant to support three visits (one per year, each stay of three months duration) to prepare a Madagascar habilitation thesis (HDR) under the
supervision of Fabien Campillo. A related objective is to set up a collaboration between the University of Fianaranstoa and INRIA.
![]() and the asymptotic variance can be estimated using an appropriate central limit theorem. To reduce the asymptotic variance of the estimator, many variance reduction techniques have been proposed. However, running independent Monte Carlo simulations can lead to very poor results,
because trajectories are generated
blindly, and only afterwards are the corresponding weights evaluated, which can happen to be negligible in which case the corresponding trajectory is not going to contribute to the estimator, i.e. computing power has been wasted.
and the asymptotic variance can be estimated using an appropriate central limit theorem. To reduce the asymptotic variance of the estimator, many variance reduction techniques have been proposed. However, running independent Monte Carlo simulations can lead to very poor results,
because trajectories are generated
blindly, and only afterwards are the corresponding weights evaluated, which can happen to be negligible in which case the corresponding trajectory is not going to contribute to the estimator, i.e. computing power has been wasted.![]()
![]()
![]() , and the associated normalized nonlinear flow of probability distributions satisfies the dynamical system
, and the associated normalized nonlinear flow of probability distributions satisfies the dynamical system![]()
![]()
![]() , hence the unnormalized (linear) flow as well, can be expressed in terms of the normalized (nonlinear) flow : indeed
, hence the unnormalized (linear) flow as well, can be expressed in terms of the normalized (nonlinear) flow : indeed
![]() . To solve these equations
numerically, and in view of the basic assumption that it is easy to
simulater.v.'s according to the probability distributions
. To solve these equations
numerically, and in view of the basic assumption that it is easy to
simulater.v.'s according to the probability distributions
![]() , i.e. to mimic the evolution of the Markov chain, the original idea behind particle methods consists of looking for an approximation of the probability distribution
, i.e. to mimic the evolution of the Markov chain, the original idea behind particle methods consists of looking for an approximation of the probability distribution
![]()
![]()
![]() of particle positions and weights, and the algorithm is completely described by the mechanism which builds
of particle positions and weights, and the algorithm is completely described by the mechanism which builds
![]()
![]()
![]()
![]()
![]() , convergence as empirical processes indexed by classes of functions, uniform convergence in time (see also
,
), central limit theorem (see also
), propagation of chaos, large deviations principle, moderate deviations principle (see
), etc. Beyond the simplest
bootstrapversion of the algorithm, many algorithmic variations have been proposed
, and are commonly used in practice :
, convergence as empirical processes indexed by classes of functions, uniform convergence in time (see also
,
), central limit theorem (see also
), propagation of chaos, large deviations principle, moderate deviations principle (see
), etc. Beyond the simplest
bootstrapversion of the algorithm, many algorithmic variations have been proposed
, and are commonly used in practice :![]() are too much uneven.
are too much uneven.![]()
![]()
![]() , then computer power has been wasted, and it has been suggested to use importance sampling again in the mutation step, i.e. to let particles explore the state space under the action of an alternate wrong mutation kernel, and to weight the particles according to their likelihood for
the true model, so as to compensate for the wrong modeling. More specifically, using an arbitrary importance decomposition
, then computer power has been wasted, and it has been suggested to use importance sampling again in the mutation step, i.e. to let particles explore the state space under the action of an alternate wrong mutation kernel, and to weight the particles according to their likelihood for
the true model, so as to compensate for the wrong modeling. More specifically, using an arbitrary importance decomposition![]()
![]() is constant in a neighborhood of the set
is constant in a neighborhood of the set
![]() , in terms of the Kalman filter associated with the linear tangent linear Gaussian model, and (ii) the score function (i.e. the derivative of the log–likelihood function w.r.t. the parameter), evaluated at the true value of the parameter and suitably normalized, converges to a
Gaussian r.v. with zero mean and covariance matrix
, in terms of the Kalman filter associated with the linear tangent linear Gaussian model, and (ii) the score function (i.e. the derivative of the log–likelihood function w.r.t. the parameter), evaluated at the true value of the parameter and suitably normalized, converges to a
Gaussian r.v. with zero mean and covariance matrix
![]() .
.