Scientific Foundations
Concurrent constraint programming
The class of Concurrent Constraint programming languages (CC) was introduced a decade ago by Vijay Saraswat as a unifying framework for constraint logic programming and concurrent logic programming. The CC paradigm constitutes a representative abstraction of constraint programming
languages, and thus allows a fine grained study of their fundamental properties.
CC generalizes the Constraint Logic Programming framework (CLP) by introducing a synchronization primitive, based on constraint entailment. It is a model of concurrent computation, where agents communicate through a shared store, represented by a constraint, which expresses some
partial informationon the values of the variables involved in the computation. The variables play the role of transmissible dynamically created communication channels.
One of the big successes of CC has been the simple and elegant reconstruction of finite domain constraint solvers, and the cooperation of several models to solve a single combinatorial problem. On the other hand, to use CC for programming reactive applications forces one to abandon the
hypothesis of monotonic evolution of the constraint store; this is a strong motivation for new extensions of CC languages.
There are strong completeness theorems relating the execution of a CLP program and its translation in classical logic, which provide smooth reasoning techniques for such programs. However these theorems are broken by the synchronization operation of CC. Looking for a logical semantics of
CC programs in the general paradigm of logic programming,
program = logical formula,
execution = proof search,
leads to a translation in Jean-Yves Girard's linear logic. This allows the recovery of some completeness results about successes and stores; even suspensions may be characterized with the non-commutative logic of Ruet and Abrusci.
It is thus possible to address important issues for Constraint Programming:
verifying CC programs;
combining CLP and state-based programming;
dealing with local search inside a global constraint solving procedure.
The last two cases rely on a natural extension of CC languages, called Linear Concurrent Constraint languages (LCC), which simply replaces constraint systems built onto classical logic by constraint systems built onto linear logic. This allows us to represent state changes thanks to the
consumption of resources during the synchronization action, modeled by the linear implication.
Constraint solvers
Our domains of application use quite different constraint systems:
finite domains (bounded natural numbers): primitive constraint of some finite domain membership, numerical, symbolic, higher order and global constraints;
reals: Simplex algorithm for linear constraints and interval methods otherwise;
terms: subtyping constraints and ontologies;
temporal constraints: CTL and LTL formulae, either propositional or with numerical constraints.
The project works on constraint resolution methods and their cooperation. The main focus is the efficiency of constraint propagation methods, the design of global constraints and the combination of constraint propagation with local search methods.
Constraint programming environments
Handling hundreds of thousands of heterogeneous constraints on as many variables is impossible without tools specially designed to show the different views of the execution. We study the use of several software analysis tools to help to follow and understand what is going on during
constraint resolution. Our approach is based on two elements: a generic XML based trace format for constraints (Gentra4CP) to keep and store execution traces, and the use of different and original kinds of man-machine-interface analysis techniques, mainly based on the visualization of large
graphs and trees.
Semantics based debugging, static and dynamic typing, and more generally validation of CC programs are also studied in the project. Concerning typing issues in constraint programming, the usual coercions between constraint domains (e.g. between booleans and integers, lists and terms) offer
a particularly challenging task to type systems design.
Systems biology
Systems biology is a cross-disciplinary domain involving biology, computer science, logics, mathematics, and physics to elucidate the high-level functions of the cell from their biochemical bases at the molecular level.
At the end of the Nineties, research in Bioinformatics evolved, passing from the analysis of the genomic sequence to the analysis of post-genomic interaction networks (expression of RNA and proteins, protein-protein interactions, etc). The complexity of these networks requires a large
research effort to develop symbolic notation and analysis tools for biological processes and data. In order to scale-up, and get over the complexity walls to reason about biological systems, there is a general feeling that beyond providing tools to biologists, computer science has much to
offer in terms of concepts and methods.
We are interested in the modeling and analysis of complex molecular processes in the cell, at different levels of abstraction, qualitative and quantitative. The most original aspect of our research can be summarized by the following identifications:
biological property = temporal logic formula,
biological validation = model-checking.
Our main research axis is thus to apply logic programming concepts and circuit design technologies to cell molecular biology.
Application Domains
Combinatorial optimization problems
The number and economic impact of combinatorial optimization problems found in the industrial world are constantly increasing. They cover:
resource allocation;
placement;
scheduling;
planing;
transport;
etc.
The last forty years have brought many improvements in Operations Research resolution techniques. In this context, Constraint Programming can be seen as providing, on the one hand, local consistency techniques that can be applied to various numerical or symbolic constraints, and on the
other hand, declarative languages. This last point is crucial for quickly developing complex combinations of algorithms, which is not possible without a language with a high level of abstraction. It allowed for better results, for instance in scheduling problems, than traditional methods, and
is promised to an even better future when thinking about the cooperation of global resolution, local consistency techniques and search methods.
The project builds upon its knowledge of CC languages, constraint solvers and their implementation to work in these directions. The LCC paradigm offers at the same time a theoretical framework for analysis, and a valuable guide for practical language design and implementation. The work on
programming environments helps to integrate the Constraint Programming tools into this application domain.
In-silico cell
In 2002 , we started a Collaborative Research Initiative ARC CPBIO on ``Process Calculi and Biology of Molecular Networks''. By working on well understood biological models, we sought:
to identify in the family of competitive models coming from the Theory of Concurrency
 -calculus, Join-calculus and their derivativesand from Logic Programming
Constraint Logic Programming, Concurrent Constraint languages and their extensions to discrete and continuous time, TCC, HCC, the ingredients of a language for the modular and multi-scale representation of biological
processes;
-calculus, Join-calculus and their derivativesand from Logic Programming
Constraint Logic Programming, Concurrent Constraint languages and their extensions to discrete and continuous time, TCC, HCC, the ingredients of a language for the modular and multi-scale representation of biological
processes;
to provide a series of examples of biomolecular processes transcribed in formal languages, and a set of biological questions of interest about these models;
to design and apply to these examples formal computational reasoning tools for the simulation, the analysis and the querying of the models.
This work lead us to the design and implementation of the Biochemical Abstract Machine BIOCHAM that has the unique feature of providing formal languages corresponding to different qualitative and quantitative levels of abstraction, for, on the one hand, modeling biomolecular interaction
diagrams with reaction rules, and on the other hand, modeling the biological properties of the system in temporal logic. This double formalization of both the model and the biological properties of the system at hand opens several new research avenues on the design and systematic validation
of biological models.
We participate in two European Projects of the 6th PCRD. First the STREP
[APrIL II]where the main objective is to apply probabilistic inductive logic programming techniques
to bioinformatics applications. Our main focus is on the regulatory and metabolic networks in the cell, and the semi-automatic completion or revision of models from observed temporal properties of the system
[REWERSE], in which we focus, among other themes, on bioinformatics as a field of application of
the new Semantic Web technologies based on rules and constraints
[GO]in order to improve the re-use and composition of models, as well as the semi-automatic
correction/completion of models.
Software
BIOCHAM
Nathalie
Chabrier-Rivier
François
Fages
Sylvain
Soliman
The Biochemical Abstract Machine
[BIOCHAM]is a modeling and validation environment for molecular systems biology.
BIOCHAM provides precise semantics to biomolecular interaction maps at three abstraction levels:
the boolean semantics of molecules presence and absence,
the continuous semantics of molecular concentrations,
the stochastic semantics of molecule populations.
Based on this formal framework, BIOCHAM offers:
a compositional rule-based language for modeling biochemical systems, allowing patterns and kinetic expressions when numerical data are available;
numerical and boolean simulators;
a temporal logic language (CTL for qualitative models and LTL with numerical constraints for quantitative models) for formalizing biological properties such as reachability, checkpoints, oscillations or stability, and checking them automatically with model-checking techniques;
automatic search procedures to infer interaction rules and parameter values from known temporal properties of the system.
BIOCHAM is fully implemented in GNU-Prolog and interfaced to the state-of-the-art symbolic model checker
[NuSMV]for evaluating boolean CTL queries in large models over several hundreds of variables.
BIOCHAM models can be imported from, and exported to, the standard Systems Biology Markup Language
[SBML].
TCLP
Emmanuel
Coquery
[TCLP]is a prescriptive type system for Constraint Logic
Programming, currently: ISO-Prolog, GNU-Prolog, SICStus Prolog and the constraint programming libraries of SICStus Prolog. TCLP can also type check constraint solvers written in the
Constraint Handling Rules(CHR) language.
The flexibility of the TCLP type system is obtained by the combination of three kinds of polymorphism: parametric polymorphism (e.g.
list(A)), subtyping (e.g.
list(A)
<term) and overloading (e.g.
-:num
*num
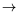 numand
-:A
*B
numand
-:A
*B
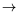 pair(A,B)). No type declaration are required, thanks to a type inference algorithm for predicates and to a default
termtype for function symbols.
pair(A,B)). No type declaration are required, thanks to a type inference algorithm for predicates and to a default
termtype for function symbols.
GNU-Prolog
Daniel
Diaz
Rémy
Haemmerlé
[GNU Prolog]is a free Prolog compiler with constraint solving over finite domains developed by
Daniel Diaz. GNU Prolog accepts Prolog extended with primitives for constraint programming and produces native binaries (like gcc does from a C source). The Prolog part conforms to the ISO standard for Prolog with many practical extensions (global variables, OS interface, sockets,...). GNU
Prolog also includes an efficient constraint solver over Finite Domains (FD), giving the user the combined power of constraint programming and the declarativity of logic programming.
An experimental version, called GNU-Prolog-RH, is developed as an extension introducing concurrency, attributed variables, and constraint solving over the reals. This version greatly extends the expressive and modeling power of GNU-Prolog. It is also used to prototype the design and
implementation of our new SiLCC language.
CLPGUI
François
Fages
[CLPGUI]is a generic graphical user interface written in Java for constraint
logic programming. It is available for GNU-Prolog and SICStus Prolog. CLPGUI has been developed both for teaching purposes and for debugging complex programs. The graphical user interface is composed of several windows: one main console and several dynamic 2D and 3D viewers of the search tree
and of finite domain variables. With CLPGUI it is possible to execute incrementally any goal, backtrack or recompute any state represented as a node in the search tree. The level of granularity of the search tree is defined by annotations in the CLP program.
Tra4CP
Pierre
Deransart
Following the former OADymPPaC project
[Tra4CP](Traces for Constraint Programming). The objective of this
sourceforge projectproject is to build a repository of constraint resolution traces and visualization tools. The purpose is to disseminate the results of the former
[OADymPPaC]project and to facilitate contacts and working exchanges between
researchers in the field of complex problem solving using constraint programming.
Adaptive search library
Daniel
Diaz
This is a C
[library]to solve constraint satisfaction problems by an adaptive local search
method. The current release is limited to permutation problems. More precisely, all
nvariables have the same domain
x1..
xnand are subject to an implicit all-different constraint. Several problems fall into this category and some examples are provided with the library.
New Results
Implementation of SiLCC
François
Fages
Rémy
Haemmerlé
Daniel
de Rauglaudre
Sylvain
Soliman
We are developing SiLCC an imperative and concurrent constraint programming language based on a single paradigm: the one of Vijay Saraswat's concurrent constraint programming extended with constraint systems based on Jean-Yves Girard's Linear Logic. In the late 90's we developed the theory
of this extension and we have now begun its implementation.
From a constraint programming point of view, the unique combination of constraint programming with imperative features opens many new possibilities, among which:
the capability of programming constraint solvers in the language, making them extensible by the user,
making a fully bootstrapped implementation of a constraint programming language (for the first time since Prolog)
combining constraint reasoning with state change;
proving program correctness using Linear Logic.
Our current implementation of SiLCC
Module System for SiLCC
François
Fages
Rémy
Haemmerlé
Sylvain
Soliman
In the context of the implementation of SiLCC, we are working on a module system for concurrent constraint logic programming languages. Our first contribution has been the design of a secure module system for constraint logic programs
We are currently developing an extension of this preliminary module system in which modules are first class objects. In this system, primitive operators of LCC allow us to natively express notions of environment and hiding, and to unify modules, functors and closures as a particular case
of LCC agents.
Type systems for constraint logic languages
Emmanuel
Coquery
François
Fages
Rahul
Narain
The
Constraint Handling Rules(CHR) are an untyped rewrite rule language, initially designed for implementing constraint solvers. In order to benefit from type programming for the development of larger programs, we have designed a generic type system for CHR
This work addresses also some typing issues concerning the semantic web languages investigated in the Rewerse network of excellence. Xcerpt is a Web query language based on rules and non-deterministic pattern matching for semi-structured XML data. In collaboration with Sacha Berger from
the University of Munich, Włodzimierz Drabent from the Polish Academy of Sciences and Artur Wilk from Linköping University, we propose a set of typing rules for Xcerpt
Global constraint of scheduling with concentration constraints
François
Fages
Sadhika
Sharma
Aurélie
Strobbe
In collaboration with TOTAL, we study an optimization problem of crude oil blending in refineries. The problem is to find a plan of transfer and mixing of crude oil, from the boats to the distillation units through storage and mixing tanks, under various constraints of product
concentrations, continuous distillation, schedule, and optimization criteria. This NP-hard problem is the combination of a planning problem (for choosing the transfer tasks and quantities) with a scheduling problem.
Previous approaches based on Mixed-Integer Linear Programming (MILP) rely on a discretization of time that may give infeasible or suboptimal solutions. On the other hand, a constraint programming approach is appealing for its capability to treat efficiently the scheduling part of the
problem without time discretization, We have developed such a solution with ILOG tools, by introducing a global constraint of scheduling with concentration constraints, and using heuristics for the planning part of the problem.
Because of the importance of the heuristics part on real-size data, we are also considering a constraint-based local search method for this problem.
Multi-user distributed resource allocation problems
François
Fages
Loïc
Fosse
Sylvain
Sécherre
In collaboration with Evelyne Lutton (COMPLEX Team).
The problem of office assignment on the INRIA Rocquencourt campus can be considered as a difficult constraint satisfaction problem: the demand of research teams exceeds the actual resource, and in the same time the constraints and preferences of each team are difficult to define and deal
with. Since 2003, in collaboration with COMPLEX team, we have developed a multi-user interactive optimization approach to this problem, based on constraint-based local search for computing solutions, and on genetic algorithms for learning the user preferences from their notations of the
proposed solutions.
This year, we have shown that the user preference learning problem could be solved exactly with a linear program, under the assumption that the scores given by the user are a linear combination of criteria. The constraint error functions used in the adaptive search procedure have also been
rewritten and a new prototype has been completely re-implemented in SCILAB, showing the capability of the system to propose interesting solutions
Continuous dynamics in BIOCHAM
Laurence
Calzone
François
Fages
Neha
Mittal
Sylvain
Soliman
The Biochemical Abstract Machine
[BIOCHAM]
Classical numerical integration methods (Runge-Kutta and Rosenbrock's implicit method for stiff systems) were implemented in GNU-Prolog to deal with the ordinary differential equations (ODEs) derived from the kinetics of the reactions. With values for the initial concentrations BIOCHAM
thus proposes a deterministic time series (with fixed or variable step size) describing the evolution of the system. Taking this time series as a linear Kripke structure allows us to use model-checking techniques for LTL queries
Current work involves:
using this model-checking features for learning parameter values, as explained in section
identifying precisely which fragment of first-order LTL is wanted;
formalizing, as an abstraction, the relationship between the continuous and boolean semantics;
defining more precisely the relationship with the stochastic level of section
using bifurcation theory to gain information about possible parameter values for certain behaviors of the system, and elucidating how to connect LTL with ``types of bifurcations''.
Stochastic dynamics in BIOCHAM
François
Fages
Loïc
Fosse
Sylvain
Soliman
Following the same ideas as above, a third abstraction level has been added to BIOCHAM for specifically with low numbers of molecules. The population semantics associates to each compound its
number of moleculesin the system, and to rules a continuous time Markov chain
Probabilistic model-checking was considered to query the properties of such a system, but even state-of-the-art PCTL model-checkers like PRISM did not scale up to treat simple BIOCHAM models. Stochastic simulation techniques,
a laGillespie, were then used to provide, once again, linear Kripke structures on which LTL model-checking can be handled as in section
Learning reaction rules in BIOCHAM
Laurence
Calzone
Nathalie
Chabrier-Rivier
François
Fages
Sylvain
Soliman
The formalization of biomolecular interactions in BIOCHAM syntax, and the specification of the observed behavior of the system in temporal logic (CTL or LTL) make it possible to develop machine learning algorithms to automatically correct or complete existing models. It is worth noting
that structural learning of reaction rules from temporal logic properties is quite new, both from the machine learning perspective and from the systems biology perspective.
In the framework of the APrIL II STREP, we first applied state-of-the-art inductive logic programming tools to simple reachability properties. The objective was to complete a boolean BIOCHAM model to satisfy a CTL specification. We developed a more powerful search algorithm for learning
new reaction rules from general temporal logic properties. This algorithm evolved into a theory revision algorithm, taking into account that ACTL and ECTL formulae (i.e. those where the only path operator is respectively
Aand
E) can guide the search for the addition or deletion of rules
In the quantitative case, the same strategy can be applied to learn kinetic parameter values. Once the biological properties of a system under various initial conditions, are described both qualitatively and quantitatively with LTL formulae and constraints, an enumerative algorithm can be
applied to estimate parameter values by model-checking
Current work concerns:
inferring the types of molecules (kinases, phosphatases,...) involved in a model, and guiding the search of rules additions and deletions using this information;
using information obtained from a bifurcation diagram (see section
defining a measure of how well an LTL specification is satisfied, in order to be able to use gradient methods to speed up the search.
Coupled model of the cell cycle and the circadian cycle in mammalian cells
Laurence
Calzone
Sylvain
Soliman
Recent advances in cancer chronotherapy techniques support the evidence that there exist some links between the cell and the circadian cycles. Both cycles have been successfully modeled, however, as of today, there are no precise models describing the coupling of the two cycles. One
purpose of a coupled model is to better understand how to efficiently target malignant cells depending on the phase of the day.
For this study, we interact with the group of A. Goldbeter from ULB and with J. Clairambault of the BANG team. Our model is built from two models, a model of the circadian cycle from Leloup and Goldbeter and a generic model of the cell cycle model focusing on a crucial event, the
entry into mitosis. Currently, the model is focused on the coupling through the WEE1 kinase. This protein plays an important role in the regulation of the activity of MPF, a complex crucial in cell division. The WEE1 kinase seems to be regulated positively by CLOCK/BMAL1 and negatively by
CRY, these three genes being well-known circadian core genes.
The BIOCHAM feature for learning parameter values under period constraints was introduced for this study. This allowed us to compute the domain of entrainment of the cell cycle by the circadian cycle. This domain mainly depends on the strength of the WEE1 kinase, regulated by circadian
genes, on the activity of MPF. We now intend to incorporate other links, based on evidence from the literature: through the protein c-MYC for instance; and to make the generic cell cycle model more complete in order to see the effect of these other links.
Space in BIOCHAM
Sakina
Ayata
Laurence
Calzone
François
Fages
Sylvain
Soliman
Until now, BIOCHAM did not consider the spatial distribution of the molecules. During simulations, all molecules were considered as being either homogeneously mixed together or implicitly localized so that reactions occur like in a molecular soup. But in the cells, molecules are localized
and do not necessarily have the same activity in different locations. Moreover transport phenomena induce reaction delays and concentration changes, which may impact the behavior of the system.
A purely symbolic notion of locations has been introduced in BIOCHAM in order to model spatial phenomena
An example of transport rules in the p53/mdm2 model and an example of cell to cell signalling have been developed with this version of BIOCHAM. More efficient techniques are under investigation to deal efficiently with large number of locations.
Protein dynamics in growth of fission yeast cells
Laurence
Calzone
In collaboration with Michel Kerszberg, from Paris VI University (UMR CNRS 7138), we are currently developing a model of the dynamics of proteins responsible for the polarity in fission yeast cells (
schizosaccharomyces pombe). The model is both spatial (2D) and stochastic, and thus complements nicely the other type of modeling described in the previous section. Using the
ctrl-devsoftware tool of M. Kerszberg, we try to understand the mechanics of growth, polarity and septation (division) of fission yeast cells.
Building on results coming mainly from mutations, we concentrate on two proteins that seem to play a major role in the process. The first one,
tea1p, present in the cytoplasm binds to and moves along microtubules until it is deposited to the cell cortex by binding to a membrane protein,
mod5p. Once in complex, tea1p is able to recruit polarity factors orienting the direction of growth in the cell.
We hope to explain, thanks to this model, some of the principles of growth in yeast cells. Another interesting aspect of this analysis is to measure the importance and differences of stochastic modeling as opposed to continuous modeling. We also hope to gain from such a spatial model a
better insight into the needed features for a richer notion of locations in BIOCHAM.
![]() -calculus, Join-calculus and their derivatives
-calculus, Join-calculus and their derivatives