Scientific Foundations
Scientific Foundations
The scientific objective of the COPRIN project is to develop and implement systems solving and optimization algorithms based on constraints propagation methods, interval analysis and symbolic computation, using interval arithmetics as the primary tool.
The results obtained with these algorithms are certified in the sense that no solution can be missed and that, for 0-dimensional system solving, solutions can be calculated with an arbitrary accuracy. Furthermore, some of our algorithms allow us to deal with systems involving uncertain
coefficients.
A system is constituted by a set of relations that may use all the usual mathematical operators and functions (hence we may deal, for example, with the relation
sin(
x+
y) + log(cos(
e
x) +
y2)
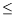 0).
0).
We are interested in real-value constraint satisfaction problems ((
f(
X) = 0,
f(
X)
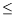 0)), in optimization problems and in proving the existence of properties (for example,
0)), in optimization problems and in proving the existence of properties (for example,
Xsuch as
f(
X) = 0or two values
X1,
X2such as
f(
X1)>0and
f(
X2)<0).
Solutions are searched within a finite domain (called a
box) which may be either continuous or mixed (i.e. for which some variables must belong to a continuous range while other variables may only have value within a discrete set). Importantly, we are trying to find all the solutions within the domain as soon as the computer arithmetics
allow it: in other words we are looking for
certifiedsolutions. For example, for 0-dimensional system solving, we provide a domain that includes one, and only one, solution, together with a numerical approximation of this solution, which may be refined at will, using multi-precision.
Our approach aims at developing various operators that will be applied in sequence on a box:
exclusion operators: these operators determine that there is no solution to the problem within a given box
contractors: these operators may reduce the size of the box, i.e. decrease the width of the variables' allowed ranges
existence operators: these operators allow to determine that there is a unique solution within a given box and are usually associated with a numerical scheme that enables to compute this solution safely
If a given box is not rejected by the exclusion operators and is not modified by the other operators, then we will bisect one of the variables in order to create two new boxes that will be processed later on. Methods for choosing the bisected variable also clearly fall within the scope of
the project.
Our research aims at developing operators that can be used for any problem or are specific to a given class of problem, especially problems that are issued from application domains for which we have an internal expertise (such as mechanism theory and software engineering).
We are also studying symbolic computation based methods in order to:
develop a user-friendly interface that will automatically generate and run an executable program, and return the result to the interface;
analyze the semantic and syntax of the relations involved in a problem, so as to automatically generate specific operators, or to obtain a better interval evaluation of the expressions (as the evaluation of an expression using interval arithmetics is very sensitive to the expression
syntax)
in order to allow for the calculation of the solutions with an arbitrary accuracy. For this purpose two approaches are currently being used:
certified interval solutions are obtained through a compiled solving program, and then a symbolic computation procedure is used to calculate the solutions up to the desired accuracy
a multi-precision interval arithmetics package is used within a symbolic-numeric solving program and allows to obtain the solutions with an arbitrary accuracy
The first approach is usually much faster than the second one (by a factor of approximately 1,000 to 10,000) but may fail to determine solutions if the system is numerically badly conditioned, while the second approach will always find the solutions, although the computation time may
be problematic.
New Results
Robotics and mechanism theory
robotics
calibration
robot accuracy
mechanism theory
parallel robots
The core of our activities in robotics and mechanism theory is the optimal design of mechanisms and the analysis of parallel robots
the long-term work on parallel robot's optimal design
kinematics analysis and design of parallel robots using cams as passive constraints for the legs
a theoretical analysis of the use of classical accuracy indexes for parallel robots
Meanwhile, a long term research effort continues on finding a solving method for distance equations, and on wire robots (i.e. robots whose actuators are constituted of wires whose lengths may change).
Optimal design of parallel robots with respect to workspace and accuracy requirements
Jean-Pierre
Merlet
Fang
Hao
David
Daney
Our methodology for optimal design is to determine an approximation of the domain including all the possible values of the
ndesign parameters, so that any design requirement (or a set of them) may be satisfied. Such approximation is obtained as a set of boxes in the parameter space, an
ndimensional space in which each axis represents the value of one design parameter. If a domain approximation
Aiis obtained for any design requirement
Riin the set of requirements, then the possible design parameter values will be obtained as the intersection of all the
Ai
it allows to deal with
imperativerequirements, i.e. requirements that necessarily need to be satisfied by a design solution
it allows to present various possible compromises between requirements that are antagonistic
it allows to deal with uncertainties: for example, the physical instance of a theoretical solution may differ because there are manufacturing tolerances. In our approach, the approximation only includes boxes which width is at least twice the manufacturing tolerances
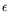
i. This allows to choose nominal values for the design parameters, so that the point representing their real values is still guaranteed to lie in a box.
However, this approach may somehow be difficult because we must calculate the approximation
Ai: and interval analysis would be a tool of choice. We have shown that it was possible to compute the
Aiin a 26-dimensional parameter space, so that the robot workspace will include a large, arbitrary set of pre-defined poses, while the robot's positioning errors at these poses will not be larger than a pre-defined threshold
Cams coupled parallel robots
Jean-Pierre
Merlet
Classically, parallel robot legs are submitted to passive constraint generated by higher kinematic pairs such as universal and spherical joints. But other passive constraints may be considered as well, and we have investigated the use of cams to impose passive constraints. The robot's
base and platform include pairs of arbitrary surfaces, that are constrained to lie in contact during the robot's motion. This type of robot may be used, for example, to model complex human joints, such as the knee. With such surface constraints, the robot's kinematics (i.e. the relations
between the actuated joint variables and the end-effector's pose) may become quite complex. An interval-based kinematic solver, which allows for the use of arbitrary constraint surfaces, has been developed and successfully tested.
The synthesis problem of such a robot was also addressed, with 1 d.o.f.: the problem is to determine the parametric constraint surfaces' parameters, so that the robot goes through specified way points
Accuracy indices
Jean-Pierre
Merlet
The analysis of accuracy for serial robots is a well established research domain. First the robot's Jacobian matrix, which relates sensor measurement errors to the end-effector's positioning errors, is established. Then, various accuracy indexes based on this matrix are calculated (such
as the manipulability index or the condition number). These indexes may be local (i.e. valid for one given pose) or global (i.e. valid over a given workspace). Until now these indexes have been used for parallel robots as well, the duality between serial and parallel robots only imposing
the use of the robot's inverse jacobian matrix instead of the jacobian matrix.
In theory, we have shown that this approach may not be valid. First, multiple inverse jacobian matrices may be defined, and not all of them include the same amount of information. For example, for robots with
n<6d.o.f, singularities may not all be described by the
n×
nmatrix relating the actuated joint velocities with the end-effector velocities. We also considered the classical accuracy indexes and showed that they did not always give consistent accuracy ranking when they are calculated for a given set of poses. Indeed we are
able to calculate the maximal positioning errors of the end-effector at a given pose and hence to order the poses according to their accuracy: we then expect the accuracy indexes to reflect this ranking and this is not what has been observed. Consequently, we proposed new, global,
consistent accuracy indexes, but we showed that their calculation is a challenging task
Wire robot
Jean-Pierre
Merlet
David
Daney
Marc
Gouttefarde
Viorel
Ciauscu
We intend to build a wire robot that will be used as a force-feedback haptic device for the workbench of the research unit. Although several wire robots have been developed in many laboratories, most suffer from a lack of precision and flexibility. Indeed, performance requirements may
slightly change between two virtual reality tasks, and it is not realistic to assume that a system with a fixed geometry may be able to deal with all of them. To solve these problems, we focused on the following objectives:
mechanical design: the wire actuation system should be designed to allow fast changes in the robot's geometry, a precise evaluation of wire lengths (for optimal measurement of the platform location) and of the force applied at the end-effector level, together with the possibility
of quickly modifying the maximal change in the wire lengths
modularity: the performances of a parallel robot are very sensitive to the robot's geometry. We intend to develop algorithms allowing to determine the robot's optimal geometry, given the task requirements. The relations between the force limitations (the wire can only pull and
its tensions are limited) and the workspace are currently being investigated by M. Gouttefarde.
The necessary hardware has been studied and the robot's mechanical construction will start early in 2006.
Calibration of a 4-RPR planar robot
David
Daney
correspondant
Yves
Papegay
Jean Pierre
Merlet
calibration
numeric-symbolic tools
Identification of a 4-RPR planar robot's kinematic parameters is a basic problem, which in turn illustrates a core issue of parallel robot calibration: the calibration equations involve both kinematic parameters that have to be identified and variables that are specific for each
calibration configuration. To reduce the size of the system and the number of unknown variables the classic approach is to manipulate the calibration equations in order to get a smaller set of equations that involves a reduced number of pose-dependent variables. However, this approach has
drawbacks: the elimination is not simple to perform (the equations are highly non linear) and the resulting equations, that are largely more complex than the initial set, may be badly numerically conditioned. We have compared classic elimination strategies (1), elimination based on an
algebraic formulation for the calibration equations (2) and a calibration algorithm based on the initial set of calibration equations (3). Method (3) applied to the 4-RPR planar robot leads to the best result. This research was performed in collaboration with I. Emiris of Athens University,
within the framework of a PAI Platon.
Another item of research addressed the problems of calibration strategies and of checking the validity of the robot's kinematic model, used to obtain the calibration equations. The calibration equations are obtained by setting the robot in various calibration configurations and partially
measuring the robot's state, using its proprioceptive sensors
 , where
, where
 are the kinematic parameters to be identified;
are the kinematic parameters to be identified;
 the unknown pose parameters;
the unknown pose parameters;
 the robot's unmeasured state parameters; and
the robot's unmeasured state parameters; and

mthe measured state parameters. A calibration equation is obtained for each of the
ncalibration configurations and as the measurements are uncertain, the kinematics parameters are obtained as the ones that minimize
 . Using experimental data, we have shown that this approach leads to a paradox: the calculated
. Using experimental data, we have shown that this approach leads to a paradox: the calculated
 may be such that some calibration equations will not be satisfied whatever the measurement values within their uncertainty ranges (which are known). We suggest, instead, an interval-based approach that allows to determine the set
may be such that some calibration equations will not be satisfied whatever the measurement values within their uncertainty ranges (which are known). We suggest, instead, an interval-based approach that allows to determine the set
 of all possible values of
of all possible values of
 so that all calibration equations may be satisfied
so that all calibration equations may be satisfied
A second problem is that simplifying assumptions are used to establish the robot's kinematic model (e.g. that joint axes are parallel or perpendicular), as otherwise, the model might become very complex. However, the validity of these assumptions has to be checked; for example if the set
 is empty, i.e. the kinematic model is not valid, the kinematic model's level of error must be ascertained. As a consequence, we suggested an index that measures how much the calibration equation has to be modified so that
is empty, i.e. the kinematic model is not valid, the kinematic model's level of error must be ascertained. As a consequence, we suggested an index that measures how much the calibration equation has to be modified so that
 is not empty anymore
is not empty anymore
Interval evaluation of kinematic equations
David
Daney
correspondant
Thomas
Adelmar
kinematics
interval analysis
A challenging problem in robotics is to certify manipulators' performances. These performances are dependent upon the robot's nominal geometry, but clearance and manufacturing tolerances also have a very negative influence and should be taken into account.
Statistical tools cannot be applied to performance evaluation as tolerances and clearance do not follow classic statistical distribution such as Gaussian distribution. However, it is usually possible to obtain uncertainty ranges. Then, interval analysis methods may be used to check a
given robot's kinematic performance.
Robot geometry is usually described with Denavit-Hartenberg parameterization. We have developed a dedicated kinematic equations' interval evaluation based on the Denavit-Hartenberg model. We are using this model's particular structure to provide a sharp evaluation of these equations.
Interval analysis for control theory
David
Daney
Odile
Pourtallier
correspondant
eigenvalue
polynomial
complex root
Gershgorin
exclusion method
A lot of research has been done in the field of system theory, specifically in order to analyze linear systems' stability,
i.ein order to study the state matrix's eigenvalues, or, equivalently, its polynomial transfer function's zeros. Nevertheless, we know that the stability or instability of a system is highly sensitive to data,
i.e.to the coefficients of the state matrix or the coefficients of the system's transfer function. One of the consequences is the fact that two types of problems arise when using numerical methods for dealing with the stability analysis of a system. The first problem is related to
numerical certification. In fact, the errors due to numerical rounding in a computer may have an impact on the final result of a system's stability. The second problem is related to modeling errors. Usually, the system (through its state matrix or its polynomial transfer function) is only
known with some errors (uncertainty). Hence the
realsystem is known to belong to a set of systems. More precisely, the state matrix is known to belong to some interval matrix, or the polynomial transfer function is known to belong to a set of polynomials with interval coefficients. An important point is to address the stability
problem of a whole set of systems and to be able to determine with certainty whether any matrix in a set described by an interval matrix is stable or unstable.
Interval analysis is a good tool to handle these kinds of problems since it considers not a single
object, but some
interval objects, here interval matrices or interval coefficient polynomials.
We selected some methods, within the large range of existing methods used for analyzing linear systems' stability, that could be extended to uncertain systems. We mainly worked with the extension and optimization of the Gershgorin circles method, and some exclusion methods (specifically
using Dedieu and Yakoubsohn exclusion functions). The first numerical tests are promising.
Meanwhile, we started programming the global optimization methods, using interval approach. This will be useful for the final implementation of the above-mentioned stability analysis method. This particular research is being performed in collaboration with S. Icart of the I3S
laboratory.
Interval analysis for optimization
An Efficient and Safe Framework for Solving Optimization Problems
Yahia
Lebbah
Claude
Michel
Michel
Rueher
optimization
interval analysis
numerical robustness
Interval methods have shown their ability to accurately locate and prove the existence of global optima safely and rigorously, but unfortunately, these methods are rather slow. Many efficient solvers for optimization problems are based on linear relaxations. However, these relaxations
are numerically ill-conditioned, and thus may overestimate, or worse, underestimate, global minima. We have developed
QuadOpt, an efficient and safe framework to rigorously bind the global optimum as well as the corresponding values for the parameters
Symbolic tools for modeling and simulation
Yves
Papegay
modeling
simulation
symbolic computation
code generation
accuracy
reliability
This research represents the main body of a long-term on-going collaboration with Airbus, whose objective is to directly translate the work of aeronautics engineers into digital simulators, in order to make aircraft design more efficient. This project already has applications in the
aircraft making development departments.
Modeling and simulation processes usually begin with using scientific theories for describing physical features with formula and computation algorithms. Using these models, numerical codes are implemented in order to simulate and visualize features. In an industrial context, the large
number of parameters and equations involved in models make the whole process very long, complex and expensive, especially as safe and reliable codes are required.
Previous research led to a model edition environment, based on symbolic computation tools, which makes it possible to enter models' formula and algorithms and validate them numerically on a reduced set of data. From then on, we tried to use these models to fully and automatically generate
a numerical real-time simulation engine to be plugged into flight simulators, while bringing out technical documentation associated with such simulations, which is a necessary tool for corporate memory.
A first prototype of C code generation for real-time simulation was designed last year. In 2005, we mainly worked on
scheduling of sub-model evaluation in large models,
instantiation of generic models,
optimization of the generated C code,
and we extended our prototype to a more robust and complete tool. Our long-term objectives are to use the computational model
to perform an automated sensitivity analysis (to find out which of the model's parameters have the largest influence on the output)
to determine the parameters' possible values, so that the model's output satisfies given constraints
Distance equations
distance equations
inner approximation
Solver for distance equations
Jean-Pierre
Merlet
A distance equation describes that the distance between two points in a
n-dimensional space is known, while the coordinates of at least one of these points are unknown. Systems of distance equations frequently occur in robotics, but also in other domains such as molecular biology.
Within the
ALIASlibrary, we have developed a distance equations solver that may be used for this problem. It features specific versions of most of the theorems that we are using within our general purpose solvers, and that have been revisited for distance equations, leading to stronger
versions of the theorems. For example, unicity regions (i.e. the regions in which there is a unique solution that may be safely computed using a given iterative scheme) obtained with the Kantorovitch theorem or Neumaier exclusion theorem are usually about 20 times larger than those obtained
with the general purpose version. This solver was used, for example, to efficiently solve the difficult problem of parallel robots' direct kinematics.
This solver was somewhat improved recently
Uncertainty management in distance equations
Carlos
Grandon
Bertrand
Neveu
The aim of our research is to propose and study new approaches for solving distance systems equations, with uncertainties on the parameters. In this case, the problem does not have isolated solutions but its solution sets consist of a hyper volume. Our objective is to approximate the
solution set as accurately as possible. A classical approach for solving systems with uncertainties combines a filtering phase with a bisection phase in order to compute the solution sets' outer approximation.
We proposed and studied two approaches aimed at improving the results of the classic algorithms applied to distance equations
The second approach relies on a method for detecting inner boxes (boxes that are included inside the solution space of uncertain distance equations). Different methods for detecting inner boxes based on classic interval analyses, quantified elimination and generalized interval
arithmetics were implemented and analyzed. Preliminary results show that generalized interval arithmetics seems to be the most promising, even in terms of computation time.
All methods studied up to now give sufficient but not necessary conditions for detecting inner boxes in a system of distance equations. We are currently studying a new test based on generalized interval arithmetics and geometric considerations, in order to obtain necessary and sufficient
conditions, and we are also studying its general extension.
Modal intervals
Alexandre
Goldsztejn
generalized intervals
quantified constraints
Classic interval theory allows to rigorously deal with uncertain quantities, like measurement errors. The modal intervals theory provides a richer interpretation, which allows to deal with different quantifiers for uncertainties. As a consequence, it is a promising framework for the
approximation of quantified constraints.
In spite of its promising applications, modal intervals theory is not widely used, due to its complicated construction. We proposed a new formulation of modal intervals theory
Local search library
Bertrand
Neveu
Gilles
Trombettoni
local search
meta-heuristics
We have continued developing the C++
INCOPlibrary, implementing incomplete methods for solving combinatorial optimization problems. This library offers classic local search methods such as simulated annealing, tabu search as well as a population based method, Go With the Winners. Several problems were encoded, including
Constraint Satisfaction Problems, graph coloring, and frequency assignment.
A new and simple local search meta-heuristics named
IDW(Intensification - Diversification - Walk) was developed last year. The next move is selected through the exploration of only one part of the neighborhood, and the first move leading to a better or equal configuration is chosen. When no such move is found in that part of the
neighborhood, the algorithm selects a worsening move. The new version of the algorithm developed this year has two parameters. The first parameter is the size of the part of the neighborhood that is examined at each move (intensification). The second parameter defines which worsening
neighbor, called spare neighbor, to chose for escaping local minima when no better or equal neighbor has been found. The value of this parameter indicates how among many visited bad neighbors one selects the less worsening one, and consequently how much one deteriorates the evaluation
function for escaping a local minimum (diversification).
An automatic parameter tuning tool automatically determines the parameter values. This meta-heuristics gave good results on different benchmarks (graph coloring, car sequencing, frequency assignment ...)
Local search methods for problems with continuous variables
Bertrand
Neveu
Rahim
Belkacem
optimization
local search
meta-heuristics
Meta-heuristics are considered as interesting methods for solving combinatorial optimization problems when complete methods are intractable. The aim of this study is to extend these methods to global optimization problems with continuous variables, when classic complete methods such as
branch & bound are not efficient enough. One key issue is to define a neighborhood. We implemented a first prototype in Java, with the main common meta-heuristics (simulated annealing, tabu search), and tested them on benchmarks
Decomposition and solving of geometric constraints
Bertrand
Neveu
Gilles
Trombettoni
geometric constraints
constraint system decomposition
``Geometric constraint solving'' is a challenging problem appearing in several fields such as industrial drawing and computer aided design (CAD). One version of this problem can be defined as follows: finding one or several solutions (i.e., position, orientation, dimension) to a system
constituted of geometric objects (e.g., points, lines, planes) that are subjected to geometric constraints (e.g., incidences, parallelism, distances, angles). The corresponding equation system is generally non linear and sometimes non generic (i.e., with singularities). Symbolic and numerical
methods (Newton-Raphson, continuation) may have difficulties solving large real-life geometric constraint systems.
The most common approach to solving this problem is to adopt a ``divide and rule'' method, and to solve the obtained equation subsystems by numerical methods or, preferably, by hard-coded procedures corresponding to geometric theorems. Our long-term effort in this domain has resulted in
the following original contributions:
we designed a graph-based decomposition algorithm, called
GPDOF, and applied it to large scale geometric constraint systems extracted from a specific scene modeling problem in computer vision (an article on
GPDOFhas been submitted).
an algorithm, called Inter-Block Backtracking (
IBB), can construct a total solution by mixing the partial solutions found in the subsystems by an interval-based solver, whatever the used decomposition of the systems
We enjoy well established working relations with the computer geometry and CAD national research community. Moreover, we are currently setting up a comprehensive survey about geometric constraint systems' decomposition techniques, in collaboration with D. Michelucci in Dijon; P. Schreck
and P. Mathis in Strasbourg and C. Jermann in Nantes.
Long-term research will now focus on gathering all the available algorithmic bricks (decomposition algorithms; interval-based computation techniques, etc) in order to develop a new geometric constraint solver. This work is led by the COPRIN project in collaboration with several French
researchers.
Filtering and bisection strategies
Arc-consistency over continuous domains
Gilles
Chabert
Gilles
Trombettoni
Bertrand
Neveu
Filtering variable domains usually means narrowing the bounds, but some basic operators (such as projections) may also reveal "gaps" within intervals (i.e. domain where there is no solution to the problem at hand). It is interesting to know whether the presence of these gaps can
influence propagation algorithms, in order to achieve arc-consistency.
As a consequence, we pursued and finalized our work on box-set consistency, a method that overcomes the problem by combining hull consistency and a gap-guided splitting strategy
We also investigated a very different approach that avoids the subdivision problem by representing domains with unions of intervals. We devised a new class of partial consistencies over continuous CSPs related to unions of intervals, and derived an algorithm called
interval global consistency (IGC)
Efficient pruning technique based on linear relaxations
Yahia
Lebbah
Claude
Michel
Michel
Rueher
interval analysis
numerical robustness
systems solving
We introduced a new filtering algorithm for handling systems of quadratic equations and inequalities. Such constraints are widely used to model distance relations in numerous application areas, ranging from robotics to chemistry. Classic filtering algorithms are based upon local
consistencies and are thus often unable to achieve a significant pruning of the variables domains occurring in quadratic constraint systems. However, these approaches have a drawback, which comes from the independent handling of the constraints. We thus introduced a global filtering
algorithm, which works on a tight linear relaxation of the quadratic constraints, the Simplex algorithm being then used to narrow the domains. Since most implementations of the Simplex use floating point numbers and thus are numerically unsafe, we provided a procedure to generate a safe
linearization, and we also used a procedure worked out by Neumaier and Shcherbina to get a safe objective value when calling the Simplex algorithm. Using these two procedures prevents the Simplex algorithm from removing any solution while filtering linear constraint systems. Experimental
results on classic benchmarks show that this new algorithm yields a much more effective pruning of the domains than local consistency filtering algorithms
Bisection strategies
Heikel
Batnini
Claude
Michel
Michel
Rueher
bisection
consistency
Classic methods for solving numerical Constraints Satisfaction Problems (CSP) are based on branch and prune algorithms, a dichotomous enumeration process interleaved with consistency filtering algorithms. In many interval solvers, the pruning step is based on local consistencies
(Hull-Consistency, Box-consistency) or partial consistencies (kB-consistencies, Bound-consistency). The associated pruning algorithms may identify gaps within some domains, i.e. inconsistent intervals that are strictly included in the domain. However, the identification of such gaps is not
generally used in bisection strategy, neither when choosing the bisected variable nor the the bisected range cutting point. We introduced a search strategy, named
MindTheGaps
![]() 0).
0).![]() 0)), in optimization problems and in proving the existence of properties (for example,
0)), in optimization problems and in proving the existence of properties (for example,