Overall Objectives
Overall Objectives
hidden Markov model (HMM)
particle filtering
risk evaluation
localisation
navigation and tracking
rare event simulation
The scientific objectives of ASPI are the design, analysis and implementation of interacting Monte Carlo methods, also known as particle methods, with focus on
statistical inference in hidden Markov models, e.g. state or parameter estimation, including particle filtering,
risk evaluation, including simulation of rare events.
The whole problematic is multidisciplinary, not only because of the many scientific and engineering areas in which particle methods are used, but also because of the diversity of the
scientific communities which have already contributed to establish the foundations of the field : target tracking, interacting particle systems, empirical processes, genetic algorithms
(GA), hidden Markov models and nonlinear filtering, Bayesian statistics, Markov chain Monte Carlo (MCMC) methods, etc. Intuitively speaking, interacting Monte Carlo methods are sequential
simulation methods, in which particles
explorethe state space by mimicking the evolution of an underlying random process,
learnthe environment by evaluating a fitness function,
and
interactso that only the most successful particles (in view of the value of the fitness function) are allowed to survive and to get offsprings at the next generation.
The effect of this mutation / selection mechanism is to automatically concentrate particles (i.e. the available computing power) in regions of interest of the state space. In the
special case of particle filtering, which has numerous applications under the generic heading of positioning, navigation and tracking, in target tracking, computer vision, mobile robotics,
ubiquitous computing and ambient intelligence, sensor networks, etc. each particle represents a possible hidden state, and is multiplied or terminated at the next generation on the basis of its
consistency with the current observation, as quantified by the likelihood function. These genetic–type algorithms are particularly adapted to situations which combine a prior model of the
mobile displacement, sensor-based measurements, and a base of reference measurements, for example in the form of a digital map (digital elevation map, attenuation map, etc.). In the most
general case, particle methods provide approximations of probability distributions associated with a Feynman–Kac flow, by means of the weighted empirical probability distribution associated
with an interacting particle system, with applications that go far beyond filtering, in simulation of rare events, simulation of conditioned or constrained random variables, molecular
simulation, etc.
ASPI essentially carries methodological research activities, rather than activities oriented towards a single application area, with the objective of obtaining generic results with high
potential for applications, and of bringing these results (and other results found in the literature) until implementation on a few appropriate examples, through collaboration with industrial
partners.
The main applications currently considered are geolocalisation and tracking of mobile terminals, calibration of models for electricity price, and risk assessment for complex hybrid systems
such as those used in air traffic management.
Scientific Foundations
Monte Carlo methods
Monte Carlo methods are numerical methods that are widely used in situations where (i) a stochastic (usually Markovian) model is given for some underlying process, and (ii) some
quantity of interest should be evaluated, that can be expressed in terms of the expected value of a functional of the process trajectory, which includes as an important special case the
probability that a given event has occurred. Numerous examples can be found, e.g. in financial engineering (pricing of options and derivative securities)
Nof the sample goes to infinity, with rate
 and the asymptotic variance can be estimated using an appropriate central limit theorem. To reduce the asymptotic variance of the estimator, many variance reduction techniques have been
proposed. However, running independent Monte Carlo simulations can lead to very poor results, because trajectories are generated
blindly, and only afterwards are the corresponding weights evaluated. Some of the weights can happen to be negligible, in which case the corresponding trajectories are not going to
contribute to the estimator, i.e. computing power has been wasted.
and the asymptotic variance can be estimated using an appropriate central limit theorem. To reduce the asymptotic variance of the estimator, many variance reduction techniques have been
proposed. However, running independent Monte Carlo simulations can lead to very poor results, because trajectories are generated
blindly, and only afterwards are the corresponding weights evaluated. Some of the weights can happen to be negligible, in which case the corresponding trajectories are not going to
contribute to the estimator, i.e. computing power has been wasted.
A recent and major breakthrough, a brief mathematical presentation of which is given in
explorethe state space under the effect of a
mutationmechanism which mimics the evolution of the underlying process,
and are
replicatedor
terminated, under the effect of a
selectionmechanism which automatically concentrates the particles, i.e. the available computing power, into regions of interest of the state space.
In full generality, the underlying process is a discrete–time Markov chain, whose state space can be finite, continuous (Euclidean), hybrid (continuous / discrete), graphical,
constrained, time varying, pathwise, etc., the only condition being that it can easily be
simulated. The very important case of a sampled continuous–time Markov process, e.g. the solution of a stochastic differential equation driven by a Wiener process or a more general Lévy
process, is also covered.
In the special case of particle filtering, originally developed within the tracking community, the algorithms yield a numerical approximation of the optimal filter, i.e. of the conditional
probability distribution of the hidden state given the past observations, as a (possibly weighted) empirical probability distribution of the system of particles. In its simplest version,
introduced in several different scientific communities under the name of
interacting particle filter
Particle methods are currently being used in many scientific and engineering areas : positioning, navigation, and tracking
Particle methods are very easy to implement, since it is sufficient in principle to simulate independent trajectories of the underlying process. The whole problematic is multidisciplinary,
not only because of the already mentioned diversity of the scientific and engineering areas in which particle methods are used, but also because of the diversity of the scientific communities
which have contributed to establish the foundations of the field : target tracking, interacting particle systems, empirical processes, genetic algorithms (GA), hidden Markov models and
nonlinear filtering, Bayesian statistics, Markov chain Monte Carlo (MCMC) methods.
General framework : Particle approximations of Feynman–Kac flows
The following abstract point of view, developed and extensively studied by Pierre Del Moral
![Im2 ${\#9001 \#956 _n,f\#9002 =\mfrac {\#9001 \#947 _n,f\#9002 }{\#9001 \#947 _n,1\#9002 }~{\mtext and}~\#9001 \#947 _n,f\#9002 ={\#120124 [f(}X_n{)~}\#8719 _{k=0}^ng_k{(}X_k{)]~,}}$](math_image_2.png)
where
Xndenotes a Markov chain with (possibly) time dependent state spaces
Enand with transition kernels
Qn, and where the nonnegative potential functions
gnplay the role of selection functions. Feynman–Kac flows naturally arise whenever importance sampling is used : this applies for instance to simulation of rare events, to filtering,
i.e. to state estimation in hidden Markov models (HMM), etc. Clearly, the unnormalized linear flow satisfies the dynamical system

with the nonnegative kernel
 , and the associated normalized nonlinear flow of probability distributions satisfies the dynamical system
, and the associated normalized nonlinear flow of probability distributions satisfies the dynamical system

which can be decomposed in the following two steps

Conversely, the normalizing constant
 , hence the unnormalized (linear) flow as well, can be expressed in terms of the normalized (nonlinear) flow : indeed
, hence the unnormalized (linear) flow as well, can be expressed in terms of the normalized (nonlinear) flow : indeed
 . To solve these equations
numerically, and in view of the basic assumption that it is easy to
simulater.v.'s according to the probability distributions
. To solve these equations
numerically, and in view of the basic assumption that it is easy to
simulater.v.'s according to the probability distributions
 , i.e. to mimic the evolution of the Markov chain, the original idea behind particle methods consists of looking for an approximation of the probability distribution
, i.e. to mimic the evolution of the Markov chain, the original idea behind particle methods consists of looking for an approximation of the probability distribution
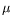
nin the form of a (possibly weighted) empirical probability distribution associated with a system of particles :

The approximation is completely characterized by the set
 of particle positions and weights, and the algorithm is completely described by the mechanism which builds
of particle positions and weights, and the algorithm is completely described by the mechanism which builds
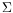
kfrom
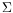
k-1. In practice, in the simplest version of the algorithm, known as the
bootstrapalgorithm, particles
are selected according to their respective weights (selection step),
move according to the Markov kernel
Qk(mutation step),
are weighted by evaluating the fitness function
gk(weighting step).
The algorithm yields a numerical approximation of the probability distribution
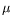
nas the weighted empirical probability distribution
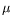
nNassociated with a system of particles, and many asymptotic results have been proved as the number
Nof particles (sample size) goes to infinity, using techniques coming from applied probability (interacting particle systems, empirical processes
 , convergence as empirical processes indexed by classes of functions, uniform convergence in time (see also
, convergence as empirical processes indexed by classes of functions, uniform convergence in time (see also
in the redistribution step, sampling with replacement could be replaced with other redistribution schemes so as to reduce the variance (this issue has also been addressed in genetic
algorithms),
to reduce the variance and to save computational effort, it is often a good idea not to redistribute the particles at each time step, but only when the weights
 are too much uneven.
are too much uneven.
Most of the results proved in the literature assume that particles are redistributed (i) at each time step, and (ii) using sampling with replacement. Studying systematically the
impact of these algorithmic variations on the convergence results is still to be done. Even with interacting Monte Carlo methods, it could happen that some particle
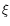
kigenerated in one time step has a negligible weight
gk(
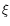
ki) : if this happens for too many particles in the sample
 , then computer power has been wasted, and it has been suggested to use importance sampling again in the mutation step, i.e. to let particles explore the state space under the action of
an alternate wrong mutation kernel, and to weight the particles according to their likelihood for the true model, so as to compensate for the wrong modeling. More specifically, using an
arbitrary importance decomposition
, then computer power has been wasted, and it has been suggested to use importance sampling again in the mutation step, i.e. to let particles explore the state space under the action of
an alternate wrong mutation kernel, and to weight the particles according to their likelihood for the true model, so as to compensate for the wrong modeling. More specifically, using an
arbitrary importance decomposition

results in the following general algorithm, known as the
sampling with importance resampling(SIR) algorithm, in which particles
are selected according to their respective weights (selection step),
move according to the importance Markov kernel
Pk(mutation step),
are weighted by evaluating the importance weight function
Wkon the resulting transition (weighting step).
Statistics of HMM
hidden Markov model (HMM)
asymptotic statistics
local asymptotic normality (LAN)
exponential forgetting
exponential stability
Hidden Markov models (HMM) form a special case of partially observed stochastic dynamical systems, in which the state of a Markov process (in discrete or continuous time, with finite or
continuous state space) should be estimated from noisy observations. The conditional probability distribution of the hidden state given past observations is a well–known example of a normalized
(nonlinear) Feynman–Kac flow, see
Beyond the recursive estimation of a hidden state from noisy observations, the problem arises of statistical inference of HMM with general state space, including estimation of model
parameters, early monitoring and diagnosis of small changes in model parameters, etc.
Large time asymptotics A fruitful approach is the asymptotic study, when the observation time increases to infinity, of an extended Markov chain, whose state includes
(i) the hidden state, (ii) the observation, (iii) the prediction filter (i.e. the conditional probability distribution of the hidden state given observations at all previous time
instants), and possibly (iv) the derivative of the prediction filter with respect to the parameter. Indeed, it is easy to express the log–likelihood function, the conditional least–squares
criterion, and many other clasical contrast processes, as well as their derivatives with respect to the parameter, as additive functionals of the extended Markov chain.
The following general approach has been proposed :
first, prove an exponential stability property (i.e. an exponential forgetting property of the initial condition) of the prediction filter and its derivative, for a misspecified
model,
from this, deduce a geometric ergodicity property and the existence of a unique invariant probability distribution for the extended Markov chain, hence a law of large numbers and a
central limit theorem for a large class of contrast processes and their derivatives, and a local asymptotic normality property,
finally, obtain the consistency (i.e. the convergence to the set of minima of the associated contrast function), and the asymptotic normality of a large class of minimum contrast
estimators.
This programme has been completed in the case of a finite state space
Small noise asymptotics Another asymptotic approach can also be used, where it is rather easy to obtain interesting explicit results, in terms close to the language of
nonlinear deterministic control theory
The following results have been obtained using this approach :
the consistency of the maximum likelihood estimator (i.e. the convergence to the set
Mof global minima of the Kullback–Leibler divergence), has been obtained using large deviations techniques, with an analytical approach
if the abovementioned set
Mdoes not reduce to the true parameter value, i.e. if the model is not identifiable, it is still possible to describe precisely the asymptotic behavior of the
estimators
rof the Fisher information matrix
 is constant in a neighborhood of the set
is constant in a neighborhood of the set
M, then this set is a differentiable submanifold of codimension
r, (ii) the posterior probability distribution of the parameter converges to a random probability distribution in the limit, supported by the manifold
M, absolutely continuous w.r.t. the Lebesgue measure on
M, with an explicit expression for the density, and (iii) the posterior probability distribution of the suitably normalized difference between the parameter and
its projection on the manifold
M, converges to a mixture of Gaussian probability distributions on the normal spaces to the manifold
M, which generalized the usual asymptotic normality property,
it has been shown in
 , in terms of the Kalman filter associated with the linear tangent linear Gaussian model, and (ii) the score function (i.e. the derivative of the log–likelihood function w.r.t.
the parameter), evaluated at the true value of the parameter and suitably normalized, converges to a Gaussian r.v. with zero mean and covariance matrix
, in terms of the Kalman filter associated with the linear tangent linear Gaussian model, and (ii) the score function (i.e. the derivative of the log–likelihood function w.r.t.
the parameter), evaluated at the true value of the parameter and suitably normalized, converges to a Gaussian r.v. with zero mean and covariance matrix
 .
.
New Results
Rare event simulation by MCMC in trajectory space
Frédéric
Cérou
Arnaud
Guyader
Valentine
Méar
Julia
Charrier
rare event
Metropolis–Hastings dynamics
population Monte–Carlo
The estimation of rare event probabilities is a crucial issue in areas such as reliability, telecommunication networks, air traffic management, etc. In complex systems, analytical methods
cannot be used, and naive Monte Carlo methods are clearly unefficient to estimate accurately probabilities of order less than
10
-9, say. Beside importance sampling, a widespread technique is multilevel splitting, which requires at least some knowledge of the system, to decide where to place the
intermediate level sets. In both cases, we need to have some knowledge of the process to find a good set of parameters to run the algotirhm. Moreover, in the case of a rare event to happen
before some deterministic final time, we also need the transient behavior of the process, even if it is ergidic. But usually this transient behavior is very difficult to characterize.
To circumvent these difficulties, we have adopted a completly different approach. We assume that the process is in discrete time, such that a trajectory up to final time
Tis a vector of some finite dimensional space, and we propose to use MCMC approaches to simulate trajectories, given the rare event. Basically, when a proposed transition
in the trajectory space is out of a given set, then it is rejected with probability 1. In this very preliminary work, the plain Metropolis–Hastings algorithm showed inefficient because of
the large dimension of the state space, but some population Monte Carlo variants showed large improvements. The main difficulty here is to built an efficient Metropolis–like algorithm in very
large dimension.
Particle approximations of Feynman–Kac distributions depending on a parameter
François
Le Gland
hidden Markov model (HMM)
Monte Carlo maximum likelihood (MCML)
This is a collaboration with Nadia Oudjane, from the OSIRIS (Optimisation, simulation, risque et statistiques) department of Électricité de France R&D.
In full generality, given nonnegative kernels
 and a nonnegative measure
and a nonnegative measure
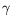 0, we consider the unnormalized (linear) Feynman–Kac distribution
0, we consider the unnormalized (linear) Feynman–Kac distribution

A well–known example is provided by the unnormalized conditional probability distribution of the hidden state given past observations, when the hidden state and the
observation form jointly a Markov chain : this includes HMM and switching AR models as special cases, with the decomposition
 where
where
Qkis the Markov transition kernel and where the selection function
gkis the likelihood function.
If the nonnegative kernels depend on a parameter, in such a way that the Feynman–Kac distribution is continuous or differentiable w.r.t. the parameter, we would like to design a particle
approximation that would have the same regularity properties. The need for such a regularity property arises for instance
in sensitivity analysis, e.g. in the computation of Greeks, in option pricing,
in statistics of HMM, see
The smooth particle approximation introduced earlier has been further studied, where a unique interacting particle system is propagated for a given reference value of the parameter, and
where importance weights are computed separately for each value of the parameter in a neighborhood of the reference value. Differentiating these importance weights w.r.t. the parameter yields a
particle approximation of the linear tangent Feynman–Kac distribution, which coincides with an earlier approach followed in the team, where a particle approximation is derived directly from the
linear tangent Feynman–Kac flow. The new results obtained this year for the joint particle approximation of the Feynman–Kac distribution and the linear tangent Feynman–Kac distribution are
a central limit theorem,
uniform
 error estimates over a neighborhood of the reference value of the parameter,
error estimates over a neighborhood of the reference value of the parameter,
using an original and promising technique where the importance weights are incorporated into the state variable. A Rao–Blackwellized version of the particle approximation has also been
studied, when the underlying state–space model is conditionnally linear Gaussian.
Sequential data assimilation : ensemble Kalman filter vs. particle filter
François
Le Gland
Vu Duc
Tran
data assimilation
ensemble Kalman filter (EnKF)
Our first step has been to better understand on simple examples
This preliminary work has motivated our current interest to study the asymptotic behaviour of the ensemble Kalman filter, as the number of ensemble elements increases to infinity. Indeed,
very little is known about this question, whereas on the other hand, the asymptotic behaviour of the many different brands of particle filters, as the number of particles goes to infinity, is
well understood.
Monte Carlo methods for Bayesian inference
Fabien
Campillo
Vivien
Rossi
Bayesian estimation
Markov chain Monte Carlo (MCMC)
Metropolis-Hastings
particle methods
interacting Monte Carlo methods
Markov chain Monte Carlo (MCMC) algorithms
 known up to a multiplicative constant. They consist in sequentially simulating a single Markov chain whose limit distribution is
known up to a multiplicative constant. They consist in sequentially simulating a single Markov chain whose limit distribution is
 . There exist many techniques to speed up the convergence towards the target distribution by improving the mixing properties of the chain.
. There exist many techniques to speed up the convergence towards the target distribution by improving the mixing properties of the chain.
An alternative is to run many Markov chains in parallel. The simplest multiple chains algorithm is to make use of parallel independent chains. The recommendations concerning this idea seem
contradictory in the literature, as shown by the
many short runs vs. one long rundebate. We can note that independent parallel chains could be a poor idea: among these chains some may not converge, so one long chain could be preferable
to many short ones. Moreover, many parallel independent chains can artificially exhibit a more robust behavior which does not correspond to a real convergence of the algorithm.
In practice one however makes use of several chains in parallel. It is then tempting to exchange information between these chains to improve mixing properties of the MCMC samplers. A general
framework of population Monte Carlo has been proposed in this context
In the present work
Bayesian inference for renewable resources models
Philippe
Cantet
Fabien
Campillo
Vivien
Rossi
Rivo
Rakotozafy
Ricker model
fishery models
Bayesian estimation
Markov chain Monte Carlo (MCMC)
Metropolis within Hastings
interacting Monte Carlo methods
The approach proposed in
Convolution filter based methods for parameter estimation in general state-space models
Fabien
Campillo
Vivien
Rossi
Bayesian estimation
convolution particle methods
Consider a hidden Markov model depending on an unknown parameter. The goal is to estimate simultaneously the parameter and the state process based on the observations. In the Bayesian
approach, the augmented state variable includes the parameter and is processed by a filtering procedure. These methods suppose that a prior law is given for the parameter and are performed
on–line. It is well known that the standard bootstrap particle filter exhibits degenerate behavior in this situation. In
Other Grants and Activities
Data assimilation for air quality (ADOQA) — ARC INRIA
Fabien
Campillo
François
Le Gland
Vu Duc
Tran
January 2005/December 2006.
This ARC is coordinated by the project–team CLIME from INRIA Rocquencourt and CEREA / ENPC. Its partners are the project–team IDOPT from INRIA Rhône–Alpes, and INERIS.
One objective of
[ADOQA]is to investigate
advanced sequential methods (as opposed to variational methods) for data assimilation of intrinsically nonlinear models, i.e. coupling of numerical models and measured data. In principle, a
data assimilation algorithm should propagate uncertainties through the probability distribution of the state variables, whereas current sequential algorithms, such as the Kalman filter and its
simplest extensions, only propagate the first two moments. For large–scale systems (physical state of the atmosphere, of the ocean, chemical composition of the atmosphere, etc.), the direct
implementation of sequential Monte Carlo methods seems impractical, and simplified, reduced–order models should be used.
Our contribution has been to better understand and compare on simple examples
Monte Carlo methods for rare event simulation (RARE) — ARC INRIA
Frédéric
Cérou
Pierre
Del Moral
François
Le Gland
Arnaud
Guyader
January 2006/December 200R.
This ARC is coordinated by the project–team ARMOR from IRISA / INRIA Rennes. The academic partners are the project–team MATHFI of INRIA Rocquencourt and CERMICS / ENPC, the
project–team OMEGA of INRIA Sophia Antipolis and INRIA Lorraine, the project–team MESCAL of INRIA Rhône–Alpes, and the industrial partners are Électricité de France RD, and CENA / DGAC,
and its international partners are CWI (Netherlands) and University of Bamberg (Germany).
The objective of
[RARE]is to design and evaluate
various Monte Carlo techniques (importance sampling, importance splitting, cross–entropy, etc.), for the simulation of rare but critical events, in several important domain of applications
(communication networks, financial risk management, air traffic management, etc.).
Our contribution has been to better understand the asymptotic behaviour of importance splitting methods
It appears that importance splitting can be interpreted in terms of Feynman–Kac distributions, which makes it possible not only to approximate the probability of the rare but critical event,
but also to learn which critical trajectories are responsible for the critical event to occur
Another idea would be to use here the concept of adaptive redistribution, routinely used in particle filtering, without any clear mathematical justification : independent trajectories
would be simulated, as long as an appropriate criterion (interpreted as the normalisation constant in the Feynman–Kac formulation) remains below a given threshold, and would be
replicated / terminated when the monitored criterion would exceed this threshold.
SARIMA and SARIMA–Madagascar
Fabien
Campillo
See
Within the SARIMA program, Fabien Campillo develops collaborations with the universities of Antananarivo and Fianarantsoa in the field of the probabilistic modeling and the numerical
statistical inference for environmental sciences and development. Within this program, Rivo Rakotozafy spend three months per year (one month and a half in 2006) within ASPI in order to prepare
an HDR (habilitation à diriger les recherches) under the supervision of Fabien Campillo. The HDR defense is planed for 2008. The results of this collaboration have been presented to the CARI
conference in Cotonou
Dissemination
Scientific animation
F. Campillo is a member of the committee for the PhD thesis of Ghislain Verdier (École Nationale Supérieure Agronomique de Montpellier and INRA, advisor : Jean–Pierre Vila). He is
a member of the «conseil de laboratoire» of IRISA (UMR 6074) and of the «conseil de l'école doctorale de physique, modélisation et sciences pour l'ingénieur de Marseille». He is the INRIA
representative for scientific relations with Madagascar, within the SARIMA (support to research activities in computer science and mathematics in Africa) project supported by INRIA and MAE
(ministère des affaires étrangères), see
P. Del Moral has organized an invited session on particle methods applied to engineering and physics at the «Journées du groupe MAS» held in Lille in September 2006.
A. Guyader is the coordinator of a reading group at université de Rennes 2, on functional data analysis.
F. Le Gland has reported on the PhD theses of Jaroslav Krystul (Twente University, advisor : Arun Bagchi) and Agnès Lagnoux (université Paul Sabatier, Toulouse,
advisors : Dominique Bakry and Pascal Lezaud). He is a member of the committee for the PhD theses of Olivier Rabaste (université de Rennes 1 and ENST Bretagne, advisor : Thierry
Chonavel) and Anne Cuzol (université de Rennes 1 and IRISA, advisor : Étienne Mémin), and a member of the committe for the HDR (habilitation à diriger les recherches) of Bruno Tuffin
(université de Rennes 1). He has organized an invited session on particle filtering at the XXVI European Meeting of Statisticians held in Toruń in July 2006.
A. Guyader and F. Le Gland are members of the «commission de spécialistes» in applied mathematics (section 26) of université de Rennes 2.
Teaching
F. Campillo gives a course on Markov models, hidden Markov models, filtering and particle filtering at université de Sud Toulon–Var, within the Master «Mathématiques (Filtrage et
traitement des données)» and the Master «Sciences et Technologies (Sciences de la mer, environnement, systèmes)».
F. Le Gland gives a course on Kalman filtering, particle filtering and hidden Markov models, at université de Rennes 1, within the Master STI (école doctorale MATISSE), a 3rd
year course on Bayesian filtering and particle approximation, at ENSTA, Paris, within the quantitative finance track, and a 3rd year course on hidden Markov models, at ENST Bretagne, Brest.
Participation in workshops, seminars, lectures, etc.
Several members of ASPI have given talks in the IRMAR working group on Feynman–Kac formulæ : F. Campillo about particle filtering in practice, F. Le Gland about examples
of applications of Feynman–Kac formulæ, and A. Guyader about Feynman–Kac Metropolis algorithms.
In addition to presentations with a publication in the proceedings, and which are listed at the end of the document, members of ASPI have also given the following presentations.
F. Campillo has given talks on Bayesian inference for renewable resource models in the «Statistiques» seminar at ENSAI in March 2006, and in the «Modèles Statistiques à
Structure(s) Cachée(s)» seminar at Institut de Modélisation et Mathématique in Montpellier, in October 2006. He has presented the joint work on convolution particle filtering for parameter
estimation in general state–space models at the 45th IEEE Conference on Decision and Control (CDC), held in San Diego in December 2006. He has given seminars about Bayesian inference in
environemental sciences in the University of Antananarivo and the University of Fianarantsao, Madagascar, in November 2006.
F. Cérou has given a talk on adaptive multilevel splitting for rare event analysis at the ARC RARE (Monte Carlo methods for rare event analysis) kick–off meeting at IRISA in
April 2006, see
A. Guyader has given talks on adaptive multilevel splitting for rare event analysis at the «Probabilités et Statistiques» seminar of université de Nice–Sophia Antipolis in
April 2006, at the workshop on sequential Monte Carlo methods organized in Oxford in July 2006, at the «Journées du groupe MAS de la SMAI» held in Lille in September 2006, and at
the «Probabilités et Statistiques» seminar of université de Lille 1 in December 2006. He has given a talk on nearest neighbor classification in infinite dimension at the «4èmes
Journées de Statistique Fonctionnelle et Opératorielle» held in Grenoble in June 2006.
F. Le Gland has given talks on the multilevel splitting approach to rare event simulation at the ARC RARE (Monte Carlo methods for rare event analysis) kick–off meeting at IRISA in
April 2006, see
Visits and invitations
F. Campillo has been invited in July and September 2006 in the UMR «Analyse des Systèmes et Biométrie» (ASB) at INRA Montpellier. He has spent three weeks in Madagascar in November
and December 2006 for the SARIMA project, see
F. Le Gland has been invited in November 2006 by Anastasia Papavasiliou in the Department of Statistics of the University of Warwick, and has given there a talk in the CRiSM
(Centre for Research in Statistical Methodology) seminar on adapting the number of particles in Monte Carlo methods with interaction.
Sacha Veretennikov, professor in the Department of Statistics of the University of Leeds has visited ASPI for two days in March 2006, and has given a talk on discrete time ergodic
filters with wrong initial data.
Josselin Garnier, professor at université de Paris 7 has been invited by ASPI in June 2006 to give a talk on rare event simulation.
Pavel Chigansky, post–doc in the Department of Mathematics of Université du Maine has visited ASPI for two days in November 2006, and has given a talk on the stability of the Bayesian
optimal filter with respect to its initial condition.
Rivo Rakotozafy, assistant professor at the University of Fianaranstoa, has been awarded by the French embassy in Antananarivo, Madagascar a grant to support visits to prepare an HDR
(habilitation à diriger les recherches) in Madagascar, under the supervision of Fabien Campillo. A related objective is to set up a collaboration between the University of Fianaranstoa and
INRIA.
![]() and the asymptotic variance can be estimated using an appropriate central limit theorem. To reduce the asymptotic variance of the estimator, many variance reduction techniques have been
proposed. However, running independent Monte Carlo simulations can lead to very poor results, because trajectories are generated
blindly, and only afterwards are the corresponding weights evaluated. Some of the weights can happen to be negligible, in which case the corresponding trajectories are not going to
contribute to the estimator, i.e. computing power has been wasted.
and the asymptotic variance can be estimated using an appropriate central limit theorem. To reduce the asymptotic variance of the estimator, many variance reduction techniques have been
proposed. However, running independent Monte Carlo simulations can lead to very poor results, because trajectories are generated
blindly, and only afterwards are the corresponding weights evaluated. Some of the weights can happen to be negligible, in which case the corresponding trajectories are not going to
contribute to the estimator, i.e. computing power has been wasted.![]()
![]()
![]() , and the associated normalized nonlinear flow of probability distributions satisfies the dynamical system
, and the associated normalized nonlinear flow of probability distributions satisfies the dynamical system![]()
![]()
![]() , hence the unnormalized (linear) flow as well, can be expressed in terms of the normalized (nonlinear) flow : indeed
, hence the unnormalized (linear) flow as well, can be expressed in terms of the normalized (nonlinear) flow : indeed
![]() . To solve these equations
numerically, and in view of the basic assumption that it is easy to
simulater.v.'s according to the probability distributions
. To solve these equations
numerically, and in view of the basic assumption that it is easy to
simulater.v.'s according to the probability distributions
![]() , i.e. to mimic the evolution of the Markov chain, the original idea behind particle methods consists of looking for an approximation of the probability distribution
, i.e. to mimic the evolution of the Markov chain, the original idea behind particle methods consists of looking for an approximation of the probability distribution
![]()
![]()
![]() of particle positions and weights, and the algorithm is completely described by the mechanism which builds
of particle positions and weights, and the algorithm is completely described by the mechanism which builds
![]()
![]()
![]()
![]()
![]() , convergence as empirical processes indexed by classes of functions, uniform convergence in time (see also
,
), central limit theorem (see also
), propagation of chaos, large deviations
principle, moderate deviations principle (see
), etc. Beyond the simplest
bootstrapversion of the algorithm, many algorithmic variations have been proposed
, and are commonly used in practice :
, convergence as empirical processes indexed by classes of functions, uniform convergence in time (see also
,
), central limit theorem (see also
), propagation of chaos, large deviations
principle, moderate deviations principle (see
), etc. Beyond the simplest
bootstrapversion of the algorithm, many algorithmic variations have been proposed
, and are commonly used in practice :![]() are too much uneven.
are too much uneven.![]()
![]()
![]() , then computer power has been wasted, and it has been suggested to use importance sampling again in the mutation step, i.e. to let particles explore the state space under the action of
an alternate wrong mutation kernel, and to weight the particles according to their likelihood for the true model, so as to compensate for the wrong modeling. More specifically, using an
arbitrary importance decomposition
, then computer power has been wasted, and it has been suggested to use importance sampling again in the mutation step, i.e. to let particles explore the state space under the action of
an alternate wrong mutation kernel, and to weight the particles according to their likelihood for the true model, so as to compensate for the wrong modeling. More specifically, using an
arbitrary importance decomposition![]()
![]() is constant in a neighborhood of the set
is constant in a neighborhood of the set
![]() , in terms of the Kalman filter associated with the linear tangent linear Gaussian model, and (ii) the score function (i.e. the derivative of the log–likelihood function w.r.t.
the parameter), evaluated at the true value of the parameter and suitably normalized, converges to a Gaussian r.v. with zero mean and covariance matrix
, in terms of the Kalman filter associated with the linear tangent linear Gaussian model, and (ii) the score function (i.e. the derivative of the log–likelihood function w.r.t.
the parameter), evaluated at the true value of the parameter and suitably normalized, converges to a Gaussian r.v. with zero mean and covariance matrix
![]() .
.