Software
Maple package
diffalg
Evelyne
Hubert
Nonlinear differential systems
differential elimination
analysis of singular solutions
differential algebra
triangulation-decomposition algorithms
The
diffalgis a library that has been part of the commercial release of Maple since Maple V.5 (with an initial version by F. Boulier) and has been developed up to Maple 7 by
E. Hubert. The library implements a triangulation-decomposition algorithm for polynomially nonlinear systems and tools for the analysis of singular solutions. Newer releases are available
on the web (
[
http://www.inria.fr/cafe/Evelyne.Hubert/diffalg]) together with an extensive set of examples of applications and an efficiency test suite. Recent developments include optimized treatment
of parameters, improvements for higher degree equations and generalization to non-commuting derivations.
Library
OreModules
Alban
Quadrat
correspondent
Daniel
Robertz
Constructive algebraic analysis
constructive homological algebra
Ore algebras
Gröbner bases
linear functional systems
control theory
mathematical physics
The
OreModulespackage of Ore
-algebra (Ore
-algebra is a part of the commercial release of Maple) is dedicated to the algebraic study of linear systems of functional equations defined over some Ore algebras (e.g., ordinary or
partial differential equations, time-delay equations, difference equations) and their applications in mathematical physics (e.g., research of potentials, computations of field equations and
conservation laws) and in linear control theory (e.g., parameterizability, flatness, autonomous elements, first integrals of motion, equivalences, controllability, observability, input-output
behaviour).
The main novelty of
OreModulesis to combine the recent developments of the Gröbner bases over some Ore algebras (non-commutative polynomial rings) with new algorithms of
algebraic analysis in order to effectively check classical properties of module theory (e.g., existence of a non-trivial torsion submodule, torsion-freeness, reflexiveness, projectiveness,
stably freeness, freeness), give their system-theoretical interpretations (existence of autonomous elements or successive parametrizations, existence of minimal/injective parametrizations,
Bézout equations or generalized inverses) and compute important tools of homological algebra (e.g., (minimal) free resolutions, splitting, extension functor, projective dimension, Hilbert power
series).
The main advantage of the language of homological algebra used in
A library of more than 30 examples coming from engineering sciences and mathematical physics (e.g., a two pendulum mounted on a car, a wind tunnel model, stirred tank
models, a two reflector antenna, an electric transmission line, linearized Einstein equations, Maxwell equations, linear elasticity, Lie-Poisson structures) illustrates the main functions and
applications of
OreModules.
Library
Stafford
Alban
Quadrat
correspondent
Daniel
Robertz
Stafford theorems
bases of free modules over the Weyl algebras
generators of ideals over the Weyl algebras
computation of flat outputs
block-diagonalization and block-triangularization problems
The
Staffordpackage of
OreModulescontains an implementation of constructive versions of the J. T. Stafford's famous but tricky theorem stating that every ideal
over the Weyl algebras
 and
and
 of differential operators with polynomial and rational coefficients can be generated by two generators. Based on this implementation and on algorithmic results recently obtained by the
authors of this package, two algorithms have been implemented which compute bases of free modules over the Weyl algebras
of differential operators with polynomial and rational coefficients can be generated by two generators. Based on this implementation and on algorithmic results recently obtained by the
authors of this package, two algorithms have been implemented which compute bases of free modules over the Weyl algebras
 and
and
 .
.
The development of the
Staffordpackage was mainly motivated by the wish to compute flat outputs of flat multidimensional linear systems with varying coefficients, a problem
appearing in control theory. However, it has recently played an important role in the decomposition problem of linear systems of partial differential equations with polynomial or rational
coefficients. For more details, see Section
Library
Morphisms
Thomas
Cluzeau
Alban
Quadrat
correspondent
Factorization and decomposition of linear functional systems
constructive homological algebra
quadratic first integrals
quadratic conservation laws
algebraic analysis
The forthcoming
Morphismspackage of
OreModuleswas developed in order to constructively handle some homological tools such as computations of morphisms between two finitely presented
modules over Ore algebras, compute kernel, coimage, image and cokernel of morphisms and projectors of the ring of endomorphisms. Using the packages
Stafford(see Section
In terms of module theory, the
Morphismspackage gives some methods to test if two modules are isomorphic, if a given module contains a submodule (reducible modules) or if it can be
written as the direct sum of two submodules. Applications of the
Morphismspackage to mathematical physics and control theory are illustrated in a library of examples (e.g., computation of Galois symmetries of
physical systems, quadratic first integral and conservation laws, decomposition of linear systems coming from mathematical physics and control theory, equivalence of systems).
Library
QuillenSuslin
Anna
Fabiańska
Alban
Quadrat
correspondent
Quillen-Suslin theorem
flat multidimensional systems
Lin-Bose conjecture
(weakly) doubly factorization
block-diagonalization and block-triangularization problems
The forthcoming
QuillenSuslinpackage of
OreModules, developed by A. Fabiańska (University of Aachen) with the help of A. Quadrat, contains an implementation of the famous
Quillen-Suslin theorem. In particular, this implementation allows us to compute bases of free modules over a commutative polynomial ring with coefficients in a field (mainly
 ) and in a principal ideal domain (mainly
) and in a principal ideal domain (mainly
 ). The development of this package was led by different applications of the Quillen-Suslin theorem in multidimensional systems theory (e.g., computation of flat outputs of flat
multidimensional systems, equivalence problems, Lin-Bose conjecture, computation of (weakly) doubly coprime factorizations) and signal processing (e.g., parametrization of synthesis filters).
Finally, it has recently played a crucial role in the decomposition problem of linear systems of partial differential equations with constant coefficients (see Section
). The development of this package was led by different applications of the Quillen-Suslin theorem in multidimensional systems theory (e.g., computation of flat outputs of flat
multidimensional systems, equivalence problems, Lin-Bose conjecture, computation of (weakly) doubly coprime factorizations) and signal processing (e.g., parametrization of synthesis filters).
Finally, it has recently played a crucial role in the decomposition problem of linear systems of partial differential equations with constant coefficients (see Section
Library
libaldor
Manuel
Bronstein
Aldor
standard
data structures
arithmetic
The
[libaldorlibrary], under development in the project for several years, became the standard
Aldorlibrary, bundled with the compiler distribution since 2001.
Library
Algebra
Manuel
Bronstein
Marc
Moreno-Maza
University of Western Ontario
Computer algebra
linear algebra
commutative algebra
polynomials
The
[Algebralibrary], written in collaboration with Marc Moreno-Maza, is now also bundled with the
Aldorcompiler, starting with version 1.0.2, which has been released in May 2004. It is intended to become a standard core for computer algebra
applications written in
Aldor.
Library
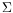 i t
Manuel
Bronstein
Computer algebra
differential equations
difference equations
systems
i t
Manuel
Bronstein
Computer algebra
differential equations
difference equations
systems
The
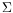 i tlibrary
i tlibrary[http://www-sop.inria.fr/cafe/Manuel.Bronstein/sumit/bernina_demo.html]that has solved third order equations as well since the end of 2004.
New Results
Fast algorithms for linear differential and difference equations
Thomas
Cluzeau
Alin
Bostan
ALGO project
Frédéric
Chyzak
ALGO project
Bruno
Salvy
ALGO project
Linear differential and difference equations
polynomial and rational solutions
complexity
binary splitting
baby step-giant step
indefinite and definite summation
The search for rational (and thus polynomial) solutions of linear differential and difference equations lies at the heart of several important algorithms in computer algebra.
In
We then address the problem of computing rational solutions. The compact representation of polynomial solutions of linear differential equations also allows us to
evaluate, in quasi-optimal complexity, their value and that of their derivatives at a rational or algebraic point. We can also perform divisions by high powers of a monomial which lead directly
to an algorithm in quasi-optimal complexity to compute rational solutions of linear differential equations.
This year, we have continued our joint work by looking at the case of difference equations. The calculation of polynomial solutions works in the same way except that the
coefficients of these polynomials satisfy a linear recurrence equation in the binomial basis instead of the monomial basis. The generalization of our techniques for computing rational solutions
is a little bit more difficult because of the appearance of a new phenomenon called the dispersion. However, binary splitting and baby step/giant step techniques together with the compact
representation of the numerator allow us to obtain an algorithm in quasi-optimal complexity. As a direct consequence, we obtained fast versions of Abramov's algorithm computing rational
solutions of linear recurrence equations, Gosper's algorithm for indefinite summation, and Zeilberger's algorithm for definite summation. Our algorithms have been implemented in Maple. This
work has been published in
Formal solutions of partial differential systems at a singular point
Nicolas
Le Roux
Moulay
Barkatou
University of Limoges
Evelyne
Hubert
Pfaffian systems
normal crossings singularities
regular and irregular singularity
Completely integrable systems are well studied. They are encountered for instance in isomonodromic deformations or in differential geometry. We consider here completely integrable systems
with normal crossings singularities. These systems can be rewritten locally in the form

The
Aiare
m×
mmatrices with entries in the ring
![Im18 ${{\#8450 [[}x_1,...,x_n{]]}}$](math_image_18.png) and the
and the
piare non negative integers.
Yis a
m×1vector of unknowns with coordinates in an extension of
 .
.
We investigate algorithms for the computation of formal solutions of completely integrable systems with normal crossing singularities. We expect to extend the known
algorithms for ordinary differential systems.
As in the ordinary case, there are three kinds of singularities at the origin. Singularities of the
first kindare those for which
pi= 0for all
i. Every system of the first kind is equivalent, by a transformation
Y=
TZwith
 , to a system where the matrices have constant entries
, to a system where the matrices have constant entries
mth stage. Stabilization at the
mth stage, not appearing in van den Essen criterion, is of main interest for algorithmic purposes.
For singularities of the first kind the solution space can be described in terms of the monodromy matrices. More precisely, one can find a basis of solutions

where
![Im22 ${T\#8712 M_m{(\#8450 [[}x_1,...,x_n{]])}}$](math_image_22.png) with
det(
with
det(
T)
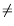 0and the
0and the
C(
i)s are
m×
mconstant matrices commuting with one another. We obtained
The description of the solution space at regular singularities is then obtained if we have the transformation that reduces the system to a system of the first kind.
For irregular singularities, H. Charrière was the first to describe the solution space in the case where the system only involves two independent variables
Our first goal is to provide an algorithm for reducing the order of the singulatrity at the origin - that is the length of
(
p
1, ...,
p
n)- by linear transformations. Such a reduction process would allow us to decide wether or not the singularity is regular. We have investigated the possibility to extend Moser's
algorithm
n= 2
n= 2, we are building an algorithm for computing a basis of formal solution for systems with irregular singularities, relying on the rank reduction algorithm
previously proposed. This is to be written in a forthcoming paper.
For
n>2, the difficulties we encounter are twofold. Firstly, the systems considered are not invariant under transformation
Y=
TZ. Secondly, there is no warranty that the lattices are free. The same problem arose in
Factorization and decomposition of linear functional systems
Cluzeau
Thomas
Alban
Quadrat
Factorization and decomposition of linear functional systems
constructive homological algebra
quadratic first integrals
quadratic conservation laws
algebraic analysis
The factorization and decomposition problems of systems of linear ordinary differential or difference equations have long been studied in the mathematical and symbolic computation
literatures
Following ideas of M. F. Singer
D-module
M, finitely presented by a matrix
Rwith entries in an Ore algebra
D, to a left
D-module
Npresented by a matrix
S. If
Dis a commutative ring or
Mand
Nare two finite-dimensional
k-vector spaces (e.g., case of ordinary differential systems or integrable connections), then we can effectively compute the set
h o m
D(
M,
N)of morphisms from
Mto
N. If the previous hypotheses are not fulfilled, then we can only compute the set of morphisms of a given order. A morphism from
Mto
Ndefines a transformation sending a solution of the system
Sz= 0into a solution of
Ry= 0. When
S=
R, the ring
e n d
D(
M)of the endomorphisms of
Mcorresponds to the ``Galois symmetries'' of the system
Ry= 0. Moreover, we have explicitly characterized the kernel, coimage, image and cokernel of a morphism from
Mto
N, a fact that can be used to check the equivalence of the systems
Ry= 0and
Sz= 0.
We have proved that the existence of a non-injective endomorphism of a left
D-module
M, finitely presented by a matrix
Rwith entries in an Ore algebra
D, corresponded to a factorization of the form
R=
R1R2, where
R1and
R2are two matrices with entries in
D. Using this result, we have shown how the integration of the system
Ry= 0could be done by means of a cascade of integrations. Moreover, we have described how to compute the projectors of
e n d
D(
M)and proved that they allowed us to decompose the system
Ry= 0into two decoupled systems
Q1y1= 0and
Q2y2= 0, where
Q1and
Q2were two matrices with entries in
D. Hence, the integration of the system
Ry= 0becomes equivalent to the integrations of the two independent systems
Q1y1= 0and
Q2y2= 0. Then, under certain conditions on the projectors (freeness), we proved that the system
Ry= 0was equivalent to a block diagonal system. In particular, these conditions always hold in the case of a univariate Ore algebra over a field of coefficients (i.e.,
ordinary differential/difference systems over the field of rational functions) and in the case of a multivariate commutative Ore algebras due to the Quillen-Suslin theorem (e.g., linear system
of partial differential equations with constant coefficients) (see Section
An(
k)and
Bn(
k)over a field
kof characteristic 0 (i.e., linear system of partial differential equations with polynomial/rational coefficients over
k) (see Section
Ry= 0when it exists. For all the previous results, no condition on the system
Ry= 0is required such as
D-finite, determined, underdetermined, overdetermined, i.e., this approach handles general linear systems over an Ore algebra. In the case of a finite-dimensional
determined system over an Ore algebra with rational coefficients, we find again the results obtained in M. Wu's PhD thesis
The different algorithms have been implemented in the package
Morphisms(see Section
Linear systems over Ore algebras and applications
Alban
Quadrat
Daniel
Robertz
Constructive algebraic analysis
constructive homological algebra
Ore algebras
Gröbner bases
linear functional systems
control theory
mathematical physics
In the publications
 -free... The problem of parameterizing the solutions of multidimensional linear systems has been extensively studied in control theory by the school of M. Fliess and
J. C. Willems. Our results allow us to effectively answer that problem for classes of functional systems. The different algorithms obtained in
-free... The problem of parameterizing the solutions of multidimensional linear systems has been extensively studied in control theory by the school of M. Fliess and
J. C. Willems. Our results allow us to effectively answer that problem for classes of functional systems. The different algorithms obtained in
The purpose of
Finally, we have shown in
Applications of the Stafford theorems and implementation
Alban
Quadrat
Daniel
Robertz
Aachen University
Stafford theorems
bases of free modules over the Weyl algebras
generators of ideals over the Weyl algebras
computation of flat outputs
block-diagonalization and block-triangularization problems
It is quite well-known that an analytic time-varying controllable ordinary differential system is
flatoutside some singularities
A well-known and difficult result due to J. T. Stafford asserts that a stably free left module
Mover the Weyl algebras
D=
An(
k)or
Bn(
k)of differential operators with polynomial/rational coefficients
-where
kis a field of characteristic 0
-with
r a n k
D(
M)
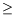 2is free. The purpose of
2is free. The purpose of
M. This algorithm, based on the new constructive proofs
D, performs Gaussian eliminations on the columns of the formal adjoint of the presentation matrix of
M. Moreover, we show that J. T. Stafford's result is a particular case of a more general one asserting that a stably free left
D-module
Mwith
r a n k
D(
M)
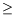 s r (
s r (
R)is free, where
s r (
R)denotes the stable range of a ring
D. This result is constructive if the stability of unimodular vectors with entries in
Dcan be tested. An algorithm which computes the left projective dimension of a general left
D-module
Mdefined by means of a finite free resolution is presented. In particular, it allows us to check constructively whether or not the left
D-module
Mis stably free. All these algorithms have recently been implemented in the package
Stafford(see Section
Dand a basis of any free left
D-module.
These results can be used in order to recognize whether or not a linear system of ordinary/partial differential equations with polynomial/rational coefficients admits an
injective parametrization. This problem is interesting in the theory of flat systems
Applications of the Quillen-Suslin theorem and implementation
Anna
Fabiańska
Aachen University
Alban
Quadrat
Quillen-Suslin theorem
flat multidimensional systems
differential time-delay systems
Lin-Bose conjecture
(weakly) doubly factorization
block-diagonalization and block-triangularization problems
In 1955, a famous conjecture due to Serre asserted that if we take a row vector
vwith coefficients in a commutative polynomial ring
A=
k[
x1, ...,
xn](
kis a field) which admits a right-inverse over
A, then
vcan be embedded into a square unimodular matrix, namely, a matrix with a non-zero constant determinant. This conjecture was proved independently by Quillen and Suslin in
1976 and is nowadays called the Quillen-Suslin theorem. In terms of module theory, Serre's conjecture means that a projective
A-module is free and the computation of the unimodular matrix then gives an explicit basis for this module. Constructive proofs of the Quillen-Suslin theorem have been
largely studied in the literature of constructive algebra (e.g., see
A-modules in
OreModules. This project has recently been finished by A. Fabiańska (University of Aachen, Germany) within the framework of her PhD thesis
supervised by Prof. W. Plesken with the help of A. Quadrat. A package called
QuillenSuslinwill be soon available (see Section
The Quillen-Suslin theorem has many applications in mathematical systems theory and signal processing and, in particular, it allows us to constructively compute flat
outputs of flat or
 -flat shift-invariant multidimensional linear systems such as time-invariant differential time-delay control systems. Hence, the present work gives the first implementation for the
computation of flat outputs of flat shift-invariant multidimensional linear systems
-flat shift-invariant multidimensional linear systems such as time-invariant differential time-delay control systems. Hence, the present work gives the first implementation for the
computation of flat outputs of flat shift-invariant multidimensional linear systems
Moreover, using a constructive version of the Quillen-Suslin theorem, A. Fabiańska and A. Quadrat show in
Resolvent representation for systems of ordinary differential equations
Thomas
Cluzeau
Evelyne
Hubert
Differential algebra
resolvent representation
triangulation-decomposition algorithms
We had previously shown
Algebraic and differential Invariants
Evelyne
Hubert
Irina
Kogan
North Carolina State University
Alexandre
Sedoglavic
University of Lille
Eric
Schost
Ecole Polytechnique, University of Western Ontario
Algebraic invariants
differential invariants
Lie groups
algebraic groups
cross-section
In
[
http://www.inria.fr/cafe/Evelyne.Hubert/aida]). In
An essential property of the algebraic invariants we consider is that the field they generate is isomorphic to the field of rational functions on a given cross-section to
the orbits. Their algebraic structure is therefore simple and is the basis for determining the differential algebraic structure of the differential invariants. We have made some progress on the
determination of this differential algebra.
A particularly favorable case is when the cross-section intersects generic orbits only once, in which case we say the cross-section is of degree one. Such cross-sections
are known to exist for
specialgroups
Invariants are the natural objects to translate algebraically the geometry and symmetry of problems in diverse fields of science. They allow to reduce the dimension of
problems by factoring out the symmetry. We applied those ideas for the nondimensionalisation of dynamical systems. Reducing the number of parameters in biological models retaining the
qualitative properties of the dynamics has often been considered an art
Algebraic analysis approach to infinite-dimensional linear systems
Alban
Quadrat
Infinite-dimensional systems
analysis and synthesis problems
internal/strong/simultaneous/robust/optimal stabilization
parametrization of all the stabilizing controllers
algebraic analysis
Until today, no one has seemed to be able to algebraically incorporate the initial and limit conditions of a system of partial differential equations within the differential module approach
(
D-modules). From analytical and engineering points of view, the algebraic
D-module approach is not yet totally satisfactory. Driven by applied questions arising in control theory, A. Quadrat has tried to develop a new algebraic analysis
approach which could solve this negative point for a class of linear systems of partial differential equations depending on two or three independent variables (typically, one independent
variable is the time variable and one or two independent variables are the space variables) usually encountered in engineering sciences. This class of systems is usually called
infinite-dimensional linear systems
Using
symbolic analysis, also called
symbolic calculus, developed by O. Heaviside, P. Dirac and L. Schwartz, i.e., techniques based on Laplace transform, convolution products, distributions and symbolic
integration (special functions), we can transform an infinite-dimensional linear system into a transfer matrix, i.e., into functional relations between the state and the outputs of the system
and its inputs and initial conditions. The transfer matrix carries important information of the system and particularly its stability (e.g., unstable poles correspond to unstable modes).
Combining natural functional algebras, which were introduced for studying the stability of the systems, and the fractional representation approach to systems
Using the algebraic concepts of lattices, we have shown in the publications
 era parametrization of all stabilizing controllers for multi-input multi-ouput systems which do not necessarily admit coprime factorizations. The Youla-Ku
era parametrization of all stabilizing controllers for multi-input multi-ouput systems which do not necessarily admit coprime factorizations. The Youla-Ku
 era parametrization has been the cornerstone of the success of the
era parametrization has been the cornerstone of the success of the
 -control in the recent years as this parametrization allows us to rewrite the problem of finding the optimal stabilizing controllers (for a certain norm) as affine, and thus, convex
problems.
-control in the recent years as this parametrization allows us to rewrite the problem of finding the optimal stabilizing controllers (for a certain norm) as affine, and thus, convex
problems.
Finally, the algebraic analysis techniques also allowed us to positively solve in the publication
![]() , i.e. the left-hand side of differential equations where the right-hand side is zero, is the largest set of differential polynomials that vanish on the solution set of
, i.e. the left-hand side of differential equations where the right-hand side is zero, is the largest set of differential polynomials that vanish on the solution set of
![]() . This is the object that our algorithms manipulate and for which we compute adequate representations in order to answer the above questions.
. This is the object that our algorithms manipulate and for which we compute adequate representations in order to answer the above questions.![]() , the system can be defined by means of matrices with entries in non-commutative algebras of functional operators such as differential operators, shift operators, time-delay
operators... An important class of operators algebras is called
Ore algebrasand was introduced in
.
, the system can be defined by means of matrices with entries in non-commutative algebras of functional operators such as differential operators, shift operators, time-delay
operators... An important class of operators algebras is called
Ore algebrasand was introduced in
.![]()
![]() (
(
![]() (
(
![]() with
with
![]() , i.e.
, i.e.![]()
![]() of
of
![]() :
:![]()
![]() is the projection. The system of
is the projection. The system of
![]() is the image of the fundamental group
is the image of the fundamental group
![]() 1(
1(
![]() ,
,
![]() obtained in the process of continuation of the local solutions defined in a neighbourhood of
obtained in the process of continuation of the local solutions defined in a neighbourhood of
![]() .
.![]() has a rational first integral. Ziglin found a necessary condition for the existence of a maximal number of first integrals (without involutivity property) for analytic Hamiltonian
systems, when
has a rational first integral. Ziglin found a necessary condition for the existence of a maximal number of first integrals (without involutivity property) for analytic Hamiltonian
systems, when
![]() . If the Hamiltonian system with
. If the Hamiltonian system with
![]() , then any other monodromy matrix
, then any other monodromy matrix
![]() transforms eigenvectors of
transforms eigenvectors of
![]() by the differential Galois group
by the differential Galois group
![]() of the NVEs. They formulated
a new criterion of non-integrability for
Hamiltonian systems in terms of the properties of the connected identity component of
of the NVEs. They formulated
a new criterion of non-integrability for
Hamiltonian systems in terms of the properties of the connected identity component of
![]() : if a Hamiltonian system is meromorphically integrable in the Liouville sense in a neighbourhood of the analytic curve
: if a Hamiltonian system is meromorphically integrable in the Liouville sense in a neighbourhood of the analytic curve
![]() , then the identity component of the differential Galois group of NVEs associated with
, then the identity component of the differential Galois group of NVEs associated with
![]() is Abelian.
is Abelian.![]() always contains
always contains
![]() , the Morales-Ramis non-integrability theorem always yields stronger necessary conditions than the Ziglin criterion.
, the Morales-Ramis non-integrability theorem always yields stronger necessary conditions than the Ziglin criterion.![]() is Abelian, a task where the tools of algorithmic Galois theory (such has the Kovacic algorithm) become useful. In practice, we often check only whether that component is solvable
(which is equivalent to check whether the NVEs have Liouvillian solutions), because the system is not integrable when that component is not solvable.
is Abelian, a task where the tools of algorithmic Galois theory (such has the Kovacic algorithm) become useful. In practice, we often check only whether that component is solvable
(which is equivalent to check whether the NVEs have Liouvillian solutions), because the system is not integrable when that component is not solvable.