Rewriting
rewriting
strategies
types
rewriting calculus
conditional rewriting
We have developed the foundational study of the rewriting calculus, studied the combination of conditional rewriting with lambda-calculus and continued to study probabilistic rewrite
systems.
Explicit
 -calculus
Horatiu
Cirstea
Germain
Faure
Claude
Kirchner
-calculus
Horatiu
Cirstea
Germain
Faure
Claude
Kirchner
Following the works on explicit substitutions for
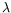 -calculus, we proposed, studied and exemplified
-calculus, we proposed, studied and exemplified
 -calculus that handles explicitly the resolution of the matching constraints and the application of the obtained substitutions. We have also shown that the approach is modular and we
have introduced a calculus handling explicitly only the substitution application and another one where the matching constraints are solved at the object level while the resulting
substitutions are applied at the meta-level
-calculus that handles explicitly the resolution of the matching constraints and the application of the obtained substitutions. We have also shown that the approach is modular and we
have introduced a calculus handling explicitly only the substitution application and another one where the matching constraints are solved at the object level while the resulting
substitutions are applied at the meta-level
The explicit substitution application studied initially
Moreover, in this approach the matching constraints with no solution can be eliminated earlier in the reduction process leading to a more efficient evaluation. This can be achieved by
integrating in the explicit calculus the approach already used for the plain calculus
Graphs in the
 -calculus
Clara
Bertolissi
Horatiu
Cirstea
Claude
Kirchner
-calculus
Clara
Bertolissi
Horatiu
Cirstea
Claude
Kirchner
Starting from the classical untyped
 -calculus and in collaboration with Paolo Baldan from the University of Venice, we have proposed an extension of the calculus, called
graph rewriting calculus, handling structures containing sharing and cycles, rather than simple terms
-calculus and in collaboration with Paolo Baldan from the University of Venice, we have proposed an extension of the calculus, called
graph rewriting calculus, handling structures containing sharing and cycles, rather than simple terms
The classical
 -calculus is naturally generalized by considering lists of constraints containing unification constraints in addition to the standard matching constraints. This leads to a term-graph
representation in an equational style where terms consist of unordered lists of constraints. As for the classical
-calculus is naturally generalized by considering lists of constraints containing unification constraints in addition to the standard matching constraints. This leads to a term-graph
representation in an equational style where terms consist of unordered lists of constraints. As for the classical
 -calculus, the transformations are performed by explicit application of rewrite rules as first class entities.
-calculus, the transformations are performed by explicit application of rewrite rules as first class entities.
The evaluation rules are adapted to the new syntax leading to an enhanced expressive power for the calculus. In this new formalism we can represent and manipulate elaborated objects like,
for example, regular infinite entities.
Several aspects of the calculus have been investigated so far, like its properties (we have also shown that the calculus is confluent over equivalence classes of terms, under some
linearity restrictions on patterns) and its relationship with other existing frameworks
 -calculus and a version of the
-calculus and a version of the
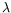 -calculus extended with a
letreclike construct. Moreover, the possibility of representing structures with cycles and sharing
-calculus extended with a
letreclike construct. Moreover, the possibility of representing structures with cycles and sharing
 -Calculus and Combinatory Reduction Systems
Clara
Bertolissi
Horatiu
Cirstea
Claude
Kirchner
-Calculus and Combinatory Reduction Systems
Clara
Bertolissi
Horatiu
Cirstea
Claude
Kirchner
Since
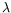 -calculus and rewriting have complementary features, their combination has been studied in different contexts. We have already shown that
-calculus and rewriting have complementary features, their combination has been studied in different contexts. We have already shown that
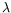 -calculus and rewriting are generalized by the
-calculus and rewriting are generalized by the
 -calculus, in the sense that the syntax and the inference rules of the
-calculus, in the sense that the syntax and the inference rules of the
 -calculus can be restricted to obtain the other two formalisms.
-calculus can be restricted to obtain the other two formalisms.
In the prolongation of our works on the expressive power of the
 -calculus we have analyzed the relation between
-calculus we have analyzed the relation between
 -calculus and higher order rewriting. We gave a precise definition of the matching in Combinatory Reduction Systems (
CRS)
-calculus and higher order rewriting. We gave a precise definition of the matching in Combinatory Reduction Systems (
CRS)
 -calculus
-calculus
 -calculus
-calculus
We have also addressed the converse issue: how to simulate rewriting calculus derivations by Combinatory Reduction Systems ones. As a consequence of this result, important properties, like
standardisation, are deduced for the rewriting calculus
Distributive rewriting calculus
Horatiu
Cirstea
Clément
Houtmann
Benjamin
Wack
General term rewriting systems and classical guiding strategies have been encoded in the original rewriting calculus
We have shown recently that the previously proposed encoding can be extended to the general case,
i.e. to arbitrary term rewrite systems
Implementation techniques for the Rewriting Calculus
Horatiu
Cirstea
Germain
Faure
We used the
 -calculus as an intermediate language to compile functional languages with pattern-matching features, and adapt the evaluation strategies developed for the
-calculus as an intermediate language to compile functional languages with pattern-matching features, and adapt the evaluation strategies developed for the
 -calculus to the specific constraints arising from typed functional programs.
-calculus to the specific constraints arising from typed functional programs.
In
 -calculus in interaction nets
-calculus in interaction nets
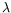 -calculus). We showed
-calculus). We showed
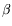 -reduction can proceed in parallel, without additional overheads. The compilation of functional programs in the
-reduction can proceed in parallel, without additional overheads. The compilation of functional programs in the
 -calculus, and the subsequent interaction net encoding, uncover a new strategy of evaluation which naturally exploits the implicit parallelism of the different rules of the calculus.
This methodology gives thus rise to new, efficient strategies of evaluation for functional languages.
-calculus, and the subsequent interaction net encoding, uncover a new strategy of evaluation which naturally exploits the implicit parallelism of the different rules of the calculus.
This methodology gives thus rise to new, efficient strategies of evaluation for functional languages.
Canonical sets of terms
Horatiu
Cirstea
Germain
Faure
Claude
Kirchner
Term collections are fundamental in the context of the rewriting calculus but also in logic programming and in web query languages. Typically, matching constraints that are involved in the
calculus may have more than one solution (this is also the case for example in programming language like TOM, Maude, ASF+SDF or ELAN) and thus generates a collection of results.
As a first step in the study of the rewriting calculus with non-unitary matching theories, we studied the lambda-calculus with term collections
In the spirit of the normalized rewriting
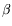 -rule is an explicit evaluation step. While the work of
-rule is an explicit evaluation step. While the work of
Matching modulo superdeveloppements
Germain
Faure
Claude
Kirchner
We are interested in the optimization of rewrite based programs and since the
 -calculus can be used to encode such programs, a promising approach seems to be based on the matching modulo
-calculus can be used to encode such programs, a promising approach seems to be based on the matching modulo
 -reduction.
-reduction.
Higher-order matching has been already used
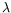 -terms and solved them modulo superdevelopments
-terms and solved them modulo superdevelopments
A next step consists in defining the notions of developments and superdevelopments in the context of the
 -calculus and adapt the proposed algorithms for this case.
-calculus and adapt the proposed algorithms for this case.
Rewriting and probabilities
Olivier
Bournez
Florent
Garnier
Claude
Kirchner
Last year, in a papier published in RTA, we introduced the notion of probabilistic rewrite systems and we gave some conditions entailing termination of those systems within a finite mean
number of reduction steps.
Termination was considered under arbitrary unrestricted policies. Policies correspond to strategies for non-probabilistic rewrite systems.
This is often natural or more useful to restrict policies to a subclass. This year, in paper
Polygraphs and functional programming
Yves
Guiraud
Frédéric
Blanqui
Albert Burroni's polygraphs
The main objective is to start the realization of a computer environment, called Cat, for the construction and study of low-dimensional polygraphs, such as the ones encountered in
rewriting, functional programming and proof theory. Its main purpose is to bolster both theoretical studies and new applications, which will be, in turn, integrated into Cat.
Among such applications, a use of polygraphs in complexity analysis is currently examined together with Guillaume Bonfante (Calligramme, INRIA Lorraine). The usual setting of functional
programming, term rewriting, is not adaptated for the study of the complexity of "divide and conquer"-like algorithms, such as the "fast sort", using polynomial termination orders. But
polygraphs provide a more natural description of these programs and allow one to recover the complexity of the ``fast sort'' using simple polynomial interpretations, whose theory is already
known
The same kind of interpretations can also be used to prove termination of term rewriting systems which are not simply terminating, yielding a new possible technique for automatically
proving termination. With Frédéric Blanqui, the termination tools of Cat will be adaptated for use on the Termination Problems Data Base to check the power of this new method.
Finally, fundations are also studied with Albert Burroni and François Métayer (Preuves-Programmes-Systèmes, Paris 7), mainly to polygraphically understand binding operators such as the
abstraction of the
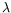 -calculus or the quantifiers of first-order logic, possibly leading to a new generation of explicit substitutions calculi. Working sessions with Jean-Louis Loday (Institut de Recherche
Mathématique Avancée de Strasbourg, CNRS) and Philippe Malbos (Institut Camille Jordan, Lyon 1) are programmed to continue to develop the transfer of rewriting techniques in universal algebra
and homology theory.
-calculus or the quantifiers of first-order logic, possibly leading to a new generation of explicit substitutions calculi. Working sessions with Jean-Louis Loday (Institut de Recherche
Mathématique Avancée de Strasbourg, CNRS) and Philippe Malbos (Institut Camille Jordan, Lyon 1) are programmed to continue to develop the transfer of rewriting techniques in universal algebra
and homology theory.
Rule based programming
algebraic specification
abstract data-types
pattern matching
compilation
We are studying the design and the implementation of rule based programming languages. We are interested in modularizing our technologies in order to make them available as separate
elementary tools.
Also, we continue our study on the application of rule based languages. In particular, we study their applications to XML transformations as well as the analysis and the certification of
program transformations.
Quotient types in functional programming
Frédéric
Blanqui
In the Modulogic project of the ACI Sécurité Informatique, we are developing with Pierre Weis (project Cristal, INRIA Rocquencourt) and Thérèse Hardin (LIP6, Paris), a program generation
tool, called Moca, that produces construction functions for quotient types in OCaml. Quotient types are types whose values represent equivalence classes modulo some equational theory.
Invariants like ``the list is sorted'', ``there is no element occuring twice'', ...can be seen as quotient types modulo common algebraic equational theories like commutativity, idempotence,
...Generating construction functions for ensuring such invariants may be difficult. Consider for instance the combination of associativity (for having right combs) and idempotence for a
binary constructor
C. Building the representive of the equivalence class of
C(
x,
y)when both
xand
yare the representatives of their equivalence class, requires to test a number of patterns proportional to the size of
y. For instance,
C(
x,
C(
y,
C(
x,
y)))must be represented by
C(
x,
y). We are already able to generate construction functions for some combinations of such theories
Formal Island
Émilie
Balland
Claude
Kirchner
Pierre-Etienne
Moreau
Antoine
Reilles
Anderson
Santana
In
Our first work has been to formalize the relations between the algebraic terms and the concrete objects representing them. Since
Tomis data-structure independent, we needed a formal view of the mapping mechanism used in
Tom, defining a general framework allowing to anchor algebraic pattern-matching capabilities in existing languages like C, Java or ML. This provides a specific instance of what we call
a formal island. Then, using a powerful enough intermediate language, which could be viewed as a subset of
C
Java
ML, we formalized the behavior of compiled code and defined the correctness of compiled code with respect to pattern-matching behavior. This allowed us to prove the equivalence of
compiled code correctness with a generic first-order proposition whose proof could be achieved via a proof assistant or an automated theorem prover. We worked with Damien Doligiez from the
Cristal project on how to connect our tool with the Zenon theorem prover, and how to help the theorem prover proving these goals. We then extended these results to the multi-match situation
characteristic of the ML like languages. The approach has been implemented on top of the
Tomcompiler, and used to validate some syntactic matching construction. This prototype implementation will be extended to support full multi-match constructions and to automatize the
cooperation with Zenon.
Anti-Pattern Matching
Claude
Kirchner
Radu
Kopetz
Pierre-Etienne
Moreau
Pattern matching is a concept widely spread both in computer science community and in everyday life. Whenever we search for something, we build a structured object, a pattern, that
specifies the features we are interested in. But we are often in the case where we want to exclude certain characteristics: typically we would like to specify that we search for white cars
that are not station wagons.
To this end, we have defined in
Strategic Programming in Java
Émilie
Balland
Pierre-Etienne
Moreau
Antoine
Reilles
We have defined a new formalism
As imagined several years ago, a sophisticated strategy language is needed to control the application of rules and describe complex exploration strategies. Inspired by Stratego, we have
defined a strategy language for
Tom. Starting from elementary strategies such as identity, failure, sequence, congruence, and recursion. More elaborated strategies such repeat, top-down or innermost can be defined.
Recently we have defined and implemented a strategy library where the strategy expressions can be parameterized, matched, dynamically rewritten, and explored by strategies itself. Written in
Java, in some sense this brings functions to the object level. The presented strategy language has been applied to the development of verification tools
The strategy language has also been used to specify an optimizer for
Tom. We have introduced a program transformation phase, presented in
Rewriting-Based Access Control Policies
Anderson
Santana
Claude
Kirchner
Hélène
Kirchner
Recently we proposed a formalization of access control policies based on term rewriting
Rule-Based Modeling for Biochemical Applications
Oana
Andrei
Hélène
Kirchner
Transformations in chemical systems are naturally expressed by rules on some classes of graphs. The work on rule-based programming using
ELANfor the automated generation of chemical reactions involved in combustion reaction mechanisms, presented in
The rule-based approach on graph structures has also been studied in the domains of biological systems and protein interactions. This motivated us in starting to develop a rewriting
calculus based on
 -calculus for modelling the interactions in biochemical systems using a graph-like representation for the biochemical species. The control of biochemical reaction applications can then
be expressed by means of strategies as it was already done for the control of chemical reactions.
-calculus for modelling the interactions in biochemical systems using a graph-like representation for the biochemical species. The control of biochemical reaction applications can then
be expressed by means of strategies as it was already done for the control of chemical reactions.
Mechanized deduction
deduction modulo
decision procedures
constrained theories
induction proofs
equational proofs
completion procedures
termination
We continued to develop both the inductive and size-based approaches to termination of rule-based programs. We also began to develop a
Coqlibrary for certifying termination proofs. Finally, we developed the use of ``good proofs'' in automated deduction.
Inductive strong termination proofs
Isabelle
Gnaedig
Hélène
Kirchner
In previous works, we have proposed a method for specifically proving, by explicit induction, termination of rewriting under strategies. The proof principle consists, for a given term
rewriting system, in establishing on the ground term algebra that every term terminates i.e. has only finite derivations, assuming that any smaller term terminates. For that, we developed
proof trees representing the possible derivations from any term using the term rewriting system. Two mechanisms are used, namely abstraction, introducing variables that represent ground terms
in normal form and schematize normalization of subterms, and narrowing, schematizing rewriting in different ways according to the ground instances it represents. These two mechanisms deal
with constraints used to control the growth of the proof trees.
After applying this methodology for proving termination of rewriting with the innermost, the outermost and the local strategies, we worked on a factorization of these three procedures, and
obtained a generic algorithm with appropriate instances to the different strategies.
This year, we completed this work in studying the ordering constraints generated by our inductive proof principle, in order to automate the proof algorithms for the different strategies.
For the three rewriting strategies, we have analyzed the behavior of our approach on the examples of the TPDB termination data base
[
http://www.lri.fr/~marche/tpdb/]. Thanks to the power of induction, for most examples, the subterm ordering or a lexicographic path ordering are sufficient. Else, a polynomial ordering can verify the constraints.
We identified and analyzed other failure cases for ordering constraint solving and proposed a few solutions. This work has been submitted to a journal
Sufficient completeness and termination
Isabelle
Gnaedig
Hélène
Kirchner
By its generality, the principle of the inductive method, we have proposed for termination, is promising to handle other properties. So we have studied the possibility to prove sufficient
completeness with our approach.
This led us to generalize the well-known result linking sufficient completeness and ground reducibility, in establishing that only weak termination suffices for the second property to
imply the first. Moreover, sufficient completeness usually applies to a set of equations, and then extends to a rule-based program if rules are confluent and terminating. Unfortunately,
often, programs do not fulfill the last two requirements. To avoid them, we introduced the notion of C-reducibility, expressing that every data evaluates into a constructor form i.e. a
completely evaluated expression, for at least one of its possible evaluations. We proposed an algorithm, based on our induction principle, using narrowing and abstraction, to establish
C-reducibility, even if the program does not terminate. It is constructive in the sense that a computation branch leading to a constructor form can be deduced from the generated proof trees.
As the most important thing for a program is to give an evaluated form for every data, our result relativizes the importance of termination in the context of programming
Higher-order conditional rewriting
Frédéric
Blanqui
Claude
Kirchner
Colin
Riba
We extended to conditional rewriting the work of Dougherty
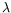 -calculus and algebraic rewriting. We considered the following two cases: when
-calculus and algebraic rewriting. We considered the following two cases: when
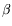 -reduction is used or not in the evaluation of conditions. Incidentally, we improved Dougherty's result by requiring weak normalization of
-reduction is used or not in the evaluation of conditions. Incidentally, we improved Dougherty's result by requiring weak normalization of
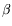 -reduction (
i.e. existence of a terminating
-reduction (
i.e. existence of a terminating
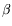 -reduction) instead of strong normalization (
i.e. termination of every
-reduction) instead of strong normalization (
i.e. termination of every
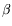 -reduction). Finally, we provided a syntactic condition for ensuring orthogonality, hence confluence, in case of conditions with higher-order terms. This is the first study on the
confluence of
-reduction). Finally, we provided a syntactic condition for ensuring orthogonality, hence confluence, in case of conditions with higher-order terms. This is the first study on the
confluence of
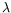 -calculus with higher-order conditional rewriting
-calculus with higher-order conditional rewriting
Size-based termination
Frédéric
Blanqui
Colin
Riba
In previous years, we generalized to rewriting and dependent types the so-called type or size based termination criteria for ML-like function definitions. They are based on the way
inductive types are usually constructed: as fixpoints of monotone operators on the set of terms. The number of steps necessary for reaching a term in such a fixpoint gives a simple and
natural measure, the size, which is finer than the syntactic structure. By enriching the syntax of types with size annotations, one can express that a term has a size (strictly) smaller than
another term.
In
Termination of higher-order rewrite systems
Frédéric
Blanqui
In the first-order case, the termination of a rewrite system
Ris equivalent to the top termination of its dependency pairs modulo
R
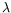 -calculus for some class of rewrite systems by using Tait's technique of computability predicates.
-calculus for some class of rewrite systems by using Tait's technique of computability predicates.
In
Abstract completion
Guillaume
Burel
Claude
Kirchner
Solving goals, like deciding word problems or resolving constraints, is much easier in some theory presentations than in others. What have been called ``completion processes'',
particularly in the study of equational logic, involves finding appropriate presentations of a given theory to solve easily a given class of problems.
We have designed a general proof-theoretic setting within which completion-like processes can be modeled and studied. This framework (the abstract canonical systems and inference) centers
around well-founded orderings of proofs. It allows for abstract definitions and very general characterizations of saturation processes and redundancy criteria
In
In
Super deduction
Horatiu
Cirstea
Paul
Brauner
Clément
Houtman
Claude
Kirchner
Benjamin
Wack
Following the seminal work of Benjamin Wack on extended natural deduction
Induction and rewriting
Claude
Kirchner
Hélène
Kirchner
Fabrice
Nahon
Following our work with Eric Deplagne on a proof theoretic framework to perform rewrite based inductive reasonning
Computability and complexity
complexity
computability
implicit complexity
analog computations
We focus on computational models working over reals with a discrete and continuous time. This year we mainly focused on continuous time models. Concerning continuous time models, we have
provided machine independent characterizations of computable and elementary computable functions over reals. We have also discussed the computational power of several models.
Analog computations
Olivier
Bournez
Daniel
Graça
Emmanuel
Hainry
There are many ways to model analog computers. Unifying those models is therefore a crucial matter as opposed to the discrete case, as there is no property stating that those models are
equivalent. It is possible to distinguish two groups in these models: on one side, continuous time models; on the other side, discrete time models working on continuous structures as a model
derived from Turing machines. The first group contains in particular some sets of functions defined by Moore in
There are few comparisons between classes of functions from the first group and from the second group, and in particular, there were almost no result of equality.
It is known that Euler's Gamma function is computable according to computable analysis, while it cannot be generated by Shannon's General Purpose Analog Computer (GPAC). This example has
often been used in order to argue that the GPAC is less powerful than digital computations.
However, as we demonstrated in
In
Some of the results above are part of the PhD thesis of Emmanuel Hainry. Emmanuel Hainry defended his PhD thesis in December
``Computation on the real numbers can be modelised in several different ways. There indeed exist a lot of different computation models on the reals. However, there exist few results for
comparing those models, and most of these results are incomparability results. The case of computation over the real numbers hence is quite different from that of computation over integer
numbers where Church-Turing's thesis claims that all reasonable models compute exactly the same functions.
The results presented in this document are twofold. One, we show that recursively computable functions (in the sense of computable analysis) can be shown equivalent to some adequately
defined subclass of
 -recursive functions, and also to gpac-computable functions with gpac-computable roughly meaning computable through a converging gpac. Hence we get a machine independent
characterization of recursively computable functions, and a bridge between type 2-machines and gpac. Two, more than an analog characterization of recursively enumerable functions, we show
that the limit operator we defined can be used to provide an analog characterization of elementarily computable functions and
-recursive functions, and also to gpac-computable functions with gpac-computable roughly meaning computable through a converging gpac. Hence we get a machine independent
characterization of recursively computable functions, and a bridge between type 2-machines and gpac. Two, more than an analog characterization of recursively enumerable functions, we show
that the limit operator we defined can be used to provide an analog characterization of elementarily computable functions and
 -computable functions for
-computable functions for
n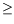 3, where
3, where
 represents the levels of Grzegorczyk's hierarchy.
represents the levels of Grzegorczyk's hierarchy.
Those results can be seen as a first step toward a unification of computable functions over the reals.''
![]() -calculus and rewriting that we called rewriting calculus (
-calculus and rewriting that we called rewriting calculus (
![]() -calculus, for short)
. The notion of
-calculus, for short)
. The notion of
![]() -reduction of the rewriting calculus generalises
-reduction of the rewriting calculus generalises
![]() -reduction by considering matching on patterns which can be more elaborated than simple variables. We have been studying the expressiveness of this general formalism and the properties
of its various instances.
-reduction by considering matching on patterns which can be more elaborated than simple variables. We have been studying the expressiveness of this general formalism and the properties
of its various instances.![]() -calculus, and more generally in rewrite engines.
-calculus, and more generally in rewrite engines.