Linear Algebra
Huge Linear Systems
Huge linear systems are frequently encountered as last steps of ``index-calculus'' based algorithms. Those systems correspond to a particular presentation of the underlying group by
generators and relations; they are thus always defined on a base ring which is
 modulo the exponent of the group, typically
modulo the exponent of the group, typically
 in the case of factorization,
in the case of factorization,
 when trying to solve a discrete logarithm problem over
when trying to solve a discrete logarithm problem over
 .
.
Those systems are often extremely sparse, meaning that they have a very small number of non-zero coefficients.
The classical, naive elimination algorithm of Gauss yields a complexity of
O(
n3), when the matrix considered has size
n×
n. However, if we assume that we can perform a matrix multiplication in time
 , algorithms exist which lower this complexity to
, algorithms exist which lower this complexity to
 . Furthermore, if we make assumptions on our matrix (mainly that it is sparse, meaning that a matrix-vector product can be computed in time
. Furthermore, if we make assumptions on our matrix (mainly that it is sparse, meaning that a matrix-vector product can be computed in time
 for some
for some
 <2), then specialized algorithms (Lanczós, Wiedemann
<2), then specialized algorithms (Lanczós, Wiedemann
 , typically
, typically
O(
n2)for the very sparse matrices (
 = 1) that we often encounter.
= 1) that we often encounter.
Lattices
Many problems described in the other sections, but also numerous problems in computer algebra or algorithmic number theory, involve at some step the solution of a linear problem or the
search for a short linear combination of vectors lying in a finite-dimensional Euclidean space. As examples of this, we could cite factoring and discrete logarithms methods for the former,
finding worst cases for the Table Maker's Dilemma in computer arithmetic for the latter (see Section
The important problem in that setting is, given a ``bad'' basis of a lattice, to find a ``good'' one. By good, we mean that it consists of short, almost orthogonal vectors. This is a
difficult problem in general, since finding the shortest nonzero vector is already NP-hard, under probabilistic reductions.
In 1982, Lenstra, Lenstra, and Lovász
O(
n2log
M)linear algebra steps (of type matrix-vector multiplication), or
O(
n4log
M)operations
O(
nlog
M), therefore giving a
O(
n6log
3M)bit complexity if the underlying arithmetic is naive.
State of the art
Large Linear Systems
Recall that the systems we are dealing with are usually systems with coefficients in a finite ring, which can be either small (
 ), or quite a large ring.
), or quite a large ring.
Lanczós' method
Given a symmetric matrix
Aand a vector
x, Lanczós' method computes, using Gram-Schmidt process, an orthogonal basis
 of the subspace generated by
{
of the subspace generated by
{
x,
A
x,

Anx}for the scalar product
[
x,
y] = (
x|
A
y). As soon as one finds an isotropic vector
wi, i.e.,
[
w
i,
w
i] = 0, one has
witAwi= 0. In our situation, we take
A=
BtB, where we want to find a vector in the kernel of
B; we thus have
(
w
i
B)
t
B
w
i= 0. Over a finite field this does not always imply
Bwi= 0, but this remains true with probability close to 1 over a finite ring of large characteristic. This approach works over
 as well, but with some caution.
as well, but with some caution.
Wiedemann's method
Given a matrix
A(not necessarily symmetric) and a vector
x, Wiedemann's algorithm looks for a trivial linear combination of the vectors
Aix,
i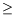 1. Such a relation can be written as
1. Such a relation can be written as
 . Now, if
. Now, if
 is a nonzero vector, we have
is a nonzero vector, we have
Au= 0, and
uis a vector of the kernel of
A. The linear combination, in turn, is searched by choosing a random vector
yand computing the elements
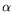
i=
yAix. If a relation of the type we are looking for exists, then
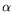
iis a linear recurring sequence of order
n. Given
2
nelements of the sequence, Berlekamp-Massey's algorithm allows one to compute the coefficients of the recurrence. Thus, with
O(
n)matrix-vectors and
O(
n)vector-vector products, one hopes to recover a vector of the kernel. The overall complexity is thus, on average,
 , as announced.
, as announced.
Parallel and distributed algorithms
Algorithms for solving large sparse linear systems have been designed with implementation, and parallelism or distribution in mind, or both. The Lanczós and Wiedemann algorithms have
``block'' versions
The block Wiedemann algorithm has been used by Thomé
 , where
, where
pis a prime of 183 decimal digits. This computation was made feasible using an algorithm based on the Fast Fourier Transform (FFT), which permitted broader
distribution of the computation
Today, block versions of the Lanczós and Wiedemann algorithms are a necessity for who wants to solve linear systems encountered in record-size factoring problems, discrete logarithm
problems, or in some other cases. Yet, a precise account on the positive and negative sides of both block algorithms, and a formulation of their preferred setting, seems to be missing.
Arithmetics
We consider here the following arithmetics: integers, rational numbers, integers modulo a fixed modulus
n, finite fields, floating-point numbers and
p-adic numbers. We can divide those numbers in two classes:
exact numbers(integers, rationals, modular computations or finite fields), and
inexact numbers(floating-point and
p-adic numbers).
Algorithms on integers (respectively floating-point numbers) are very similar to those on polynomials (respectively Taylor or Laurent series). The main objective in that domain is to find
new algorithms that make operations on those numbers more efficient. These new algorithms may use an alternate number representation.
Integers
The integral types of the current processors have a width
wof either 32 or 64 bits. This means that, using hardware instructions, one is only able to compute modulo
2
32or
2
64. An arbitrary precision integer is then usually represented under the form
 , with
, with
nia machine integer. In algorithmic terms, it means that a multiprecision integer is an array of machine integers. Naive operations can then be defined by using the classical
``schoolbook methods'' in base
2
w, with linear complexity in the case of addition and subtraction, and quadratic complexity in the case of division and multiplication.
Integers Modulo
nand Finite Fields
Integers modulo
nare usually represented by the representative of their class in the interval
[0,
n-1]or sometimes
]-
n/2,
n/2].
Addition, subtraction and multiplication are obtained from the corresponding operation over the integers, after reduction modulo
n. This means that after each operation, a reduction modulo
nmust be performed. This is not very costly in the case of addition and subtraction (where it implies a single test and half the time another addition of subtraction),
but implies a division in the case of multiplication.
The modular division is a completely different operation, and amounts to compute a so-called extended gcd of
xand
n, i.e., a pair
a,
bwith
ax+
bn= 1. This is classically performed by the Euclidean algorithm or one of its variants, and is thus, in practice, by far the most costly operation. Many improvements
in low-level algorithms are obtained by choosing suitable representations of objects which avoid divisions modulo
n.
Finite fields can be separated in two types. Prime fields correspond to the integers modulo
nfor prime
n. Extension fields are algebraic extensions of those prime fields, i.e.,
![Im25 ${\#8484 /p\#8484 [X]}$](math_image_25.png) modulo an irreducible polynomial
modulo an irreducible polynomial
P(
X). Elements of a non-prime finite field are thus often represented as polynomials of elements of a prime field. This means that ideas from polynomial arithmetic
can, and should be used.
A difficult case is the case when
pdeg
P(the cardinality of the field) is large whereas neither
pnor
deg
Preally are. The case where
pis large is indeed a classical case where we have to deal with arithmetic with large integers, and fast algorithms exist in that case. The case where
pis small and
deg
Plarge corresponds to the realm of fast polynomial arithmetic. However, in the ``middle range'', neither
pnor
deg
Pare large enough to justify the use of fast techniques. This is also at the core of some technical theoretical difficulties.
p-adic Numbers
A
p-adic number is defined as the formal limit of a sequence
(
x
n)of integers such that
xi=
xi+ 1mod
pi. One could think of it as a formal series
 , with
, with
 , though alternative representations are sometimes more efficient for some computations. In particular, a
, though alternative representations are sometimes more efficient for some computations. In particular, a
p-adic number given to the precision
nis simply an element of
 .
.
The
p-adic numbers offer the capability of lifting information known in a finite field to a field of characteristic zero, keeping some structure information at the same
time. They are extensively used by many algorithms in computer algebra and algorithms related to algebraic curves, together with their extensions.
When we are trying to lift information from a nonprime finite field, say
 for
for
q=
pn, we are led to introduce algebraic extensions of
 ; algebraic extensions of the
; algebraic extensions of the
p-adics can be of two types,
unramified extensionsand
ramified extensions; roughly speaking, ramified extensions contain fractional powers of
p.
In practice, we are mostly interested in the case of small
pand unramified extensions. Of lesser importance are
p-adic integers for large
p, and extensions of these, because the algorithms we have in mind are generally not practical for large
p. Yet, this is not necessarily the case for any possible
p-adic algorithm, hence this point of view may change. At present, our application realms do not call for
p-adic arithmetic requiring computations in ramified extensions, but this may change in the future as well.
Floating-point Numbers and the IEEE-754 Standard
When discussing inexact types, one stumbles very quickly on two critical difficulties:
since approximation is inherent to the manipulation of inexact types, how should approximation be performed? This amounts to defining the (necessarily) finite set of numbers that can
be exactly represented (format),
even if the two operands of an operation can be exactly represented, in general the result cannot be. How should one define the result of an operation (rounding)? This is the key for a
precise and portable semantics of floating-point computations.
From now on, we shall focus on the floating-point numbers, which are the main inexact data type, at least from the practical point of view.
Formats.
A floating-point format is a quadruple
(
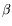 ,
,
n,
E
min,
E
max); a floating-point number in that format is of the form
±(
b
0.
b
1...
b
n-1)·
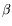
e,
where
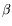 is the
base— usually 2 or 10 —,
is the
base— usually 2 or 10 —,
nis the
significand width,
e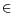 [
[
Emin,
Emax]is the
exponent, and the
biare the
digits,
0
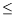
b
i<
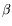 . The IEEE-754 standard defines four binary floating-point formats (single
precision, single-extended, double precision, double-extended), the single-extended format being obsolete:
. The IEEE-754 standard defines four binary floating-point formats (single
precision, single-extended, double precision, double-extended), the single-extended format being obsolete:
| format |
total width |
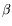
|
significand width |
E
m
i
n
|
E
m
a
x
|
| single |
32 |
2 |
24 |
-126
|
+ 127
|
| double |
64 |
2 |
53 |
-1022
|
+ 1023
|
| double-extended |
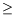 79 79
|
2 |
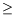 64 64
|
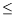 -16382 -16382
|
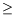 + 16383 + 16383
|
The on-going revision (754r) forgets about the single-extended and double-extended formats, and defines a new quadruple precision format (binary128). It also defines new decimal
formats:
| format |
total width |
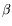
|
significand width |
E
m
i
n
|
E
m
a
x
|
| binary128 |
128 |
2 |
113 |
-16382
|
+ 16383
|
| decimal32 |
32 |
10 |
7 |
-95
|
+ 96
|
| decimal64 |
64 |
10 |
16 |
-383
|
+ 384
|
| decimal128 |
128 |
10 |
34 |
-6143
|
+ 6144
|
Rounding.
The IEEE-754 standard defines four rounding modes: rounding to zero, to
+
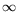 , to
-
, to
-
 , and to nearest-even. It requires that any of the four basic arithmetic
operations (
+ , -, ×, ÷), and the square root, must be
correctly rounded, i.e., the rounded value of
, and to nearest-even. It requires that any of the four basic arithmetic
operations (
+ , -, ×, ÷), and the square root, must be
correctly rounded, i.e., the rounded value of
a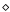
bfor
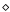
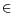 { + , -, ×, ÷}must be the closest one to the exact value (assuming that the
inputs are exact) — as if one were using infinite precision — according to the rounding direction. (In case of an exact result lying exactly in the middle of two consecutive machine
numbers, the nearest-even mode chooses that with an even mantissa, i.e., ending with
{ + , -, ×, ÷}must be the closest one to the exact value (assuming that the
inputs are exact) — as if one were using infinite precision — according to the rounding direction. (In case of an exact result lying exactly in the middle of two consecutive machine
numbers, the nearest-even mode chooses that with an even mantissa, i.e., ending with
bn-1= 0in binary.)
The Table Maker's Dilemma
Let
fbe a mathematical function (for example the exponential, the logarithm, or a trigonometric function), and a given floating-point format
(
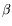 ,
,
n,
E
min,
E
max). Assume
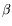 = 2, i.e., a binary format for simplicity. Given a floating-point number
= 2, i.e., a binary format for simplicity. Given a floating-point number
xin that format, we want to determine the floating-point number
yin that format — or in another output format — that is closest to
f(
x)for a given rounding mode. In that case, we say that
 is
correctly rounded. The problem here is that we cannot compute an infinite number of bits of
is
correctly rounded. The problem here is that we cannot compute an infinite number of bits of
f(
x). All we can do is to compute an approximation
zto
f(
x)on
m>
nbits, with an error bounded by one
ulp(unit in last place). Consider for example the arc-tangent function, with the double-precision number
x= 4621447055448553·2
-11, and rounding to nearest. We have in binary:

where the first line contains 53 significant bits, and the second one has 45 consecutive zeros. If
m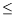 99, we'll get as approximation
99, we'll get as approximation
 , which is exactly the middle of two double-precision numbers, and therefore we will not be able to determine the correct rounding of
arctan
, which is exactly the middle of two double-precision numbers, and therefore we will not be able to determine the correct rounding of
arctan
x. We say that
xis a
worst casefor the
arctanfunction and rounding to nearest. Since a given format contains a finite number of numbers — at most
2
64for double-precision —, the maximal working precision
mrequired for any
xin that format is finite. The Table Maker's Dilemma (TMD for short) consists in determining that maximal working precision
mmaxneeded, which depends on
f, the format and the rounding mode, and possibly the corresponding worst cases
x. Once we know
mmax, we can design an efficient routine to correctly round
fas follows: (i) compute a
mmax-bit approximation
zto
f(
x), with an error of at most one ulp, (ii) round
z.
State of the art
Integers
Most basic algorithms for integers are believed to be optimal, up to constant factors. The main goal here is thus to save on those constant factors. For the multiplication, one challenge
is to find the best algorithm for each input size; since the thresholds between the different algorithms (naive, Karatsuba, Toom-Cook, FFT) are machine-dependent, there is no theoretical
answer to that question. The same holds for the problem of finding which kind of FFT (Mersenne, Fermat, complex, Discrete Weighted Transform or DWT) is the fastest one for a given
application or input size.
For the division, it is well known that it can be performed — as any algebraic operation — in a constant times that of the corresponding multiplication: for example, a
n×
nproduct corresponds to a
(2
n)/
ndivision. One main challenge is to decrease that constant factor, say
d. In the naive (quadratic) range, we have
d= 1, but already in the Karatsuba range, the best known implementation has
d= 2
d= 1, however its implementation seems tricky, and its memory usage is superlinear.)
Floating-point numbers
Algorithms for floating-point numbers make great use from those for integers. Indeed, a binary floating-point number may be represented as an integer significand multiplied by 2
e. Multiplication of two floating-point numbers therefore reduces to the product of their significands; this product is in fact a
short product, since only the high part is needed (assuming all numbers have the same precision). Despite some recent theoretical advances
Integers modulo
n.
A special case of integer division is when the divisor
nis constant. This happens in particular in modular or finite field computations (discrete logarithm and factorization via ECM for instance). There are basically two
kinds of algorithms in that case: (i) Barrett's division
n, which is used to get an approximation to the quotient, which after a second product yields an approximate remainder, (ii) Montgomery's reduction precomputes
-1/
nmod
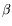
k(where the input
nhas
kwords in base
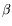 ) which gives in two products the value of
) which gives in two products the value of
c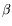 -
-
kmod
n, for
chaving
2
kwords in base
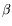 . Both algorithms perform two products with operands of size equal to the size of
. Both algorithms perform two products with operands of size equal to the size of
n. These products are in fact short products, but according to the above remark, the global cost is close to that of two plain products. A speedup can be obtained in
the FFT range, where the second product (to obtain the remainder) produces a known high part (resp. low part) in Barrett's division (resp. Montgomery's reduction); using the fact
that the FFT computes that product modulo
2
m±1, one can save a factor of two for that product, with a global gain of 25%. Together with caching the transform of the input
nand of its approximate inverse, one approaches
d= 1. These ideas still need to be implemented in common multiple-precision software.
p-adic numbers.
Recently, a large number of new ``
p-adic'' algorithms for solving very concrete problems have been designed, notably for counting points on algebraic varieties defined over finite fields. The
application of such algorithms to coding theory or cryptology is immediate, as this is a considerable aid for quickly setting up elliptic curve cryptosystems, or for finding good codes.
Some of these algorithms have been listed in Section
In such algorithms, computations are carried out in ``
p-adic structures'', but this vague wording reflects a relatively wide variety of mathematical structures (not unrelated to the underlying finite field, of course).
We are frequently led to computing in the ring of 2-adic integers, which can be regarded as the integers modulo
2
nfor some variable precision
n. Also, just as extensions of
 are very common in computer algebra in general, the ring of integers of unramified extensions of 2-adic numbers plays an important role.
are very common in computer algebra in general, the ring of integers of unramified extensions of 2-adic numbers plays an important role.
The Table Maker's dilemma.
Some instances of the TMD are easy. For example, for an algebraic function of total degree
d, we get an upper bound of
mmax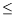
dn+
O(1)
d= 2. Another easy case is the base conversion, where the TMD reduces to
O(
Emax-
Emin)computations of continued fractions
However, in general, and especially for non-algebraic functions, the TMD is a difficult problem, because we know no rigorous upper bound for
m, or the corresponding upper bound is much too large. However, a quick-and-dirty statistical analysis shows that for a
n-bit input format (including the exponent bits if needed), the worst case is about
 . But to determine a rigorous bound, the only known methods are based on exhaustive search. Basically, they compute a
2
. But to determine a rigorous bound, the only known methods are based on exhaustive search. Basically, they compute a
2
n-bit approximation to
f(
x)for every
xin the given format, and see how many consecutive zeros or ones appear after (or from) the round bit. This naive approach has complexity
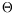 (2
(2
n). Fortunately, faster — but still exponential — methods do exist. The first one is Lefèvre's algorithm
 . An improved algorithm of complexity
. An improved algorithm of complexity
 is given in
is given in
![]() , for various
, for various