Scientific Foundations
Analysis of Algorithms
analysis of algorithms
combinatorial analysis
analytic combinatorics
random discrete structures
index tree
hashing methods
asymptotic enumeration
limit laws
While we know the laws of basic physics and while probabilists have been setting up a coherent theory of stochastic processes for about half a century, the “laws of combinatorics”, in the
sense of the laws governing random structured configurations of large sizes, are much less understood. Accordingly, our knowledge in the latter area is still very much fragmentary. Some of the
difficulties arise from the large variety of models that tend to arise in real-life applications—the world of computer scientists and algorithmic designers is really an artificial world, much
more “free” than its physical counterpart. Some of us have then engaged in the long haul project of trying to offer a unified perspective in this area. The approach of analytic combinatorics
has evolved from there.
Analytic combinatorics leads to discovering randomness phenomena that are “universal” (a term actually borrowed from statistical physics) across seemingly different applications. For
instance, it is found that similar laws govern the behaviour of prime factors in integers, of irreducible factors in polynomials, of cycles in permutations, and of components in mappings of a
finite set. Once detected, such phenomena can then be exploited by specific algorithms that factor integers (a problem relevant to public-key cryptography), decompose polynomials (this is
needed in computer algebra systems), reorganize tables in place (this is of obvious interest in the manipulation of various data sets), and use collisions to estimate the cardinality of massive
data ensembles. The underlying technology bases itself on generating functions, which exactly describe discrete models, as well as an interpretation of these generating functions as analytic
transformations of the complex plane. Singularities together with the associated perturbative theory then deliver a number of very precise estimates regarding important characteristics of
random discrete structures. The process can be largely made formal and accessible to computer algebra (see below) and it may be adapted to the broad area of analysis of algorithms.
Computer Algebra
asymptotic scales
random generation
special functions
Gröbner bases
Computer algebra at large aims at making effective large portions of mathematics, paying due attention to complexity issues. For reasons mentioned above, our project specifically
investigates the way mathematical objects originating in complex analysis can be dealt with in an algorithmic way by computer algebra systems. Our main contributions in this area concern the
automation of asymptotic analysis and the handling of special functions. The mathematical foundations of our algorithms are deeply rooted in differential algebra (Hardy fields for asymptotic
expansions and Ore algebras for special functions).
Over the years, in order to automate the average-case analysis of ever larger classes of algorithms, we have developed algorithms and implementations for the following problems: the
specification of formally specified combinatorial structures; the corresponding problems of enumeration and random generation; the automatic construction of asymptotic scales which is necessary
for extracting the singular behaviour of generating functions; the automatic computation of asymptotic expansions in such scales; the automatic computation of asymptotic expansions satisfied by
coefficients of generating series. An
Encyclopedia of Combinatorial Structures, available on the web, gathers roughly one thousand structures for which generating series, recurrences, and asymptotic behaviour have been
determined automatically using our libraries.
An important principle of computer algebra is that it is often easier to operate with equations defining a mathematical object implicitly rather than trying to obtain a “closed-form”
expression of it. The class of linear differential and difference equations is particularly important in view of the large variety of functions and sequences they capture. In this area, we have
developed the highly successful
gfunpackage (jointly with P. Zimmermann, from the Spaces project) dealing with the univariate case. In the multivariate case, we have developed
the underlying theory based on Gröbner bases in Ore algebra, and an implementation in the
Mgfunpackage. The algorithmic advances of the past few years have made it possible to start the implementation of an
Encyclopedia of Special Functions, providing various information concerning classical functions (of wide use throughout sciences), including Bessel functions, Airy functions, .... The
corresponding information is all automatically generated.
Algorithms on Sequences
combinatorics on words
sequences
pattern matching
genome
The goal of our research on sequences is the design of new algorithms and the computation of their average-case complexity or the derivation of combinatorial results on words and their
implementation in statistical software. Possible applications are data compression and genomic sequences. A new area arises in the context of genomic sequences, where biologically significant
motifs are extracted. This subject combines algorithms searching for potential signals (the candidates), and computations of statistical significance. For each candidate, the choice criterion
is its underrepresentation or overrepresentation. Due to the large number of potential candidates, the speed and the numerical precision of the computation are crucial.
From a methodological point of view, we exhibit several renewal processes, and the limiting law is usually a Gaussian law. Here, the tail distributions are necessary, as one needs to
evaluate the overrepresentation, or the underrepresentation, of a motif. The combinatorial properties of words allow, for this class of problems, an effective computation of formulae valid in
the central domain and in the tails. Asymptotic analysis yields an exact expression of the rate function, in the sense of large deviation theory. Simultaneously, we define for each problems
some characteristic languages in order to bound the computational complexity in the Markovian case.
Software
Software
The
Algoliblibrary is a set of Maple routines that have been developed in the project for more than 10 years. Several parts of it have been incorporated into the standard library of Maple,
but the most up-to-date version is always available for free from our web pages. This library provides: tools for combinatorial structures (the
combstructpackage), this includes enumeration, random or exhaustive generation, generating functions for a large class of attribute grammars; tools for linear difference and differential
equations (the
gfunpackage), which have received a very positive review in Computing Reviews and have been incorporated in N. Sloane's superseeker at Bell Labs; tools for systems of multivariate linear
operators (the
Mgfunpackage), including Gröbner bases in Ore algebras, that also treat commutative polynomials and have been the standard way to solve polynomial systems in Maple for a long period
(although the user would not notice it);
Mgfunhas also been chosen at Risc (Linz) as the basis for their package Desing.
We also provide access to our work to scientists who are not using Maple or any other computer algebra system in the form of automatically generated encyclopedias available on the web. The
Encyclopedia of Combinatorial Structures thus contains more than 1000 combinatorial structures for which generating series, enumeration sequences, recurrences and asymptotic behavior have been
computed automatically. It gets more than 16,000 hits per month. The Encyclopedia of Special Functions gathers around 40 special functions for which identities, power series, asymptotic
expansions, graphs,... have been generated automatically, starting from a linear differential equation and its initial conditions. The underlying algorithms and implementations are those of
gfunand
Mgfun. All the production process being automated, the difficult and expensive step of checking each formula individually is suppressed. Available on the web (
[http://algo.inria.fr/esf/]), this encyclopedia also plays the role of a showcase for part of the packages
developed in our project. It gets 27,000 hits per month.
A new package,
MultiSerieshas been developed recently. It implements so-called multi-series, that are series in general asymptotic scales, each of whose coefficient is itself potentially a new series.
This makes it possible to handle in a transparent and dynamic way the problems of finding the proper asymptotic scale for an expansion and of dealing with the indefinite cancellation problem.
This package is designed in such a way that it can take the place of the existing
series,
asymptand
limitMaple functions, in a totally transparent manner.
Tandem repeats are short repetitions that are hotspots for genome recombinations and are also related to some genetic diseases.
TandemSWANsearches for degenerate tandem repeats without insertions and deletions, but with a high substitution rate. It is based on calculation of the repeat statistical significance
and identifies the length of the repeated unit and the number of repetitions. It allows for the identification of weak clustered sites, that are needed for the analysis of several important
regulatory systems such as nitrate/nitrite switch. It is written in C language, using some C++ features.
Software
AhoProallows for counting various probabilities for exceptional words. It relies on automata theory and an updated version of classical Aho-Corasick algorithm. It improves the
computation of existing functions. It takes into account new problems, such as motifs cooccurrences and complex clusters. It is written in C and available on line (
[http://bioinform.genetika.ru/AhoPro/]). It is integrated to SeSiMCMC software of associate
tean GosNIIGenetikam that searches Transcription Factor Binding Sites on Genomes.
New Results
Analysis of algorithms
Nicolas
Broutin
Frédéric
Chyzak
Philippe
Flajolet
Éric
Fusy
Pranav
Kashyap
Frédéric
Meunier
Mireille
Régnier
Bruno
Salvy
The reference book on analytic combinatorics
i) symbolic methods;
(
i
i) complex asymptotics;
(
i
i
i) random structures and probabilities. Point
(
i)addresses the issue of setting up equations that automatically translate a given combinatorial-probabilistic model. Point
(
i
i)aims at developing general-purpose methods for extracting asymptotics on coefficients of generating functions, a task best placed within the framework of complex
analysis. Point
(
i
i
i)is evolving in the direction of classifying the most important processes of combinatorics, in a way that often provides an attractive alternative to stochastic
theory. A global survey of analytic combinatorics appears in
In
An unexpected outcome of the general theory of analytic combinatorics is in the
random generationof large structured combinatorial configurations. Owing to an original confluence of ideas between statistical physics (Boltzmann models), analytic combinatorics
(symbolic approaches), and computer algebra (the systematic evaluation of generating functions near singularities), we can now foresee the existence of a highly general framework in which it
should be possible to express large classes of models of interest in various branches of computer science (from constrained sequences to trees, structured graphs, and automata); then, the
design and the production of extremely efficient simulation algorithms can be automated. The application of these ideas to a large (infinite) family of models, leading to highly efficient
simulation algorithms form sthe subject of
Éric Fusy has published several results giving explicit bijective (i.e., one-to-one) constructions for planar structures such as polygonal meshes and more generally planar maps (graphs
embedded on a planar surface)
Complementary studies in the area of structural combinatorics have been conducted by F. Meunier, during his postdoctoral stay. A paper
Regarding algorithms for massive data sets and data mining, we have designed this year the HyperLogLog counting algorithm, which holds the world record for estimatig
cardinalities(number of distinct elements) of large data ensembles. It is important to note that the very design of the algorithm is based on a subtle exploitation of fine
characteristics of the underlying discrete model. With a few thousand bits of memory, this algorithm makes it possible to estimate the number of distinct elements in a stream of data of several
tens of gigabytes, with an accuracy of few percent (typically 1.5% with 1024 bytes). In this context, no a priori probabilistic assumption is made on the nature of data: the algorithms are
universal. These algorithms have applications in the area of data mining and especially network monitoring. Pranav Kashyap, from IIT Bombay, has developed a comprehensive library and thoroughly
validated a large number of derived algorithms in the area of document comparison and elephant/mice detection. An efficient “sliding window” version of some of these algorithms has also been
finally developed.
Computer Algebra
Alin
Bostan
Frédéric
Chyzak
Philippe
Flajolet
Nicolas
Le Roux
Marc
Mezzarobba
Bruno
Salvy
High precision expansions of power series solutions of differential equations are needed in various branches of computational mathematics, from combinatorics, where the desired power series
is a generating function, to numerical analysis and computational number theory. In
In
The case of linear differential equations with polynomial (rather than power series) coefficients allows for specific algorithms and the Algo project-team has been spending a large part of
its effort on these for many years.
A. Bostan, P. Gaudry (project-team Cacao) and É. Schost study the complexity of computing one or several terms in a linear recurrence with polynomial coefficients in
The analytic solutions of these differential equations can be evaluated efficiently up to very high precisions. In
It is classical that algebraic series are solutions of linear differential equations. In
A follow-up of methods for linear differential equation is an application to linear control systems. A collaboration of F. Chyzak with A. Quadrat (project-team Café) and
D. Robertz (U. Aachen, Germany) has shown that elimination methods for non-commutative polynomials designed in the project permit to make methods developped by A. Quadrat for the
recognition of properties of linear control systems effective. The spectrum of applications includes ODEs, PDEs, multidimensional discrete systems, differential time-delay systems, repetitive
systems, multidimensional convolutional codes, etc. A package, OreModule
[http://
wwwb.
math.
rwth-aachen.
de/
OreModules/
], has been developed
For several years, B. Salvy and A. Bostan have been working jointly with the
Lixlaboratory of the École polytechnique. This work applies recent algorithmic progress on straight-line programs and has produced efficient
algorithms and implementations for geometrical problems. Recently, this work has taken a new direction by extending to the numerical universe methods originally designed to deal with
multiplicities when searching for symbolic solutions of polynomial systems. The results obtained by B. Salvy, G. Lecerf, M. Giusti (École polytechnique) and J.-C. Yakoubsohn
(U. Toulouse) are new versions of Newton's algorithm that are quadratically convergent even in the neighborhood of a multiple root or a cluster of roots for polynomial systems
Structured linear algebra techniques are a versatile set of tools, which enable to deal at once with various types of matrices, with features such as Toeplitz-, Hankel-, Vandermonde- or
Cauchy-likeness. It is classical that such linear systems can be solved, by means of a compact representation, in
 operations, where
operations, where
nis the matrix size and
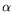 is a measure of the structure. Together with Cl.-P. Jeannerod (project-team Arenaire) and É. Schost, A. Bostan showed that this cost can be reduced to
is a measure of the structure. Together with Cl.-P. Jeannerod (project-team Arenaire) and É. Schost, A. Bostan showed that this cost can be reduced to
 , where
, where
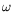 <2.38is a feasible exponent for matrix multiplication. The improvement is
based on re-introducing fast dense linear algebra into operations involving the compact generators of the given matrix. This has consequences for efficient Hermite-Padé approximation and
interpolation of bivariate polynomials.
<2.38is a feasible exponent for matrix multiplication. The improvement is
based on re-introducing fast dense linear algebra into operations involving the compact generators of the given matrix. This has consequences for efficient Hermite-Padé approximation and
interpolation of bivariate polynomials.
Algorithms on sequences
Valentina
Boeva
Philippe
Flajolet
Mireille
Régnier
Bruno
Salvy
Our goal is to combine analytic combinatorics to establish general mathematical results and algorithms that provide efficient optimized implementations for specific data constraints.
Our group studies combinatorial properties of words in order to improve searching algorithms and extract unexpectedly frequent or rare motifs from random sequences. Our main motivation is to
relate such motifs to biological functions on the genome. Ultimately, statistical or probabilistic results are to be integrated into string searching algorithms or software.
Starting from exact counting formulae derived by the tools of analytic combinatorics, we focus on efficient implementations and tight approximation derivations. On the one hand, efficient
implementations have been realized for sets of words, that rely on automata theory. Our main application is the study of words, also called sites on the genome, that may be recognized by
different proteins, in a competing or synergistic manner. On the other hand, approximations have been derived, with a tight error bound. Recent results with A. Denise (Orsay University)
allow to compute the probability of rare events, commonly called
p-valueby bioinformaticians, with a linear algorithm. This is a drastic improvement on the existing exponential algorithm. Tightness of these
p-valueexpressions allows to compute conditional probabilities, and extract weak signals hidden by stronger signals.
P-valuecomputation was implemented in software
SSiMCMCdeveloped at NIIGenetika, with whom we collaborate in associate team
Migec. As a whole, systematic comparisons of commonly used statistical criteria for exceptional words, and precise statements on their validity
domains, have been realized with M. Vandenbogaert. In his master's thesis in 2006, B. Besson studied the mathematical grounds of the so-called Position Specific Scoring Matrix model,
PSSM, in favour among biologists. Notably, he established a link between the number of available experimental data used to build the model, and the precision and significance of the model
obtained. This work was continued in 2007 in a collaboration with J. S. Varré (
Sequoia, Lille). A special attention has been paid to Tandem Repeats. Tandem repeats are short repetitions that are hotspots for genome recombinations
and are also related to some genetic diseases.
TandemSWANIt allows for the identification of weak clustered sites, that are needed for the analysis of several important regulatory systems such as nitrate/nitrite switch. The
originality of the software
TandemSWan, developed jointly in C with NIIGenetika, is the implementation of a procedure to assess the statistical significance of repeats, that can be reused in other softwares such as
Mrepsdeveloped by
Sequoia, Lille, by G. Kucherov. Counting sites clusters, or assessment of a statistical significance for co-occurring motifs had not be addressed
so far. Our algorithm
AhoPro
RNA secondary structures prediction is a hard problem, as a given sequence has an exponential number of potential foldings. It is even worse when pseudo-knots are taken into account. Finding
a structure, e.g., a set of helices, that is common to sequences from phylogenetically closed organisms turned out to be the most efficient way. This comparative approach is meaningful as
sequencing is often realized now for closely related genomes. Our heuristic relies on a few simple probability criteria to chose common helices, and led recently to a variant,
P-DCfold, that deals with pseudo-knots. This work is currently continued by M. Ganjtabesh, PhD student at LIX, that extends our counting results when pseudo-knots are allowed (joint work
with P. Nicodème).
In her thesis cosupervised by M. Régnier, G. Boldina (Almaty University) studies specific motifs that allow for splicing introns. Roughly speaking, the DNA sequence between
splicing sites is a non-coding sequence that does not participate to the translation of DNA into a protein sequence, and therefore should be excised. It turns out that for U2-type introns, that
represent approximately 99,6% of introns for eucaryotes, these motifs are highly degenerated; therefore, they do not resort to usual methods. A definition of a hydropathy profile allows to
capture a biochemical property, and it has been shown that splice sites, and intron types as well, are associated to abnormal profiles
Other Grants and Activities
National Actions
Alea is a national working group dedicated to the analysis of algorithms and random combinatorial structures. It is a meeting place for mathematicians and computer scientists working in the
area of discrete models. It is currently supported by CNRS (GDR A.L.P.) and is globally animated by Philippe Flajolet. In March 2007, the yearly meeting (organized by Frédérique Bassino et
Julien Clément) has gathered in Luminy over 80 participants from about 20 different research laboratories throughout France.
For the period 2003–2007, the Algo project participates in ACI-NIM a national research programme exploring New Interfaces of Mathematics. In this context, we take part in the ACPA project
dedicated to paths and trees, probabilities and algorithms, this jointly with the Universities of Versailles, Bordeaux, and Nancy.
Since 2005 year, a project called FLUX and involving the
Rapproject at
Inriaas well as the University of Montpellier has been funded for a three year period by the national action ACI-MD relative to massive data: our
objective is to develop high performance algorithms for the quantitative analysis of massive data flows an important problem in the monitoring of high speed computer networks.
For the period 2006–2009, the Algo project participates in a programme funded by the National Research Agency (ANR) entitled GECKO for “A Geometric Approach to Complexity and its
Applications". Four teams are involved:
Algo(coordinator) and teams at the École polytechnique, the Universities of Toulouse and Nice. The project concentrates on three classes of objects:
(i) univariate and multivariate polynomials (Newton process, factorization, elimination); (ii) structured matrices (whose coefficients can be polynomials); (iii) linear differential operators
(noncommutative elimination, integration). The aim is to improve significantly the resolution of systems of algebraic or linear differential equations that appear in models, by taking geometry
into account.
The National Research Agency (ANR) has also funded a research project entitled SADA, whose goal is to investigate fundamental properties of random discrete structures and algorithms. The
project duration is 3 years (Dec. 2005–Dec 2008). It involves five teams:
Algo/
Rapfrom
InriaRocquencourt, the Universities of Caen, Versailles, and Bordeaux (coordinator), as well as the Laboratory for Computer Science of the École
polytechnique (LIX).
Bilateral International Relations
Mireille Régnieris the French scientific head of Inria associated team
Migecwith Russian partner GosNIIGenetika. She is also the head of a bioinformatics project supported by the French program ECO-NET, that involves
three teams from Armenia, Kazakhstan and Russia.
She is a participant of IST INTAS: This is a grant to work on comparative genomics of bacteria. This project is joint with TUM (Munchen), CNR-ITB (Milan), NII-Genetika (Moscow) and Moscow
University.
Dissemination
Animation
The
Algoproject runs a biweekly seminar devoted to the analysis of algorithms and related topics. Several partner teams in the grand Paris area attend on
a regular basis, and also take part in a yearly workshop, Alea. Proceedings are collected and edited.
Frédéric Chyzakhas been a co-organizer of the 2007 edition of the French national meeting in computer algebra (JNCF'07), that has gathered some 80 participants in Luminy. He still is
co-organizer of the 2008 edition (JNCF'08). He is a member of the recruiting committee of Univ. Limoges, in mathematics. He has presented the work on algebraic series
Éric Fusyhas been a member of the progam committee of the Workshop on Analytic Algorithms and Combinatorics ANALCO'08.
Philippe Flajoletis an editor of the journal Random Structures and Algorithms, an honorary editor of Theoretical Computer Science, and an honour member of the French association SPECIF.
He also serves as one of the three editors of Cambridge University Press' prestigious series “Encyclopedia of Mathematics and its Applications”.
He serves as Chair of the Steering Committee of the international series of Conferences and Workshops called “Analysis of Algorithms”. The yearly edition attracts some 80 specialists of the
area. He serves in a similar capacity as founder and chair of the French Working Group Alea supported by the GDR-IM [“mathematical informatics”] of CNRS: the yearly meetings are held at Luminy
near Marseilles, and the participation nears 80 every year.
Philippe Flajolet is also an external member of the Recruiting Committee for computer science at the École polytechnique. He is a member of the board of experts for the Canada Research
Chairs.
Mireille Régnierhas coorganized the bioinformatics conference MCCMB'07 in Moscow. She participated to the organization of the new computer science option at the French
agrégationof mathematics. She served in the committee in 2007. She was a member of the recruiting committees of the University of Lille (in computer science). She has been a reviewer for
the PhD C, Herrbach (LRI, Orsay). She was a member of COST-GTRIm for international relationships of Inria.
Bruno Salvyhas been on the program committee of the conference “Analysis of Algorithms”, Nice, 2007 and he is on the program committee for the conference “Formal Power Series and
Algebraic Combinatorics”, Valparaiso, Chile, 2008. He is organizing the working group Computer Algebra of the CNRS GDR IM (“Mathematical Informatics”). He is a member of the editorial board of
the Journal of Symbolic Computation and of the Journal of Algebra (section Computational Algebra).
He is a member of the recruiting committees of the University of Lille (in computer science), of the University of La Rochelle (in mathematics). At Inria Rocquencourt, he has organized the
committees for post-docs and for the recruitment of researchers from other institutes and universities (détachements and délégations) together with Stéphane Gaubert.
This year, he has been a member of the PhD committee of P. Rémy (Mathematics, U. Angers).
Teaching
Alin Bostan,
Frédéric Chyzak, and
Bruno Salvyhave set up and taught a 48h course in computer algebra together with Marc Giusti (from École polytechnique). This course is part of the
Master Parisien de Recherche en Informatique(MPRI).
Frédéric Chyzakteaches a course in computer algebra as a
chargé d'enseignement à temps incompletat École polytechnique.
This year,
Alin Bostanand
Bruno Salvyhave also set up and taught a new 48h course at the
École Normale Supérieureon computer algebra oriented towards experimental mathematics.
Alin Bostan,
Frédéric Chyzak, and
Bruno Salvygave in March 2007 a 4-hour course on “D-finiteness: Algorithms and Applications" at the École Jeunes Chercheurs en Informatique Mathématique (EJCIM'07), in Nancy.
Philippe Flajolethas given a 12 hour course at the Parisian Master of Research in Computer Science (MPRI), on the analysis of algorithms. He has also taught intensive courses on analytic
combinatorics in Santiago de Chile and Barcelona (CRM). In this last course,
Éric Fusyhas been a teaching assistant of Philippe Flajolet; he was co-organising the exercice sessions (5 sessions of 2 hours) with Omer Giménez.
Mireille Régnierteaches a 12/year of courses in the Bioinformatics Master of Évry on combinatorics and algorithms in genomics. She was also invited to give two weeks of postgraduate
courses in Almaty (Kazakhstan).
Participation in conferences, seminars, invitations
Alin Bostan,
Frédéric Chyzak, and
Bruno Salvy's joint work with Grégoire Lecerf and Éric Schost
Frédéric Chyzakhas presented preliminary work joint with A. Bostan and B. Salvy of the project-team and Z. Li (Academy of Mathematics and System Sciences, Beijing) at the
yearly workshop of the Gecko project of the ANR. Expected results are fast algorithms for the computation of least common multiples of linear differential and difference operators.
Philippe Flajolethas been an invited plenary speaker at the joint ACM–SIAM Symposium on Discrete Algorithms (SODA'07, New Orleans) and the “KnuthFest” (Bordeaux, October 2007), and has
given a main tutorial/survey talk at the international conference Analysis of Algorithms (AofA'07, Juan-les-Pins, June 2007). He has been also invited speaker at the British Combinatorics Day
(Oxford, February 2007) Workshop on Probabilistic and Algebraic Methods in Combinatorics (CRM, Barcelona, June 2007). He has given seminars and colloquia at the Universities of Grenoble (number
theory, February 2007), Lyon (Computer Science Colloquium, ENS, April 2007), Orleans (Mathematics Colloquium, September 2007), and Paris-Sud at Orsay (Computer Science Colloquium, December
2007).
Éric Fusyhas given an invited talk at the workshop on combinatorial problems arising from statistical physics at Montreal (Feb. 2007). He has been invited for one week at the university
of Oxford (May 2007) where he colaborated with Bilyana Shoilekova on graph enumeration problems and gave a talk on random generation of planar graphs. He gave one invited talk in Barcelona at
the Conference on Enumeration and Probabilistc Methods in Combinatorics; he also gave two talks in Berlin in July, in the discrete mathematics group at Technische Universitaet Berlin and in the
Algorithmics group at Humboldt Universitaet zu Berlin. He was invited for one week in Zurich in the theoretical computer science group where he colaborated with Konstantinos Panagiotou on
statistical properties of planar graphs and gave an invited talk on planar drawing of triangulations. He was invited by the combinatorics group at Labri, Bordeaux, where he colaborated with
Mireille Bousquet-Mélou and Nicolas Bonichon, and gave a seminar on bijective constructions for planar maps. He gave an invited talk at the AMS Special Session on Algorithmic Probability and
Combinatorics, held at DePaul University Chicago (Oct. 2007).
Nicolas Le Rouxgave a talk about the computation of formal local series solutions of linear partial differential equations systems at the meeting of the Gecko project of the ANR held in
INRIA Sophia Antipolis (november 2007).
Frédéric Meuniergave a talk at the SMAI 2007 conference on a combinatorial optimization problem – the so-called paint shop problem. At the AofA'07 conference in Juan-les-Pins, he
presented his joint work
Mireille Régniervisited three times the associated team NIIGenetika in Moscow. She gave a talk at
Inria-NIH workshop in Washington, DC and at workshop AlgoBio in Moscow. She was invited by scientific council of Nantes University for a presentation
on Genomics.
Bruno Salvyhas been invited to give a talk at the Joint Mathematics Meeting of the American Mathematical Society and the Mathematical Association of America, on
Gfun: 20 years laterin New Orleans. He presented
Foreign Visitors
A large number of our visitors have given talks at the seminar of the project. This year, we received: Bilyana Shoilekova, Oxford University, U.K.; Michel Schellekens, National University of
Ireland, Cork, Ireland Alfredo Viola, University of Montevideo, Uruguay; Ziming Li, Academy of Mathematics and System Sciences, Beijing, China; Manuel Kauers, Johanes Kepler University, Linz
Austria; Vsevolod Makeev, Laboratory of Bioinformatics, GosNIIgenetika, Moscow, Russia; Julia Medvedeva, Russian Academy of Sciences, Moscow, Russia; Ivan V. Kulakovsky, Russian Academy of
Sciences, Moscow, Russia; Zara Kirakossian, Yerevan State University, Yerevan, Republic of Armenia; Mikhail Roytberg, Institute of Mathematical Problems in Biology, Puschino, Russia.
![]() operations, where
operations, where
![]() is a measure of the structure. Together with Cl.-P. Jeannerod (project-team Arenaire) and É. Schost, A. Bostan showed that this cost can be reduced to
is a measure of the structure. Together with Cl.-P. Jeannerod (project-team Arenaire) and É. Schost, A. Bostan showed that this cost can be reduced to
![]() , where
, where
![]() <2.38is a feasible exponent for matrix multiplication. The improvement is
based on re-introducing fast dense linear algebra into operations involving the compact generators of the given matrix. This has consequences for efficient Hermite-Padé approximation and
interpolation of bivariate polynomials.
<2.38is a feasible exponent for matrix multiplication. The improvement is
based on re-introducing fast dense linear algebra into operations involving the compact generators of the given matrix. This has consequences for efficient Hermite-Padé approximation and
interpolation of bivariate polynomials.