Overall Objectives
Introduction
computer arithmetic
integer computation
approximate computation
floating-point representation
elementary function
reliability of numerical software
multiple-precision arithmetic
interval arithmetic
computer algebra
finite field
linear algebra
lattice basis reduction
VLSI circuit
FPGA circuit
low-power operator
embedded chips
The Arénaire project aims at elaborating and consolidating knowledge in the field of Computer Arithmetic. Reliability, accuracy, and performance are the major goals that drive our studies.
Our goals address various domains such as floating-point numbers, intervals, rational numbers, or finite fields. We study basic arithmetic operators such as adders, dividers, etc. We work on
new operators for the evaluation of elementary and special functions (
log,
cos,
erf, etc.), and also consider the composition of previous operators. In addition to these studies on the arithmetic operators themselves, our research
focuses on specific application domains (cryptography, signal processing, linear algebra, lattice basis reduction, etc.) for a better understanding of the impact of the arithmetic choices on
solving methods in scientific computing.
We contribute to the improvement of the available arithmetic on computers, processors, dedicated or embedded chips, etc., both at the hardware level and at the software level. Improving
computing does not necessarily mean getting more accurate results or getting them faster: we also take into account other constraints such as power consumption, code size, or the reliability of
numerical software. All branches of the project focus on algorithmic research and on the development and the diffusion of corresponding libraries, either in hardware or in software. Some
distinctive features of our libraries are numerical quality, reliability, and performance.
The study of the number systems and, more generally, of data representations is a first topic of uttermost importance in the project. Typical examples are: the redundant number systems used
inside multipliers and dividers; alternatives to floating-point representation for special purpose systems; finite field representations with a strong impact on cryptographic hardware circuits;
the performance of an interval arithmetic that heavily depends on the underlying real arithmetic.
Another general objective of the project is to improve the validation of computed data, we mean to provide more guarantees on the quality of the results. For a few years we have been
handling those validation aspects in the following three complementary ways: through better qualitative properties and specifications (correct rounding, error bound representation, and
portability in floating-point arithmetic); by proposing a development methodology focused on the proven quality of the code; by studying and allowing the cooperation of various kinds of
arithmetics such as constant precision, intervals, arbitrary precision and exact numbers.
These goals may be organized in four directions:
hardware arithmetic,
software arithmetic for algebraic and elementary functions,
validation and automation, and
arithmetics and algorithms for scientific computing. These directions are not independent and have strong interactions. For example, elementary functions are also studied for hardware
targets, and scientific computing aspects concern most of the components of Arénaire.
Hardware Arithmetic.From the mobile phone to the supercomputer, every computing system relies on a small set of computing primitives implemented in hardware. Our goal is to study the
design of such arithmetic primitives, from basic operations such as the addition and the multiplication to more complex ones such as the division, the square root, cryptographic primitives,
and even elementary functions. Arithmetic operators are relatively small hardware blocks at the scale of an integrated circuit, and are best described in a structural manner: a large
operator is assembled from smaller ones, down to the granularity of the bit. This study requires knowledge of the hardware targets (ASICs, FPGAs), their metrics (area, delay, power), their
constraints, and their specific language and tools. The input and output number systems are typically given (integer, fixed-point of floating-point), but internally, non-standard internal
number systems may be successfully used.
Algebraic and Elementary Functions.Computer designers still have to implement the basic arithmetic functions for a medium-size precision. Addition and multiplication have been much
studied but their performance may remain critical (silicon area or speed). Division and square root are less critical, however there is still room for improvement (e.g. for division, when
one of the inputs is constant). Research on new algorithms and architectures for elementary functions is also very active. Arénaire has a strong reputation in these domains and will keep
contributing to their expansion. Thanks to past and recent efforts, the semantics of floating-point arithmetic has much improved. The adoption of the IEEE-754 standard for floating-point
arithmetic has represented a key point for improving numerical reliability. Standardization is also related to properties of floating-point arithmetic (invariants that operators or
sequences of operators may satisfy). Our goal is to establish and handle new properties in our developments (correct rounding, error bounds, etc.) and then to have those results integrated
into the future computer arithmetic standards.
Validation and Automation.Validation corresponds to some guarantee on the quality of the evaluation. Several directions are considered, for instance the full error (approximation
plus rounding errors) between the exact mathematical value and the computed floating-point result, or some guarantee on the range of a function. Validation also comprises a proof of this
guarantee that can be checked by a proof checker. Automation is crucial since most development steps require specific expertise in floating-point computing that can neither be required from
code developers nor be mobilised manually for every problems.
Arithmetics and Algorithms.When conventional floating-point arithmetic does not suffice, we use other kinds of arithmetics. Especially in the matter of error bounds, we work on
interval arithmetic libraries, including arbitrary precision intervals. Here a main domain of application is global optimization. Original algorithms dedicated to this type of arithmetic
must be designed in order to get accurate solutions, or sometimes simply to avoid divergence (e.g., infinite intervals). We also investigate exact arithmetics for computing in algebraic
domains such as finite fields, unlimited precision integers, and polynomials. A main objective is a better understanding of the influence of the output specification (approximate within a
fixed interval, correctly rounded, exact, etc.) on the complexity estimates for the problems (e.g., linear algebra in mathematical computing).
Our work in Arénaire since its creation in 1998, and especially since 2002, provides us a strong expertise in computer arithmetic. This knowledge, together with the technology progress both
in software and hardware, draws the evolution of our objectives towards the
synthesis of validated algorithms.
Highlights of the Year
2007 has seen a decisive convergence of the revision of the IEEE-754 standard for floating-point arithmetic, a process begun in 2000. In its current draft, which many consider close to
final, the standard advocates correct rounding of elementary functions, which will lead to more accurate results and better reproducibility. This is a result of many years of concerted efforts,
covering most of the directions listed above, by members of Arénaire.
Scientific Foundations
Introduction
As stated above, four major directions in Arénaire are
hardware arithmetic,
algebraic and elementary functions,
validation and automation, and
arithmetics and algorithms. For each of those interrelated topics, we describe below the tools and methodologies on which it relies.
Hardware Arithmetic
A given computing application may be implemented using different technologies, with a large range of trade-offs between the various aspects of performance, unit cost, and non-recurring costs
(including development effort).
A software implementation, targeting off-the-shelf microprocessors, is easy to develop and reproduce, but will not always provide the best performance.
For cost or performance reasons, some applications will be implemented as application specific integrated circuits (ASICs). An ASIC provides the best possible performance
and may have a very low unit cost, at the expense of a very high development cost.
An intermediate approach is the use of reconfigurable circuits, or field-programmable gate arrays (FPGAs).
In each case, the computation is broken down into elementary operations, executed by elementary hardware elements, or
arithmetic operators. In the software approach, the operators used are those provided by the microprocessor. In the ASIC or FPGA approaches, these operators have to be built by the
designer, or taken from libraries. Our goals include studying operators for inclusion in microprocessors and developing hardware libraries for ASICs or FPGAs.
Operators under study.Research is active on algorithms for the following operations:
Basic operations (addition, subtraction, multiplication), and their variations (multiplication and accumulation, multiplication or division by constants, etc.);
Algebraic functions (division, inverse, and square root, and in general, powering to an integer, and polynomials);
Elementary functions (sine, cosine, exponential, etc.);
Combinations of the previous operations (norm, for instance).
A hardware implementation may lead to better performance than a software implementation for two main reasons: parallelism and specialization. The second factor, from the arithmetic point of
view, means that specific data types and specific operators, which would require costly emulation on a processor, may be used. For example, some cryptography applications are based on modular
arithmetic and bit permutations, for which efficient specific operators can be designed. Other examples include standard representations with non-standard sizes, and specific operations such as
multiplication by constants.
Hardware-oriented algorithms.Many algorithms are available for the implementation of elementary operators (see for instance
The choice of the number systems used for the intermediate results is crucial. For example, a redundant system, in which a number may have several encodings, will allow for more design
freedom and more parallelism, hence faster designs. However, the hardware cost can be higher. As another example, the power consumption of a circuit depends, among other parameters, on its
activity, which in turn depends on the distribution of the values of the inputs, hence again on the number system.
Alternatives exist at many levels in this algorithm exploration. For instance, an intermediate result may be either computed, or recovered from a precomputed table.
Parameter exploration.Once an algorithm is chosen, optimizing its implementation for area, delay, accuracy, or energy consumption is the next challenge. The best solution depends on the
requirements of the application and on the target technology. Parameters which may vary include the radix of the number representations, the granularity of the iterations (between many simple
iterations, or fewer coarser ones), the internal accuracies used, the size of the tables (see
The parameter space quickly becomes huge, and the expertise of the designer has to be automated. Indeed, we do not design operators, but
operator generators, programs that take a specification and some constraints as input, and output a synthesizable description of an operator.
Algebraic and Elementary Functions
Elementary Functions and Correct Rounding.Many libraries for elementary functions are currently available. We refer to
Though the IEEE-754 standard does not deal with these functions, there is some attempt to reproduce some of their mathematical properties, in particular symmetries. For instance,
monotonicity can be obtained for some functions in some intervals as a direct consequence of accurate internal computations or numerical properties of the chosen algorithm to evaluate the
function; otherwise it may be
verydifficult to guarantee, and the general solution is to provide it through correct rounding. Preserving the range (e.g.,
atan(
x)
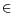 [-
[-
 /2,
/2,
 /2]) may also be a goal though it may conflict with correct rounding (when
supported).
/2]) may also be a goal though it may conflict with correct rounding (when
supported).
Concerning the correct rounding of the result, it is not required by the IEEE-754 standard: during the elaboration of this standard, it was considered that correctly rounded elementary
functions was impossible to obtain at a reasonable cost, because of the so called
Table Maker's Dilemma: an elementary function is evaluated to some internal accuracy (usually higher than the target precision), and then rounded to the target precision. What is the
minimum accuracy necessary to ensure that rounding this evaluation is equivalent to rounding the exact result, for all possible inputs? This question cannot be answered in a simple manner,
meaning that correctly rounding elementary functions requires arbitrary precision, which is very slow and resource-consuming.
Indeed, correctly rounded libraries already exist, such as MPFR (
[http://
www.
mpfr.
org]), the Accurate Portable Library released by IBM in 2002, or the
libmcrlibrary, released by Sun Microsystems in late 2004. However they have worst-case execution time and memory consumption up to 10,000 worse than usual libraries, which is the main
obstacle to their generalized use.
We have focused in the previous years on computing bounds on the intermediate precision required for correctly rounding some elementary functions in IEEE-754 double precision. This allows us
to design algorithms using a tight precision. That makes it possible to offer the correct rounding with an acceptable overhead: we have experimental code where the cost of correct rounding is
negligible in average, and less than a factor 10 in the worst case.
It also enables to prove the correct-rounding property, and to show bounds on the worst-case performance of our functions. Such worst-case bounds may be needed in safety critical
applications as well as a strict proof of the correct rounding property. Concurrent libraries by IBM and Sun can neither offer a complete proof for correct rounding nor bound the timing because
of the lack of worst-case accuracy information. Our work actually shows a posteriori that their overestimates for the needed accuracy before rounding are however sufficient. IBM and Sun for
themselves could not provide this information. See also §
Approximation and Evaluation.The design of a library with correct rounding also requires the study of algorithms in large (but not arbitrary) precision, as well as the study of more
general methods for the three stages of the evaluation of elementary functions: argument reduction, approximation, and reconstruction of the result.
When evaluating an elementary function for instance, the first step consists in reducing this evaluation to the one of a possibly different function on a small real interval. Then, this last
function is replaced by an approximant, which can be a polynomial or a rational fraction. Being able to perform those processes in a very cheap way while keeping the best possible accuracy is a
key issue
Adequation Algorithm/Architecture.Some special-purpose processors, like DSP cores, may not have floating-point units, mainly for cost reasons. For such integer or fixed-point processors,
it is thus desirable to have software support for floating-point functions, starting with the basic operations. To facilitate the development or porting of numerical applications on such
processors, the emulation in software of floating-point arithmetic should be compliant with the IEEE-754 standard; it should also be very fast. To achieve this twofold goal, a solution is to
exploit as much as possible the characteristics of the target processor (instruction set, parallelism, etc.) when designing algorithms for floating-point operations.
So far, we have successfully applied this “algorithm/architecture adequation” approach to some VLIW processor cores from STMicroelectronics, in particular the ST231; the ST231 cores have
integer units only, but for their applications (namely, multimedia applications), being able to perform basic floating-point arithmetic very efficiently was necessary. When various
architectures are targeted, this approach should further be (at least partly) automated. The problem now is not only to write some fast and accurate code for one given architecture, but to have
this optimized code generated automatically according to various constraints (hardware resources, speed and accuracy requirements).
Validation and Automation
Validating a code, or generating a validated code, means being able to prove that the specifications are met. To increase the level of reliability, the proof should be checkable by a formal
proof checker.
Specifications of qualitative aspects of floating-point codes.A first issue is to get a better formalism and specifications for floating-point computations, especially concerning the
following qualitative aspects:
specification:typically, this will mean a proven error bound between the value computed by the program and a mathematical value specified by the user in some high-level format;
tight error bound computation;
floating-point issues:regarding the use of floating-point arithmetic, a frequent concern is the portability of code, and thus the reproducibility of computations; problems can be due
to successive roundings (with different intermediate precisions) or the occurrence of underflows or overflows;
precision:the choice of the method (compensated algorithm versus double-double versus quadruple precision for instance) that will yield the required accuracy at given or limited cost
must be studied;
input domains and output ranges:the determination of input domain or output range also constitutes a specification/guarantee of a computation;
other arithmetics, dedicated techniques and algorithms for increased precision:for studying the quality of the results, most of conception phases will require
multiple-precisionor
exactsolutions to various algebraic problems.
Certification of numerical codes using formal proof.Certifying a numerical code is error-prone. The use of a proof assistant will ensure the code correctly follows its specification.
This certification work, however, is usually a long and tedious work, even for experts. Moreover, it is not adapted to an incremental development, as a small change to the algorithm may
invalidate the whole formal proof. A promising approach is the use of automatic tools to generate the formal proofs of numerical codes with little help from the user.
Instead of writing code in some programming language and trying to prove it, we can design our own language, well-suited to proofs (e.g., close to a mathematical point of view, and allowing
metadata related to the underlying arithmetics such as error bounds, ranges, and so on), and write tools to generate code. Targets can be a programming language without extensions, a
programming language with some given library (e.g., MPFR if one needs a well-specified multiple-precision arithmetic), or a language internal to some compiler: the proof may be useful to give
the compiler some knowledge, thus helping it to do particular optimizations. Of course, the same proof can hold for several targets.
We worked in particular also on the way of giving a formal proof for our correctly rounded elementary function library. We have always been concerned by a precise proof of our
implementations that covers also details of the numerical techniques used. Such proof concern is mostly absent in IBM's and Sun's libraries. In fact, many misroundings were found in their
implementations. They seem to be mainly due to coding mistakes that could have been avoided with a formal proof in mind. In CRlibm we have replaced more and more hand-written paper proofs by
Gappa verified proof scripts that are partially generated automatically by other scripts. Human error is better prevented.
Integrated and interoperable automatic tools.Various automatic components have been independently introduced above, see §
Arithmetics and Algorithms
When computing a solution to a numerical problem, an obvious question is that of the
qualityof the produced numbers. One may also require a certain level of quality, such as: approximate with a given error bound, correctly rounded, or –if possible– exact. The question
thus becomes twofold: how to produce such a well-specified output and at what cost? To answer it, we focus on
polynomial and integer matrix operations,
Euclidean latticesand
global optimization, and study the following directions:
We investigate new ways of producing well-specified results by resorting to various arithmetics (intervals, Taylor models, multi-precision floating-point, exact). A first
approach is to
combinesome of them: for example, guaranteed enclosures can be obtained by mixing Taylor model arithmetic with floating-point arithmetic
We also study the impact of certification on algorithmic complexity. A first approach there is to augment existing algorithms with validated error bounds (and not only
error estimates). This leads us to study the (im)possibility of
computing such boundson the fly at a negligible cost. A second approach is to study the
algorithmic changesneeded to achieve a higher level of quality without, if possible, sacrificing for speed. In exact linear algebra, for example, the fast algorithms recently
obtained in the bit complexity model are far from those obtained decades ago in the algebraic complexity model.
Numerical Algorithms using Arbitrary Precision Interval Arithmetic.When validated results are needed, interval arithmetic can be used. New problems can be solved with this arithmetic,
which provides sets instead of numbers. In particular, we target the global optimization of continuous functions. A solution to obviate the frequent overestimation of results is to increase the
precision of computations.
Our work is twofold. On the one hand, efficient software for arbitrary precision interval arithmetic is developed, along with a library of algorithms based on this arithmetic. On the other
hand, new algorithms that really benefit from this arithmetic are designed, tested, and compared.
To reduce the overestimation of results, variants of interval arithmetic have been developed, such as Taylor models arithmetic or affine arithmetic. These arithmetics can also benefit from
arbitrary precision computations.
Algorithms for Exact Linear Algebra and Lattice Basis Reduction.The techniques for exactly solving linear algebra problems have been evolving rapidly in the last few years, substantially
reducing the complexity of several algorithms (see for instance
We recently started a direction around lattice basis reduction. Euclidean lattices provide powerful tools in various algorithmic domains. In particular, we investigate applications in
computer arithmetic, cryptology, algorithmic number theory and communications theory. We work on improving the complexity estimates of lattice basis reduction algorithms and providing better
implementations of them, and on obtaining more reduced bases. The above recent progress in linear algebra may provide new insights.
Certified Computing.Most of the algorithmic complexity questions that we investigate concern algebraic or bit-complexity models for exact computations. Much less seems to be known in
approximate computing, especially for the complexity of computing (certified) error bounds, and for establishing bridges between exact, interval, and constant precision complexity estimates. We
are developing this direction both for a theoretical impact, and for the design and implementation of algorithm synthesis tools for arithmetic operators, and mathematical expression
evaluation.
Software
Introduction
Arénaire proposes various software and hardware realizations that are accessible from the web page
[http://
www.
ens-lyon.
fr/
LIP/
Arenaire/
Ware/
]. We describe below only those which progressed in 2007.
CRlibm: a Library of Elementary Functions with Correct Rounding
F.
de Dinechin
C.
Lauter
J.-M.
Muller
G.
Revy
elementary function
libm
double precision arithmetic
correct rounding
The CRlibm project aims at developing a mathematical library (
libm) which provides implementations of the double precision C99 standard elementary functions,
correctly rounded in the four IEEE-754 rounding modes,
with a comprehensive proof of both the algorithms used and their implementation,
sufficiently efficient in average time, worst-case time, and memory consumption to replace existing
libms transparently.
In 2007, we released the versions 0.17beta1, 0.18beta1 and 1.0beta1 with 7 more functions:
sin(

x),
cos(

x)
tan(

x)and their inverse functions, and the power function
xy. We also have published our algorithm for correctly-rounded logarithms
The library includes a documentation which makes an extensive tutorial on elementary function software development.
The library has been downloaded more than 3500 times. Its focus on performance and correctness has enabled acceptance of correct rounding as a goal of the revised floating-point standard
IEEE-754R. It is also considered for inclusion in the GNU compiler collection.
Status:
Beta release /
Target:
ia32, ia64, Sparc, PPC /
License:
LGPL /
OS:
Unix /
Programming Language:
C /
URL:
[http://
www.
ens-lyon.
fr/
LIP/
Arenaire]
Sollya: a toolbox of numerical algorithms for the development of safe numerical codes
C.
Lauter
S.
Chevillard
N.
Jourdan
numerical algorithms
infinite norm
plot
Remez algorithm
automatic implementation of a function
proof generation
Sollya aims at providing a safe, user-friendly, all-in-one environment for manipulating numerical functions. Sollya provides both safe and efficient algorithms: certified infinite norm,
multiple-precision faithful-rounding evaluator of composed functions, efficient numerical approximate algorithms for searching approximations of the zeros of a function, finding a polynomial
approximation, etc.
Sollya comes with an interpreter for the Sollya scripting language. Existing Sollya primitives can be extended with dynamically-linked user code.
Sollya used to be a small software project called
arenaireplot. In 2007, it has been highly improved (quicker implementation of existing algorithms and implementation of new features such as the programming language).
Sollya has been used for implementing the polynomial evaluation inside the CRlibm functions added in 2007, along with their Gappa proofs.
Status:
Release scheduled for December 2007 /
Target:
ia32, ia64, PPC, ia32-64, other /
License:
CeCILL-C /
OS:
Unix /
Programming Language:
C /
URL:
[http://
sollya.
gforge.
inria.
fr/
]
FPLibrary: a Library of Operators for “Real” Arithmetic on FPGAs
J.
Detrey
F.
de Dinechin
arithmetic operators
function evaluation
floating-point
LNS
FPGA
FPLibrary is a
VHDLlibrary that describes arithmetic operators (addition, subtraction, multiplication, division, and square root) for two formats of representation
of real numbers: floating-point, and logarithmic number system (LNS). These formats are parametrized in precision and range. FPLibrary is the first hardware library to offer parametrized
hardware architectures for elementary functions in addition to the basic operations. In 2007, an efficient floating-point accumulator has been added.
FPLibrary is being used by tens of academic or industrial organizations in the world. In 2007, its trigonometric operators have been included in a standard set of benchmarks defined by the
Altera corporation and the university of Berkeley.
Status:
Stable /
Target:
FPGA /
License:
GPL/LGPL /
OS:
Unix, Linux, Windows /
Programming Language:
VHDL /
URL:
[http://
www.
ens-lyon.
fr/
LIP/
Arenaire/
Ware/
FPLibrary/
]
FloPoCo: a Floating-Point Core generator for FPGAs
F.
de Dinechin
arithmetic operators
function evaluation
floating-point
fixed-point
FPGA
The purpose of the FloPoCo project is to explore the many ways in which the flexibility of the FPGA target can be exploited in the arithmetic realm. FloPoCo is a generator of operators
written in C++ and outputting synthesizable VHDL. The first release of FloPoCo, in 2007, include multipliers of an integer or a floating-point number by a constant, and a generalization of the
long accumulator introduced by Kulisch.
Status:
Beta release /
Target:
FPGA /
License:
GPL/LGPL /
OS:
Unix, Linux, Windows /
Programming Language:
C++ /
URL:
[http://
www.
ens-lyon.
fr/
LIP/
Arenaire/
Ware/
FloPoCo/
]
MPFI: Multiple Precision Floating-Point Interval Arithmetic
N.
Revol
S.
Chevillard
C.
Lauter
H.D.
Nguyen
interval arithmetic
arbitrary precision
Library in C for interval arithmetic using arbitrary precision (arithmetic and algebraic operations, elementary functions, operations on sets). Modifications made this year mainly concern
the correction of bugs.
Status:
Beta release /
Target:
any /
License:
LGPL /
OS:
Unix, Linux, Windows (Cygwin) /
Programming Language:
C /
URL:
[http://
mpfi.
gforge.
inria.
fr/
]
MEPLib: Machine-Efficient Polynomials Library
N.
Brisebarre
J.-M.
Muller
S.
Torres
polynomial approximation
minimax approximation
floating-point arithmetic
fixed-point arithmetic
polytopes
linear programming
This software library is developed within a national initiative Ministry Grant ACI “New interfaces of mathematics” (see §
MEPLib is a library for automatic generation of polynomial approximations of functions under various constraints, imposed by the user, on the coefficients of the polynomials. The constraints
may be on the size in bits of the coefficients or the values of these coefficients or the form of these coefficients. It relies on the linear programming tool PIP and interacts with the Sollya
library. It should be useful to engineers or scientists for software and hardware implementations.
Status:
Beta release /
Target:
various processors, DSP, ASIC, FPGA /
License:
GPL /
OS:
Unix, Linux, Windows (Cygwin) /
Programming Language:
C /
URL:
[http://
lipforge.
ens-lyon.
fr/
projects/
meplib]
Gappa: a Tool for Certifying Numerical Programs
G.
Melquiond
roundoff error
formal proof
certification
floating-point arithmetic
fixed-point arithmetic
Given a logical property involving interval enclosures of mathematical expressions, Gappa tries to verify this property and generates a formal proof of its validity. This formal proof can be
machine-checked by an independent tool like the Coq proof-checker, so as to reach a high level of confidence in the certification.
Since these mathematical expressions can contain rounding operators in addition to usual arithmetic operators, Gappa is especially well suited to prove properties that arise when certifying
a numerical application, be it floating-point or fixed-point. Gappa makes it easy to compute ranges of variables and bounds on absolute or relative roundoff errors.
Gappa is being used in several projects, including CRlibm, FLIP, Sollya, and CGal
In 2007, the syntax of user rules was extended in order to formally prove a wider set of properties. The accessibility of Gappa was improved when starting new proofs. The support library was
extended with new results on floating-point arithmetic and relative errors.
Status:
Beta release /
Target:
any /
License:
GPL, CeCILL /
OS:
any /
Programming Language:
C++ /
URL:
[http://
lipforge.
ens-lyon.
fr/
www/
gappa/
]
FLIP: a floating-point library for integer processors
C.-P.
Jeannerod
N.
Jourdan
G.
Revy
single-precision arithmetic
correct rounding
integer processor
VLIW
FLIP is a C library for efficient software support of single precision floating-point arithmetic on processors without floating-point hardware units, such as VLIW or DSP processors for
embedded applications. The current target architecture is the VLIW ST200 family from STMicroelectronics (especially the ST231 cores).
In 2007 we have completely rewritten the code for add, sub, square, multiply, and for the most basic algebraic functions: square root, inverse square root, reciprocal, division. This
resulted in substantial speed-ups compared to the previous codes. The tools used for the design include Gappa (§
Status:
Beta release /
Target:
VLIW processors (ST200 family from STMicroelectronics) /
License:
LGPL /
OS:
Linux, Windows /
Programming Language:
C /
URL:
[http://
lipforge.
ens-lyon.
fr/
www/
flip/
]
MPFR
V.
Lefèvre
arbitrary precision
correct rounding
MPFR is a multiple-precision floating-point library with correct rounding developed by the Arénaire and Cacao projects. The computation is both efficient and has a well-defined semantics. It
copies the good ideas from the IEEE-754 standard. MPFR 2.3.0 was released on 29 August 2007.
The main changes done in 2007 are: new functions, improved tests (they allowed to find bugs in very particular cases), better documentation, bug fixes (which mainly consisted in completing
the implementation of some functions on particular cases).
Several software systems use MPFR, for example: the KDE calculator Abakus by Michael Pyne; the ALGLIB.NET project; CGAL (Computational Geometry Algorithms Library) developed by the
Geometrica team (INRIA Sophia-Antipolis); the Fluctuat tool developed and used internally at the CEA; Gappa (§
Status:
stable /
Target:
any /
License:
LGPL /
OS:
Unix, Windows (Cygwin or MinGW) /
Programming Language:
C /
URL:
[http://
www.
mpfr.
org/
]
fpLLL
D.
Stehlé
I.
Morel
G.
Villard
lattice reduction
floating-point arithmetic
Given a set of vectors with integer coordinates, the aim of fpLLL is to compute an LLL-reduced basis of the euclidean lattice that is spanned by the vectors. The reduction is performed
efficiently thanks to the use of floating-point arithmetic for the computation of the underlying Gram-Schmidt orthogonalization (central in LLL).
The computation is both fully rigorous and efficient. A hierarchy of heuristic/fast and provable/slower variants is used in order to provide these two properties simultaneously.
fpLLL is used in the SAGE project, and an earlier version of fpLLL is in MAGMA (
[http://
magma.
maths.
usyd.
edu.
au/
magma/
]). fpLLL has been used for computations in fields as diverse as cryptography, computer arithmetic, algorithmic number theory and algorithmic group theory.
In 2007, fpLLL underwent a massive update, in major part by David Cadé, an ENS Master student who was hosted in the team during the summer. The new version, fpLLL-2.1, is faster, and more
importantly considerably easier to use and extend.
Status:
Version 2.1.6 /
Target:
any /
License:
GPL /
OS:
Linux /
Programming Language:
C++ /
URL:
[http://
perso.
ens-lyon.
fr/
damien.
stehle/
english.
html]
Exhaustive Tests of the Mathematical Functions
V.
Lefèvre
elementary function
correct rounding
The programs to search for the worst cases for the correct rounding of mathematical functions (
exp,
log,
sin,
cos, etc.) using Lefèvre's algorithm have been further improved, in particular:
More robust control scripts, working in more environments, with more automation.
More supported functions.
One of the scripts has entirely been reimplemented, using MPFR instead of Maple, and with more features.
The scripts have been modified to be able to support special functions whose worst-case information has been used for
Profiling information can now be automatically generated (with very little overhead) and used. This allows to gain up to 22% on Opteron processors.
New Results
Hardware Arithmetic Operators
N.
Brisebarre
J.
Detrey
F.
de Dinechin
R.
Michard
J.-M.
Muller
N.
Veyrat-Charvillon
ASIC
FPGA
circuit generator
fixed-point
floating-point
LNS
arithmetic operators
function evaluation
integrated circuit
digit-recurrence algorithms
division
square-root
exponential
logarithm
trigonometric
sine
cosine
tridiagonal systems
Digit-recurrence Algorithms
Milos D. Ercegovac (University of California at Los Angeles) and J.-M. Muller have improved their results of 2004 on digit recurrence algorithms for complex square-root (for
which they obtained a best paper award at the ASAP-2004 conference). They have published the obtained results in a special issue of the Journal of VLSI Signal Processing
The E-method, introduced by Ercegovac, allows efficient parallel solution of diagonally dominant systems of linear equations in the real domain using simple and highly regular hardware.
Since the evaluation of polynomials and certain rational functions can be achieved by solving the corresponding linear systems, the E-method is an attractive general approach for function
evaluation. Milos D. Ercegovac and J.-M. Muller have generalized the E-method to complex linear systems, and have shown some potential applications such as the evaluation of complex
polynomials by a digit-recurrence method
mfor
m-digit precision. The basic modules are similar to left-to-right multipliers. The interconnections between the modules are digit-wide
Multiplication in Finite Fields
With J.-L. Beuchat, T. Miyoshi and E. Okamoto (Tsukuba University, Japan), J.-M. Muller has written a survey
GF(
p)and
GF(
pn). They present a generic architecture based on five processing elements and introduce a classification of several algorithms based on their model. They provide the readers with
a detailed description of each scheme which should allow them to write a VHDL description or a VHDL code generator.
Improvements on a Method to Compute Hardware Function Evaluation Operators
R. Michard and N. Veyrat-Charvillon have worked with A. Tisserrand, former team member now at LIRMM. They have improved a new method to optimize hardware operators for the
evaluation of fixed-point unary functions. Starting from an ideal minimax polynomial approximation of the function, it first looks for a polynomial whose coefficients are fixed-point numbers
of small size. It then bounds accurately the evaluation error using the Gappa tool. This work was first published at the Sympa conference in 2006 and the improvements are to be published in
2008
Power Comparison of Evaluation Methods on FPGAs
R. Michard has started a work on power consumption. It is a study of several hardware operator families and aims at evaluating the consumption of each to be able to choose what kind
of operator is required when designing a circuit. This work is based on Xilinx Power Estimator to characterize operators on Xilinx FPGAs. This work is in progress and will be the subject of a
publication in 2008.
Hardware Floating-point Elementary Functions
Three hardware algorithms for elementary functions implemented in FPLibrary were published in 2007: a dual sine/cosine operator up to single precision, along with a study of the tradeoffs
involved, by J. Detrey, F. de Dinechin
Applications
With O. Creţ, I. Trestian, L. Creţ, L. Vǎcariu and R. Tudoran from the Technical University of Cluj-Napoca, F. de Dinechin has worked on the implementation of a
hardware accelerator used for the simulation of coils to be used for transcranial magnetic stimulation
When FPGAs are Better at Floating-point than Processors
This collaboration with users of Arénaire's floating-point operators has pointed out that the flexibility of FPGA hardware is currently underused when floating-point applications are
ported to this target. With his collaborators from UCTN, F. de Dinechin has written a prospective survey of the many ways to better exploit this flexibility
Hardware Implementation of the
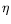
TPairing in Characteristic 3
Since their introduction in constructive cryptographic applications, pairings over (hyper)elliptic curves are at the heart of an ever increasing number of protocols. Software
implementations being rather slow, the study of hardware architectures became an active research area.
In collaboration with J.-L. Beuchat and E. Okamoto (Tsukuba Univ., Japan) and M. Shirase and T. Takagi (Future Univ. of Hakodate, Japan), N. Brisebarre and J. Detrey
proposed in
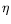
Tpairing in characteristic three. These algorithms involve addition, multiplication, cubing, inversion, and sometimes cube root extraction over
 . The authors also propose a hardware accelerator based on a unified arithmetic operator able to perform the operations required by a given algorithm. and describe the implementation
of a compact coprocessor for the field
. The authors also propose a hardware accelerator based on a unified arithmetic operator able to perform the operations required by a given algorithm. and describe the implementation
of a compact coprocessor for the field
 given by
given by
![Im3 ${\#120125 _3{[x]}/{(x^97+x^12+2)}}$](math_image_3.png) , which compares favorably with other solutions described in the open literature. The article
, which compares favorably with other solutions described in the open literature. The article
Efficient Polynomial Approximation
N.
Brisebarre
S.
Chevillard
J.-M.
Muller
S.
Torres
floating-point arithmetic
polynomial approximation
minimax
lattice basis reduction
closest vector problem
We keep on developing methods for generating the best, or at least very good, polynomial approximations (with respect to the infinite norm or the
L2norm) to functions, among polynomials whose coefficients follow size constraints (e.g., the degree-
icoefficient has at most
mifractional bits, or it has a given, fixed, value). This is a key step in the process of function evaluation.
A method
About the
L2norm, N. Brisebarre and G. Hanrot (LORIA, INRIA Lorraine) published a complete study of the problem
We are developing libraries for generating such polynomial approximations (see Sections
Efficient Floating-Point Arithmetic and Applications
N.
Brisebarre
C.-P.
Jeannerod
C.
Lauter
V.
Lefèvre
J.-M.
Muller
G.
Revy
floating-point arithmetic
multiplication
Newton-Raphson iteration
rounding of algebraic functions
square root
emulation
integer processor
Multiplication by Constants
N. Brisebarre and J.-M. Muller
Chand
 be the constants
be the constants

These two constant are exactly representable in double precision arithmetic. If executed with a fused multiply-add with round-to-nearest mode, the following algorithm

will always return the floating-point number
u2that is nearest

x.
Computation of Integer Powers in Floating-point Arithmetic
P. Kornerup (Odense University, Denmark), V. Lefèvre and J.-M. Muller
Emulation of Floating-point Square Roots on VLIW Integer Processors
Correctly-rounded floating-point square roots can be obtained in many ways: by iterative methods (restoring, non-restoring, SRT), by multiplicative methods (Newton, Goldschmidt), or by
methods based on the evaluation of high-quality polynomial approximants. With H. Knochel and C. Monat (STMicroelectronics, Grenoble), C.-P. Jeannerod and G. Revy
Correct Rounding of Elementary Functions
N.
Brisebarre
S.
Chevillard
F.
de Dinechin
C.
Lauter
V.
Lefèvre
J.-M.
Muller
D.
Stehlé
elementary functions
libm
correct rounding
double precision
interval arithmetic
machine-assisted proofs
power function
Worst-Cases of Periodic Functions for Large Arguments
G. Hanrot, V. Lefèvre, D. Stehlé and P. Zimmermann
O(2
0.676
p)for a precision of
pbits. The efficiency of the algorithm was shown on the largest IEEE-754 double precision binade for the sine function, and some corresponding bad cases were given.
Bounds for Correct Rounding of the Algebraic Functions
N. Brisebarre and J.-M. Muller have published a method that makes it possible to get bounds on the accuracy with which intermediate calculations must be carried-on to allow for
correctly-rounded algebraic functions
Exact Cases of the Power Function
C. Lauter and V. Lefèvre
xy) function in double precision. The correct rounding of the power function is currently based on Ziv's iterative approximation process. In order to ensure its termination, cases when
xyfalls on a rounding boundary (a floating-point number or a midpoint between two consecutive floating-point numbers) must be filtered out.
This new rounding boundary test consists of a few comparisons with pre-computed constants. These constants are deduced from worst cases for the Table Maker's Dilemma, searched over a small
subset of the input domain. This is a novel use of such worst-case bounds.
Machine-assisted Proofs
F. de Dinechin, C. Q. Lauter and G. Melquiond have worked on the use of the Gappa tool for proving an elementary function
Implementation of a Certified Infinite Norm
S. Chevillard and C. Lauter have worked on the problem of providing a certified bound on the infinite norm of a function
Interval Arithmetic, Taylor Models and Multiple or Arbitrary Precision
F.
Cháves
N.
Revol
interval arithmetic
Taylor models
formal proof
PVS
implementation
arbitrary precision
Formal Proofs on Taylor Models Arithmetic
Our implementation of Taylor models arithmetic is developed in PVS. We provide new strategies to recursively apply operators on Taylor models, with as few intervention of the user as
possible
Accurate Implementations of Taylor Models with Floating-point Arithmetic
The implementation of Taylor models arithmetic may use floating-point arithmetic to benefit from the speed of the floating-point implementation. In
Automatic Adaptation of the Computing Precision
When a given computation does not yield the required accuracy, the computation can be done (either restarted or continued) using an increasing computing precision. A natural question is
how to increase the computing precision in order to minimize the time overhead, compared to the case where the optimal computing precision is known in advance and used for the computation. We
generalize a result by Kreinovich and Rump: we study the case where the computation can benefit from results obtained with a lower precision and thus is not restarted but rather continued. We
also propose an asymptotically optimal strategy for adapting the computing precision, which has an overhead tending to 1 when the optimal (unknown) precision tends to infinity.
Linear Algebra and Lattice Basis Reduction
C.-P.
Jeannerod
I.
Morel
H. D.
Nguyen
N.
Revol
G.
Villard
D.
Stehlé
real matrix
integer matrix
polynomial matrix
structured matrix
approximant basis
lattice
certified computation
verification algorithm
matrix error bound
algebraic complexity
reduction to matrix multiplication
LLL lattice reduction
strong lattice reduction
asymptotically fast algorithm
Verification Algorithms
Most of the algorithmic complexity questions we have been investigating in the past were in algebraic or bit-complexity models. Our typical target problems were system solution, matrix
inversion or canonical forms (see
Rfactor of the matrix
QRfactorization. Currently, the corresponding algorithm costs only six times as much as for computing the factorization itself numerically. The approach is applied for certifying the LLL
reducedness of output bases of floating point and heuristic LLL variants.
H.D. Nguyen starts his PhD under the supervision of N. Revol and G. Villard. He studies and experiments the choice of the computing precision and the use of interval arithmetic
to get certified enclosures of the error on the solution of linear systems, computed using floating-point arithmetic.
Algebraic Complexity for Linear Algebra: Structured and Black Box Matrices
Linear systems with structure such as Toeplitz, Vandermonde or Cauchy-likeness arise in many algebraic problems, like Hermite-Padé approximation or interpolation of bivariate polynomials.
The cost of solving such systems was known to be in
 , where
, where
nis the size of the matrix and
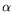 is its displacement rank. With A. Bostan (INRIA, project-team Algo) and É. Schost (University of Western Ontario), C.-P. Jeannerod showed in
is its displacement rank. With A. Bostan (INRIA, project-team Algo) and É. Schost (University of Western Ontario), C.-P. Jeannerod showed in
 , where
, where
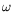 is a feasible exponent for matrix multiplication. (In both cases, such costs are obtained by means of Las Vegas probabilistic algorithms.) Since
is a feasible exponent for matrix multiplication. (In both cases, such costs are obtained by means of Las Vegas probabilistic algorithms.) Since
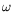 <2.38, this yields costs of order
<2.38, this yields costs of order
 and thus asymptotically faster solutions to the algebraic problems mentioned above. On the other hand, this bridges a gap between dense linear algebra (where
and thus asymptotically faster solutions to the algebraic problems mentioned above. On the other hand, this bridges a gap between dense linear algebra (where
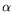 =
=
nand for which system solving has cost
 and structured linear algebra (where
and structured linear algebra (where
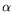 =
=
O(1)and for which system solving has cost
 ).
).
Block projections have recently been used, in
 operations). Unfortunately, the correctness of this algorithm depends on the existence of block projections of matrices and this has been conjectured but not proved. In
operations). Unfortunately, the correctness of this algorithm depends on the existence of block projections of matrices and this has been conjectured but not proved. In
 operations; a basis for the null space of a sparse matrix — and a certification of its rank — are obtained at the same cost. An application to Kaltofen and Villard's
Baby-Steps/Giant-Steps algorithms for the determinant and Smith Form of an integer matrix yields algorithms requiring
operations; a basis for the null space of a sparse matrix — and a certification of its rank — are obtained at the same cost. An application to Kaltofen and Villard's
Baby-Steps/Giant-Steps algorithms for the determinant and Smith Form of an integer matrix yields algorithms requiring
 machine operations. The algorithms are probabilistic of the Las Vegas type.
machine operations. The algorithms are probabilistic of the Las Vegas type.
Probabilistic Reduction of Rectangular Lattices
Lattice reduction algorithms such as LLL and its floating-point variants have a very wide range of applications in computational mathematics and in computer science: polynomial
factorisation, cryptology, integer linear programming,
etc. It can occur that a lattice to be reduced has a dimension which is small with respect to the dimension of the space in which it lies. This happens within the LLL algorithm itself.
A. Akhavi and D. Stehlé
Improving LLL Reduction Algorithms
I. Morel starts his PhD under the supervision of D. Stehlé and G. Villard, he is studying LLL reduction algorithms.
D. Stehlé and G. Villard propose a componentwise perturbation analysis of the
QRfactorization for LLL reduced matrices
A Tighter Analysis of Kannan's Algorithm
The security of lattice-based cryptosystems such as NTRU, GGH and Ajtai-Dwork essentially relies upon the intractability of computing a shortest non-zero lattice vector and a closest
lattice vector to a given target vector in high dimensions. The best algorithms for these tasks are due to Kannan, and, though remarkably simple, their complexity estimates had not been
improved since over twenty years. Kannan's algorithm for solving the shortest vector problem (SVP) is in particular crucial in Schnorr's celebrated block reduction algorithm, on which rely
the best known generic attacks against the lattice-based encryption schemes mentioned above. G. Hanrot and D. Stehlé
Lower Bounds for Strong Lattice Reduction
The Hermite-Korkine-Zolotarev reduction plays a central role in strong lattice reduction algorithms. By building upon a technique introduced by Ajtai, G. Hanrot and
D. Stehlé
 bit operations in dimension
bit operations in dimension
d. This matches the best complexity upper bound known for this algorithm
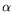
dand
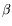
dthat are essentially equal to the best upper bounds. They also showed the existence of particularly bad bases for Schnorr's hierarchy of reductions.
Code and Proof Synthesis
S.
Chevillard
C.-P.
Jeannerod
N.
Jourdan
C.
Lauter
V.
Lefèvre
N.
Revol
G.
Revy
S.
Torres
G.
Villard
certified active code generation
automation
code for the evaluation of mathematical expressions
representation of mathematical expressions with extra knowledge
Our goal is to produce a certified active code generator. Starting from specifications given by the user, such a generator produces a target code (that may be modified, at a low level, by
this user) along with a proof that the final code corresponds to the given specifications. The specifications we consider are, roughly speaking, mathematical expressions; the generated code
evaluates these expressions using floating-point arithmetic and it satisfies prescribed quality criteria: for instance, it returns the correctly rounded result.
More precisely, we aim at doing accurate mathematics using a programming language, typically C. Our tools are the operators and functions specified by the IEEE-754 standard for
floating-point arithmetic, the compilation of mathematical expressions and optimizations related to the context (ranges of the variables...). We simultaneously aim at providing certificates and
proofs concerning the transformations performed during the code generation, using tools such as Gappa (cf. §
The advantages of this approach are mainly the gain in productivity: a minor modification of the input would otherwise be time-consuming and error-prone if handled manually. A second main
advantage is the gain in abstraction, through better understanding of models, specifications and constraints.
During this year, we worked on deciding upon the architecture of such a project (cf. §
![]() [-
[-
![]() /2,
/2,
![]() /2]) may also be a goal though it may conflict with correct rounding (when
supported).
/2]) may also be a goal though it may conflict with correct rounding (when
supported).