Scientific Foundations
Introduction
We survey the different fields, which underline the scientific basis of CARTE, enhancing the aspects around adverse computations.
Continuous Computation Theory
Today's classical computability and complexity theory deals with discrete time and space models of computation. However, discrete time models of machines working on a continuous space have
been considered: see e.g.
Blum Shub and Smalemachines
Continuous models of computation lead to particular continuous dynamical systems. More generally, continuous time dynamical systems arise as soon as one attempts to model systems that evolve
over a continuous space with a continuous time. They can even emerge as natural descriptions of discrete time or space systems. Utilizing continuous time systems is a common approach in fields
such as biology, physics or chemistry, when a huge population of agents (molecules, individuals, ...) is abstracted into real quantities such as proportions or thermodynamic data.
Computation theory of continuous dynamical systems allow us to understand both the hardness of questions related to continuous dynamical systems and the computational power of continuous
analog models of computations.
A survey on continuous-time computation theory, with discussions of relations between both approaches, co-authored by Olivier Bournez and Manuel Campagnolo, can be found in
Rewriting
Rewriting has reached some maturity and the rewriting paradigm is now widely used for specifying, modelizing, programming and proving. It allows for easily expressing deduction systems in a
declarative way, for expressing complex relations on infinite sets of states in a finite way, provided they are countable. Programming languages and environments have been developed, which have
a rewriting based semantics. Let us cite
ASF+SDF
For basic rewriting, many techniques have been developed to prove properties of rewrite systems like confluence, completeness, consistency or various notions of termination. In a weaker
proportion, proof methods have also been proposed for extensions of rewriting like equational extensions, consisting of rewriting modulo a set of axioms, conditional extensions where rules are
applied under certain conditions only, typed extensions, where rules are applied only if there is a type correspondence between the rule and the term to be rewritten, and constrained
extensions, where rules are enriched by formulas to be satisfied
An interesting aspect of the rewriting paradigm is that it allows automatable or semi-automatable correctness proofs for systems or programs. Indeed, properties of rewriting systems as those
cited above are translatable to the deduction systems or programs they formalize and the proof techniques may directly apply to them.
Another interesting aspect is that it allows characteristics or properties of the modelized systems to be expressed as equational theorems, often automatically provable using the rewriting
mechanism itself or induction techniques based on completion
Algorithmic Game Theory
Game theory aims at discussing situations of competition between rational players
For general games, the key concept of Nash equilibrium was proposed in the early 50s by John Nash in
Algorithmic game theory differs from game theory by taking into account algorithmic and complexity aspects. Indeed, historically main developpments of classical game theory have been
realized in a mathematical context, without true considerations on effectivness of constructions.
Game theory and algorithmic game theory have large domains of applications in theoretical computer science: it has been used to understand complexity of computing equilibria
Computer Virology
From an historical point of view, the first official virus appeared in 1983 on Vax-PDP 11. In the very same time, a series of papers was published which always remain a reference in computer
virology: Thompson
The literature which explains and discusses about practical issues is quite extensive, see for example Ludwig's book
A virus is essentially a self-replicating program inside an adversary environment. Self-replication has a solid background based on works on fixed point in
 -calculus and on studies of Von Neumann
-calculus and on studies of Von Neumann
A virus infect programs by modifying them
A virus copies itself and can mutate
Virus spreads throughout a system
The above scientific foundation justifies our position to use the word virus as a generic word for self-replicating malwares. (There are yet a difference. A malware has a payload, and virus
may not have one.) For example, worms are an autonous self-replicating malwares and so fall into our definition. In fact, the current malware taxonomy (virus, worms, trojans, ...) is unclear
and subject to debate.
Application Domains
Computations by Dynamical Systems
Analog Models of Computations
Computability
Complexity
Continuous time computation theories
Continuous time systems arise as soon as one attempts to model systems that evolve over a continuous space with a continuous time. They can even emerge as natural descriptions of discrete
time or space systems. Utilizing continuous time systems is a common approach in fields such as biology, physics or chemistry, when a huge population of agents (molecules, individuals, ...)
is abstracted into real quantities such as proportions or thermodynamic data
Understanding computation theories for continuous systems leads to understand hardness of verification and control of these systems. This has been used to discuss problems in fields as
diverse as verification (see e.g.
Some systems carrying out computations are intrinsically continuous. This is the case, for example, of some more or less futuristic models such as quantum models of computations, or models
based on space-time curves, but also of some mechanical
Understanding computation theories for continuous systems leads, in this context, to characterize the computational power of these machines. This has been used to discuss, for example, the
power of models such as the General Purpose Analog Computer of Shannon
Since continuous time systems are conducive to modeling huge populations, one might speculate that they will have a prominent role in analyzing massively parallel systems such as the
Internet. This is one deep motivation of our work on computation theories for continuous systems.
Analysis and verification of adversary systems
The other research direction on dynamical systems we are interested in is the study of properties of adversary systems or programs, i.e. of systems whose behavior is unknown or indistinct,
or which do not have classical expected properties. We would like to offer proof and verification tools, to guarantee the correctness of such systems.
One one hand, we are interested in continuous and hybrid systems. In a mathematical sense, a hybrid system can be seen as a dynamical system, whose transition function does not satisfy the
classical regularity hypotheses, like continuity, or continuity of its derivative. The properties to be verified are often expressed as reachability properties. For example, a safety property
is often equivalent to (non-)reachability of a subset of unsure states from an initial configuration, or to stability (with its numerous variants like asymptotic stability, local stability,
mortality, etc ...). Thus we will essentially focus on verification of these properties in various classes of dynamical systems.
We are also interested by rewriting techniques, used to describe dynamic systems, in particular in the adversary context. As they were initially developed in the context of automated
deduction, the rewriting proof techniques, although now numerous, are not yet adapted to the complex framework of modelization and programming. An important stake in the domain is then to
enrich them to provide realistic validation tools, both in providing finer rewriting formalisms and their associated proof techniques, and in developing new validation concepts in the
adversary case, i.e. when usual properties of the systems like, for example, termination are not verified.
For more than five years, we have been developing specific procedures for property proofs of rewriting, for the sake of programming, in particular with inductive techniques, already
applied with success to termination under strategies
The last two results take place in the context of adversary computations, since they allow for proving that even a divergent program, in the sense where it does not terminate, can give the
expected results.
We especially intend to continue to study the termination property, and its impact on other properties, since it seems to be central in several research directions of the project:
Until now it was very used for deciding properties like confluence, completeness or consistency. Its weakening or its absence, very frequent in real cases, throws us
into the adversary context.
It is a tool for the analysis of resources.
Thoroughly analyzing divergence by non-termination can be an approach for modeling the continuous.
A crucial element of safety and security of software systems is the problem of resources. We are working in the field of Implicit Computational Complexity. Interpretation based methods
like Quasi-interpretations (QI) or sup-interpretations, are the approach we have been developing these last five years, see
Robust and Distributed Algorithms, Algorithmic Game Theory
Distributed Systems
Models for Dynamics
Algorithmic Game Theory
One of the problems related to distributed algorithmics corresponds to the minimization of resources (time of transit, quality of services) in problems of transiting information (routing
problems, group telecommunications) in telecommunication networks.
Each type of network gives rise to natural constraints on models. For example, a network is generally modeled by a graph. The material and physical constraints on each component of the
network (routers, communication media, topology, etc ...) result in different models. One natural objective is then to build algorithms to solve those types of problems on various models.
One can also constraint solutions to offer certain guarantees: for example the property of self-stabilization, which expresses that the system must end in a correct state whatever its initial
state is; or certain guarantees of robustness: even in the presence of a small proportion of Byzantine actors, the final result will remain correct; even in the presence of rational actors with
divergent interests, the final result will remain acceptable.
Algorithms of traditional distributed algorithmics were designed with the strong assumption that the interest of each actor does not differ from the interest of the group. For example, in a
routing problem, classical distributed algorithms do not take into account the economic interests of the various autonomous systems, and only try to minimize criteria such as shortest
distances, completely ignoring the economical consequences of decisions for involved agents.
If one wants to have more realistic models, and take into account the way the different agents behave, one gets more complex models.
However, today, one gets models which are hard to analyse. For example,
Models of dynamism are missing: e.g., how to model a negotiation in a distributed auction mechanism for the access to a telecommunications service,
only few methods are known to guarantee that the equilibrium reached by such systems remains in some domains that could be qualified as safe or reasonable,
there is almost no method discussing the speed of convergence, when there is convergence,
only a little is known about the time and space resources necessary to establish some techniques to guarantee correct behavior.
Thus, it is important to reconsider the algorithms of the theory of distributed algorithmics, under the angle of the competitive interests that involved agents can have (Adversary
computation). This requires to include/understand well how to reason on these types of models.
Computer Virology
Virus
worms
self-replication
recursion theory
defense
attack
propagation
formal grammars
Nowadays, our thoughts lead us to define four different research tracks, that we are describing below.
The theoretical track.
It is rightful to wonder why there is only a few fundamental studies on computer viruses while it is one of the important flaws in software engineering. The lack of theoretical studies
explains maybe the weakness in the anticipation of computer diseases and the difficulty to improve defenses. For these reasons, we do think that it is worth exploring fundamental aspects, and
in particular self-reproducing behaviors.
The virus detection track.
The crucial question is how to detect viruses or self-replicating malwares. Cohen demonstrated that this question is undecidable. The anti-virus heuristics are based on two methods. The
first one consists in searching for virus signatures. A signature is a regular expression, which identifies a family of viruses. There are obvious defect. For example, an unknown virus will
not be detected, like ones related to a 0-day exploit. We strongly suggest to have a look at the independent audit
The virus protection track.
The aim is to define security policies in order to prevent malaware propagation. For this, we need to (i) to define what is a computer in different programming languages and setting, (ii)
to take into consideration resources like time and space. We think that formal methods like rewriting, type theory, logic, or formal languages, should help to define the notion of a
formal immune system, which defines a certified protection.
The experimentation track.
This study on computer virology leads us to propose and construct a “high security lab” in which experiments can be done in respect with the French law. This project of “high security lab”
in one of the main project of the CPER 2007-2013.
New Results
Analog Computations
Olivier
Bournez
Daniel
Graça
Emmanuel
Hainry
Analog Computations
Computability
Complexity
There are many ways to model analog computers. Unifying those models is therefore a crucial matter as opposed to the discrete case, as there is no property stating that those models are
equivalent. It is possible to distinguish two groups in these models: on one side, continuous time models; on the other side, discrete-time models working on continuous structures as a model
derived from Turing machines. The first group contains in particular some sets of functions defined by Moore in
There are few comparisons between classes of functions from the first group and from the second group, and in particular, there were almost no result of equality.
It is known that Euler's Gamma function is computable according to computable analysis, while it cannot be generated by Shannon's General Purpose Analog Computer (GPAC). This example has
often been used in order to argue that the GPAC is less powerful than digital computations.
However, as we demonstrated in
In
In
Analysis and verification of adversary systems
Isabelle
Gnaedig
Rewriting
Induction
Narrowing
Abstraction
Strategy
Termination
Completeness
In previous works, we had proposed a method for specifically proving, by explicit induction, termination of rewriting under strategies. The proof principle consists, for a given term
rewriting system, in establishing on the ground term algebra that every term terminates i.e. has only finite derivations, assuming that any smaller term terminates. For that, we develop proof
trees representing the possible derivations from any term using the term rewriting system. Two mechanisms are used, namely abstraction, introducing variables that represent ground terms in
normal form and schematize normalization of subterms, and narrowing, schematizing rewriting in different ways according to the possible ground instances of the terms studied. These two
mechanisms deal with constraints used to ensure the inductive process, and to control the growth of the proof trees.
From three distinct procedures, initially given for respectively proving termination of rewriting with the innermost, the outermost and the local strategies, factorizing the common
mechanisms, we have obtained a generic algorithm, combining three proof steps, that exactly correspond to the basic principles of the induction mechanism: an abstraction, a narrowing and a stop
step. We have then studied the ordering constraints generated by our inductive proof principle, in order to automate the proof algorithm for the different strategies. This year, we have
completed our results, giving a completeness theorem for our procedure, and discussing the limits of abstraction and narrowing to handle strategies, which finishes an article to appear in
Inspired by the applicability of our inductive approach for other properties than termination
Pof a reduction relation on a
 -algebra. Generalizing the notion of normal form when
-algebra. Generalizing the notion of normal form when
Pis termination, and of constructor form when
Pis completeness, we have defined the notion of
P-canonical form. Our abstraction mechanism then consists in replacing subterms by
P-canonical forms. We have formalized the notion of simulation of a reduction relation
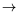 by another one, in general a narrowing relation, to prove
by another one, in general a narrowing relation, to prove
P. The induction mechanism then works on two distinct sets: a basis set containing the irreducible elements for
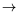 , and a set of patterns for which proof trees are developed, simulating rewriting trees. We finally showed how this mechanism is instantiated to express the proof procedures already
given for termination under strategies, and weak properties like weak termination or completeness
, and a set of patterns for which proof trees are developed, simulating rewriting trees. We finally showed how this mechanism is instantiated to express the proof procedures already
given for termination under strategies, and weak properties like weak termination or completeness
The probabilistic framework, recently proposed in
Implicit Computational Complexity
Jean-Yves
Marion
Guillaume
Bonfante
Romain
Péchoux
complexity
resource upper bound
ramification
tiering
light linear logic
quasi-interpretation
sup-interpretation
The goal of implicit computational complexity is to give ontogenetic model of computational complexity. We follow two lines of research. The first is related to the initial ramified
recursion theory due to Leivant and Marion. The second is related to interpretation methods, quasi-interpretation and sup-interpretation, in order to provide an upper bound on some
computational resources, which are necessary for a program execution. This approach seems to have some practical interests, and we develop a software Crocus that automatically infer complexity
upper bounds of functional programs.
In
O(
nk)(for each k, where
nis the input size, over a RAM type of machine). Next, by a diagonalization argument, we obtain a function, which jumps outside polynomial time. The whole system is presented as a
lambda-calculus with dependent type.
We pursue our investigation on quasi-interpretations and sup-interpretations. In
On a more theoretical side, Guillaume Bonfante and Yves Guiraud began the study of polygraphs from their intensional properties. Compared to the usual rewriting framework, polygraphs
intrinsically allows functions with more than one output. They showed in a first step that polygraphs are well suited to divide and conquer programs
Models of dynamics in Networks
Olivier
Bournez
Johanne
Cohen
Octave
Boussaton
algorithmic game theory
dynamics
graphs
networks
telecommunications
We considered a model of interdomain routing proposed by a partner from SOGEA project. We proved that the model has no pure Nash equilibria, even for 4 nodes. Proof of convergence of the
fictious player dynamics for the corresponding network has been established for some specific cases.
We reviewed the different models of dynamism in literature in game theory, in particular models from evolutionary game theory. We presented some ways to use them to realize distributed
computations in
Octave Boussaton is currently working on the theory of learning equilibria, in particular in Wardrop routing networks. The proof of the convergence of a specific learning strategy has been
established for some networks. The result has been presented in
erover, we presented both a game theoretic and a distributed algorithmic approach for the transit price negotiation problem in the interdomain routing framework. We analyzed the behavior of
providers on a specific scenario, mainly by considering the simple but not simplistic case of one source and one destination. The analysis of the centralized transit price negotiation problem
shows that the only one non cooperative equilibrium is when the lowest cost provider takes all the market. The perspective of the game being repeated makes cooperation possible while
maintaining higher prices. Then, we considered the system under a distributed framework. Indeed, in reality the nodes only have a local view of the game including the topology and thus the
nature and the length of the possible routes. We simulated the behavior of the distributed system under a simple price adjustment strategy and analyzed whether it matches the theoretical
results or not. This work is published in
Computer virology
Guillaume
Bonfante
Matthieu
Kaczmarek
Jean-Yves
Marion
Malware
detection
self-reproduction
learning
art of war
We work on computer virology since 2005. Our research has led us to develop three subjects on computer virology.
The first subject is about the fundamental aspect of computer virology. As we have said previously, computer virology leans on self-reproduction system theory and in particular on Kleene's
recursion Theorem. In particular, we obtained a classification of viruses based on the strenghnens of the recursion theorem which is necessary to use in order to construct a virus. Following
our previous study, Guillaume Bonfante, Matthieu Kaczmarek and Jean-Yves Marion in
The second subject concerns the defense by new malware detection methods. We have presented in
The goal of the last subject is to understand the impact of computer virology in the society and to explain it. Anne Bonfante and Jean-Yves Marion, in
Finally, it is worth to mention that Guillaume Bonfante and Jean-Yves Marion was guest editors of the Journal of Computer Virology, Springer. See
And because there is no special drawer to put this result, Jérôme Besombes and Jean-Yves Marion have published in
![]() -calculus and on studies of Von Neumann
. More precisely we establish in
that Kleene's second recursion theorem
is the cornerstone from which viruses and infection scenarios can be defined and classified. The bottom line of a
virus is behavior is
-calculus and on studies of Von Neumann
. More precisely we establish in
that Kleene's second recursion theorem
is the cornerstone from which viruses and infection scenarios can be defined and classified. The bottom line of a
virus is behavior is