Scientific Foundations
Analysis and control of fluids and of fluid-structure interactions
Navier-Stokes equations
Korteweg de Vries equations
analysis and control of fluids and fluid-structure interactions
motion of solids in viscous fluids
The problems we consider are modeled by the Navier-Stokes, Euler or Korteweg de Vries equations (for the fluid) coupled to the equations governing the motion of the solids. One of the main
difficulties of this problem comes from the fact that the domain occupied by the fluid is one of the unknowns of the problem. We have thus to tackle a
free boundary problem.
The control of fluid flows is a major challenge in many applications: aeronautics, pollution issues, regulation of irrigation channels or of the flow in pipelines, etc. All these problems
cannot be easily reduced to finite dimensional models so a methodology of analysis and control based on
pde's is an essential issue. In a first approximation the motion of fluid and of the solids can be decoupled. The most used models for an
incompressible fluid are given by the Navier-Stokes or by the Euler equations.
The optimal open loop control approach of these models has been developed from both the theoretical and numerical points of view. Controllability issues for the equations modeling the fluid
motion are by now well understood (see, for instance, Imanuvilov
In real applications the fluid is often surrounded by or it surrounds an elastic structure. In the above situation one has to study fluid-structure interactions. This subject has been
intensively studied during the last years, in particular for its applications in noise reduction problems, in lubrication issues or in aeronautics. In this kind of problems, a
pde's system modeling the fluid in a cavity (Laplace equation, wave equation, Stokes, Navier-Stokes or Euler systems) is coupled to the equations
modeling the motion of a part of the boundary. The difficulties of this problem are due to several reasons such as the strong nonlinear coupling and the existence of a free boundary. This
partially explains the fact that applied mathematicians have only recently tackled these problems from either the numerical or theoretical point of view. One of the main results obtained in our
project concerns the global existence of weak solutions in the case of a two-dimensional Navier–Stokes fluid (see
In
N-dimensional model for the interactive motion of a rigid body (a ball) immersed in a viscous fluid. After proving the existence and uniqueness of a strong global in time solution, we
compute the first term in the asymptotic development of solutions. We prove that the asymptotic profile of the fluid is the heat kernel with an appropriate total mass. The
 estimates we get allow us to describe the asymptotic trajectory of the center of mass of the rigid body as well.
estimates we get allow us to describe the asymptotic trajectory of the center of mass of the rigid body as well.
The numerical methods used for computing the solutions of fluid or fluid structure problems in a direct setting (i.e., with given inputs) considerably progressed during the last years. In
our project, we have proposed in
Another topic of great interest is the control of the interface of two fluids (typically water and air) by using as input the velocity of a moving wall which is a part of the boundary. One
of the most popular models for this problem is given by the shallow water equations (Saint Venant equations) which neglect the dispersive effects. The controllability of several important
systems governed by this type of equations has received a considerable attention during the last decade. Let us mention here the important work by Coron
Frequency domain methods for the analysis and control of systems governed by
pde's
Helmholtz equation
time-reversal
control and stabilization
numerical approximation of LQR problems
We use frequency tools to analyze different types of problems. The first one concerns the control, the optimal control and the stabilization of systems governed by
pde's, and their numerical approximations. The second one concerns time-reversal phenomena, while the last one deals with numerical approximation of
high-frequency scattering problems.
Control and stabilization for skew-adjoint systems
The first area concerns theoretical and numerical aspects in the control of a class of PDE's. More precisely, in a semigroup setting, the systems we consider have a skew-adjoint generator.
Classical examples are the wave, the Bernoulli-Euler or the Schrödinger equations. Our approach is based on an original characterization of exact controllability of second order conservative
systems proposed by K. Liu
In the case of finite dimensional systems one of the main applications of frequency domain methods consists in designing robust controllers, in particular of
 type. Obtaining the similar tools for systems governed by PDE's is one of the major challenges in the theory of infinite dimensional systems. The first difficulty which has to be
tackled is that, even for very simple PDE systems, no method giving the parametrisation of all stabilizing controllers is available. One of the possible remedies consists in considering known
families of stabilizing feedback laws depending on several parameters and in optimizing the
type. Obtaining the similar tools for systems governed by PDE's is one of the major challenges in the theory of infinite dimensional systems. The first difficulty which has to be
tackled is that, even for very simple PDE systems, no method giving the parametrisation of all stabilizing controllers is available. One of the possible remedies consists in considering known
families of stabilizing feedback laws depending on several parameters and in optimizing the
 norm of an appropriate transfer function with respect to this parameters. Such families of feedback laws yielding computationally tractable optimization problems are now available for
systems governed by PDE's in one space dimension.
norm of an appropriate transfer function with respect to this parameters. Such families of feedback laws yielding computationally tractable optimization problems are now available for
systems governed by PDE's in one space dimension.
Time-reversal
The second area in which we make use of frequency tools is the analysis of time-reversal for harmonic acoustic waves. This phenomenon described in Fink
Time-reversal has many applications covering a wide range of fields, among which we can cite
medicine(kidney stones destruction or medical imaging),
sub-marine communicationand
non destructive testing. Let us emphasize that in the case of time-harmonic acoustic waves, time-reversal is equivalent to phase conjugation and involves the Helmholtz operator.
In
Numerical approximation of high-frequency scattering problems
This subject deals mainly with the numerical solution of the Helmholtz or Maxwell equations for open region scattering problems. This kind of situation can be met e.g. in radar systems in
electromagnetism or in acoustics for the detection of underwater objects like submarines.
Two particular difficulties are considered in this situation
the wavelength of the incident signal is small compared to the characteristic size of the scatterer,
the problem is set in an unbounded domain.
These two problematics limit the application range of most common numerical techniques. The aim of this part is to develop new numerical simulation techniques based on microlocal analysis
for modeling the propagation of rays. The importance of microlocal techniques in this situation is that it makes possible a local analysis both in the spatial and frequency domain. Therefore,
it can be seen as a kind of asymptotic theory of rays which can be combined with numerical approximation techniques like boundary element methods. The resulting method is called the
On-Surface Radiation Condition method.
Observability, controllability and stabilization in the time domain
linear evolution equations
stabilization
coupling mechanism
boundary control
Controllability and observability have been set at the center of control theory by the work of R. Kalman in the 1960's and soon they have been generalized to the infinite-dimensional
context. The main early contributors have been D.L. Russell, H. Fattorini, T. Seidman, R. Triggiani, W. Littman and J.-L. Lions. The latter gave the field an enormous impact with his book
Even in the finite-dimensional case, despite the fact that the linear theory is well established, many challenging questions are still open, concerning in particular nonlinear control
systems.
In some cases it is appropriate to regard external perturbations as unknown inputs; for these systems the synthesis of observers is a challenging issue, since one cannot take into account
the term containing the unknown input into the equations of the observer. While the theory of observability for linear systems with unknown inputs is well established, this is far from being
the case in the nonlinear case. A related active field of research is the uniform stabilization of systems with time-varying parameters. The goal in this case is to stabilize a control system
with a control strategy independent of some signals appearing in the dynamics, i.e., to stabilize simultaneously a family of time-dependent control systems and to characterize families of
control systems that can be simultaneously stabilized.
One of the basic questions in finite- and infinite-dimensional control theory is that of motion planning, i.e., the explicit design of a control law capable of driving a system from an
initial state to a prescribed final one. Several techniques, whose suitability depends strongly on the application which is considered, have been and are being developed to tackle such a
problem, as for instance the continuation method, flatness, tracking or optimal control. Preliminary to any question regarding motion planning or optimal control is the issue of
controllability, which is not, in the general nonlinear case, solved by the verification of a simple algebraic criterion. A further motivation to study nonlinear controllability criteria is
given by the fact that techniques developed in the domain of (finite-dimensional) geometric control theory have been recently applied successfully to study the controllability of
infinite-dimensional control systems, namely the Navier–Stokes equations (see Agrachev and Sarychev
Implementation
Dicretization
Riccati equation
This is a transverse research axis since all the research directions presented above have to be validated by giving control algorithms which are aimed to be implemented in real control
systems. We stress below some of the main points which are common (from the implementation point of view) to the application of the different methods described in the previous sections.
For many infinite dimensional systems the use of co-located actuators and sensors and of simple proportional feed-back laws gives satisfying results. However, for a large class of systems of
interest it is not clear that these feedbacks are efficient, or the use of co-located actuators and sensors is not possible. This is why a more general approach for the design of the feedbacks
has to be considered. Among the techniques in finite dimensional systems theory those based on the solutions of infinite dimensional Riccati equation seem the most appropriate for a
generalization to infinite dimensional systems. The classical approach is to approximate an LQR problem for a given infinite dimensional system by finite dimensional LQR problems. As it has
been already pointed out in the literature this approach should be carefully analyzed since, even for some very simple examples, the sequence of feedbacks operators solving the finite
dimensional LQR is not convergent. Roughly speaking this means that by refining the mesh we obtain a closed loop system which is not exponentially stable (even if the corresponding infinite
dimensional system is theoretically stabilized). In order to overcome this difficulty, several methods have been proposed in the literature : filtering of high frequencies, multigrid methods or
the introduction of a numerical viscosity term. We intend to first apply the numerical viscosity method introduced in Tcheougoué Tebou – Zuazua
New Results
Analysis and control of fluids and of fluid-structure interactions
Séverine
Baillet
Thomas
Chambrion
Antoine
Henrot
Jean
Houot
Alexandre
Munnier
Lionel
Rosier
Jean-François
Scheid
Mario
Sigalotti
Takéo
Takahashi
Jean-Baptiste
Tavernier
Marius
Tucsnak
Jean-Claude
Vivalda
Navier-Stokes equations
Korteweg de Vries equations
A part of our activity in this field has been devoted to the study of well-posedness and to the numerical analysis of the equations modeling the motion of rigid bodies in an incompressible
fluid. An important part of this work is done in collaboration with a group from the University of Chile through the associated team ANCIF. Many of the works we are quoting in what follows have
been done with a member of this group (Jorge San Martín, Jaime Ortega, Carlos Conca, Patricio Cumsille).
Concerning the well-posedness results, the last main achievements are reported in the papers
In the last year, we have started to study the motion of aquatic organisms. More precisely, in
Since September 2006, an INRIA associated engineer has been recruited to improve the current numerical code, to rewrite it in the Matlab software and finally to develop a 3D software for the
fish-like swimming. The improvement of the 2D code is in progress and deals with the Navier-Stokes solver together with the optimization of the Matlab implementation of the numerical code. The
Navier-Stokes solver has to allow to tackle realistic situations where the Reynolds number lies between
10
3and
10
6, depending on the nature of the fish-like swimming we consider (trout, salmon, eel, ...). The development of the 3D software has not started yet.
In
Another control problem has been obtained by Takahashi (in collaboration with Imanuvilov) for a fluid–structure system (
The same problem may be tackled with a perfect fluid (not necessarily potential), the normal component of the fluid velocity being controlled on a small part of the boundary. For a ball in
2D, it has been shown by Rosier that we may control the position of the ball, the ball being at rest at the beginning and at the end of the control process. The extension to a solid with one
axial symmetry (boat) is under investigation with Glass (Paris 6).
Another situation which has been treated is that of a rigid body moving in an inviscid fluid. More precisely, Chambrion and Sigalotti studied the controllability properties of a neutrally
buoyant underwater vehicle immersed in an infinite volume of an inviscid incompressible fluid in irrotational motion (see
Another quite different problem in fluid-structure interaction comes from the industrial PhD thesis of S. Baillet. At the end of the exploitation of an oil well, surface pumps are no longer
efficient enough to extract the oil remaining in the reservoir. Instead of closing the well, oil companies generally use well–pumps, introduced deep into the ground in order to maintain the
production. Such pumps are composed of a succession of identical stages (typically 15–20 stages, but it could go up to 100 stages) arranged in series. The optimization process needs numerical
simulation, but representing the whole pump numerically is impossible (for obvious calculation costs). Thus it is necessary to simplify the model, by representing only one stage. Therefore, a
very natural question which arises is the following: does the flow in one standard stage of the pump looks like the one we would obtain by considering periodic boundary conditions at the
entrance and the exit of the stage. Of course, one cannot hope that this kind of result holds for the first and the last stages which are still influenced by the boundary conditions at the top
and the bottom of the pump. Baillet, Henrot and Takahashi
Frequency tools for the analysis of
pde's
Bruno
Pinçon
Karim
Ramdani
Lionel
Rosier
Takéo
Takahashi
Marius
Tucsnak
Control and stabilization of systems governed by PDE's and their numerical approximation
It is well–known that the solution of LQR optimal control problems is given through a feedback operator involving a Riccati operator
P. This operator solves a Riccati equation in infinite dimension. Of course, in practice, one can only determine an approximate solution
Phof this equation, and the natural question that arises is the following : does the approximate solution obtained using this operator
Ph(instead of
P) converge to the solution of the continuous problem? This question has been so far studied by many authors (see for instance
h. Unfortunately, most of the standard numerical methods (finite element or finite differences) do not fulfill this condition. Using the frequency characterization of stabilizability
proposed by Liu and Zheng in
In
In
Acoustics
Time Reversal :In
Tis self-adjoint and compact. The D.O.R.T method (French acronym for Decomposition of the Time Reversal Operator) is explored numerically. In particular, we show that selective
focusing, which is known to occur for small and distant enough scatterers, holds when the wavelength and the size of these scatterers are of the same order of magnitude (medium frequency
situation). Moreover, we present the behavior of the eigenvalues of
Taccording to the frequency and we show their oscillations due to the interactions between the mirror and the obstacles and between the obstacles themselves.
In
Multiple scattering :In
Photonic crystals :In
The above results on time reversal and photonic crystals, added to other contributions on control of PDE's constitute the material of the “Habilitation à Diriger des Recherches” of Karim
Ramdani (see
Numerical methods for high-frequency scattering problems using microlocal analysis
In
Observability, controllability and stabilization in the time domain
Fatiha
Alabau
Antoine
Henrot
Mario
Sigalotti
Marius
Tucsnak
Jean-Claude
Vivalda
In
In
The results have been essentially used in
We have also obtained some results on the stabilization for visco-elastic materials. In many mechanical applications, the damping effects of materials are non-local and of memory type. It is
therefore important to obtain asymptotic properties of solutions as time grows, to know for instance for applications, if undesired vibrations of solutions will asymptotically decrease for
large time. For such materials, the solutions are described by hyperbolic PDE's, for which the feedback law is of memory type, which means that the feedback operator is a convolution operator
in time, therefore nonlocal (in time). One of the difficulty is that for such problems, the invariance by translation in time is lost, as well as the Lasalle invariance principle. Also,
dissipation properties and multiplier method is more involved. This leads to many challenging open questions. In the paper
Damping and stabilization properties of materials are an important field in control theory. In many applications, such damping phenomenas are highly nonlinear and the way of decay of the
feedback is not necessarily known. In
Henrot and Cox were interested in a musical problem which strongly use the eigenfrequency of the damped wave equation. It is a question relating to a model for harmonics on stringed
instruments which could be set as: is it possible to achieve “Correct Touch” in the pointwise damping of a fixed string? By correct touch, we consider the following. When we place a finger
lightly at one of the nodes of the low frequency harmonics, it forces the string to play a note that sounds like a superposition of those normal modes with nodes at the location of the finger.
Now, the question is to determine what should be the pressure of the finger in order to best damps the remaining modes. From a mathematical point of view, we consider the wave equation with a
damping as
b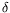
autwhere
utis the speed,
athe location of the pressure,
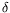
ais the Dirac distribution at
aand
bthe intensity of the pressure. We want to determine, for each
a, the
bwhich minimizes the spectral abscissa of the modes not vanishing at
a. This involves a precise qualitative analysis of the spectrum of the damped operator in the complex plane. This work will appear in
In
In
In
The observability of discrete time systems has been studied by Vivalda in

We show that a system which is observable with respect to the unknown input can be put into triangular form. Moreover, for this kind of systems, we design a practical
observer, that is to say a family of auxiliary dynamical system written as

such that

with
 and
and
 .
.
Biology and Medicine
Nicolae
Cîndea
Antoine
Henrot
Yannick
Privat
Marius
Tucsnak
A relatively recent activity of our group consists in proposing new methods for the reconstruction of moving objects via Magnetic Resonance Imaging (MRI). This is the main topic of the Phd
thesis of Cîndea, which is directed jointly by Tucsnak and Vuissoz from the MRI laboratory of the University Hospital of Nancy. One ideas of this works is to use the theory of observers in
order to reconstruct the state from the measurements in the Fourier space. This work is based on solving preliminary modeling and identification problems which require computations which
cannot, for the moment, be performed in real time. These problems are tackled by our group by two methods. The first one, presented in a paper submitted to
MRMreduces the problem to an integral equation which is solved using a regularization procedure. This method is based on the fact that the motion of the moving body has been partially
detected by appropriate sensors.
The second method uses weaker information on the motion of the body, namely that it is periodic. The aim of our work is to provide a method for cardiac imaging reconstruction at each cardiac
or respiratory phase. We propose a method inspired by Zwaan
In the paper
is the dichotomic structure of the lung tree and the dimension of each branch optimal?
is the cylindrical shape of a given branch optimal?
![]() estimates we get allow us to describe the asymptotic trajectory of the center of mass of the rigid body as well.
estimates we get allow us to describe the asymptotic trajectory of the center of mass of the rigid body as well.![]() type. Obtaining the similar tools for systems governed by PDE's is one of the major challenges in the theory of infinite dimensional systems. The first difficulty which has to be
tackled is that, even for very simple PDE systems, no method giving the parametrisation of all stabilizing controllers is available. One of the possible remedies consists in considering known
families of stabilizing feedback laws depending on several parameters and in optimizing the
type. Obtaining the similar tools for systems governed by PDE's is one of the major challenges in the theory of infinite dimensional systems. The first difficulty which has to be
tackled is that, even for very simple PDE systems, no method giving the parametrisation of all stabilizing controllers is available. One of the possible remedies consists in considering known
families of stabilizing feedback laws depending on several parameters and in optimizing the
![]() norm of an appropriate transfer function with respect to this parameters. Such families of feedback laws yielding computationally tractable optimization problems are now available for
systems governed by PDE's in one space dimension.
norm of an appropriate transfer function with respect to this parameters. Such families of feedback laws yielding computationally tractable optimization problems are now available for
systems governed by PDE's in one space dimension.