Overall Objectives
Highlights of the year
Concerning research, a lot of effort has been put this year in the study of Lévy processes in financial modelling with significant contributions in numerical methods for option pricing and
control.
Concerning staff, the main evolution in 2007 is the recruiting of Aurélien Alfonsi at ENPC/Cermics in the probability team. He is joining the Mathfi team in September 2007 after spending one
academic year as a postdoc in the technical university of Berlin supervised by Alexander Schied. Moreover Marie-Claire Kammerer-Quenez, formely assistant-professor at the University of
Marne-la-Vallée has been recruted as a professor at the Universty Paris-Diderot (Paris 7).
Introduction
MathFi is a joint INRIA project-team with ENPC (CERMICS) and the University of Marne la Vallée, located in Rocquencourt and Marne la Vallée.
The development of increasingly complex financial products requires the use of advanced stochastic and numerical analysis techniques. The scientific skills of the MathFi research team are
focused on probabilistic and deterministic numerical methods and their implementation, stochastic analysis, stochastic control. Main applications concern evaluation and hedging of derivative
products, dynamic portfolio optimization in incomplete markets, calibration of financial models. Special attention is paid to models with jumps, stochastic volatility models, asymmetry of
information. The MathFi project team develops the software Premia dedicated to pricing and hedging options and calibration of financial models, in collaboration with a consortium of financial
institutions. Premia web Site:
[http://
www.
premia.
fr].
Scientific Foundations
Numerical methods for option pricing and hedging
all the Mathfi
team
Monte-Carlo
Euler schemes
approximation of SDE
tree methods
Malliavin calculus
finite difference
Efficient computations of prices and hedges for derivative products is a major issue for financial institutions.
Monte-Carlo simulations are widely used because of their implementation simplicity and because closed formulas are usually not available. Nevertheless, efficiency relies on difficult
mathematical problems such as accurate approximation of functionals of Brownian motion (e.g. for exotic options), use of low discrepancy sequences for nonsmooth functions, quantization methods
etc. Speeding up the algorithms is a constant preoccupation in the developement of Monte-Carlo simulations. Another approach is the numerical analysis of the (integro) partial differential
equations which arise in finance: parabolic degenerate Kolmogorov equation, Hamilton-Jacobi-Bellman equations, variational and quasi–variational inequalities (see
This activity in the MathFi team is strongly related to the development of the Premia software.
Model calibration
A important research direction in mathematical finance is the modeling of the so called
implied volatility smile, that is, the fact that different traded options on the same underlying have different Black-Scholes implied volatilities. The smile phenomenon clearly indicates
that the Black-Scholes model with constant volatility does not provide a satisfactory explanation of the prices observed in the market and has led to the appearance of a large variety of
extensions of this model aiming to overcome the above difficulty. Some popular model classes are: the local volatility models (where the stock price volatility is a deterministic function of
price level and time), diffusions with stochastic volatility, jump-diffusions, and so on. An essential step in using any such approach is the
model calibration, that is, the reconstruction of model parameters from the prices of traded options. The main difficulty of the calibration problem comes from the fact that it is an
inverse problem to that of option pricing and as such, typically ill-posed.
The calibration problem is yet more complex in the interest rate markets since in this case the empirical data that can be used includes a wider variety of financial products from standard
obligations to swaptions (options on swaps). The underlying model may belong to the class of short rate models like Hull-White
The choice of a particular model depends on the financial products available for calibration as well as on the problems in which the result of the calibration will be used.
The calibration problem is of particular interest for MathFi project because due to its high numerical complexity, it is one of the domains of mathematical finance where efficient
computational algorithms are most needed.
Malliavin calculus and applications in finance
V.
Bally
B.
Jourdain
A.
Kohatsu-Higa
D.
Lamberton
B.
Lapeyre
A.
Sulem
A.
Zanette
Malliavin calculus
stochastic variations calculus
sensibility calculus
greek computations
The original Stochastic Calculus of Variations, now called the Malliavin calculus, was developed by Paul Malliavin in 1976
From the beginning of the nineties, applications of the Malliavin calculus in finance have appeared : In 1991 Karatzas and Ocone showed how the Malliavin calculus, as further developed by
Ocone and others, could be used in the computation of hedging portfolios in complete markets
Since then, the Malliavin calculus has raised increasing interest and subsequently many other applications to finance have been found
Let us try to give an idea why Malliavin calculus may be a useful instrument for probabilistic numerical methods. We recall that the theory is based on an integration by parts formula of the
form
E(
f'(
X)) =
E(
f(
X)
Q). Here
Xis a random variable which is supposed to be “smooth” in a certain sense and non-degenerated. A basic example is to take
X=
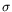
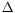 where
where
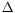 is a standard normally distributed random variable and
is a standard normally distributed random variable and
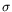 is a strictly positive number. Note that an integration by parts formula may be obtained just by using the usual integration by parts in the presence of the Gaussian density. But we may
go further and take
is a strictly positive number. Note that an integration by parts formula may be obtained just by using the usual integration by parts in the presence of the Gaussian density. But we may
go further and take
Xto be an aggregate of Gaussian random variables (think for example of the Euler scheme for a diffusion process) or the limit of such simple functionals.
An important feature is that one has a relatively explicit expression for the weight
Qwhich appears in the integration by parts formula, and this expression is given in terms of some Malliavin-derivative operators.
Let us now look at one of the main consequenses of the integration by parts formula. If one considers the
Diracfunction
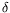
x(
y), then
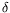
x(
y) =
H'(
y-
x)where
His the
Heavisidefunction and the above integration by parts formula reads
E(
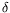
x(
X)) =
E(
H(
X-
x)
Q),where
E(
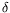
x(
X))can be interpreted as the density of the random variable
X. We thus obtain an integral representation of the density of the law of
X. This is the starting point of the approach to the density of the law of a diffusion process: the above integral representation allows us to prove that under appropriate hypothesis the
density of
Xis smooth and also to derive upper and lower bounds for it. Concerning simulation by Monte Carlo methods, suppose that you want to compute
 where
where
X1, ...,
XMis a sample of
X. As
Xhas a law which is absolutely continuous with respect to the Lebesgue measure, this will fail because no
Xihits exactly
x. But if you are able to simulate the weight
Qas well (and this is the case in many applications because of the explicit form mentioned above) then you may try to compute
 This basic remark formula leads to efficient methods to compute by a Monte Carlo method some irregular quantities as derivatives of option prices with respect to some parameters (the
Greeks) or conditional expectations, which appear in the pricing of American options by the dynamic programming). See the papers by Fournié et al
This basic remark formula leads to efficient methods to compute by a Monte Carlo method some irregular quantities as derivatives of option prices with respect to some parameters (the
Greeks) or conditional expectations, which appear in the pricing of American options by the dynamic programming). See the papers by Fournié et al
More recently the Malliavin calculus has been used in models of insider trading. The "enlargement of filtration" technique plays an important role in the modeling of such problems and the
Malliavin calculus can be used to obtain general results about when and how such filtration enlargement is possible. See the paper by P.Imkeller in
Anticipative stochastic calculus and insider trading
A.
Kohatsu-Higa
A.
Sulem
We study controlled stochastic systems whose state is described by anticipative stochastic differential equations. These SDEs can interpreted in the sense of
forward integrals, which are the natural generalization of the semimartingale integrals
Stochastic Control and Backward Stochastic Differential equations
V.
Bally
J.-Ph.
Chancelier
M.C.
Kammerer-Quenez
A.
Sulem
Stochastic Control
singular and impulse control
risk-sensitive control
free boundary
Hamilton-Jacobi-Bellman
variational and quasi-variational inequalities
BSDE
Stochastic control consists in the study of dynamical systems subject to random perturbations and which can be controlled in order to optimize some performance criterion. Dynamic programming
approach leads to Hamilton-Jacobi-Bellman (HJB) equations for the value function. This equation is of integrodifferential type when the underlying processes admit jumps (see
New Results
Numerical methods for option pricing
A.
Alfonsi
B.
Jourdain
C.
Labart
J.
Lelong
A. Alfonsi and B. Jourdain are working on duality for American options. In
J. Lelong and C. Labart are working on the pricing of double barrier Parisian options using Laplace transforms (see
Discretization of stochastic differential equations
A.
Alfonsi
B.
Jourdain
M.
Sbai
A. Alfonsi has started to work on the discretization of the Cox-Ingersoll-Ross process. This SDE presents a singularity that makes its discretization non standard. Many schemes had been
proposed in the literature, but most of them were really satisfactory only for small volatility parameters (
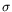 2
2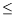 4
4
a). In
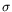 2>0: a quadratic weak convergence in function of the time-step is shown. Then, using the Ninomiya-Victoir approach, he applies this scheme to the widespread Heston model
(for which large volatility parameters are observed) and gets interesting results.
2>0: a quadratic weak convergence in function of the time-step is shown. Then, using the Ninomiya-Victoir approach, he applies this scheme to the widespread Heston model
(for which large volatility parameters are observed) and gets interesting results.
A method allowing exact simulation of the solution of one-dimensional stochastic differential equations has been recently proposed by Beskos and Roberts
Existing weak convergence results for discretization schemes of SDEs are not adapted to deal with the payoffs of exotic options which involve the whole sample-path of the underlying. M. Sbai
and B. Jourdain are trying to analyse the convergence properties for better suited criteria such as the Vasertein distance on the sample-path space.
Monte Carlo simulations and stochastic algorithms
V.
Bally
E.H.A.
Dia
B.
Jourdain
C.
Labart
D.
Lamberton
B.
Lapeyre
J.
Lelong
Monte-Carlo
variance reduction
Variance reduction by adaptive stratified sampling
The stratified sampling technique consists in computing the expectation of a random variable as a sum over strata which form a partition of the state space. The contribution of each
stratum is the product of the probability for the random variable to belong to this stratum by the expectation of the random variable conditioned to belong to the stratum. The probabilities
are known explicitely whereas the conditional expectations are computed by the Monte Carlo method.
In this approach, the probability of each stratum has to be known analytically and simulation according to the corresponding conditional law must be feasible. It is well-known that
allocation of the numbers of random drawings in the strata proportional to their probability achieves variance reduction. But the optimal allocation which involves the conditional variances
in the strata is unknown. For fixed strata, P. Etoré (postdoc at ENPC) and B. Jourdain have developped an algorithm aimed at adaptively estimating the optimal allocation of the drawings
between the strata when computing the stratified Monte-Carlo estimator of the expectation. For their estimator, they prove a central limit theorem with asymptotic variance equal to the
optimal variance and confirm its performance by numerical experiments
Monte-Carlo methods for exotic options in models with jumps
D. Lamberton and his phD student El Hadj Aly DIA's have obtained some results concerning lookback options in jump-diffusion models.
Backward Stochastic Differential equations (BSDEs)
C. Labart has defended her thesis on October, 2007 and arrived immediatly after for a postdoctoral position in Mathfi. She is presently implementing in Premia a numerical algorithm for
solving BSDEs, based on Picard's procedure and a sequential Monte Carlo method. She is also working with V. Bally on a slightly different algorithm, using Malliavin calculus techniques, for
solving BSDEs.
Computation of sensitivities and conditional expectations using Malliavin calculus in models with jumps
V.
Bally
M.P.
Bavouzet
A.
Kohatsu-Higa
M.
Messaoud
N.
Privault
X.
Wei
A.
Zanette
Malliavin calculus
greeks
V. Bally, M.P. Bavouzet and M. Messaoud are working on Malliavin Calculus for Poisson Point Processes and applications to finance. A paper will appear in Annals of Applied Probability
Anticipative stochastic calculus in model with jumps
A.
Kohatsu-Higa
A.
Sulem
anticipative calculus
forward integrals
insider
asymmetry information
A.Kohatsu-Higa and A.Sulem are working on the extension of their paper on insider trading
A. Sulem and B. Øksendal propose an anticipative approach for indifference pricing in incomplete markets
Lower bounds for the density of a functional
V.
Bally
A. Kohatsu
Higa
V. Bally has three projects on this subject in progress, in collaboration with: B. Fernandez and A. Meda from the University of Mexico, in collaboration with L. Caramellino from the
University of Roma 3 and finally in collaboration with A. Kohasu-Higa.
Optimal stopping and American Options
D.
Lamberton
M.
Mikou
Damien Lamberton and Mihail Zervos (previously at King's College, London, now at the London School of Economics) have extended previous results on optimal stopping of one-dimensional
diffusions for infinite horizon to finite horizon. In
D. Lamberton and his PhD student Mohammed Mikou have studied some properties of the exercise boundary of the American put option in an exponential Lévy model (continuity of the exercise
boundary, behavior near maturity). A paper has been submitted
Sparse grids methods for PDEs
Y.
Achdou
D.
Pommier
A.
Sulem
sparse grids
finite element
adaptive finite elements
lattice-based methods
Recent developments have shown that it may be possible to use deterministic Galerkin methods or grid based methods for elliptic or parabolic problems in dimension
d, for
4
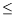
d
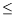 10: these methods are based either on sparse grids
10: these methods are based either on sparse grids
Sparse grids were introduced by Zenger
d-linear sparse grid approximation requires only
 degrees of freedom instead of
degrees of freedom instead of
O(
h-
d)for the standard piecewise linear approximations (
his the mesh step).
D. Pommier has studied these methods for the numerical solution of diffusion or advection-diffusion problems introduced in option pricing. He considers European vanilla contracts in multi
factor stochastic volatility models (3 factors) and compares the numerical approximation obtained by Wavelet Galerkin method and Finite Difference method for the parabolic equation and the
Integro-Differential Equations in a jump diffusion model. For the integral-operator, he proposes a collocation method adapted to the sparse grid discretization.
Stochastic control of jump diffusions and applications
M.
Arizawa
A.
Sulem
jump diffusions
stochastic control
B. Øksendal (Oslo University) and A.Sulem have written a second edition of their book on Stochastic control of Jump diffusions
In
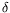 >0between the time when a decision for intervention is taken and the time when
the intervention is actually carried out. They show that under certain conditions this problem can be transformed into a sequence of iterated no-delay optimal stopping problems and there is an
explicit relation between the solutions of these two problems.
>0between the time when a decision for intervention is taken and the time when
the intervention is actually carried out. They show that under certain conditions this problem can be transformed into a sequence of iterated no-delay optimal stopping problems and there is an
explicit relation between the solutions of these two problems.
In
Mariko Arizawa is studying homogenization with the Lévy operators. She has established the equivalent relationship between various definitions of viscosity solutions
Risk measures and applications
M.C
Quenez
A.
Sulem
risk measures
BSDE
A. Sulem and B. Øksendal have studing risk-indifference pricing in incomplete markets: They define the (seller's)
risk indifference price
priskselleras the initial payment that makes the
riskinvolved for the seller of a contract equal to the risk involved if the contract is not sold, with no initial payment. In the case of jump diffusions models, using stochastic control
theory and PDE methods, they find a formula for
prisksellerand similarly for
priskbuyer. In particular, they prove that
plow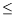
priskbuyer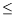
priskseller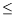
pup, where
plowand
pupare the lower and upper hedging prices, respectively.
M.C. Quenez and Daniel Hernandez-Hernandez (Cimat, Mexico) are studying the problem of characterizing the variance optimal martingale measure
 in a stochastic volatility model. Recall that the variance-optimal martingale measure appears to be a key tool for characterizing the optimal hedging strategy of the mean-variance
hedging problem. Laurent and Pham (1999) have solved the problem in terms of classical solutions of PDEs in the particular case where the coefficients of the model do not depend on time and
price process (they only depend on
in a stochastic volatility model. Recall that the variance-optimal martingale measure appears to be a key tool for characterizing the optimal hedging strategy of the mean-variance
hedging problem. Laurent and Pham (1999) have solved the problem in terms of classical solutions of PDEs in the particular case where the coefficients of the model do not depend on time and
price process (they only depend on
Ytthe state process). Quenez and Hernandez-Hernandez consider the general case where the coefficients depend on
Yt, on time
tand on price
St.
M.C. Quenez is studying how some dynamic measures of risk can be induced by Backward Stochastic Differential Equations (BSDEs).
Contracts and Grants with Industry
Consortium Premia
A.
Alfonsi
V.
Bally
B.
Jourdain
A.
Kohatsu-Higa
B.
Lapeyre
J.
Lelong
N.
Privault
A.
Sulem
A.
Zanette
The consortium Premia is centered on the development of the pricer software Premia. It is presently composed of the following financial institutions or departments: CALYON, the Crédit
Industriel et Commercial, Société Générale, Natexis and IXIS CIB now unifies as Natixis.
[http://
www.
premia.
fr]
Extension to Japan has been realized via a cooperation with the university of Osaka.
[http://www-csfi.sigmath.es.osaka-u.ac.jp/premia/index.html]. Similar
procedure is ongoing with Hong Kong City university.
BNP-Paribas
D.
Pommier
Y.
Achdou
A.
Sulem
Cifre agreement BNP-Paribas/INRIA on : "sparse grids for large dimensional financial issues”
EuroVL
M.
Hamel
N.
Privault
A.
Sulem
Cifre agreement between Euro-VL and INRIA on “ Pricing of hybrid financial derivative products on change and interest rate “.
ANR program
ANR program GCPMF "Grid Computation for Financial Mathematics" (partners : Calyon, Centrale, EDF, ENPC, INRIA, Ixis, Paris 6, Pricing Partner, Summit, Supelec)
Global coordinator: B. Lapeyre
Participation to the proposal “Creditnext” on credit risk derivatives.
International cooperations
Part of the European network "Advanced Mathematical Methods for Finance" (AMaMef). This network has received approval from the European Science Foundation (ESF).
Programme Sakura-Ayame with Osaka University.
Cooperations with Osaka university and ongoing cooperation with Hong Kong city university for extension of the Premia consortium.
Collaborations with the Universities of Oslo, Bath, Chicago, Mexico, Osaka, Rome II and III, Tokyo Institute of Technology
![]()
![]() where
where
![]() is a standard normally distributed random variable and
is a standard normally distributed random variable and
![]() is a strictly positive number. Note that an integration by parts formula may be obtained just by using the usual integration by parts in the presence of the Gaussian density. But we may
go further and take
is a strictly positive number. Note that an integration by parts formula may be obtained just by using the usual integration by parts in the presence of the Gaussian density. But we may
go further and take
![]()
![]()
![]()
![]()
![]() where
where
![]() This basic remark formula leads to efficient methods to compute by a Monte Carlo method some irregular quantities as derivatives of option prices with respect to some parameters (the
Greeks) or conditional expectations, which appear in the pricing of American options by the dynamic programming). See the papers by Fournié et al
and
and the papers by Bally et al, Benhamou, Bermin et al., Bernis et al., Cvitanic et al., Talay and Zheng and Temam
in
.
This basic remark formula leads to efficient methods to compute by a Monte Carlo method some irregular quantities as derivatives of option prices with respect to some parameters (the
Greeks) or conditional expectations, which appear in the pricing of American options by the dynamic programming). See the papers by Fournié et al
and
and the papers by Bally et al, Benhamou, Bermin et al., Bernis et al., Cvitanic et al., Talay and Zheng and Temam
in
.