Rewriting Calculus
rewriting
strategies
types
rewriting calculus
graph rewriting
The rewriting calculus, studied in our team since 1996, is a foundational framework unifying rewriting and lambda-calculus. We have now a deep understanding of its agility and properties,
culminating this year with the PhD thesis of Germain Faure and refinements on the graph versions of the calculus, the relationship between the calculus and higher-order rewritings, as well as
the in depth study of its typed versions.
Confluence of Pattern-Based Calculi
Horatiu
Cirstea
Germain
Faure
Different pattern calculi integrate the functional mechanisms from the
 -calculus and the matching capabilities from rewriting. Several approaches are used to obtain the confluence but in practice the proof methods share the same structure and each
variation on the way pattern-abstractions are applied needs another proof of confluence.
-calculus and the matching capabilities from rewriting. Several approaches are used to obtain the confluence but in practice the proof methods share the same structure and each
variation on the way pattern-abstractions are applied needs another proof of confluence.
We have proposed in
Our approach directly applies to different pattern calculi, namely the lambda calculus with patterns, the pure pattern calculus and the rewriting calculus. We also characterized a class of
matching algorithms and consequently of pattern-calculi that are not confluent.
Canonical sets of terms
Horatiu
Cirstea
Germain
Faure
Claude
Kirchner
Term collections are fundamental in the context of the rewriting calculus but also in logic programming and in web query languages. Typically, matching constraints that are involved in the
rewriting calculus may have more than one solution (this is also the case for example in programming language like
Tom, Maude, ASF+SDF or
ELAN) and thus generates a collection of results.
As a first step in the study of the rewriting calculus with non-unitary matching theories, we studied the lambda-calculus with term collections
In the spirit of normalized rewriting
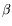 -rule is an explicit evaluation step. While the work of Boudol
-rule is an explicit evaluation step. While the work of Boudol
Explicit
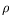 -calculus
Horatiu
Cirstea
Germain
Faure
Claude
Kirchner
-calculus
Horatiu
Cirstea
Germain
Faure
Claude
Kirchner
Following the works on explicit substitutions for
 -calculus, we proposed, studied and exemplified
-calculus, we proposed, studied and exemplified
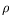 -calculus that handles explicitly the resolution of the matching constraints and the application of the obtained substitutions. We have also shown that the approach is modular and we
have introduced a calculus handling explicitly only the substitution application and another one where the matching constraints are solved at the object level while the resulting
substitutions are applied at the meta-level
-calculus that handles explicitly the resolution of the matching constraints and the application of the obtained substitutions. We have also shown that the approach is modular and we
have introduced a calculus handling explicitly only the substitution application and another one where the matching constraints are solved at the object level while the resulting
substitutions are applied at the meta-level
The explicit substitution application initially studied
Moreover, in this approach the matching constraints with no solution can be eliminated earlier in the reduction process leading to a more efficient evaluation. This can be achieved by
integrating in the explicit calculus the approach already used for the plain calculus
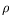 -Calculus and Combinatory Reduction Systems
Horatiu
Cirstea
Claude
Kirchner
-Calculus and Combinatory Reduction Systems
Horatiu
Cirstea
Claude
Kirchner
Since
 -calculus and rewriting have complementary features, their combination has been studied in different contexts. We have already shown that
-calculus and rewriting have complementary features, their combination has been studied in different contexts. We have already shown that
 -calculus and rewriting are generalized by the
-calculus and rewriting are generalized by the
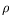 -calculus, in the sense that the syntax and the inference rules of the
-calculus, in the sense that the syntax and the inference rules of the
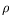 -calculus can be restricted to obtain the other two formalisms.
-calculus can be restricted to obtain the other two formalisms.
In the prolongation of our works on the expressive power of the
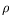 -calculus we have analyzed with Clara Bertolissi from the University Aix-Marseille 1, the relation between
-calculus we have analyzed with Clara Bertolissi from the University Aix-Marseille 1, the relation between
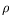 -calculus and higher order rewriting. We had showed how the semantics of Combinatory Reduction Systems can be expressed in terms of the rewriting calculus. The converse issue has been
addressed lately: rewriting calculus derivations are simulated by Combinatory Reduction Systems derivations. As a consequence of this result, important properties, like standardisation, are
deduced for the rewriting calculus
-calculus and higher order rewriting. We had showed how the semantics of Combinatory Reduction Systems can be expressed in terms of the rewriting calculus. The converse issue has been
addressed lately: rewriting calculus derivations are simulated by Combinatory Reduction Systems derivations. As a consequence of this result, important properties, like standardisation, are
deduced for the rewriting calculus
Sharing strategy for the graph rewriting calculus
Horatiu
Cirstea
Claude
Kirchner
Starting from the classical untyped
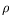 -calculus and in collaboration with Paolo Baldan from the University of Venice and Clara Bertolissi from the University Aix-Marseille 1, we have proposed an extension of the calculus,
called
graph rewriting calculus, handling structures containing sharing and cycles, rather than simple terms
-calculus and in collaboration with Paolo Baldan from the University of Venice and Clara Bertolissi from the University Aix-Marseille 1, we have proposed an extension of the calculus,
called
graph rewriting calculus, handling structures containing sharing and cycles, rather than simple terms
The classical
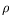 -calculus is naturally generalized by considering lists of constraints containing unification constraints in addition to the standard matching constraints. This leads to a term-graph
representation in an equational style where terms consist of unordered lists of constraints. As for the classical
-calculus is naturally generalized by considering lists of constraints containing unification constraints in addition to the standard matching constraints. This leads to a term-graph
representation in an equational style where terms consist of unordered lists of constraints. As for the classical
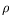 -calculus, the transformations are performed by explicit application of rewrite rules as first class entities.
-calculus, the transformations are performed by explicit application of rewrite rules as first class entities.
The evaluation rules are adapted to the new syntax leading to an enhanced expressive power for the calculus. In this new formalism we can represent and manipulate elaborated objects like,
for example, regular infinite entities.
Several aspects of the calculus have been investigated so far, like its properties (we have also shown that the calculus is confluent over equivalence classes of terms, under some
linearity restrictions on patterns) and its relationship with other existing frameworks.
We have proposed lately
A Rewriting Calculus for Multigraphs with Ports
Oana
Andrei
Hélène
Kirchner
In
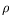
mg-calculus.
Distributive rewriting calculus
Horatiu
Cirstea
Clément
Houtmann
General term rewriting systems and classical guiding strategies have been encoded in the original rewriting calculus
In collaboration with Benjamin Wack, we have shown that the previously proposed encoding can be extended to the general case, i.e. to arbitrary term rewrite systems
Implementation techniques for the Rewriting Calculus
Horatiu
Cirstea
Germain
Faure
We used the
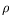 -calculus as an intermediate language to compile functional languages with pattern-matching features, and adapt the evaluation strategies developed for the
-calculus as an intermediate language to compile functional languages with pattern-matching features, and adapt the evaluation strategies developed for the
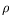 -calculus to the specific constraints arising from typed functional programs.
-calculus to the specific constraints arising from typed functional programs.
In
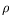 -calculus in interaction nets
-calculus in interaction nets
 -calculus). In collaboration with Maribel Fernandez (King's College), Ian Mackie (CNRS and King's college) and François-Régis Sinot (University of Porto), we showed in
-calculus). In collaboration with Maribel Fernandez (King's College), Ian Mackie (CNRS and King's college) and François-Régis Sinot (University of Porto), we showed in
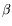 -reduction can proceed in parallel, without additional overheads. The compilation of functional programs in the
-reduction can proceed in parallel, without additional overheads. The compilation of functional programs in the
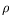 -calculus, and the subsequent interaction net encoding, uncover a new strategy of evaluation which naturally exploits the implicit parallelism of the different rules of the calculus.
This methodology gives thus rise to new, efficient strategies of evaluation for functional languages.
-calculus, and the subsequent interaction net encoding, uncover a new strategy of evaluation which naturally exploits the implicit parallelism of the different rules of the calculus.
This methodology gives thus rise to new, efficient strategies of evaluation for functional languages.
Strong Normalization of Pure Pattern Type Systems
Clément
Houtmann
Pure Pattern Type Systems
P2TS) combine in a unified setting the frameworks and capabilities of rewriting and
 -calculus. Their type systems, adapted from Barendregt's
-calculus. Their type systems, adapted from Barendregt's
 -cube, are especially interesting from a logical point of view. Strong normalization, an essential property for logical soundness, had only been conjectured so far.
-cube, are especially interesting from a logical point of view. Strong normalization, an essential property for logical soundness, had only been conjectured so far.
In strong collaboration with Benjamin Wack (now professeur agrégé de mathématiques), we have proved in
P2TS. The proof relies on a faithful translation from simply-typed
P2TSinto System
 , and then from dependently-typed
, and then from dependently-typed
P2TSinto simply-typed
P2TS.
In the untyped framework, we encoded pattern matching in the
 -calculus in a quite efficient way, ensuring that every
-calculus in a quite efficient way, ensuring that every
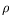
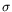
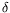 -reduction is translated into (at least) one
-reduction is translated into (at least) one
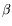 -reduction. Introducing types in the translation proved an interesting challenge. One difficulty comes from the pattern matching occurring in the
-reduction. Introducing types in the translation proved an interesting challenge. One difficulty comes from the pattern matching occurring in the
P2TStypes, which calls for accurate adjustments in the translation. Another remarkable point is that the typing mechanisms of even the simply-typed
P2TScan be expressed only with the expressive power of System
 , which is rather surprising since
, which is rather surprising since
 is a higher-order system featuring types depending on types.
is a higher-order system featuring types depending on types.
Rule-based programming
algebraic specification
abstract data-types
pattern matching
compilation
complexity analysis
We are studying the design and the implementation of rule-based programming languages. We modularize our technologies in order to make them available as separate elementary tools.
Several improvements have been designed in pattern matching with anti-patterns, structure sharing via graph rewriting, and through powerful strategies. Also, we continue our study on
applications of rule-based languages. In particular, we study their applications to XML transformations, biochemichal systems simulation, as well as the analysis and the certification of
program transformations and of access control policies.
Finally, the algebraic structure of polygraph has been used as a description of graphical rule-based computations, equipped with complexity analysis tools.
Strategic Programming in Java
Émilie
Balland
Paul
Brauner
Radu
Kopetz
Pierre-Etienne
Moreau
Antoine
Reilles
One interest of term rewriting is its ability to describe elementary transformations. When combined with a strategy language it becomes very expressive to describe complex transformations.
Starting from the
ELANexperience, we have provided a powerful strategy language, that can be easily integrated in a Java environment. This language, which is part of the
Tomsystem is presented in
Anti-Pattern Matching
Claude
Kirchner
Radu
Kopetz
Pierre-Etienne
Moreau
Pattern matching is a concept widely spread both in computer science community and in everyday life. Whenever we search for something, we build a structured object, a pattern, that
specifies the features we are interested in. But we are often in the case where we want to exclude certain characteristics: typically we would like to specify that we search for white cars
that are not station wagons, or to words that do not contain the letter “a”.
To this end, we have defined in
A natural question that then raises is to deal with anti-pattern when some of the symbols have some equational properties. To answer this question, we generalized in
E, and we study the specific and practically very useful case of associativity, possibly with a unity (
 ). To this end, based on the
syntacticnessof associativity, we present a rule-based associative matching algorithm, and we extend it to
). To this end, based on the
syntacticnessof associativity, we present a rule-based associative matching algorithm, and we extend it to
 . This algorithm is then used to solve
. This algorithm is then used to solve
 anti-pattern matching problems. This allows us to be generic enough so that for instance, the
AllDiffstandard predicate of constraint programming becomes simply expressible in this framework.
anti-pattern matching problems. This allows us to be generic enough so that for instance, the
AllDiffstandard predicate of constraint programming becomes simply expressible in this framework.
 anti-patterns are implemented in the
Tomlanguage and we show some examples of their usage. An extended version of this work is available as a research report
anti-patterns are implemented in the
Tomlanguage and we show some examples of their usage. An extended version of this work is available as a research report
Bytecode rewriting
Émilie
Balland
Pauline
Kouzmenko
Pierre-Etienne
Moreau
Antoine
Reilles
There exist several libraries for manipulating Java bytecode, among them BCEL and ASM are the most well-known. Although they are powerful, a deep knowledge of the API may be needed to use
them effectively.
We introduce an abstraction level, based on term-rewriting, to make the definition of high-level transformations and analysis easier. Using the notion of algebraic view, we have extended
the ASM library in such a way that a bytecode program can be seen as a term
Term graph rewriting
Émilie
Balland
Paul
Brauner
Claude
Kirchner
Pierre-Etienne
Moreau
Program transformation and graph rewriting are strongly related. Indeed, although the structure of a program may be represented by a tree, informations about its execution like data
dependencies or control flow are naturally expressed by data-structures inherently using graphs. To manage such structures, we have generalized the notion of term positions with
term paths
Based on the formalization of paths and a notion of rewriting for addressed terms, we establish a simulation of term-graph rewriting by addressed terms. The main advantage of such an
approach is to offer an efficient way to implement in any rule-based language term-graph rewriting features. In fact, since the simulation is completely based on standard first-order terms,
this extension is non-intrusive. The integration in the
Tomlanguage provides a solid platform to experiment graph transformations in a concise and expressive way.
Rule-Based Modeling for Biochemical Applications
Oana
Andrei
Hélène
Kirchner
Providing a formal description for the structure and functioning of biochemical systems, as well as formal tools for reasoning about their behavior is yet a scientific challenge.
Frequently, the description of molecular complexes or chemical reactants relies on specific classes of graphs, and the interactions between the reactants involve rules applied on these
classes of graphs and controlled by numerical data or specific filters. In this context of biochemical systems, typical considered problems are the exhaustive generation of all possible
states of the system, the detection of specific states, or the prediction of producing specific states. In
In the biochemical model we consider, the behaviour of a protein is given by its functional domains that determine which other protein it can bind to or interact with. These domains are
usually abstracted as sites that can be bound or free, visible or hidden. A protein is characterized by the collection of interaction sites on its surface. Proteins can bind to each other
forming molecular complexes. Membranes can also form complexes, called tissues, due to the binding proteins on their surfaces. The structure of a complex is naturally described as an extended
version of multigraphs with ports
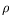
bio-calculus, obtained from the rewrite calculus for labeled multigraphs with ports, the
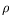
mg-calculus introduced in
Rewriting-Based Access Control Policies
Yassine
Guebbas
Claude
Kirchner
Hélène
Kirchner
Anderson
Santana
Eric
Ke Wang
Security policies, in particular access control, are fundamental elements of computer security. In collaboration with Dan Dougherty (Worcester Polytechnic Institute, USA) we have addressed
the problem of authoring and analyzing policies in a modular way using techniques developed in the field of term rewriting, focusing especially on the use of rewriting strategies. Term
rewriting supports a formalization of access control with a clear declarative semantics based on equational logic and an operational semantics guided by strategies. Well-established term
rewriting techniques allow us to check properties of policies such as the absence of conflicts and the property of always returning a decision. A rich language for expressing rewriting
strategies is used to define a theory of modular construction of policies, in which we can better understand the preservation of properties of policies under composition.
This framework is presented in
Despite the existence of a vast literature on access control, it is still very hard to assure the compliance of a large system to a given dynamic access control policy. Based on the formal
islands approach, we provided in
Another contribution in this domain, in collaboration with Charles Morisset (LIP6), has been to address the verification of information leakage. Although this important property is assumed
in several access control models and is well-understood formally, it is hard to verify in actual implementations of a given security policy. In
Quotient types in functional programming
Frédéric
Blanqui
Richard
Bonichon
Laura
Lowenthal
This work was done in collaboration with Thérèse Hardin (LIP6) and Pierre Weis (INRIA Paris - Rocquencourt).
Many algorithms use concrete data types with some additional invariants. The set of values satisfying the invariants is often a set of representatives for the equivalence classes of some
equational theory. For instance, a sorted list is a particular representative wrt commutativity. Theories like associativity, neutral element, idempotence, etc. are also very common. Now,
when one wants to combine various invariants, it may be difficult to find the suitable representatives and to efficiently implement the invariants. The preservation of invariants throughout
the whole program is even more difficult and error prone. Classically, the programmer solves this problem using a combination of two techniques: the definition of appropriate construction
functions for the representatives and the consistent usage of these functions ensured via compiler verifications. The common way of ensuring consistency is to use an abstract data type for
the representatives; unfortunately, pattern matching on representatives is lost. A more appealing alternative is to define a concrete data type with private constructors so that both compiler
verification and pattern matching on representatives are granted. In
Polygraphs as a computational model
Yves
Guiraud
Aurélien
Monot
Pierre-Etienne
Moreau
Polygraphs provide an algebraic structure to graphical computations. Introduced by Albert Burroni as a
n-categorical formalization of equational theories
With Guillaume Bonfante (Carte, LORIA and INRIA), we have defined polygraphic programs as a generalisation of first-order functional programs. Inspired by polynomial interpretations of
terms
n-category. These tools allowed us to give a new, polygraphic characterization of the complexity class of functions that are computable in polynomial time
To explore theoretical aspects, we work with François Lamarche (Calligramme, LORIA and INRIA) on foundations and with Philippe Malbos (Institut Camille Jordan, Lyon) on homological tools
for polygraph analysis. On the practical side, we have started the development of Cat, an environment for certified polygraphic programming: as a first step, a compiler of polygraphic
programs in the
Tomlanguage is currently developped.
Mechanized deduction
deduction modulo
decision procedures
constrained theories
induction proofs
equational proofs
completion procedures
termination
On one hand, we have obtained new or refined results for proving properties of probabilistic, rule-based and functional programs, in particular termination, using both the inductive and
size-based approaches. We also began to develop a
Coqlibrary for certifying termination proofs.
On the other hand, we have further studied deduction modulo, identified an intrinsic complexity measure of a proof and a notion of “good proofs” in automated deduction, and explored the new
concept of superdeduction.
Rewriting and probabilities
Florent
Garnier
Claude
Kirchner
Florent Garnier has defended his PhD thesis "Terminaison en temps moyen fini de système de règles probabilistes", supervised by Claude Kirchner and Olivier Bournez (Carte team at LORIA),
in September 2007
Proving Properties of Reduction Relations
Hélène
Kirchner
In collaboration with Isabelle Gnaedig (Carte team at LORIA), we described in
Strong Normalization with Union and Existential Types
Colin
Riba
In
 -calculus plus rewriting in presence of implicit existential types. Usually, such proofs use interpretations of types by sets of strongly normalizing terms and rely on the soundess of
the interpretations: typable terms belongs to the interpretation of their types. Soundness requires types to be interpreted by sets of terms satisfying some closure conditions, while union
and implicit existential types are naturally interpreted by unions of type interpretations. However, in presence of rewriting, it is not trivial to find sound closure conditions that are
preserved by union. We have made two contributions to this question.
-calculus plus rewriting in presence of implicit existential types. Usually, such proofs use interpretations of types by sets of strongly normalizing terms and rely on the soundess of
the interpretations: typable terms belongs to the interpretation of their types. Soundness requires types to be interpreted by sets of terms satisfying some closure conditions, while union
and implicit existential types are naturally interpreted by unions of type interpretations. However, in presence of rewriting, it is not trivial to find sound closure conditions that are
preserved by union. We have made two contributions to this question.
First, we have given a necessary and sufficient condition for the closure condition of Girard's reducibility candidates to be stable by union
 -calculus as well as for the
-calculus as well as for the
 -calculus enriched with product, co-product and recursive types.
-calculus enriched with product, co-product and recursive types.
Second, in
Building Decision Procedures in the Calculus of Inductive Constructions
Frédéric
Blanqui
This work was done in collaboration with Jean-Pierre Jouannaud and Pierre-Yves Strub (LIX, Ecole Polytechnique).
It is commonly agreed that the success of future proof assistants will rely on their ability to incorporate computations within deductions in order to mimic the mathematician when
replacing the proof of a proposition P by the proof of an equivalent proposition P' obtained from P thanks to possibly complex calculations.
In
Our main result shows that this extension of the calculus of constructions does not compromise its main properties: confluence, strong normalization and decidability of proof-checking are
all preserved. We also showed in detail how a goal to be proved in the calculus of constructions is actually transformed into a goal in a decidable first-order theory. Based on this
transformation, we are currently developing a new version of Coq implementing this calculus, taking linear arithmetic and the theory of lists as targets combined via Shostak's algorithm.
Termination of higher-order rewrite systems
Frédéric
Blanqui
This work was done in collaboration with Jean-Pierre Jouannaud (LIX, Ecole Polytechnique) and Albert Rubio (Technical University of Catalonia).
In
In
Simple proofs in deduction modulo
Guillaume
Burel
Claude
Kirchner
Solving goals, like deciding word problems or resolving constraints, is much easier in some theory presentations than in others. We have designed a general proof-theoretic framework
centered around well-founded orderings of proofs and within which completion-like processes can be modeled around notions of saturation and redundancy
In
We also focused on the length of proofs in deduction modulo. Parikh proved a speed-up theorem stated by Gödel: proofs in second-order arithmetic can be unboundedly shorter than in first
order
Superdeduction
Horatiu
Cirstea
Paul
Brauner
Jonathan
Demange
Clément
Houtman
Claude
Kirchner
Following the seminal work of Benjamin Wack on extended natural deduction
The proof of strong normalization can be found in
Finally, we pointed out the benefits of superdeduction in the frame of interactive proof building by developing an implementation of superdeduction modulo using the
Tomlanguage. This prototype called
Lemuridæcan be downloaded from
Tom's CVS. The theoretical foundations of such a framework have been studied in
Inductive proof search
Claude
Kirchner
Hélène
Kirchner
Fabrice
Nahon
In the line of previous work on a proof theoretic framework to perform rewrite based inductive reasonning, Fabrice Nahon's PhD thesis
 and a set
and a set
Eof equalities
Whenever the equational rewrite system
 has good properties of termination, sufficient completeness, and whenever
has good properties of termination, sufficient completeness, and whenever
Eis constructor preserving, narrowing at defined-innermost positions is performed with unifiers which are constructor substitutions. This is especially interesting for associative and
associative-commutative theories for which the general proof search system is refined.
![]() -calculus and rewriting that we called rewriting calculus (
-calculus and rewriting that we called rewriting calculus (
![]() -calculus, for short)
. The notion of
-calculus, for short)
. The notion of
![]() -reduction of the rewriting calculus generalises
-reduction of the rewriting calculus generalises
![]() -reduction by considering matching on patterns which can be more elaborated than simple variables. We have been studying the expressiveness of this general formalism and the properties
of its various instances.
-reduction by considering matching on patterns which can be more elaborated than simple variables. We have been studying the expressiveness of this general formalism and the properties
of its various instances.![]() -calculus, and more generally in rewrite engines.
-calculus, and more generally in rewrite engines.