PDEs for Particles and Fluids
PDEs
Kinetic Equations
Conservation Laws
Hyperbolic Systems
Fluid Mechanics
Parabolic Systems
Computational Fluid Dynamics
Plasma Physics
Asymptotic analysis
The scientific activity of the project is concerned with PDEs arising from the physical description of particles and fluids. It covers various viewpoints:
 At first, the words “particles and fluids” could simply mean that we are interested independently in models for particles, which can either be considered as individuals (which leads to “
At first, the words “particles and fluids” could simply mean that we are interested independently in models for particles, which can either be considered as individuals (which leads to “
N-particle models”,
Nranging from 1 to many) or through a statistical description (which leads to kinetic equations) as well as in models for fluids like Euler and Navier-Stokes equations or plasma
physics.
 However, many particle systems can also be viewed as a fluid, via a passage from microscopic to macroscopic viewpoint, that is, a hydrodynamic limit.
However, many particle systems can also be viewed as a fluid, via a passage from microscopic to macroscopic viewpoint, that is, a hydrodynamic limit.
 Conversely, a fruitful idea to build numerical solvers for hyperbolic conservation laws consists in coming back to a kinetic formulation. This approach has recently motivated the
introduction of the so-called kinetic schemes.
Conversely, a fruitful idea to build numerical solvers for hyperbolic conservation laws consists in coming back to a kinetic formulation. This approach has recently motivated the
introduction of the so-called kinetic schemes.
 Eventually, one of the main topics of the project is to deal with models of particles interacting with a fluid.
Eventually, one of the main topics of the project is to deal with models of particles interacting with a fluid.
By nature these problems describe multiscale phenomena and one of the major difficulties when studying them lies in the interactions between the various scales: number of
particles, size, different time and length scales, coupling...
The originality of the project is to consider a wide spectrum of potential applications. In particular, the word “particles” covers various and very different physical
situations, like for instance:
- charged particles: description of semi-conductor devices or plasmas;
- photons, as arising in radiative transfer theory and astrophysics;
- neutrons, as arising in nuclear engineering;
- bacteria, individuals or genes as in models motivated by biology or population dynamics;
- planets or stars as in astrophysics;
- vehicles in traffic flow modelling;
- droplets and bubbles, as in Fluid/Particles Interaction models which arise in the description of sprays and aerosols, smoke and dust, combustion phenomena (aeronautics or
engine design), industrial process in metallurgy...
We aim at focusing on all the aspects of the problem:
 Modelling mathematically complex physics requires a deep discussion of the leading phenomena and the role of the physical parameters. With this respect, the asymptotic analysis is a
crucial issue, the goal being to derive reduced models which can be solved with a reduced numerical cost but still provide accurate results in the physical situations that are considered.
Modelling mathematically complex physics requires a deep discussion of the leading phenomena and the role of the physical parameters. With this respect, the asymptotic analysis is a
crucial issue, the goal being to derive reduced models which can be solved with a reduced numerical cost but still provide accurate results in the physical situations that are considered.
 The mathematical analysis of the equations provides important qualitative properties of the solutions: well-posedness, stability, smoothness of the solutions, large time behavior...
which in turn can motivate the design of numerical methods.
The mathematical analysis of the equations provides important qualitative properties of the solutions: well-posedness, stability, smoothness of the solutions, large time behavior...
which in turn can motivate the design of numerical methods.
 Eventually, we aim at developing specific numerical methods and performing numerical simulations for these models, in order to validate the theoretical results and shed some light on the
physics.
Eventually, we aim at developing specific numerical methods and performing numerical simulations for these models, in order to validate the theoretical results and shed some light on the
physics.
The team has been composed in order to study these various aspects simultaneously. In particular, we wish to keep a balance between modelling, analysis, development of
original codes and simulations.
Interactions of Micro- and Macroscopic Scales, Modelling and Simulations
Statistical Physics
Hydrodynamic Limit
Asymptotic Preserving Schemes
Radiative Transfer
Fluid-Particles Flows
Reduced Models; Hydrodynamic Limits
In the study of kinetic equations, it is a very usual strategy to perform a hydrodynamic limit, and then to get rid of the velocity variable and replace the kinetic equation by a
convection-diffusion model. This kind of derivation is well established, under various forms, and in several fields of applications: neutron transport, semiconductor theory, SHE models...
However, several questions of great interest have not yet been solved:
- The computation of the convection-diffusion coefficients of the limit equation, a question which leads to additional difficulties when the small mean free path
asymptotics are combined with a homogeneization limit. This problem is motivated by applications in nuclear engineering. In this case, the effective coefficients are defined through auxiliary
equations and suitable averages of the oscillatory coefficients.
- Some recent works have revealed the formation of singularities in the solutions of some limit convection-diffusion equations, while the original kinetic equation has
globally defined solutions. This is due to a coupling in the definition of the convective term with the macroscopic density. This singularity formation is typical of aggregation dynamics. It
occurs in models with gravitational forces in astrophysics, and chemotaxis models in biology. Therefore, the natural problems are either to provide a sharp analysis (theoretical and/or based
on numerics) of the singularity formation, or to complete the model to avoid such trouble.
- A crucial question for applications is to write models for intermediate regimes, for small but non zero values of the mean free path. Such models are required to remain
solvable with a moderate computational cost, and to preserve more features from the kinetic level (as for instance finite speeds of propagation, which is lost with a diffusion equation). An
example of such an intermediate model is the moment system obtained by using a closure by Entropy Minimization. We have proved recently that this model is indeed consistent with the diffusion
approximation, and we propose an original scheme to treat these equations numerically. We introduce a relaxation strategy which in turn is naturally amenable to the use of asymptotic
preserving splitting methods and anti-diffusive schemes for transport equations that are developed in the team. Therefore, we can compare various limited flux models and discuss on numerics
their properties and advantages.
Radiative Transfer Theory
We are interested in the equations of the radiative transfer theory which are motivated by the description of high temperature combustion processes (spacecraft propulsion, reentry
problems), space observation, nuclear weapons engineering, or inertial confinement fusion. Such problems can be described by a coupling between kinetic and macroscopic equations that comes
from the “collision term”, through energy, or energy-impulsion, exchanges. The hydrodynamic limit yields coupled macroscopic equations, with possibly two distinct temperatures: the
temperature of the radiations and the temperature of the material. Taking into account Doppler and relativistic effects adds convective terms, which in turn might give rise to the formation
of specific singularities.
The interesting points can be summarized as follows:
- The derivation of the reduced models, based on modeling arguments, is an issue, bearing in mind to describe a complete hierarchy of models;
- The coupling induces non trivial effects on the structure of the hydrodynamics system, which can modify strongly the qualitative properties of the solutions. In particular, the radiative
transfer equations might exhibit non standard shocks profiles, with possible discontinuities. The computation of such discontinuous shock profiles requires a very accurate and nondiffusive
numerical scheme for the convective terms. This also leads to the delicate question of the stability of travelling waves solutions.
These topics are the object of a very intense research activity e.g. at the Department of Computational Physics of the Los Alamos National Laboratory as well as at the
French Atomic Energy Agency (CEA). We develop alternative numerical methods, based on tricky splitting approaches. When dealing with kinetic models, such methods have to be specifically
designed to preserve the asymptotic properties of the model. In this approach, one computes on a time step the evolution of the unknown due the the convective terms, which will be handled by
antidiffusive schemes (see the paragraph Conservation Laws below), and on the next time step, we treat source and interaction terms, that can be nonlocal and/or stiff. This leads to a fully
explicit scheme which provides accurate results for a cheap numerical cost and which does not require a tedious inversion step as the implicit methods usually do. We are able to treat
numerically the full coupling of radiation with hydrodynamics (Euler equations) in the non equilibrium diffusion regime.
Fluid/Particles Interactions
These models arise in the modelling of disperse suspensions in fluids, say droplet or bubble motion. Their study is motivated by applications to combustion, rocket propulsor engineering,
biology, aerosols engineering, or for certain industrial processes... The main effect to take into account is the Stokes drag force, which is proportional to the relative velocity between the
particle and the surrounding fluid
F(
t,
x,
v) =
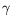 (
(
u(
t,
x)-
v). However, modelling remains a major issue in this field; in particular, here are some important questions :
- Complementary effects can be taken into account: the so-called Basset force, or the added mass effect, etc... For instance, when particles flow in a pipe, a phenomenological lift force,
proportional to
v×(
v-
u), has been proposed to mimic the tendency of particles to concentrate at the center of the pipe. Even though moderate in strength, such a force can have crucial
effects on blood flows, or on industrial processes of steel production.
- Up to now, there are only a few contributions on the description of size variations, by coagulation or fragmentation and break-up. However, in practical situations, as for combustion or
biology applications, these phenomena cannot be neglected.
- Of course, the coupling with the evolution of the surrounding fluid is a crucial question that leads naturally to problems of asymptotics. Effects of “turbulence”, which roughly means
high and fast variations of
uon the behavior of the particles, have been analyzed in some simplified situations.
The coupling with the Navier-Stokes or the Euler equations is a privileged subject for SIMPAF. Some asymptotics lead to two-phase flows models, that we are interested in investigating both
from a theoretical and numerical point of view. In particular, the effect of an external force (gravitational or centrifugal) can lead to sedimentation profiles that are suspected to be
stable; we would like to confirm these heuristics by a thorough numerical and theoretical study. Of course, such investigations require efficient numerical schemes to solve the fluid
equations with source terms, which will be detailed in the next sections. To this end, we adapt to this framework the numerical schemes we develop for radiative transfer problems, based on
splitting methods and a suitable use of the asymptotic expansion.
Charged Particles
Plasma Physics
Ohm's law
Vlasov-Poisson equations
Vlasov-Maxwell equations
Euler-Poisson equations
Euler-Maxwell equations
Magnetized plasmas
Spacecraft charge modeling
Modeling of Plasma Confinement
Plasmas, the fourth state of the matter, play an important role in many branches of physics, such as thermonuclear fusion research, astrophysics and space physics. A plasma is a
(partially) ionized gas where charged particles interact via electromagnetic fields. Since the announcement of the creation of the experimental fusion reactor ITER, and with the progress on
the FIC program, plasmas and their modelling got a renewed interest.
The nuclear fusion mechanisms result from the strong confinement of charged particles, either by inertial confinement (nuclear fusion reactions are initiated by heating and compressing a
target - a pellet that most often contains deuterium and tritium - by the use of intense laser or ion beams) or by the - more promising - magnetic fusion confinement. The tokamaks are
experimental devices which produce a toroidal magnetic field for confining a plasma.
The description of these phenomena is extremely complex and leads to delicate problems in mathematical analysis and numerical simulation. Actually, plasmas may be described with various
levels of detail. The simplest possibility is to treat the plasma as a single fluid governed by the Navier Stokes Equations. A more general description is the two-fluid picture, where the
ions and electrons are considered to be distinct. If electric or magnetic fields are present, then the Maxwell equations will be needed to describe them. The coupling of the description of a
conductive fluid to electromagnetic fields is known generally as magnetohydrodynamics, or simply MHD.
For some cases the fluid description is not sufficient. Then, the kinetic models may become useful. Kinetic models include information on distortions of the velocity distribution functions
with respect to a Maxwell-Boltzmann distribution. This may be important when currents flow, when waves are involved, or when gradients are very steep.
The main mathematical difficulties are therefore linked to the conjunction of the following elements
these two types of models are strongly nonlinear,
the unknowns depend on the time and space variables and, in the case of kinetic models, also on the velocity variables. Therefore, we can be led to work with variables
of 1 + 3 + 3 dimensions,
there exist many very different scales (time scale, characteristic length ...)
The numerical resolution of a complete system of equations, with meshes adapted to the lower scales, leads to prohibitive computational costs both in terms of memory and time. The
derivation of new reduced models, corresponding to relevant asymptotic regimes (high magnetic field for example), is therefore a crucial issue. Moreover, very serious efforts must be done on
the numerical methods that are used in order to reproduce the typical phenomena. This work depends on the one hand on seriously thinking over the models, the physical parameters, their
typical respective scales, and on the other hand over some arguments of asymptotic analysis, which can particularly call on deterministic or random homogeneization.
Spacecraft Environment
Satellites in geostationary and low Earth orbits naturally evolve in a plasma. This ionized environment induces some perturbations which may lead to many kind of faults and to the partial
or complete loss of a mission. The satellites are covered by dielectric coatings in order to protect them against thermal radiations. Electrons and ions species of the space plasma interact
with the external surfaces of the satellite and modify their electrostatic charges. This effect produces potential differences between the satellite surfaces and its electric mass. When the
electric field exceeds a certain level, an electrostatic discharge appears. This electric current pulse is able to disrupt the equipments, to damage the external surfaces and even to destroy
some electronic components. The plasma may also be created by an other source : the electric thrusters. This new propulsion device uses the electric energy supplied by solar arrays to speed
up charged species. It is more and more used in satellite industry and has preference over the classical chemical propulsion. Indeed, this last needs a very large amount of propellant
inducing an expensive rocket launch. On the one hand, the electric thrusters allow to significantly reduce the satellite weight. On the other hand, it is necessary to understand their
potential impacts on the other systems of the satellite.
This line of research, which continues former works of the team CAIMAN at Sophia Antipolis, is the object of a strong collaboration with the Department Research and Technology of the
company Thales and the PhD of S. Borghol is essentially devoted to this subject.
Effective Energy Dissipation Models for Charged Particles
In models of charge transport, say transport of electrons, a phenomenological friction force is generally introduced, which is proportional to the velocity
v. Our idea is to go back to a more microscopic framework, with a description of the energy exchanges between the electrons and the surrounding medium. In turn, the dissipation of
energy by the medium will lead to an effective friction force. The first contributions only model the transport of a unique particle, and we aim at considering now a plasma, through a
statistical description. This yields a Vlasov-Poisson-like model. (More precisely, the kinetic equation is coupled to a finite, or infinite, set of oscillators.) This program requires efforts
in modelling and analysis, but the questions are also really challenging for numerics, due, on the one hand, to the large number of degrees of freedom involved in the equation, and on the
other hand, to the presence of stiff terms. In this way, we expect to be able to shed light on the range of validity of the Ohm law. Similar considerations also apply for heat transport, and
the derivation of the Fourier law.
Simulations of Complex Fluid Flows
Conservation Laws
Anti-Diffusive Schemes
Viscous Flows
Control
Turbulence
Finite elements methods
Finite volume methods
Conservation Laws
A major issue in the numerical analysis of systems of conservation laws is the preservation of singularities (shocks, contact discontinuities...). Indeed, the derivatives of the solutions
usually blow-up in finite time. The numerical scheme should be able to reproduce this phenomenon with accuracy, i.e. with a minimum number of points, by capturing the profile of the
singularity (discontinuity), and by propagating it with the correct velocity. The scheme should also be able to give some insight on the interactions between the possible singularities. Quite
recently, new anti-diffusive strategies have been introduced, and successfully used on fluid mechanics problems. We focus on multidimensional situations, as well as on boundary value
problems. Since a complete theory is not yet available, the numerical analysis of some prototype systems of conservation laws is a good starting point to understand multi-dimensional
problems. In particular, a good understanding of the linear case is necessary. This is not achieved yet on the numerical point of view on general meshes. This question is particularly
relevant in industrial codes, where one has to solve coupled systems of PDEs involving a complex coupling of different numerical methods, which implies we will have to deal with unstructured
meshes. Thus, deriving non-dissipative numerical schemes for transport equations on general meshes is an important issue. Furthermore, transport phenomena are the major reason why a numerical
diffusion appears in the simulation of non-linear hyperbolic conservation laws and contact discontinuities are more subject to this than shocks because of the compressivity of shock waves
(this is another reason why we focus at first on linear models).
The next step is to combine non-dissipation with non-linear stability. An example of such a combination of preservation of sharp shocks and entropy inequalities has been
recently proposed for scalar equations and is still at study. It has also been partially done in dimension one for Euler equations.
Of course, there are plenty of applications for the development of such explicit methods for conservation laws. We are particularly interested in simulation of macroscopic
models of radiative hydrodynamics, as mentioned above. Another field of application is concerned with polyphasic flows and it is worth specifying that certain numerical methods designed by F.
Lagoutière are already used in codes at the CEA for that purpose. We also wish to apply these methods for coagulation-fragmentation problems and for PDEs modelling the growth of tumoral
cells; concerning these applications, the capture of the large time state is a particularly important question.
Control in Fluid Mechanics
Nowadays, passive control techniques are widely used to improve the performances of planes or vehicles. In particular these devices can sensibly reduce energy consumption or noise
disturbances. However, new improvements can be obtained through an active control of the flow, which means by activating mechanical devices. This is a very promising theme.
The first results are concerned with the control of the 2D compressible Navier-Stokes equations over a dihedral plane. The technical device consists in a small hole which allows to suck or
to inject some fluid in the flow, depending on the pressure measured at another point. This improves the aerodynamics performance of the dihedral. Variants are possible, for instance by
considering several such devices and taking into account the local properties of the flow.
Another work is concerned with simulation of the control of low Reynolds number flows (laminar regimes) over a backward facing step by imposing pulsed inlet velocities. Such a flow can be
considered as a toy-model for the modelling of combustion phenomena. The goal is to understand and control vortex formations, by making the frequency and amplitude of the incoming fluid
vary.
Recently, previous results on the step were generalized to the transitional regime, with a work of E. Creusé, A. Giovannini (IMFT Toulouse) and I. Mortazavi (EPI Inria MC2, Bordeaux). The
nonstationarity property of the uncontrolled flow allows to use some closed-loop control strategies. The control process is either a global one, by imposing a pulsed inlet velocity like for
the laminar case, or a local one by the use of two horizontal jets located on the vertical side of the step.
Our current objective is now to apply such techniques on the "Ahmed body geometry", which can be considered as a first approximation of a vehicle profile. This work is performed in
collaboration between E. Creusé and C.H. Bruneau (EPI Inria MC2, Bordeaux) in the context of the research and innovation program on terrestrial transports supported by the ANR and the ADEME,
leaded by Renault and PSA and managed by Jean-Luc Aider (ESPCI Paris). One of the main points is now to understand and to make use of the correlation law between the actions imposed on the
wall and the drag coefficient of the profile. Significant energy saving could then be obtained.
Numerical Methods for Viscous Flows
In the large scale computations of fluid flows, several different numerical quantities appear that are associated to different eddies, structures or scales (in space as well as in time).
An important challenge in the modelling of turbulence and of the energy transfer for dissipative equations (such as Navier-Stokes equations, reaction-diffusion equations) is to describe or to
model, for the long time behavior, the interaction between large and small scales. They are associated to slow and fast wavelengths respectively. The multiscale method consists in modelling
this interaction on numerical grounds for dissipative evolution equations. In Finite Elements and Finite Differences discretizations the scales do not appear naturally as in spectral
approximations, their construction is obtained by using a recursive change of variables operating on nested grids; the nodal unknowns (Y) of the coarse grids are unchanged (they are of the
order of magnitude of the physical solution) and those of the fine grids are replaced by proper error interpolation, namely the incremental unknowns (Z); the magnitude of the Zs is then
"small". This allows to make a separation of the eddies in space (presence of nodal and incremental quantities) but also in frequency since the incremental unknowns are supported by the fine
grids which capture the high frequencies while the nodal unknowns are defined on coarse grids which can represent only slow modes. Note that this approach differs from the LES model that
proposes to split the flow into a mean and a fluctuation component, this last one having small moments but not necessarily a small magnitude. This change of variable defines also a
hierarchical preconditioner. It is well known that the (semi)explicit time marching schemes have their stability region limited by the high modes, so a way to enhance the stability is to
tread numerically the scales (Y and Z) in a different manner. The inconsistency carried by the new scheme acts only on small quantities allowing for efficient and accurate schemes for the
long time integration of the equations. We develop and apply this approach to the numerical simulation of Navier-Stokes equations in highly non stationary regimes. In this framework of
numerical methods, we focus on the domain decomposition method together with multiscale method for solving incompressible bidimensional NSE; the stabilized explicit time marching schemes are
also studied.
The already written code can be used to treat certain low Mach number models arising in combustion theory, as well as models describing mixing of compressible fluids arising for instance
when describing the transport of pollutants. The interesting thing is that this kind of model can be derived by a completely different approach through a kinetic model. Besides, this model
presents interesting features, since it is not clear at all whether solutions can be globally defined without smallness assumptions on the data. Then, a numerical investigation is very useful
to check what the actual behavior of the system is. Accordingly, our program is two-fold. On the one hand, we will develop a density dependent Navier-Stokes code, in 2D, the incompressibility
condition being replaced by a non standard condition on the velocity field. The numerical strategy we use mixes a Finite Element method for computing the velocity field to a Finite Volume
approach to evaluate the density. As a by-product, the code should be able to compute a solution of the 2D incompressible Navier-Stokes system, with variable density. On the other hand, we
wish to extend our kinetic asymptotic-based schemes to such problems.
![]() Studying models that describe the evolution of a fluid and/or of a large number of particles;
Studying models that describe the evolution of a fluid and/or of a large number of particles;![]() Discussing the relevance and the range of validity of these models;
Discussing the relevance and the range of validity of these models;![]() Analyzing connections between different levels of modelling;
Analyzing connections between different levels of modelling;![]() Developing efficient numerical methods to compute the solutions of such models.
Developing efficient numerical methods to compute the solutions of such models.