Effective 3D global visibility, theory and applications
Julien
Demouth
Hazel
Everett
Marc
Glisse
Xavier
Goaoc
Sylvain
Lazard
Sylvain
Petitjean
Linqiao
Zhang
Shadows play a central role in human perception and a wide variety of approaches have been considered for simulating and rendering them. Unfortunately, computing realistic shadows
efficiently is a very difficult problem, particularly in the case of non-point light sources, due to the complicated internal structure that such shadows may have. We presented some surprising
combinatorial results on the umbra and penumbra cast by non-trivial light sources. A point is in the umbra if it does not see any part of any light source; it is in full light if it sees
entirely all the light sources; otherwise, it is in the penumbra. For instance, we proved that a segment light source may cast on a plane, in the presence of two fat polytopes of size
n, up to
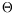 (
(
n)connected components of umbra in the worst case. We also presented several lower and upper bounds in the case of segment and polygonal light sources in a scene
composed of polytopes. These results are the first non-trivial bounds on the size of the umbra and show that the umbra can be surprisingly complicated, even in the presence of disjoint fat
obstacles. They were presented at the 2007 SoCG conference
Lines tangent to and intersecting geometric objects play a fundamental role in visibility problems, for instance, as generators of shadow boundaries. Although line geometry is a classical
subject, many gaps remain. In particular, little is known on how the geometry of the objects determine the structure of their line transversals. We proved that the set of directions of line
transversals to disjoint balls in
 in a given order is a convex subset of the space of directions. This has a number of applications in line geometry, for example tight combinatorial bounds and Helly-type theorems. These
results have been presented at the 2007 SoCG conference
in a given order is a convex subset of the space of directions. This has a number of applications in line geometry, for example tight combinatorial bounds and Helly-type theorems. These
results have been presented at the 2007 SoCG conference
We studied over the last years the complexity of the set of lines and free line segments tangent to possibly intersecting arbitrary convex polytopes and presented an efficient sweep-plane
algorithm for computing such lines or free segments. These results, which significantly improve the state of the art on this subject, were published this year in the journal
SIAM Journal on Computing
We also published this year some results on tangents to triangles in the journal
Discrete and Computational Geometry
nthat approximates a surface in some reasonable way has silhouettes of expected size
 , where the average is taken over all points of view
, where the average is taken over all points of view
Finally, Marc Glisse defended his Ph.D. on the combinatorics of line and segments in 3D visibility
Exact geometric computing for low-degree surfaces
Jinsan
Cheng
Laurent
Dupont
Hazel
Everett
Sylvain
Lazard
Luis
Penaranda
Maria
Pentcheva
Sylvain
Petitjean
Marc
Pouget
Elias
Tsigaridas
We developed, over the last years, the first efficient algorithm for computing an exact parameterization of the intersection of two quadric surfaces (ellipsoids, paraboloids, hyperboloids,
etc.) in three-dimensional real space given by implicit equations with rational coefficients. We also produced a C++ implementation of this algorithm which is the only existing solution for
computing exactly a parameterization of the intersection of two quadrics. A series of three articles describing the theoretical contributions of this work was accepted for publication in 2007
in the
Journal of Symbolic Computation
We have recently started working on the problem of computing the medial axis or Voronoi diagram of polyhedra in 3D. These structures are largely used in applications; the medial axis is, for
instance, a way of representing a shape by its topological skeleton. Such a diagram is a partition of space into cells, each of which consists of the points closest to one particular object
than to any other. Moreover, the set of points equidistant to two lines (or to a line and a point) is a quadric and the set of points equidistant to three lines is the intersection of two
quadrics. While such structures are well-understood in the plane and for simple situations in higher dimensions (e.g. for sets of points), a lot remains to be done; for example, there is no
working solution for computing exactly the medial axis of a polyhedron. We started by considering the Voronoi diagram of lines and we presented some very nice results characterizing the
topology of the Voronoi diagrams of three lines. We proved, in particular, that the topology is invariant for lines in general position and we obtained a monotonicity property on the arcs of
the diagram. We deduced a simple algorithm for sorting points along such an arc, which is presumably of great interest for future efficient algorithms for computing the medial axis of a
polyhedron. The proof technique, which relies heavily upon modern tools of computer algebra, is also of great interest in its own right. These results were presented in the 2007 SoCG
conference
We have presented a complete, exact and efficient algorithm and its implementation for computing the adjacency graph of an arrangement of integer quadrics
Since our work on quadrics can not easily be extended to more complex primitives (cubics, quartics, ...), an orthogonal research direction is to consider the (certified) approximation of
complex shapes by lower-degree objects, with the idea that a simple, intermediate representation has great potential for dealing with curved objects. We have worked in this direction by
studying the approximation of smooth curves by tangent continuous conic splines
We also started working on the problem of geometric computing with algebraic tools. Our goal is two-fold. First, we want to make state-of-the-art algebraic software more accessible to the
computational geometry community, in particular, through the computational geometric library CGAL. Second, our goal is to demonstrate to which extent such state-of-the-art certified algebraic
root-finding systems can be used in geometric algorithms to obtain certified constructions involving curved objects without hindering performance. For that purpose, we focus on the problem of
computing arrangements of algebraic curves in two dimensions. We already have some results in these two directions. In particular, we have presented a preliminary version of a univariate
algebraic kernel for CGAL at the
International Workshop on Robust Shape Operations Organizedin Sophia-Antipolis in September 2007.
On the thematic of geometric computing for low-degree surfaces, Sylvain Petitjean and Sylvain Lazard defended their Habilitation
Finally, it should be noted that we also addressed other problems in computational geometry. We obtained, in particular, results on furthest polygon Voronoi
diagrams
![]() where a prototype of a 3D computer model is constructed by first decomposing the model into layers and then manufacturing separately each layer, typically out of wood of standard
thickness (e.g. 1 cm), with a three-axis CNC (Computer Numerical Controls) milling machine. The layers are then assembled together to form the object. The Stratoconception
where a prototype of a 3D computer model is constructed by first decomposing the model into layers and then manufacturing separately each layer, typically out of wood of standard
thickness (e.g. 1 cm), with a three-axis CNC (Computer Numerical Controls) milling machine. The layers are then assembled together to form the object. The Stratoconception
![]() technique is cheap and allows fast prototyping of large models.
technique is cheap and allows fast prototyping of large models.