Overall Objectives
Overall Objectives
hidden Markov model (HMM)
particle filtering
risk evaluation
localisation
navigation and tracking
rare event simulation
The scientific objectives of ASPI are the design, analysis and implementation of interacting Monte Carlo methods, also known as particle methods, with focus on
statistical inference in hidden Markov models, e.g. state or parameter estimation, including particle filtering,
risk evaluation, including simulation of rare events.
The whole problematic is multidisciplinary, not only because of the many scientific and engineering areas in which particle methods are used, but also because of the diversity of the
scientific communities which have already contributed to establish the foundations of the field
target tracking, interacting particle systems, empirical processes, genetic algorithms (GA), hidden Markov models and nonlinear filtering, Bayesian statistics, Markov chain
Monte Carlo (MCMC) methods, etc.
Intuitively speaking, interacting Monte Carlo methods are sequential simulation methods, in which particles
explorethe state space by mimicking the evolution of an underlying random process,
learnthe environment by evaluating a fitness function,
and
interactso that only the most successful particles (in view of the value of the fitness function) are allowed to survive and to get offsprings at the next generation.
The effect of this mutation / selection mechanism is to automatically concentrate particles (i.e. the available computing power) in regions of interest of the state space. In the
special case of particle filtering, which has numerous applications under the generic heading of positioning, navigation and tracking, in
target tracking, computer vision, mobile robotics, ubiquitous computing and ambient intelligence, sensor networks, etc.,
each particle represents a possible hidden state, and is multiplied or terminated at the next generation on the basis of its consistency with the current observation, as quantified by the
likelihood function. These genetic–type algorithms are particularly adapted to situations which combine a prior model of the mobile displacement, sensor-based measurements, and a base of
reference measurements, for example in the form of a digital map (digital elevation map, attenuation map, etc.). In the most general case, particle methods provide approximations of probability
distributions associated with a Feynman–Kac flow, by means of the weighted empirical probability distribution associated with an interacting particle system, with applications that go far
beyond filtering, in
simulation of rare events, simulation of conditioned or constrained random variables, interacting MCMC methods, molecular simulation, etc.
ASPI essentially carries methodological research activities, rather than activities oriented towards a single application area, with the objective of obtaining generic results with high
potential for applications, and of implementing up–to–date results on a few appropriate examples, through collaboration with industrial partners.
The main applications currently considered are geolocalisation and tracking of mobile terminals, terrain–aided navigation, data fusion for indoor localisation, risk assessment for complex
hybrid systems, e.g. in air traffic management, and protection of digital documents.
Scientific Foundations
Monte Carlo methods
Monte Carlo methods are numerical methods that are widely used in situations where (i) a stochastic (usually Markovian) model is given for some underlying process, and (ii) some
quantity of interest should be evaluated, that can be expressed in terms of the expected value of a functional of the process trajectory, which includes as an important special case the
probability that a given event has occurred. Numerous examples can be found, e.g. in financial engineering (pricing of options and derivative securities)
Nof the sample goes to infinity, with rate
 and the asymptotic variance can be estimated using an appropriate central limit theorem. To reduce the variance of the estimator, many variance reduction techniques have been proposed.
Still, running independent Monte Carlo simulations can lead to very poor results, because trajectories are generated
blindly, and only afterwards are the corresponding weights evaluated. Some of the weights can happen to be negligible, in which case the corresponding trajectories are not going to
contribute to the estimator, i.e. computing power has been wasted.
and the asymptotic variance can be estimated using an appropriate central limit theorem. To reduce the variance of the estimator, many variance reduction techniques have been proposed.
Still, running independent Monte Carlo simulations can lead to very poor results, because trajectories are generated
blindly, and only afterwards are the corresponding weights evaluated. Some of the weights can happen to be negligible, in which case the corresponding trajectories are not going to
contribute to the estimator, i.e. computing power has been wasted.
A recent and major breakthrough, a brief mathematical presentation of which is given in
explorethe state space under the effect of a
mutationmechanism which mimics the evolution of the underlying process,
and are
replicatedor
terminated, under the effect of a
selectionmechanism which automatically concentrates the particles, i.e. the available computing power, into regions of interest of the state space.
In full generality, the underlying process is a discrete–time Markov chain, whose state space can be
finite, continuous, hybrid (continuous / discrete), graphical, constrained, time varying, pathwise, etc.,
the only condition being that it can easily be
simulated. The very important case of a sampled continuous–time Markov process, e.g. the solution of a stochastic differential equation driven by a Wiener process or a more general Lévy
process, is also covered.
In the special case of particle filtering, originally developed within the tracking community, the algorithms yield a numerical approximation of the optimal filter, i.e. of the conditional
probability distribution of the hidden state given the past observations, as a (possibly weighted) empirical probability distribution of the system of particles. In its simplest version,
introduced in several different scientific communities under the name of
bootstrap filter
Particle methods are currently being used in many scientific and engineering areas
positioning, navigation, and tracking
Other examples of the many applications of particle filtering can be found in the contributed volume
Particle methods are very easy to implement, since it is sufficient in principle to simulate independent trajectories of the underlying process. The whole problematic is multidisciplinary,
not only because of the already mentioned diversity of the scientific and engineering areas in which particle methods are used, but also because of the diversity of the scientific communities
which have contributed to establish the foundations of the field
target tracking, interacting particle systems, empirical processes, genetic algorithms (GA), hidden Markov models and nonlinear filtering, Bayesian statistics, Markov chain
Monte Carlo (MCMC) methods.
Particle approximations of Feynman–Kac distributions
The following abstract point of view, developed and extensively studied by Pierre Del Moral
are selected according to their respective weights (selection step),
move according to the Markov transition kernel (mutation step),
are weighted by evaluating the fitness function (weighting step).
The algorithm yields a numerical approximation of the Feynman–Kac distribution as the weighted empirical probability distribution associated with a system of particles, and many asymptotic
results have been proved as the number
Nof particles (sample size) goes to infinity, using techniques coming from applied probability (interacting particle systems, empirical processes
convergence in
Lp, convergence as empirical processes indexed by classes of functions, uniform convergence in time, see also
Beyond the simplest
bootstrapversion of the algorithm, many algorithmic variations have been proposed
are selected according to their respective weights (selection step),
move according to the proposed importance Markov transition kernel (mutation step),
are weighted by evaluating the corresponding importance function, which now depends on the Markov transition (weighting step).
Many of the early convergence results proved in the literature assume that particles are redistributed (i) using sampling with replacement and (ii) at each time step, and move
according to the original Markov transition kernel. Systematically studying the impact of the proposed algorithmic variants on the convergence results is still the subject of active
research.
Statistics of HMM
hidden Markov model (HMM)
asymptotic statistics
local asymptotic normality (LAN)
exponential forgetting
exponential stability
Hidden Markov models (HMM) form a special case of partially observed stochastic dynamical systems, in which the state of a Markov process (in discrete or continuous time, with finite or
continuous state space) should be estimated from noisy observations. The conditional probability distribution of the hidden state given past observations is a well–known example of a normalized
(nonlinear) Feynman–Kac distribution, see
Beyond the recursive estimation of a hidden state from noisy observations, the problem arises of statistical inference of HMM with general state space
Large time asymptotics A fruitful approach is the asymptotic study, when the observation time increases to infinity, of an extended Markov chain, whose state includes
(i) the hidden state, (ii) the observation, (iii) the prediction filter (i.e. the conditional probability distribution of the hidden state given observations at all previous time
instants), and possibly (iv) the derivative of the prediction filter with respect to the parameter. Indeed, it is easy to express the log–likelihood function, the conditional least–squares
criterion, and many other clasical contrast processes, as well as their derivatives with respect to the parameter, as additive functionals of the extended Markov chain.
The following general approach has been proposed
first, prove an exponential stability property (i.e. an exponential forgetting property of the initial condition) of the prediction filter and its derivative, for a
misspecified model,
from this, deduce a geometric ergodicity property and the existence of a unique invariant probability distribution for the extended Markov chain, hence a law of large
numbers and a central limit theorem for a large class of contrast processes and their derivatives, and a local asymptotic normality property,
finally, obtain the consistency (i.e. the convergence to the set of minima of the associated contrast function), and the asymptotic normality of a large class of minimum
contrast estimators.
This programme has been completed in the case of a finite state space
Small noise asymptotics Another asymptotic approach can also be used, where it is rather easy to obtain interesting explicit results, in terms close to the language of
nonlinear deterministic control theory
The following results have been obtained using this approach
the consistency of the maximum likelihood estimator (i.e. the convergence to the set
Mof global minima of the Kullback–Leibler divergence), has been obtained using large deviations techniques, with an analytical approach
if the abovementioned set
Mdoes not reduce to the true parameter value, i.e. if the model is not identifiable, it is still possible to describe precisely the asymptotic behavior of the estimators
rof the Fisher information matrix
Iis constant in a neighborhood of the set
M, then this set is a differentiable submanifold of codimension
r, (ii) the posterior probability distribution of the parameter converges to a random probability distribution in the limit, supported by the manifold
M, absolutely continuous w.r.t. the Lebesgue measure on
M, with an explicit expression for the density, and (iii) the posterior probability distribution of the suitably normalized difference between the parameter and its projection on
the manifold
M, converges to a mixture of Gaussian probability distributions on the normal spaces to the manifold
M, which generalized the usual asymptotic normality property,
it has been shown
I, in terms of the Kalman filter associated with the linear tangent linear Gaussian model, and (ii) the score function (i.e. the derivative of the log–likelihood function w.r.t.
the parameter), evaluated at the true value of the parameter and suitably normalized, converges to a Gaussian r.v. with zero mean and covariance matrix
I.
Multilevel splitting for rare event simulation
rare event simulation
risk evaluation
reliability
multilevel splitting
branching
population extinction
asymptotic variance
See
The estimation of the small probability of a rare but critical event, is a crucial issue in industrial areas such as
nuclear power plants, food industry, telecommunication networks, finance and insurance industry, air traffic management, etc.
In such complex systems, analytical methods cannot be used, and naive Monte Carlo methods are clearly unefficient to estimate accurately very small probabilities. Besides importance
sampling, an alternate widespread technique consists in multilevel splitting
Propagation of uncertainty Multilevel splitting can be used in static situations. Here, the objective is to learn the probability distribution of an output random
variable
Y=
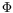 (
(
X), where the function
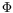 is only defined pointwise for instance by a computer programme, and where the probability distribution of the input random variable
is only defined pointwise for instance by a computer programme, and where the probability distribution of the input random variable
Xis known and easy to simulate from. More specifically, the objective could be to compute the probability of the output random variable exceeding a threshold, or more generally to
evaluate the cumulative distribution function of the output random variable for different output values. This problem is characterized by the lack of an analytical expression for the function,
the computational cost of a single pointwise evaluation of the function, which means that the number of calls to the function should be limited as much as possible, and finally the complexity
and/or unavailability of the source code of the computer programme, which makes any modification very difficult or even impossible, for instance to change the model as in importance sampling
methods.
The key issue is to learn as fast as possible regions of the input space which contribute most to the computation of the target quantity. The proposed splitting methos consists in
(i) introducing a sequence of intermediate regions in the input space, implicitly defined by exceeding an increasing sequence of thresholds or levels, (ii) counting the fraction of
samples that reach a level given that the previous level has been reached already, and (iii) regenerating the sample at each intermediate step, through redistribution. In this way, the
algorithm learns
the transition probability between successive levels, hence the probability of reaching each intermediate level,
and the probability distribution of the input random variable, conditionned on the output variable reaching each intermediate level.
A further remark, is that this conditional probability distribution is precisely the optimal (zero variance) importance distribution needed to compute the probability of reaching the
considered intermediate level.
Rare event simulation To be specific, consider a complex dynamical system modelled as a Markov process, whose state can possibly contain continuous components and finite
components (mode, regime, etc.), and the objective is to compute the probability, hopefully very small, that a critical region of the state space is reached by the Markov process before a final
time
T, which can be deterministic and fixed, or random (for instance the time of return to a recurrent set, corresponding to a nominal behaviour).
The proposed splitting method consists in (i) introducing a decreasing sequence of intermediate, more and more critical, regions in the state space, (ii) counting the fraction of
trajectories that reach an intermediate region before time
T, given that the previous intermediate region has been reached before time
T, and (iii) regenerating the population at each stage, through redistribution. In addition to the non–intrusive behaviour of the method, the splitting methods make it possible to
learn the probability distribution of typical critical trajectories, which reach the critical region before final time
T, an important feature that methods based on importance sampling usually miss. Many variants have been proposed, whether
the branching rate (number of offsprings allocated to a successful trajectory) is fixed, which allows for depth–first exploration of the branching tree, but raises the
issue of controlling the population size,
the population size is fixed, which requires a breadth–first exploration of the branching tree, with random (multinomial) or deterministic allocation of offsprings,
etc.
Just as in the static case, the algorithm learns
the transition probability between successive levels, hence the probability of reaching each intermediate level,
and the entrance probability distribution of the Markov process in each intermediate region.
Contributions have been given to
minimizing the asymptotic variance, obtained through a central limit theorem, with respect to the shape of the intermediate regions (selection of the importance
function), to the thresholds (levels), to the population size, etc.
controlling the probability of extinction (when not even one trajectory reaches the next intermediate level),
designing and studying variants suited for hybrid state space (resampling per mode, marginalization),
and in the static case, to
minimizing the asymptotic variance, obtained through a central limit theorem, with respect to intermediate levels, to the Metropolis kernel introduced in the mutation
step, etc.
Application Domains
Localisation, navigation and tracking
localisation
navigation
tracking
See
Among the many application domains of particle methods, or interacting Monte Carlo methods, ASPI has decided to focus on applications in localisation (or positioning), navigation and
tracking
a prior dynamical model of typical evolutions of the mobile, such as inertial estimates and prior model for inertial errors,
measurements provided by sensors,
and possibly a digital map providing some useful feature (terrain altitude, power attenuation, etc.) at each possible position.
In some applications, another useful source of information is provided by
a map of constrained admissible displacements, for instance in the form of an indoor building map,
which particle methods can easily handle (map-matching). This Bayesian dynamical estimation problem is also called filtering, and its numerical implementation using particle methods, known
as particle filtering, has been introduced by the target tracking community
target tracking, integrated navigation, points and / or objects tracking in video sequences, mobile robotics, wireless communications, ubiquitous computing and ambient
intelligence, sensor networks, etc.
ASPI is contributing to several applications of particle filtering in positioning, navigation and tracking, such as geolocalisation and tracking in wireless communications, terrain–aided
navigation, see
Rare event simulation
rare event simulation
risk evaluation
reliability
See
Another application domain of particle methods, or interacting Monte Carlo methods, that ASPI has decided to focus on is the estimation of the small probability of a rare but critical event,
in complex dynamical systems. This is a crucial issue in industrial areas such as
nuclear power plants, food industry, telecommunication networks, finance and insurance industry, air traffic management, etc.
In such complex systems, analytical methods cannot be used, and naive Monte Carlo methods are clearly unefficient to estimate accurately very small probabilities. Besides importance
sampling, an alternate widespread technique consists in multilevel splitting
ASPI is contributing to several applications of multilevel splitting for rare event simulation, such as risk assessment in air traffic management, see
New Results
Particle methods with adaptive resampling
François
Le Gland
adaptive sampling
effective sample size
This is a collaboration with Élise Arnaud, from université Joseph Fourier and INRIA Grenoble — Rhône Alpes.
A longstanding problem in particle or sequential Monte Carlo (SMC) methods is to mathematically prove the popular belief that resampling does improve the performance of the estimation (this
of course is not always true, and the real question is to clarify classes of problems where resampling helps). A more pragmatic answer to the problem is to use adaptive procedures that have
been proposed on the basis of heuristic considerations, where resampling is performed only when it is felt necessary, i.e. when some criterion (effective number of particles, entropy of the
sample, etc.) reaches some prescribed threshold. It still remains to mathematically prove the efficiency of such adaptive procedures. Our first contribution has been to consider a design where
resampling is performed at some intermediate fixed time instants, and to optimize the asymptotic variance of the estimation error w.r.t. the resampling time instants. The second contribution
has been to prove a central limit theorem for particle methods with adaptive resampling, using an interpretation of particle methods where importance weights are interpreted as particles
Non asymptotic variance estimates for unnormalized Feynman–Kac particle models
Frédéric
Cérou
Pierre
Del Moral
Arnaud
Guyader
interacting particle systems
Feynman–Kac semigroups
nonasymptotic estimates
genetic algorithms
Boltzmann–Gibbs measures
Monte Carlo models
rare events
We have obtained
L2-relative error of these weighted particle measures grows linearly with respect to the time horizon yielding what seems to be the first results of this type for this class of
unnormalized models. We have also illustrated these results in the context of particle simulation of static Boltzmann–Gibbs measures and restricted distributions, with a special interest in
rare event analysis. For rare events, these results yield to asymptotic efficiency when used in conjunction with a good importance function.
Sequential data assimilation: ensemble Kalman filter vs. particle filter
François
Le Gland
Vu Duc
Tran
data assimilation
ensemble Kalman filter (EnKF)
mean–field interaction
This is a collaboration with Valérie Monbet, from université de Bretagne Sud.
Surprisingly, very little was known about the asymptotic behaviour of the ensemble Kalman filter
 , as the number
, as the number
Nof ensemble elements increases to infinity
The next step is to study the asymptotic normality of the estimation error, i.e. to prove a central limit theorem. It is somehow expected that the asymptotic variance for the ensemble Kalman
filter would be smaller than the known asymptotic variance for the different brands of particle filters, just because the ensemble Kalman filter follows essentially a parametric approach, where
only the first two empirical moments are propagated, whereas the particle filters follow a fully nonparametric approach.
Bayesian estimation in models with mean–field interactions
François
Le Gland
data assimilation
turbulent flow
Lagrangian velocity
Eulerian velocity field
simplified Langevin model
McKean model
mean–field interaction
This is a collaboration with Christophe Baehr, from the centre national de recherche météorologique (CNRM) of Météo–France.
The motivating application is the estimation of Lagrangian velocity in a turbulent flow: to filter out observation noise a Bayesian approach is used, with a simplified Langevin model
kand its dissipation rate
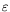 are either considered as unknown random variables, with a somehow arbitrary prior probability distribution, or are related with local Eulerian means and can then be expressed in terms of
the probability distribution of the Lagrangian velocity. In other words, the proposed simplified Langevin model is a special example of a nonlinear McKean model with mean–field interactions,
where the drift coefficient depends on the probability distribution of the solution.
are either considered as unknown random variables, with a somehow arbitrary prior probability distribution, or are related with local Eulerian means and can then be expressed in terms of
the probability distribution of the Lagrangian velocity. In other words, the proposed simplified Langevin model is a special example of a nonlinear McKean model with mean–field interactions,
where the drift coefficient depends on the probability distribution of the solution.
The original estimation problem reduces to the estimation of the hidden state in a nonlinear Markov model, and numerical approximations have been studied, with two populations of particles:
the first population of particles with mean–field interactions learns the unconditional probability distribution of the hidden state, whereas the second population of particles approximates the
Bayesian filter, i.e. the conditional probability distribution of the hidden state given the observations.
Alternatively, since noisy observations are available, the local Eulerian means can be expressed in terms of the conditional probability distribution of the Lagrangian velocity given the
observations. This results in a much simpler model, where a single population of particles is sufficient to approximate the Bayesian filter.
Design and optimization of Tardos probabilistic fingerprinting codes
Frédéric
Cérou
Teddy
Furon
Arnaud
Guyader
probability of false alarm
fingerprinting
See
Gábor Tardos
Experimental assessment of the reliability for watermarking and fingerprinting schemes
Frédéric
Cérou
Teddy
Furon
Arnaud
Guyader
probability of false alarm
ROC curve
rare event analysis
See
We introduce
Rates of convergence for nearest neighbors classification
Frédéric
Cérou
Arnaud
Guyader
classification
consistency
nonparametric statistics
This is a collaboration with Gérard Biau, from université Paris 6.
Using covering numbers for compact imbeddings in fuctional spaces, we have optained explicit rates of convergence for the
k–nearest neighbor classifier in (infinite dimensional) function spaces. The key idea is to use a norm to compute the neighbors which comes from a functional space with less regularity
than the samples. The rates obtained are genuine nonparametric convergence rates, and up to our knowledge the first of their kind for
k–nearest neighbor classification. This work is still in progress.
Contracts and Grants with Industry
Safety, complexity and responsibility based design and validation of highly automated Air Traffic Management — FP6 Aerospace project iFLY
François
Le Gland
See
INRIA contract ALLOC 2399 — May 2007 to August 2010
This FP6 project is coordinated by National Aerospace Laboratory (NLR) (The Netherlands). The academic partners are University of Cambridge and University of Leicester (United Kingdom),
Politecnico di Milano and Universita dell'Aquila (Italy), University of Twente (The Netherlands), ETH Zürich (Switzerland), University of Tartu (Estonia), National Technical University of
Athens (NTUA) and Athens University of Economics and Business (Greece), Direction des Services de la Navigation Aérienne (DSNA), École Nationale de l'Aviation Civile (ENAC), Eurocontrol
Experimental Center (EEC) and INRIA Bretagne–Atlantique (France), and the industrial partners are Honeywell (Czech Republic), Isdefe (Spain), Dedale (France), NATS En Route Ltd. (United
Kingdom).
The objective of
[iFLY]is to develop both an advanced airborne self separation design and a highly automated air traffic
management (ATM) design for en–route traffic, which takes advantage of autonomous aircraft operation capabilities and which is aimed to manage a three to six times increase in current en–route
traffic levels. The proposed research combines expertise in air transport human factors, safety and economics with analytical and Monte Carlo simulation methodologies. The contribution of ASPI
to this project concerns the work package on accident risk assessment methods and their implementation using conditional Monte Carlo methods, especially for large scale stochastic hybrid
systems: designing and studying variants
Terrain–aided navigation — contract with Thalès Communications
François
Le Gland
Nordine
El Baraka
See
INRIA contract ALLOC 2857 — January 2007 to December 2009
This collaboration with Thalès Communications is supported by DGA (Délégation Générale à l'Armement) and is related with the supervision of the CIFRE thesis of Nordine El Baraka.
The overall objective is to study innovative algorithms for terrain–aided navigation, and to demonstrate these algorithms on four different situations involving different platforms, inertial
navigation units, sensors and georeferenced databases. The thesis also considers the special use of image sensors (optical, infra–red, radar, sonar, etc.) for navigation tasks, based on
correlation between the observed image sequence and a reference image available on–board in the database.
Marginalized particle filters
Information fusion for localisation (FIL) — ANR Télécommunications
Liyun
He
François
Le Gland
See
INRIA contract ALLOC 2856 — January 2008 to December 2010
This ANR project is coordinated by Thalès Alenia Space. Academic partners are LAAS (laboratoire d'architecture et d'analyse des systèmes), TeSA consortium including ENAC (école nationale de
l'aviation civile). Industrial partners are Microtec and Silicom.
The overall objective is to study and demonstrate information fusion algorithms for localisation of pedestrian users in an indoor environment, where GPS solution cannot be used. The sought
design combines
a pedestrian dead–reckoning (PDR) unit, providing noisy estimates of the linear displacement, angular turn, and possibly of the level change through an additional
pression sensor,
range and / or proximity measurements provided by beacons at fixed and known locations, and possibly indirect distance measurements to access points, through a
measure of the power signal attenuation,
constraints provided by an indoor map of the building (map-matching),
collaborative localisation when two users meet and exchange their respective position estimates.
Besides particle methods, which are proposed as the basic information fusion algorithm for the centralized server–based implementation, simpler algorithms such as the extended Kalman filter
(EKF) or the unscented Kalman filter (UKF) are investigated, to be used for the local PDA–based implementation with a map of a smaller part of the building. In both cases, constraints are taken
care of with the help of a Voronoi graph
Security and reliability in digital watermarking (NEBBIANO) — ANR Sécurité
Frédéric
Cérou
Pierre
Del Moral
Arnaud
Guyader
See
INRIA contract ALLOC 2229 — January 2007 to December 2009.
This ANR project is coordinated by the project–team TEMICS from IRISA / INRIA Bretagne Atlantique. The other partners are LIS–INPG in Grenoble and université de Nice.
There are mainly two strategic axes in
[NEBBIANO]: watermarking and independent component analysis, and watermarking and rare event
simulations. To protect copyright owners, user identifiers are embedded in purchased content such as music or movie. This is basically what we mean by watermarking. This watermarking is to be
“invisible” to the standard user, and as difficult to find as possible. When content is found in an illegal place (e.g. a P2P network), the right holders decode the hidden message, find a
serial number, and thus they can trace the traitor, i.e. the client who has illegally broadcast their copy. However, the task is not that simple as dishonest users might collude. For security
reasons, anti–collusion codes have to be employed. Yet, these solutions (also called weak traceability codes) have a non–zero probability of error defined as the probability of accusing an
innocent. This probability should be, of course, extremely low, but it is also a very sensitive parameter: anti–collusion codes get longer (in terms of the number of bits to be hidden in
content) as the probability of error decreases. Fingerprint designers have to strike a trade–off, which is hard to conceive when only rough estimation of the probability of error is known. The
major issue for fingerprinting algorithms is the fact that embedding large sequences implies also assessing reliability on a huge amount of data which may be practically unachievable without
using rare event analysis. Our task within this project is to adapt our methods for estimating rare event probabilities to this framework, and provide watermarking designers with much more
accurate false detection probabilities than the bounds currently found in the literature. We have already applied these ideas to some randomized watermarking schemes and obtained much sharper
estimates of the probability of accusing an innocent.
Numerical investigations have been made during the internship of Vincent Bahuon (EURIA, Brest). A patent
“Validation de schémas de verrous numériques en watermarking et fingerprinting”has been submitted by INRIA and by université de Rennes 2.
Coherent detection for QPSK 40Gb systems (COHDEQ40) — ANR Télécommunications
Frédéric
Cérou
INRIA contract ALLOC 2205 — December 2006 to November 2009.
This ANR project is coordinated by Alcatel–Lucent. The other partners are Alcatel Thales III–V Lab, INT Évry, INRIA Bretagne–Atlantique (project–teams ASPI and TEMICS), Kylia, Photline and
XLIM (université de Limoges).
The project COHDEQ40 intends to demonstrate the potential of coherent detection associated with digital signal processing for the next generation high density 40Gb/s WDM systems optimized
for transparency and flexibility. Key integrated optoelectronics components and specific algorithms will be developed and system evaluation performed. The INRIA task is to develop these signal
processing algorithms needed to recover the message on the decoder side. This makes full use of our knowledge of equalization and synchronization techniques involved in digital
communications
A patent
“A decision directed algorithm for adjusting a polarization demultiplexer in a coherent detection optical receivers”has been jointly submitted in September by Alcatel Lucent and by
INRIA.
Real–time adpative coherent heterodyne detector for future optical netowrks (TCHATER) — ANR Télécommunications
Frédéric
Cérou
INRIA contract ALLOC 2801 — January 2008 to December 20010.
This ANR project is coordinated by Alcatel–Lucent. The other partners are E2V, TELECOM ParisTech, LIP (ENS Lyon).
The primary goal of the TCHATER project is to demonstrate a coherent terminal operating at 40Gb/s using
real–timedigital signal processing and efficient polarization division multiplexing. The terminal will benefit to next-generation high information-spectral density optical networks,
while offering straightforward compatibility with current 10Gbit/s networks. It will require that advanced high–speed electronic components, especially analog–to–digital converters, are
designed within the project. Specific algorithms for polarisation demultiplexing and forward error correction with soft decoding will also have to be developed.
Dissemination
Scientific animation
Arnaud Guyader is a co–organizer of the
[Séminaire de Statistiques]of the
[statistics research team]of IRMAR (institut de recherche mathématique de
Rennes).
François Le Gland has co–organized a special session on adaptive Monte Carlo methods at the
[meeting]of the MAS (modélisation aléatoire et statistique) thematic group of SMAI (société de
mathématiques appliquées et industrielles), held in Rennes in September 2008.
François Le Gland was a member of the committee for the PhD thesis of Christophe Baehr (université Paul Sabatier, Toulouse, advisor: Pierre Del Moral).
Arnaud Guyader and François Le Gland are members of the “commission de spécialistes” in applied mathematics (section 26) of université de Rennes 2. Arnaud Guyader is a member
of the “commission de spécialistes” in computer science (section 27) of université de Rennes 2. François Le Gland is a member of the “commission de spécialistes” in mathematics
(sections 25–26) of INSA (institut national de sciences appliquées) Rennes.
Teaching
François Le Gland gives a course on
[Kalman filtering and hidden Markov models], at université de Rennes 1, within the
Master SISEA (signal, image, systèmes embarqués, automatique, école doctorale MATISSE), a 3rd year course on
[Bayesian filtering and particle approximation], at ENSTA (école nationale supérieure de
techniques avancées), Paris, within the systems and control module, and a 3rd year course on hidden Markov models, at Télécom Bretagne, Brest.
Arnaud Guyader is a member of the committee of “oraux blancs d'agrégation de mathématiques” for ENS Cachan at Ker Lann.
Participation in workshops, seminars, lectures, etc.
In addition to presentations with a publication in the proceedings, and which are listed at the end of the document, members of ASPI have also given the following presentations.
Frédéric Cérou has given a talk on rare event simulation for a static distribution at the 7th international workshop on Rare Event Simulation (RESIM'08), held in Rennes in
September 2008.
Arnaud Guyader has given a talk on the rate of convergence for nearest neighbor classification at the joint meeting of the Statistical Society of Canada and the Société Française de
Statistique held in Ottawa in May 2008. He has also given a talk on rare event simulation for a static distribution at the meeting of the MAS (modélisation aléatoire et statistique)
thematic group of SMAI (société de mathématiques appliquées et industrielles), held in Rennes in September 2008.
François Le Gland has given several talks on the multilevel splitting approach to rare event simulation at the applied mathematics seminar, université Blaise Pascal, Clermont–Ferrand in
April 2008, at the 7th international workshop on Rare Event Simulation (RESIM'08), held in Rennes in September 2008, and at the LSTA (laboratoire de statistique théorique et
appliquée) seminar, université Pierre et Marie Curie in November 2008. He has given a talk on sequential data assimilation at the meeting of the GDR Turbulence et Mélange, held at CEMAGREF
in Rennes in January 2008. He has given several talks on the large sample asymptotics of the ensemble Kalman filter at the workshop on Ensemble Methods in Meteorology and Oceanography,
held at IPSL (institut Pierre–Simon Laplace) in Paris in May 2008, at the 3rd meeting on Meteorology and Applied Mathematics, held at Météo–France in Toulouse in September 2008, and
at the STAR (statistique rennaise) meeting, held at ENSAI (école nationale de la statistique et de l'analyse de l'information) in Rennes in December 2008.
Vu Duc Tran has given a talk on ensemble Kalman filter vs. particle filters at the LSTA (laboratoire de statistique théorique et appliquée) student seminar, université Pierre et Marie Curie
in March 2008.
![]() and the asymptotic variance can be estimated using an appropriate central limit theorem. To reduce the variance of the estimator, many variance reduction techniques have been proposed.
Still, running independent Monte Carlo simulations can lead to very poor results, because trajectories are generated
blindly, and only afterwards are the corresponding weights evaluated. Some of the weights can happen to be negligible, in which case the corresponding trajectories are not going to
contribute to the estimator, i.e. computing power has been wasted.
and the asymptotic variance can be estimated using an appropriate central limit theorem. To reduce the variance of the estimator, many variance reduction techniques have been proposed.
Still, running independent Monte Carlo simulations can lead to very poor results, because trajectories are generated
blindly, and only afterwards are the corresponding weights evaluated. Some of the weights can happen to be negligible, in which case the corresponding trajectories are not going to
contribute to the estimator, i.e. computing power has been wasted.![]() (
(
![]() is only defined pointwise for instance by a computer programme, and where the probability distribution of the input random variable
is only defined pointwise for instance by a computer programme, and where the probability distribution of the input random variable