New Results
Stability and Ergodicity of Piecewise Deterministic Markov Processes
Oswaldo
Costa
François
Dufour
Piecewise deterministic Markov process recurrence
ergodicity
Foster-Lyapunov criterion
The following results have been obtained in collaboration with Oswaldo Luis Do Valle Costa from Escola Politécnica da Universidade de São Paulo, Brazil. The main goal of this work published
in
X(
t)}and an embedded discrete-time Markov chain
{
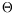
n}generated by a Markov kernel
Gthat can be explicitly characterized in terms of the three local characteristics of the PDMP, leading to tractable criteria results. First we establish some important results
characterizing
{
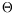
n}as a sampling of the PDMP
{
X(
t)}and deriving a connection between the probability of the first return time to a set for the discrete-time Markov chains generated by
Gand the resolvent kernel
Rof the PDMP. From these results we obtain equivalence results regarding irreducibility, existence of
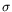 -finite invariant measures, (positive) recurrence and (positive) Harris recurrence between
{
-finite invariant measures, (positive) recurrence and (positive) Harris recurrence between
{
X(
t)}and
{
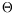
n}, generalizing the results of
Average Continuous Control of Piecewise Deterministic Markov Processes
Oswaldo
Costa
François
Dufour
Piecewise-deterministic Markov Processes
long-run average cost
optimal control
integro-differential optimality equation
vanishing approach
The long run average continuous control problem of piecewise deterministic Markov processes (PDMP's) taking values in a general Borel space and with compact action space depending on the
state variable is investigated. The control variable acts on the jump rate and transition measure of the PDMP, and the running and boundary costs are assumed to be positive but not necessarily
bounded. As far as we are aware of, this is the first time that this kind of problem is considered in the literature. Indeed, results are available for the long run average cost problem but for
impulse control see Costa
We have recently derived the following results
it has been obtained an optimality equation for the long run average cost in terms of a discrete-time optimality equation related to the embedded Markov chain given by
the post-jump location of the PDMP.
the existence of a feedback measurable selector for the discrete-time optimality equation has been shown by establishing a connection between this equation and an
integro-differential equation
sufficient conditions has been obtained for the existence of a solution for a discrete-time optimality inequality and an ordinary optimal feedback control for the long
run average cost using the so-called vanishing discount approach (see
Dynamic reliability and PDMP
Benoîte
de Saporta
François
Dufour
Yves
Dutuit
Karen
Gonzalez
Huilong
Zhang
Piecewise-deterministic Markov Processes
dynamic reliability
Monte Carlo
simulation
failure
reliability
hybrid model
The aim of the three works described in this section is to highlight the potentiality of a method which combines the high modelling ability of the piecewise deterministic Markov processes
and the great computing power inherent to the Monte Carlo simulation.
The heated tank problem is a famous case-study of dynamic reliability (see
 and liquid level
and liquid level
h. At time
t= 0, the system is in the equilibrium state where both
 and
and
hare constant,
 = 30.9261
= 30.9261
oC and
h= 7m, units 1 and 3 are on and unit 2 is off. The temperature and level evolve according to a differential equation depending on the state of the three components.
The components change state either spontaneously according to an inhomogeneous Poisson jump process whose intensity depends on the temperature, or deterministically (providing units are not
stuck) when the level reaches a lower (6m) or upper (8m) limit : in the former case, units 1 and 2 are turned on and unit 3 is turned off, in the latter case, units 1 and 2 are turned off and
unit 3 is turned on. We are interested in three possible top events : dry out (
h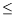 4m), overflow (
4m), overflow (
h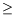 10m) or hot temperature
10m) or hot temperature

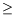 100
100
oC), and their respective cumulative probability at any time. The evolution of this hybrid system can be described by a piecewise deterministic Markov process (PDMP) with explicit
coefficients.
The aim of the work published in
We also investigated another numerical method to compute the three different failure rates. M.H.A. Davis in
Finally, a more realistic example of an offshore oil production system has been analyzed in
Optimal stopping of Piecewise Deterministic Markov Processes
Benoîte
de Saporta
François
Dufour
Karen
Gonzalez
Piecewise-deterministic Markov Processes
optimal stopping
Snell-envelope
numerical approximation
rate of convergence
We are developing a computational method for optimal stopping of a piecewise deterministic Markov process by using a quantization technique of Markov chains, see
Asymptotic behavior of bifurcating autoregressive processes
Bernard
Bercu
Benoîte
de Saporta
Anne
Gégout-Petit
bifurcating autoregressive processes
cell lineage data
binary tree
tree-indexed times series
martingales
least squares estimation
almost sure convergence
quadratic strong law
central limit theorem
Bifurcating autoregressive (BAR) processes are an adaptation of autoregressive (AR) processes to binary tree structured data. They were first introduced by Cowan and Staudte
There are several results on statistical inference and asymptotic properties of estimators for BAR models in the literature. For maximum likelihood inference on small
independent trees, see Huggins and Basawa
We have carried out a sharper analysis of the asymptotic properties of the LS estimators of the unknown parameters of first-order BAR processes and improved the previous
results of Guyon
This work has been submitted to be published
Kernel density estimation and goodness-of-fit test in adaptive tracking
Bernard
Bercu
Bruno
Portier
Estimation
Adaptive control
Kernel density estimation
Goodness-of-fit test
Since the pioneer work of Aström and Wittenmark
p,
q,
r)given, for all
n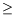 0, by
0, by
A(
R)
Xn=
B(
R)
Un+
C(
R)
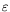
n
where
Xn,
Unand
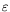
nare the
d-dimensional system output, input and driven noise, respectively. Denote by
Rthe shift-back operator and set

where
Ai,
Bj, and
Ckare unknown matrices and
Idis the identity matrice of order
d. For the sake of simplicity, we shall assume that the high frequency gain matrix
B1is known with
B1=
Id. The most common way for estimating the unknown parameter
 of the model is to make use of the extended least-squares estimator
of the model is to make use of the extended least-squares estimator
 . Moreover, the crucial role played by the control
. Moreover, the crucial role played by the control
Unis to regulate the dynamic of the process
(
X
n)by forcing
Xnto track step by step a bounded predictable reference trajectory
xn*. We make use of the standard adaptive tracking control
Unproposed by Aström and Wittenmark
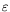
n)is a sequence of centered independent and identically distributed random vectors with positive definite covariance matrix
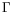 and unknown probability density function denoted by
and unknown probability density function denoted by
f.
Our goal was to study the asymptotic properties of a recursive kernel density estimator of
fgiven, for all
n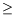 1, by
1, by

where the kernel
Kis a chosen density function and the bandwidth
(
h
n)is a sequence of positive real numbers decreasing to zero. Our purpose is first to show that
 behaves pretty well as a recursive kernel density estimator of
behaves pretty well as a recursive kernel density estimator of
fin adaptive tracking and secondly to carry out a goodness-of-fit test for
fbased on
 . Such a goodness-of-fit test is very popular in time series, in particular for testing the normality hypothesis. However, to the best of our knowledge, no work is concerned with
asymptotic properties of recursive kernel density estimator in adaptive tracking.
. Such a goodness-of-fit test is very popular in time series, in particular for testing the normality hypothesis. However, to the best of our knowledge, no work is concerned with
asymptotic properties of recursive kernel density estimator in adaptive tracking.
We provide an almost sure pointwise and uniform strong law of large numbers for
 as well as a pointwise and multivariate central limit theorem. We also carry out a goodness-of-fit test together with some simulation experiments.
as well as a pointwise and multivariate central limit theorem. We also carry out a goodness-of-fit test together with some simulation experiments.
This work has been recently published to SIAM
A new concept of strong controllability via the Schur complement in adaptive tracking
Bernard
Bercu
Victor
Vazquez
Estimation
Adaptive control
Schur complement
Central limit theorem
Law of iterated logarithm
We propose a new concept of strong controllability related to the Schur complement of a suitable limiting matrix. This new notion allows us to extend the previous convergence results
associated with multidimensional ARX models in adaptive tracking. On the one hand, we carry out a sharp analysis of the almost sure convergence for both least squares and weighted least squares
algorithms. On the other hand, we also provide a central limit theorem and a law of iterated logarithm for these two algorithms. Our asymptotic results are illustrated by numerical
simulations.
This work has been recently submitted to Automatica
Dimension reduction via Sliced Inverse Regression
Bernard
Bercu
Marie
Chavent
Vanessa
Kuentz
Benoit
Liquet
Thi Mong Ngoc
Nguyen
Jérome
Saracco
dimension reduction
sliced inverse regression
semiparametric model
Concerning the dimension reduction framework which is a useful tool for the quality control part of the project, some results have been obtained for Sliced Inverse Regression (SIR)
approach.
To reduce the dimensionality of regression problems, sliced inverse regression approaches make it possible to determine linear combinations of a set of explanatory variables
Xrelated to the response variable
Yin general semiparametric regression context. From a practical point of view, the determination of a suitable dimension (number of the linear combination of
X) is important. In the literature, statistical tests based on the nullity of some eigenvalues have been proposed. Another approach is to consider the quality of the estimation of the
effective dimension reduction (EDR) space. The square trace correlation between the true EDR space and its estimate can be used as goodness of estimation. In
 method and propose a naïve bootstrap estimation of the square trace correlation criterion. Moreover, this criterion could also select the
method and propose a naïve bootstrap estimation of the square trace correlation criterion. Moreover, this criterion could also select the
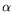 parameter in the SIR
parameter in the SIR
 method. We indicate how it can be used in practice. A simulation study is performed to illustrate the behaviour of this approach.
method. We indicate how it can be used in practice. A simulation study is performed to illustrate the behaviour of this approach.
In
Yis linked to some indices
X'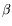
kthrough an unknown link function. SIR-I, SIR-II and SIR
 methods were introduced in order to estimate the EDR space spanned by the vectors
methods were introduced in order to estimate the EDR space spanned by the vectors
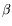
k. These methods are computationally fast and simple but are influenced by the choice of slices in the estimation process. In this paper, we suggest to use versions of SIR methods based
on fuzzy clusters instead of slices which can be seen as hard clusters and we exhibit the corresponding algorithm. We illustrate the sample behaviour of the fuzzy inverse regression estimators
and compare them with the SIR ones on simulation study.
In the theory of sufficient dimension reduction, SIR is a famous technique that enables to reduce the dimensionality of regression problems. This semiparametric regression method is based on
a linearity condition on the marginal distribution of the predictor x, which appears to be a limitation. In
In
n-consistency and asymptotic normality of the estimates. We give results from a simulation study in order to illustrate the estimation method.
More recently, Bercu, Nguyen and Saracco propose a recursive estimator for the matrices of interest in SIR approach. Moreover, when the number
Hof slices is equal to two, we obtain a recursive estimator of the direction of the parameter
 in the semiparamtric regression model
in the semiparamtric regression model
y=
f(
x' ,
,
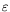 )which does not require the estimation of the link function
)which does not require the estimation of the link function
f. We give asymptotic results for this estimator. A simulation study illustrates the good numerical behaviour of this estimator for moderate sample size even if the dimension of the
covariate
xis important.
Nonparametric conditional quantile estimation
Keming
Yu
Jérome
Saracco
Mohamed
Chaouch
Ali
Gannoun
multivariate conditional quantile
geometric conditional quantile
regression model
censored data
In
In a multidimensional setting, lack of objective basis for ordering multivariate observations is a major problem in extending the notion of quantiles. Conditional quantiles are required in
various biomedical or industrial problems. Numerous alternative definitions of (conditional) quantile for multidimensional variables, have been proposed in statistical literature. In
Clustering of variables, clustering with geometrical constraints
Marie
Chavent
Vanessa
Kuentz
Jérome
Saracco
Dimension reduction via clustering of variables.Most of clustering methods have been developed for the clustering of units. Concerning variable clustering, few techniques are available.
They can however be useful for many statistical purposes : dimension reduction, selection of variables, etc. In
Clustering with geographical constraints.Agricultural policies have recently experienced major reformulations and became more and more spatialised. Agri-environmental indicators (AEIs)
provide an essential tool for formalizing information from different sources and to address the impact of agricultural production on the environment. An important political issue is currently
the implementation of WFD (Water Framework Directive) in European countries. A study is carrying out at Cemagref in the context of the
[SPICOSA project]and of the implementation of WFD ((Water Framework Directive): the purpose is to define the
relevant spatial unit, helpful for the integrated management of the continuum “Pertuis Charentais Sea” and “Charente river basin”. We have to define homogeneous areas within the Charente basin
to calculate the spatialised AEIs and to implement an hydrological model (SWAT). The goal is then to partition the hydrological units and to obtain some clusters as homogeneous as possible in
order to implement AEIs and the SWAT model. To address this problem, we have implemented a new clustering method. DIVCLUS-T is a descendant hierarchical clustering algorithm based on a
monothetic bipartitional approach allowing the dendrogram of the hierarchy to be read as a decision tree. We propose in
Interval data
Marie
Chavent
Jérome
Saracco
Uncertainty and variability are often met in practice in data concerned by quality control process. The uncertainty or the variability of the data may be treated by considering, rather than
a single value for each data, the interval of values in which it may fall. In
Air Quality
Marie
Chavent
Vanessa
Kuentz
Brigitte
Patouille
Jérome
Saracco
Air pollution is a wide concern for human health and requires the development of air quality control strategies. In order to achieve this goal pollution sources have to be accurately
identified and quantified. The case study presented in this
Interacting Markov chain Monte Carlo methods
Bernard
Bercu
Christophe
Andrieu
Pierre
Del Moral
Arnaud
Doucet
Ajay
Jasra
Markov Chain Monte Carlo
Feynman-Kac
This new line of research has been started during the period 2007-2008. It is mainly concerned with the design and the analysis of a new class of interacting stochastic algorithms for
sampling complex distributions including Boltzmann-Gibbs measures and Feynman-Kac path integral semigroups arising in physics, in biology and in advanced stochastic engineering science.
These interacting sampling methods can be described as adaptive and dynamic simulation algorithms which take advantage of the information carried by the past history to increase the quality
of the next series of samples. One critical aspect of this technique as opposed to standard Markov chain Monte Carlo methods is that it provides a natural adaptation and reinforced learning
strategy of the physical or engineering evolution equation at hand. This type of reinforcement with the past is observed frequently in nature and society, where beneficial interactions with the
past history tend to be repeated. Moreover, in contrast to more traditional mean field type particle models and related sequential Monte Carlo techniques, these stochastic algorithms can
increase the precision and performance of the numerical approximations iteratively.
The origins of these interacting sampling methods can be traced back to a pair of articles
In the period 2007-2008, these lines of research have been developed in three different directions :
The use of self-interacting Markov chain methods to Markov chain Monte Carlo methodology has been developed in a series of joint articles of C. Andrieu, P. Del Moral, A.
Doucet and A. Jasra
In a more recent article
Functional central limit theorems are developed in a pair of articles
Lm-mean error bounds in terms of the semigroup associated with the first order expansion of the limiting measure valued process, yielding what seems to be the first results of this
type for this class of interacting processes.
Feynman-Kac models and sequential Monte Carlo methods
Frédéric
Cerou
Arnaud
Guyader
Pierre
Del Moral
Arnaud
Doucet
Ajay
Jasra
Frédéric
Patras
Sylvain
Rubenthaler
Feynman-Kac
sequential Monte Carlo
nonlinear Markov chain
The design and the mathematical analysis of genetic type and branching particle interpretations of Feynman-Kac-Schroedinger type semigroups (
and vice versa) has been developed by group of researchers since the beginning of the 90's. In Bayesian statistics these sampling technology is also called sequential Monte Carlo
methods. For further details, we refer to the books
This Feynman-Kac particle methodology is increasingly identified with emerging subjects of physics, biology, and engineering science. This new theory on genetic type branching and
interacting particle systems has led to spectacular results in signal processing
During the last two decades the range of application of this modern approach to Feynman-Kac models has increased revealing unexpected applications in a number of scientific disciplines
including in :
The analysis of Dirichlet problems with boundary conditions, financial mathematics, molecular analysis, rare events and directed polymers simulation, genetic algorithms, Metropolis-Hastings
type models, as well as filtering problems and hidden Markov chains.
In the period 2007-2008, these lines of research have been developed in four different directions :
In
In
In
L2-relative error of these weighted particle measures grows linearly with respect to the time horizon yielding what seems to be the first results of this type for this class of
unnormalized models. We also illustrate these results in the context of particle simulation of static Boltzmann-Gibbs measures and restricted distributions, with a special interest in rare
event analysis.
In
Dissemination
Animation of the scientific community
B. Bercu belongs to the MAS thematic group of the SMAI.
B. Bercu is a member of the UFR council as well as a member of IMB council of the University of Bordeaux 1.
B. Bercu is the director of applied mathematic department of the University of Bordeaux 1.
M. Chavent is webmaster of the web site of the SFDS (Société Française de Statistique).
M. Chavent is a member of the scientific commitee of the following conferences EGC' 08.
M. Chavent is a member of the administration council of the SFDS (Société Française de Statistique).
P. Del Moral is an elected member of the
[International Statistical Institute since 2006].
P. Del Moral was in the MAS thematic group of the SMAI (industrial and applied mathematical society) from 2005 to 2008.
P. Del Moral is a member of the SMAI since 2005.
P. Del Moral is chief editor of the journal :
[ESAIM: Proceedings]since 2006.
P. Del Moral is an associate editor of the journal :
[Stochastic Processes and their Applications]since 2006.
P. Del Moral is an associate editor of the journal :
[Stochastic Analysis and Applications]since 2001.
P. Del Moral and Nicolas Hadjiconstantinou (MIT) are the Guest Editors M2AN for a 2010 special Volume on Probabilistic Methods.
F. Dufour is a member of the SMAI since 2007.
F. Dufour is the head of the second year cursus of the engineering school MATMECA.
F. Dufour is a member of the administration council of the engineering school MATMECA.
A. Gégout-Petit is in charge to promote the "Licence MASS" (Applied mathematics degree) of the University of Bordeaux 2 to the secondary school pupils.
A. Gégout-Petit was member of the Selection Committee (MCF 0982) for the university Victor Segalen 2009.
A. Gégout-Petit is reviewer for Journal of Statistical Planning Inference, Journal of theoretical Biology, Theoretical Biology and Medical Modelling.
A. Gégout-Petit was expert for the ANR project SYSCOMM.
B. de Saporta belongs to the MAS thematic group of the SMAI (industrial and applied mathematical society). The main purpose of this group is to promote probability and statistics in the
applied mathematic community.
B. de Saporta was a member of the Commission de Spécialistes, section 26, of the University of Bordeaux 1 in 2008.
B. de Saporta is a member of the organization commitee of Enigmath 2008, a free mathematical quizz on line for all public.
[http://
enigmath.
org/
]
B. de Saporta is a regular reviewer for
Mathematical Reviews.
J. Saracco is a member of the administration council of the SFC (Société Francophone de Classification).
J. Saracco is a member of the administration council of the University of Bordeaux 4.
J. Saracco is a reviewer for Computational Statistics and Data Analysis, Journal of Multivariate Analysis, The Annals of Statistics, Statistica Sinica, Biometrika, Comptes Rendus de
l'Académie des Sciences.
Workshop organisation
The team CQFD is very involved in the organization of the
["41e Journées de Statistique"]Annual event of the "Société Française de Statistique" which will take place in Bordeaux in 2009.
B. Bercu is the organizer of the
["Fifth Meeting of Mathematical Statistics"]between the Universities of Bordeaux, Montpellier, Santander, Valladolid, Pau, and Toulouse in June 2009.
P. Del Moral is the organizer of the first "
[Journées de Probabilités et Statistique de Bordeaux]" with the
[CEA CESTA]in october 2008. More information on this workshop is available via the web-page :
[http://
www.
math.
u-bordeaux.
fr/
~delmoral/
I-Journees.
CEA-INRIA-IMB.
html]
Participation to congresses, conferences, invitations
B. Bercu gave contributed talks at
Workshop on limit theorems, Paris, January 2008.
Alea meeting, Marseille-Luminy, March 2008.
Première Rencontre des Instituts de Mathématiques de Bordeaux, Montpellier, Pau, Toulouse, September 2008.
47e IEEE CDC Conference, Cancun, Mexico, December 2008.
Colloque CISPA Statistique des processus et Applications, Constantine, Algeria, October 2009.
F. Caron gave a contributed talk at the
[International Conference on Machine Learning], Helsinki, Finland, July 2008.
M. Chavent gave contributed talks at
AGROSTAT 2008 (10èmes journées Européennes Agro-industrie et Méthodes statistiques), Louvain-la-neuve, Belgium, January 2008.
40èmes journées de Statistique, Ottawa, June 2008.
M. Chavent gave an invited talk at COMPSTAT 08 (18th International Conference on Computational Statistics), Porto, Portugal, August 2008.
In 2008, P. Del Moral has been invited to give a series of tutorials in four national and international research programs :
[Rencontres GdR MASCOT-NUM], CEA Cadarache (March 12-14 2008). (
[3h lectures, slides to download])
[Computational Mathematics], Numerical methods in molecular simulation Bonn (April 7-11th 2008). (
[3h lectures, slides to download])
[Opening workshop, Sequential Monte Carlo Methods], SAMSI, Duke Univ. (September 7-10th 2008). (
[2h lectures, slides to download])
[10th Machine Learning summer school], Ile de Ré (September 1-15th 2008). (
[6h lectures, slides to download])
In 2008, P. Del Moral has been invited to give a series of lectures in a dozen of International Conferences and in a national colloquium :
[Colloquium du MAP5], Universite Paris Descartes, (March 28th, 2008). (
[slides to download])
[Rencontres EDP/Probas]à l'Institut Henri Poincaré, Paris (March 2008) (
[slides to download])
[Conference on Monte Carlo methods Theory and applications,]Brown University (April 25-26, 2008). (
[slides to download])
[Workshop on Probability and Statistics], Wuhan University (May 30, 2008). (
[slides to download])
[Workshop on Probability and Statistics], Capital Normal University, Beijing (June 2nd 2008). (
[slides to download])
[Colloque : Modélisation pour les Ressources Naturelles], INRA Montpellier (June 18-20 2008). (
[slides to download])
[Analysis and Probability in Nice], Nice (June 23-28 2008). (
[slides to download])
[International Workshop: Credit Risk], Evry (June 25-27 2008). (
[slides to download])
[SIAM Conference on Nonlinear Waves and Coherent Structures], session Mathematical modeling of optical communication systems, Universita di Roma La Sapienza (July 21-24 2008).
[Workshop on Numerics and Stochastics], Helsinki University (August 25-29 2008). (
[slides to download])
[Stochastic Analysis Seminar], Oxford University (December 1st, 2008).
[Stochastic Analysis Seminar], Warwick University (December 3rd, 2008).
F. Dufour gave a contributed talk at the
 -
-
 16, Avignon, October 2008.
16, Avignon, October 2008.
F. Dufour gave an invited talk to the Monash-Ritsumeikan Symposium on Probability and Related Fields, Melbourne (December 2008).
F. Dufour has been invited two weeks at Escola Politecnica, Universidade de Sao Paulo, Brasil (June, 2008).
F. Dufour has been invited two weeks at the Centre for Modelling of Stochastic Systems, Department of Mathematical Sciences, Monash University, Melbourne, Australia (December 2008).
A. Gégout-Petit gave contributed talks at
"40e journées de Statistique", Ottawa, May 2008.
"Journées MAS", Rennes, August 2008.
B. de Saporta organized a session of talks for Jounées MAS 2008 in Rennes in august.
M. Saracco gave contributed talks at
AGROSTAT 2008 (10èmes journées Européennes Agro-industrie et Méthodes statistiques), Louvain-la-neuve, Belgium, January 2008.
40èmes journées de Statistique, Ottawa, June 2008.
COMPSTAT 08 (18th International Conference on Computational Statistics), Porto, Portugal, August 2008.
Teaching
M. Chavent, A. Gégout-Petit, B. de Saporta, F. Dufour, H. Zhang, P. Del Moral, Y. Dutuit, B. Bercu and J. Saracco teach graduate probability and Statistics in the cursus "Statistique et
Fiabilité" (Statistic and Reliability) of the Master "Ingénierie Mathématique Statistique et Economique" at the Universities of Bordeaux 1, 2 and 4 .
M. Chavent and A. Gégout-Petit teach Statistic in licence MASS of University of Bordeaux 2.
A. Gégout-Petit is an academic tutor for students work experiences in company or Research Organism.
B. de Saporta teaches undergraduate mathematics and postgraduate probability and finance at the university of economics Montesquieu Bordeaux 4.
J. Saracco teaches statistics in Magistère d'Economie et de Finance Internationale (MAGEFI), University Bordeaux 4 and linear algebra and Statistics in Licence of Economics, University
Bordeaux 4.
![]() . Starting from
. Starting from
![]()
![]() , the conditional quantiles of
, the conditional quantiles of
![]() , they are used to build tolerance hyper surfaces. Finally when
, they are used to build tolerance hyper surfaces. Finally when
![]() , several parameters are studied simultaneously and multivariate or spatial conditional quantiles are used to build a tolerance region.
, several parameters are studied simultaneously and multivariate or spatial conditional quantiles are used to build a tolerance region.![]() are indeed incorporated in order to reduce the dimension of the explicative part of the model and no parametric structure is imposed on the link between
are indeed incorporated in order to reduce the dimension of the explicative part of the model and no parametric structure is imposed on the link between
![]() .
.![]() and tolerance hyper surfaces are obtained in 3D when
and tolerance hyper surfaces are obtained in 3D when
![]() .
.![]() used to reduce
used to reduce
![]() is estimated. Next, the functional parameters used in the non-parametric conditional quantile estimation are estimated. More precisely the semi-parametric approach combines the SIR
(sliced inverse regression) method and the kernel estimation of the conditional quantile. This methodology allows graphical representation of the tolerance curves in 2D (
is estimated. Next, the functional parameters used in the non-parametric conditional quantile estimation are estimated. More precisely the semi-parametric approach combines the SIR
(sliced inverse regression) method and the kernel estimation of the conditional quantile. This methodology allows graphical representation of the tolerance curves in 2D (
![]() ) or surfaces in 3D (
) or surfaces in 3D (
![]() ), with the index
), with the index
![]() easy to interpret.
easy to interpret.