Overall Objectives
Research fields
Optimizing a complex system arising from physics or engineering covers a vast spectrum in basic and applied sciences. Although we target a certain transversality from analysis to
implementation, the particular fields in which we are trying to excell can be defined more precisely.
From the
physical analysispoint of view, our expertise relies mostly on Fluid and Structural Mechanics and Electromagnetics. In the former project Sinus, some of us had contributed to the basic
understanding of fluid mechanical phenomena (Combustion, Hypersonic Non-Equilibrium Flow, Turbulence). More emphasis is now given to the coupling of engineering disciplines and to the
validation of corresponding numerical methodologies.
From the
mathematical analysispoint of view, we are concerned with functional analysis related to partial-differential equations, and the functional/algebraic analysis of numerical algorithms.
Identifying the Sobolev space in which the direct or the inverse problem makes sound sense, tailoring the numerical method to it, identifying a functional gradient in a continuous or discrete
setting, analyzing iterative convergence, improving it, measuring multi-disciplinary coupling strength and identifying critical numerical parameters, etc constitute a non-exhaustive list of
mathematical problems we are concerned with.
Regarding more specifically the
numerical aspects(for the simulation of PDEs), considerable developments have been achieved by the scientific community at large, in recent years. The areas with the closest links with
our research are:
approximation schemes, particularly by the introduction of specialized Riemann solvers for complex hyperbolic systems in Finite-Volume/Finite-Element formulations, and
highly-accurate approximations (e.g. ENO schemes),
solution algorithms, particularly by the multigrid, or multilevel and multi-domain algorithms best-equipped to overcome numerical stiffness,
parallel implementation and software platforms.
After contributing to some of these progresses in the former project Sinus, we are trying to extend the numerical approach to a more global one, including an optimization loop, and thus
contribute, in the long-term, to modern scientific computing and engineering design. We are currently dealing mostly with
geometrical optimization.
Software platformsare perceived as a necessary component to actually achieve the computational cost-efficiency and versatility necessary to master multi-disciplinary couplings required
today by size engineering simulations.
Objectives
The project has several objectives : to analyze mathematically coupled PDE systems involving one or more disciplines in the perspective of geometrical optimization or control; to
construct, analyze and experiment numerical algorithms for the efficient solution of PDEs (coupling algorithms, model reduction), or multi-criterion optimization of discretized PDEs
(gradient-based methods, evolutionary algorithms, hybrid methods, artificial neural networks, game strategies); to develop software platforms for code-coupling and for parallel and distributed
computing.
Major applications include : the multi-disciplinary optimization of aerodynamic configurations (wings in particular) in partnership with Dassault Aviation and Piaggio
Aero France; the geometrical optimization of antennas in partnership with France Télécom and Thalès Air Défense (see Opratel Virtual Lab.); the development of
Virtual Computing Environmentsin collaboration with CNES and Chinese partners (ACTRI).
Highlights of the year
A new activity has been launched by J.P. Zolesio and collaborators related to the control of Maxwell equations to locate radar targets by using a strong solution to the Hamilton-Jacobi
equation.
A new collaboration with the Numerical Simulation in Aerodynamics and Aeroacoustics Department, DSNA, of ONERA (The French Aerospace Laboratory) has been initiated by J.-A. Désidéri as a
consultant. The major areas of this collaboration are: adjoint equations for coupled aero-structural models, fast multigrid solvers for adjoint equations, global multilevel optimization,
reduced models for shape optimization and control of numerical uncertainties, game strategies for multidisciplinary optimization.
Scientific Foundations
Numerical optimization of PDE systems
Partial Differential Equations (PDEs)
finite volumes/elements
geometrical optimization
optimum shape design
multi-point/multi-criterion/multi-disciplinary optimization
shape parameterization
gradient-based/evolutionary/hybrid optimizers
hierarchical physical/numerical models
Proper Orthogonal Decomposition (POD)
Optimization problems involving systems governed by PDEs, such as optimum shape design in aerodynamics or electromagnetics, are more and more complex in the industrial setting.
In certain situations, the major difficulty resides in the costly evaluation of a functional by means of a simulation, and the numerical method to be used must exploit at
best the problem characteristics (regularity or smoothness, local convexity).
In many other cases, several criteria are to be optimized and some are non differentiable and/or non convex. A large set of parameters, sometimes of different types
(boolean, integer, real or functional), are to be taken into account, as well as constraints of various types (physical and geometrical, in particular). Additionally, today's most interesting
optimization pre-industrial projects are multi-disciplinary, and this complicates the mathematical, physical and numerical settings. Developing
robust optimizersis therefore an essential objective to make progress in this area of scientific computing.
In the area of numerical optimization algorithms, the project aims at adapting classical optimization methods (simplex, gradient, quasi-Newton) when applicable to
relevant engineering applications, as well as developing and testing less conventional approaches such as Evolutionary Strategies (ES), including Genetic or Particle-Swarm Algorithms, or hybrid
schemes, in contexts where robustness is a very severe constraint.
In a different perspective, the heritage from the former project Sinus in Finite-Volumes (or -Elements) for nonlinear hyperbolic problems, leads us to examine
cost-efficiency issues of large shape-optimization applications with an emphasis on the PDE approximation; of particular interest to us:
best approximation and shape-parameterization,
convergence acceleration (in particular by multi-level methods),
model reduction (e.g. by
Proper Orthogonal Decomposition),
parallel and grid computing; etc.
Geometrical optimization
In view of enhancing the robustness of algorithms in shape optimization or shape evolution, modeling the moving geometry is a challenging issue. The main obstacle between the geometrical
viewpoint and the numerical implementation lies in the basic fact that the shape gradients are distributions and measures lying in the dual spaces of the shape and geometrical parameters. These
dual spaces are usually very large since they contain very irregular elements. Obviously, any finite dimensional approach pertains to the Hilbert framework where dual spaces are identified
implicitly to the shape parameter spaces. But these finite-dimensional spaces sometimes mask their origin as discretized Sobolev spaces, and ignoring this question leads to well-known
instabilities; appropriate smoothing procedures are necessary to stabilize the shape large evolution. This point is sharp in the “narrow band” techniques where the lack of stability requires to
reinitialize the underlying level equation at each step.
The mathematical understanding of these questions is sought via the full analysis of the continuous modeling of the evolution. How can we “displace” a smooth geometry in
the direction opposite to a non smooth field, that is going to destroy the boundary itself, or its smoothness, curvature, and at least generate oscillations.
The notion of
Shape Differential Equationis an answer to this basic question and it arises from the functional analysis framework to be developed in order to manage the lack of duality in a
quantitative form. These theoretical complications are simplified when we return to a Hilbert framework, which in some sense, is possible, but to the undue expense of a large order of the
differential operator implied as duality operator. This operator can always be chosen as an
ad hocpower of an elliptic system. In this direction, the key point is the optimal regularity of the solution to the considered system (aerodynamical flow, electromagnetic field, etc.)
up to the moving boundary whose regularity is itself governed by the evolution process.
We are driven to analyse the fine properties concerning the minimal regularity of the solution. We make intensive use of the “extractor method” that we developed in order
to extend the I. Lasiecka and R. Triggiani “hidden regularity theory”. For example, it was well known (before this theory) that when a domain
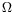 has a boundary with continuous curvatures and if a “right hand side”
has a boundary with continuous curvatures and if a “right hand side”
fhas finite energy, then the solution
uto the potential problem
-
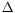
u=
fis itself in the Sobolev space
H2(
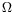 )
)
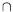
H01(
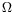 )so that the normal derivative of
)so that the normal derivative of
uat the boundary is itself square integrable. But what does this result become when the domain boundary is not smooth? Their theory permitted for example to establish that if the open set
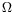 is convex, the regularity property as well as its consequences still hold. When the boundary is only a Lipschitzian continuous manifold the solution
is convex, the regularity property as well as its consequences still hold. When the boundary is only a Lipschitzian continuous manifold the solution
uloses the previous regularity. But the “hidden regularity” results developed in the 80's for hyperbolic problems, in which the
H2(
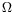 )type regularity is never achieved by the solution (regardless the
boundary regularity), do apply. Indeed
without regularity assumption on the solution
)type regularity is never achieved by the solution (regardless the
boundary regularity), do apply. Indeed
without regularity assumption on the solution
u, we proved that its normal derivative has finite energy.
In view of algorithms for shape optimization, we consider the continuous evolution
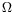
tof a geometry where
tmay be the time (governing the evolution of a PDE modeling the continuous problem); in this case, we consider a problem with dynamical geometry (non cylindrical problem) including the
dynamical free boundaries. But
tmay also be the continuous version for the discrete iterations in some gradient algorithm. Then
tis the continuous parameter for the continuous
virtualdomain deformation. The main issue is the validity of such a large evolution when
tis large, and when
t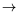
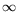 . A numerical challenge is to avoid the use of any “smoother” process and also to develop “shape-Newton” methods
. A numerical challenge is to avoid the use of any “smoother” process and also to develop “shape-Newton” methods
We denote
G(
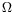 )the shape gradient of a functional
)the shape gradient of a functional
Jat
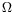 . There exists
. There exists
 such that
such that
 , where
, where
Dis the universe (or “hold all”) for the analysis. For example
 . The regularity of the domains which are solution to the shape differential equation is related to the smoothness of the
oriented distancefunction
. The regularity of the domains which are solution to the shape differential equation is related to the smoothness of the
oriented distancefunction
 which turns out to be the basic tool for intrinsic geometry. The limit case
which turns out to be the basic tool for intrinsic geometry. The limit case
 (where
(where
 is a tubular neighborhood of the boundary
is a tubular neighborhood of the boundary
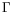 ) is the important case.
) is the important case.
If the domains are Sobolev domains, that is if
 , then we consider a duality operator,
, then we consider a duality operator,
 satisfying:
satisfying:
 where
where
Hdenotes a root space. We consider the following problem: given
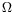 0, find a non autonomous vector field
0, find a non autonomous vector field
 such that,
such that,
Tt(
V)being the flow mapping of
V,

Several different results have been derived for this equation under
boundednessassumptions of the following kind:

The existence of such bound has first been proved for the problem of best location of actuators and sensors, and have since been extended to a large class of boundary value
problems. The asymptotic analysis (in time
t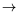
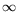 ) is now complete for a 2D problem with help of V. Sverak continuity results (and extended versions with D. Bucur). These developments necessitate an intrinsic framework in order to
avoid the use of Christoffel symbols and local mappings, and to work at
minimalregularity for the geometries.
) is now complete for a 2D problem with help of V. Sverak continuity results (and extended versions with D. Bucur). These developments necessitate an intrinsic framework in order to
avoid the use of Christoffel symbols and local mappings, and to work at
minimalregularity for the geometries.
The intrinsic geometry is the main ingredient to treat convection by a vector field
V. Such a non autonomous vector field builds up a tube. The use of
BVtopology permits these concepts to be extended to non smooth vector fields
V, thus modeling the possible topological changes. The
transverse fieldconcept
Zhas been developed in that direction and is now being applied to fluid-structure coupled problems. The most recent results have been published in three books
Integration platforms
Developing grid computing for complex applications is one of the priorities of the IST chapter in the 6th Framework Program of the European Community. One of the challenges of the 21st
century in the computer science area lies in the integration of various expertise in complex application areas such as simulation and optimisation in aeronautics, automotive and nuclear
simulation. Indeed, the design of the reentry vehicle of a space shuttle calls for aerothermal, aerostructure and aerodynamics disciplines which all interact in hypersonic regime, together with
electromagnetics. Further, efficient, reliable, and safe design of aircraft involve thermal flows analysis, consumption optimisation, noise reduction for environmental safety, using for example
aeroacoustics expertise.
The integration of such various disciplines requires powerful computing infrastructures and particular software coupling techniques. Simultaneously, advances in computer
technology militate in favour of the use of massively parallel PC-clusters including thousands of processors connected by high-speed gigabits/sec wide-area networks. This conjunction makes it
possible for an unprecedented cross-fertilisation of computational methods and computer science. New approaches including evolutionary algorithms, parameterization, multi-hierarchical
decomposition lend themselves seamlessly to parallel implementations in such computing infrastructures. This opportunity is being dealt with by the
Opaleproject since its very beginning. A software integration platform has been designed by the
Opaleproject for the definition, configuration and deployment of multidisciplinary applications on a distributed heterogeneous infrastructure
The main difficulty still remains however in the deployment and control of complex distributed applications on grids by the end-users. Indeed, the deployement of the computing grid
infrastructures and of the applications in such environments still requires specific expertise by computer science specialists. However, the users, which are experts in their particular
application fields, e.g. aerodynamics, are not necessarily experts in distributed and grid computing. Being accustomed to Internet browsers, they want similar interfaces to interact with grid
computing and problem-solving environments. A first approach to solve this problem is to define component-based infrastructures, e.g. the Corba Component Model, where the applications are
considered as connection networks including various application codes. The advantage is here to implement a uniform approach for both the underlying infrastructure and the application modules.
However, it still requires specific expertise not directly related to the application domains of each particular user. A second approach is to make use of grid services, defined as application
and support procedures to standardise access and invocation to remote support and application codes. This is usually considered as an extension of Web services to grid infrastructures. A new
approach, which is currently being explored by the
Opaleproject, is the design of a virtual computing environment able to hide the underlying grid-computing infrastructures to the users. It is
currently deployed within the Collaborative Working Environments Unit of the DG INFSO F4 of the European Commission. It is planned to include Chinese partners from the aeronautics sector in
2009 to set up a project for FP7.
Application Domains
Aeronautics and space
The demand of the aeronautical industry remains very strong in aerodynamics, as much for conventional aircraft, whose performance must be enhanced to meet new societal requirements in terms
of economy, noise (particularly during landing), vortex production near runways, etc., as for high-capacity or supersonic aircraft of the future. Our implication concerns shape optimization of
wings or simplified configurations.
Our current involvement with Space applications relates to software platforms for code coupling.
Electromagnetics
In the context of shape optimization of antennas, we can split the existing results in two parts: the two-dimensional modeling concerning only the specific transverse mode TE or TM, and
treatments of the real physical 3-D propagation accounting for no particular symmetry, whose objective is to optimize and identify real objects such as antennas.
Most of the numerical literature in shape optimization in electromagnetics belongs to the first part and makes intensive use of the 2-D solvers based on the specific 2-D
Green kernels. The 2-D approach for the optimization of
directivityled recently to serious errors due to the modeling defect. There is definitely little hope for extending the 2-D algorithms to real situations. Our approach relies on a full
analysis in unbouded domains of shape sensitivity analysis for the Maxwell equations (in the time-dependent or harmonic formulation), in particular, by using the integral formulation and the
variations of the Colton and Kreiss isomorphism. The use of the France Telecom software SR3D enables us to directly implement our shape sensitivity analysis in the harmonic approach. This
technique makes it possible, with an adequate interpolation, to retrieve the shape derivatives from the physical vector fields in the time evolution processes involving initial impulses, such
as radar or tomography devices, etc. Our approach is complementary to the “automatic differentiation codes” which are also very powerful in many areas of computational sciences. In
Electromagnetics, the analysis of hyperbolic equations requires a sound treatment and a clear understanding of the influence of space approximation.
Biology and medecine
A particular effort is made to apply our expertise in solid and fluid mechanics, shape and topology design, multidisciplinary optimization by game strategies to biology and medecine. Two
selected applications are priviledged : solid tumours and wound healing.
Opale's objective is to push further the investigation of these applications, from a mathematical-theoretical viewpoint and from a computational and software development viewpoint as well.
These studies are led in collaboration with biologists, as well as image processing specialists.
Multidisciplinary couplings
Our expertise in theoretical and numerical modeling, in particular in relation to approximation schemes, and multilevel, multiscale computational algorithms, allows us to envisage to
contribute to integrated projects focused on disciplines other than fluid dynamics or electromagnetics such as biology and virtual reality, image processing, in collaboration with specialists
of these fields.
Software
Shape optimization platform FAMOSA
Opale team is developing the platform FAMOSA, designed for shape optimization of 3D aerodynamic bodies. It integrates the following components:
a parameterization module implementing a 3D multi-level and adaptive Bézier parameterization (Free-Form Deformation) that allows to deform simultaneously the shape and
the CFD mesh ;
an optimization library composed of various algorithms, such as the Multi-directional Search Algorithm from V. Torczon (deterministic), a Particle Swarm Optimization
method (semi-stochastic) and a Kriging-based algorithm (global optimization) ;
a module managing the calls to CFD solvers ;
a metamodel library that contains tools to build a database and kriging models that are used to approximate the objective function and constraints (multi-level modelling
technique) ;
a parallel library implementing the evaluations of the objective function in parallel (independent shapes or independent flow conditions).
To facilitate the development of the software and collaborative work between the different developers, a code managing framework based on the SVN version control system has been set up. The
code is presently hosted at the inriaGforge.
The FAMOSA platform has been linked to the compressible Navier-Stokes solver NUM3SIS developed by Opale and Smash (see below), the Euler code NS3D used by Tropics for automatic
differentiation tests and the incompressible flow solver ISIS developed at the Ecole Centrale de Nantes.
Compressible Navier-Stokes solver NUM3SIS
The NUM3SIS flow solver has been developed by Smash and Opale Project-Team for two years. This work is carried out with the support of a software development engineer since October 2008 in
the framework of the ADT (Action de Développement Technologique) program.
The compressible Navier-Stokes solver has been designed for large scale parallel computations using the MPI library. Main features are:
Euler / Navier-Stokes modelling ;
Laminar / turbulent flows (Spalart-Allmaras turbulence model) ;
Multi-phase flows ;
Mixed finite-volume and finite-element spatial discretization (cell-vertex method)
High-order reconstruction schemes (MUSCL reconstruction, Beta scheme, V6 scheme)
Physical fluxes (Godunov, Van-leer flux splitting, HLLC, AUSM+)
Explicit (Backward explicit, Runge-Kutta) or implicit (Matrix-free, residuals linearization, dual time stepping);
Domain decomposition method for parallel computing.
The code has been validated on various large-scale computing facilities (Linux cluster, IBM and Bull supercomputers) for a use of several hundreds of processors.
Numerical modules for gradient computations in electromagnetics
Claude
Dedeban
France Télécom, La Turbie
Pierre
Dubois
former PhD
Jerôme
Picard
former engineer
Jean-Paul
Zolésio
Shape gradients with respect to 3D geometries in electromagnetic fields are computed by numerical code developments peripherical to the France Télécom SR3D code for the solution of the
Maxwell equations. These developments, combined with interpolation in the frequency domain, permit to compute the derivative w.r.t. the frequency.
Additionally, a self-sufficient FORTRAN code is being developed for antenna optimization by parameterized level-set techniques. This code is to be latter interfaced with the code for array
antenna optimization.
New Results
Computational methods, numerical analysis and validation
Numerical simulation of shallow-water equations
Abdou Wahidi
Bello
Jean-Antoine
Désidéri
Aurélien
Goudjo
University of Cotonou, Benin
Côme
Goudjo
University of Cotonou, Benin
Hervé
Guillard
Smash Project Team
This activity corresponds to A. W. Bello's thesis work in co-direction between the University of Cotonou, Benin, and INRIA, with the support of the French Embassy in
Cotonou. The study aims at developing a numerical simulation method of the water network in the city of Cotonou. This network includes a canal connecting Lake Nokoué to the Atlantic Ocean,
and various ducts in the city itself. This network is chronically flooded when important rains occur. In our perspective, the simulation code is meant to be used in the future as a control
tool to identify ways to prevent flood, or reduce the damages it causes.
The flow has been simulated by solving the shallow-water equations with topography and friction by a finite-volume method, as it is customary in estuary-flow-type simulations. The
computational domain is the space occupied by water and the floodplains. It is projected on a horizontal plane of reference, and discretized, and the governing equations are integrated on
each grid cell. The numerical integration is carried out by a Godunov-type scheme using a two-step Riemann approximate solver of HLLC type which preserves the positivity the water height and
which is well adapted to the treatment of the shock waves. To determine the height of the intermediate state in the Riemann solver, we propose an algorithm in a celerity-speeds formulation in
which the governing equations are linearized; as a result, the positivity of the height is preserved, and this then allows to compute the speeds of the fastest waves.
The simulation method has been tested on academic problems first to demonstrate its adequacy. Then, a more realistic case has been treated to model the phenomenon of flood in the city of
Cotonou (BENIN) by the water risings in the lagoon. The thesis was successfully defended in March
Analysis and numerical approximation of macroscopic models of vehicular traffic
Paola
Goatin
Paola Goatin is on part-time leave from University of Toulon. She is preparing her Habilitation thesis on the "Analysis and numerical approximation of some macroscopic
models of vehicular traffic". At present, she is working on a traffic flow model with phase transitions on a road network
Isogeometric analysis and design
Jean-Antoine
Désidéri
Régis
Duvigneau
Bernard
Mourrain
Galaad Project-Team
Design optimization stands at the crossroad of different scientific fields (and related software): Computer-Aided Design (CAD), Computational Fluid Dynamics (CFD) or
Computational Structural Dynamics (CSM), parametric optimization. However, these different fields are usually not based on the same geometrical representations. CAD software relies on Splines
or NURBS representations, CFD and CSM software uses grid-based geometric descriptions (structured or unstructured), optimization algorithms handle specific shape parameters. Therefore, in
conventional approaches, several information transfers occur during the design phase, yielding approximations and non-linear transformations that can significantly deteriorate the overall
efficiency of the design optimization procedure.
The isogeometric approach proposes to definitely overcome this difficulty by using CAD standards as unique representation for all disciplines. The isogeometric analysis consist in
developing methods that use NURBS representations for all design tasks:
the geometry is defined by NURBS surfaces;
the computation domain is defined by NURBS volumes instead of meshes;
the solution fields are obtained by using a finite-element approach that uses NURBS basis functions instead of classical Lagrange polynomials;
the optimizer controls directly NURBS control points.
Using such a unique data structure allows to compute the solution on the exact geometry (not a discretized geometry), obtain a more accurate solution (high-order approximation), reduce
spurious numerical sources of noise that deteriorate convergence, avoid data transfers between the software. Moreover, NURBS representations are naturally hierarchical and allows to define
multi-level algorithms for solvers as well as optimizers.
In the context of the EXCITING European project, Opale has initiated the development of a model finite-element solver based on isogeometric concepts, in collaboration with Galaad
Project-Team, to study hierarchical strategies for modelling and parameterization in this framework. This activity gives the project-team an opportunity to develop our expertise in numerical
approximation schemes for hyperbolic equations in a new application area.
Development and validation of the NUM3SIS flow solver
Praveen
Chandrashekarappa
Régis
Duvigneau
Thibaud
Kloczko
Smash Project-Team
Nikolas
Mauny
The NUM3SIS flow solver has been developed by Smash and Opale Project-Team for two years. This work has been carried out with the support of a software development
engineer since October 2008.
Some specific developments have been achieved in order to link the solver with the shape optimization platform FAMOSA and solve more complex aerodynamic problems (implementation of
Spalart-Allmaras turbulence model, dual time-stepping procedure for unsteady flows).
A study of parallel performance has been carried out on National computational facilities (IDRIS, CINES, CCRT), including computations using large grids (until 16 millions nodes for 512
processors)
Numerical algorithms for optimization and optimum-shape design
Our research themes are related to optimization and control of complex multi-disciplinary systems governed by PDEs. They include algorithmic aspects (shape
parameterization, game strategies, evolutionary algorithms, gradient/evolutionary hybridization, model reduction and hierarchical schemes), theoretical aspects (control and domain
decomposition), as well as algorithmic and software aspects (parallel and grid computing).
These general themes for Opale are given some emphasis this year through the involvement of our project in the ANR/RNTL National Network on Multi-Disciplinary Optimization "OMD”.
Hierarchical (multilevel) and adaptive shape parameterization
Badr
Abou El Majd
Jean-Antoine
Désidéri
Régis
Duvigneau
Abderrahmane
Benzaoui
Multilevel shape optimization algorithms and application to 3D aerodynamic Problems
We have proposed to exploit the classical degree–elevation process to construct a hierarchy of nested Bézier parameterizations. The construction yields in effect a
number of rigorously–embedded search spaces, used as the support of multilevel shape–optimization algorithms mimicking multigrid strategies. In particular, the most general,
FAMOSA, Full Adaptive Multilevel Optimum Shape Algorithm, is inspired by the classical
Full Multigrid Method.
The
FAMOSAmethod has been applied to the context of three–dimensional flow for the purpose of shape optimization of a transonic aircraft wing (pressure–drag minimization problem). This
complex iterative strategy has been compared with the basic one-level method, and with the simple “one-way-up” algorithm based on degree–elevation only (without coarse-parameterization
correction steps). The
FAMOSAmethod was found superior to both simpler alternatives
Multi-level parameterization algorithms have been developed also in the framework of semi-stochastic optimization methods. In particular, we have experimented with success a
Particle-Swarm Optimization (PSO) algorithm based on searches in design spaces of increasing dimension
Multi-level algorithms based on an algebraic approach
The previous hierarchical approach, based on the degree-elevation property of Bézier curves, has been extended to other parameterization types in order to be able to
solve general parametric optimization problems. The proposed approach rely on the construction of a hierarchical basis of the design space, originating from the eigenmodes of the Hessian
matrix of the cost functional.
We have experimented the method on simple analytic functions and then on shape reconstruction problems, using various approximations of the Hessian matrix (exact, finite-difference,
local metamodel, global least-squares). The application to the multidisciplinary design of a supersonic business jet (aerodynamics, structure, propulsion, flight mechanics) is currently in
progress.
Multidisciplinary optimization
Badr
Abou El Majd
now at the University of Avignon
Praveen
Chandrashekarappa
Jean-Antoine
Désidéri
Régis
Duvigneau
Vincent
Heuveline
Frank
Strauss
Abderrahmane
Habbal
Julien
Niel
Jacques
Périaux
Zhili
Tang
Nanjing University of Aeronautics and Astronautics
Multicriterion Aerodynamic Shape Design Optimization and Inverse Problems using Control Theory and Nash Games
Multicriterion design is gaining importance in Aeronautics in order to cope with new needs of society. In the literature, contributions to single discipline and/or
single-point design optimization abound. We propose to introduce a new approach combining the adjoint method with a formulation derived from game theory for multipoint aerodynamic design
problems. Transonic flows around lifting airfoils are analyzed by Euler computations. Airfoil shapes are optimized according to various aerodynamic criteria. The notion of player is
introduced. In a competitive Nash game, each player attempts to optimize its own criterion through a symmetric exchange of information with others. A Nash equilibrium is reached when each
player constrained by the strategy of the others, cannot improve further its own criterion. Specific real and virtual symmetric Nash games are implemented to set up an optimization strategy
for design under conflict.
Splitting of territories in concurrent optimization
When devising a numerical shape–optimization method in the context of a practical engineering situation, the practitioner is faced with an additional difficulty
related to the participation of several relevant physical criteria in a realistic formulation. For some problems, a solution may be found by treating all but one criteria as additional
constraints. In some other problems, mainly when the computational cost is not an issue, Pareto fronts can be identified at the expense of a very large number of functional evaluations.
However the difficulty is very acute when optimum-shape design is sought w.r.t. an aerodynamic criterion as well as other criteria for two main reasons. The first is that aerodynamics alone
is costly to analyze in terms of functional evaluation. The second is that generally only a small degradation of the performance of the absolute optimum of the aerodynamic criterion alone
is acceptable (sub–optimality) when introducing the other criteria.
We have proposed a numerical methodology for the treatment of such problems of concurrent engineering
JA, approximations of the gradient and the Hessian matrix are available or calculated using data extracted from the optimization loop itself. Then, the entire parametric space (a
subset of
 ) is split into two supplementary subspaces on the basis of a criterion related to the second variation. The construction is such that from the initial convergence point of the
primary functional, normalized perturbations of the parameters lying in one of the two subspaces, of specified dimension
) is split into two supplementary subspaces on the basis of a criterion related to the second variation. The construction is such that from the initial convergence point of the
primary functional, normalized perturbations of the parameters lying in one of the two subspaces, of specified dimension
p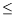
n, cause the least possible degradation to the primary functional. The latter subspace is elected to support the parameterization of a secondary functional,
JB, in a concurrent optimization realized by an algorithm simulating a Nash game between players associated with the two functionals. We prove a second result indicating that the
original global optimum point of the full-dimension primary problem is Pareto-optimal for a trivial concurrent problem. This latter result permits us to define a continuum of Nash
equilibrium points originating from the initial single-criterion optimum, in which the designer could potentially make a rational election of operating point.
First, following the thesis of B. Abou El Majd, a wing-shape aero-structural optimization was successfully realized despite the strong antagonism of the criteria in conflict in the
concurrent reduction of the wing drag in Eulerian flow and a stress integral of the structural element treated as a shell subject to linear elasticity,
Secondly, at the occasion of a two-month visit of F. Strauss, the stability of a hydrodynamic channel flow governed by the incompressible Navier-Stokes equations has been formulated
classically as a problem of control of the positivity of the real part of an appropriate eigenvalue. This case has been treated as a constrained shape optimization problem in which the
eigenvalue real part is maximized. By application of the splitting technique certain improvements of the original design have been achieved
Thirdly, J. Niel has analyzed a problem of aerodynamic design of a supersonic aircraft proposed by Dassault Aviation within the French Network on Multi-Disciplinary Optimization (OMD).
In a classical flight-mechanics model, the main flight characteristics (mass, range, take-off distance, landing velocity) are explicitly related to global aircraft design characteristics by
the fundamental laws of aerodynamics, structural and propulsion analyses. These relations have been integrated by Dassault Aviation to the Scilab project platform as explicit
functionalities of the dedicated software. J. Niel has conducted a number of optimization experiments by using these functionalities and by applying particle-swarm optimization techniquues
and territory splitting, and achieved certain viable designs
The technique of territory splitting is now being extended to encompass cases where all the criteria are of comparable importance (“equitable splits”). In a more global optimization
process under developement, the optimization is carried out in two phases. In the first, said to be “cooperative”, all the criteria under consideration are iteratively improved. In the
second phase, said to be “competitive”, viable trade-offs are identified as particular Nash equilibrium points.
Metamodel-based optimization
Praveen
Chandrashekarappa
Régis
Duvigneau
Design optimization in Computational Fluid Dynamics or Computational Structural Mechanics is particularly time consuming, since several hundreds of expensive
simulations are required in practice. Therefore, we are currently developing approaches that rely on
metamodels, i.e. models of models, in order to accelerate the optimization procedure by using different modelling levels. Metamodels are inexpensive functional value predictions that
use data computed previously and stored in a database. Different techniques of metamodelling (polynomial fitting, Radial Basis Functions, Kriging) have been developed and validated on various
engineering problems. Our developments have been particularly focused on the construction of algorithms that use both metamodels and models based on PDE's solving to drive a semi-stochastic
optimization, with various couplings
A strong coupling approach consists in using metamodels to pre-evaluate candidate designs and select those which are exactly evaluated by simulation at each iteration.
Then, the optimization algorithm relies only on exact evaluations. For the Particle-Swarm Optimization (PSO) algorithm, an adaptive method has been proposed, that allows the algorithm to
automatically adjust the number of exact evaluations required at each iteration
A weak coupling approach consists in using metamodels only to solve a set of optimization subproblems iteratively. In that case, kriging is employed to predict both
function value and modelling error. The subproblems considered (lower bound minimization, probability of improvement maximization, expected improvement maximization) indicate which
simulations should be performed to improve the model as well as determine the best design.
Uncertainty estimation and robust design
Régis
Duvigneau
Massimiliano
Martinelli
A major issue in design optimization is the capability to take uncertainties into account during the design phase. Indeed, most phenomena are subject to uncertainties,
arising from random variations of physical parameters, that can yield off-design performance losses.
To overcome this difficulty, a methodology for
robust designis currently developed and tested, that includes uncertainty effects in the design procedure, by maximizing the expectation of the performance while minimizing its
variance.
Two strategies to
propagate the uncertaintyare currently under study :
the use of metamodels to predict the uncertainties of the objective function from the uncertainties of the input parameters of the simulation tool. During the
optimization procedure, a few simulations are performed for each design variables set, for different values of the uncertain parameters in order to build a database used for metamodels
training. Then, metamodels are used to estimate some statistical quantities (expectation and variance) of the objective function and constraints, using a Monte-Carlo method.
the use of the automatic differentiation tool Tapenade (developped by Tropics Project-Team) to compute first and second order derivatives of the performance with
respect to uncertain parameters. The first order derivatives are computed by solving the adjoint system, that is built by using Tapenade in reverse mode. For the computation of the second
derivatives, two strategies can be employed: the use of two successive tangent mode differentiations or the use of the tangent mode on the result of the reverse mode differentiation. The
efficiency of these strategies depends on the number of the parameters considered. Once these derivatives have been computed, one can easily derive statistic estimations by integrating
the Taylor series expansion of the performance multiplied by the probability density function. This work is carried out in collaboration with Tropics Project-Team.
These strategies have been applied to quantify the drag statistics for a wing shape of a business aircraft subject to uncertain flow conditions (Mach number and angle of attack)
Parallel algorithms for robust aerodynamic design
Régis
Duvigneau
In order to reduce the computational time required by aerodynamic design procedures, we have developed a sophisticated parallelization strategy, that relies on a
three-level parallelization using MPI library. For a robust design optimization in aerodynamics, we compute in parallel:
the flow field using a domain decomposition approach (mesh partitionning);
the performance for different flow conditions (database filling for metamodel-based Monte-Carlo);
the performance for different candidate design (parallel optimizer).
This strategy has been applied for the robust design of a business aircraft using several hundreds of processors
Application of shape optimization algorithms to naval hydrodynamics
Régis
Duvigneau
Michel
Visonneau
CNRS, Ecole Centrale de Nantes
The shape optimization algorithms developed by Opale have been applied to challenging problems in naval hydrodynamics, in collaboration with the fluid mechanics
laboratory of Ecole Centrale de Nantes (CNRS UMR 6598).
The problem consists in optimizing the hull shape of a carrier cruise ship, with respect to two antagonistic critera : the total flow resistance and the wake caracteristics of the flow at
the propeller. Analyses are performed by solving incompressible Reynolds-averaged Navier-Stokes equations on three-dimensional unstructured grids with several millions of nodes, using the
ISIS flow solver from Ecole Centrale de Nantes. This is a particularly challenging problem because each evaluation takes several hours on a parallel machine. Moreover, complex and highly
non-linear constraints are taken into account, such as constant displacement, room for engine installation, etc. This problem was considered as test-case for a European workshop meeting
organized in Lisbon in October, where the leading naval engineering labs in Europe have competed.
Numerical shape optimization of axisymmetric radiating structures
Benoît
Chaigne
Claude
Dedeban
France Télécom R & D
Jean-Antoine
Désidéri
This activity aims at constructing efficient numerical methods for shape optimization of three-dimensional axisymmetric radiating structures incorporating and adapting
various general numerical advances
The optimization problem consists in finding the shape of the structure that minimizes a criterion related to the radiated energy. In a first formulation one aims at finding the structure
whose far field radiation fits a target radiation pattern. The target pattern can be expressed in terms of radiated power (norm of the field) or directivity (normalized power). In a second
formulation we assume that the structure is fed by a special device named the waveguide. In such a configuration one wants to reduce the so-called reflexion coefficient in the waveguide. Both
formulations make sense when the feeding is monochrome (single frequency feeding). For multiple frequencies optimization, several classical criterions used in multipoints optimization are
considered (min-max, linear combinaison, etc.).
Two models have been considered for the analysis problem: a simplified approximation model known as “Physical Optics” (PO) for which the far field is known explicitly for a given geometry;
a rigorous model based on the Maxwell equations. For the latter, the equations are solved by SRSR, a 3D solver of the Maxwell equations for axisymmetric structures provided by France Télécom
R&D.
A parametric representation of the shape based on
Free-Formdeformation (FFD) has been considered. For the PO model, the analytical gradient w.r.t. the FFD parameters has been derived. An exact Hessian has been obtained by
Automatic Differentiation (AD) using Tapenade (developed by Tropics Project-Team). Both gradient and Hessian have been validated by finite differences. For the Maxwell equations model, the
gradient is computed by finite differences.
Both global and local point of view have been considered for solving the optimization problem. An original multilevel semi-stochastic algorithm
In order to provide a theoretical basis to this multilevel method, a shape reconstruction problem has been considered. The convergence of an ideal two-level algorithm has been studied. In
a first step the matrix of the linear iteration equivalent to the bigrid cycle is computed. Then, by mean of similar transformations and with the help of Maple, the eigenvalues problem is
solved. Hence, the spectral radius of the ideal cycle is deduced. Provided that an adequate prolongation operator is used we can show the independance of the convergence rate w.r.t. the
dimension of the search space.
In addition, it has been observed that better results are obtained when the Bernstein polynomials are replaced by Legendre or Tchebychev polynomials in the FFD formulation.
In the future we intend to consider multi-objective problems together with original approaches based on game theory. Further real-case problems proposed by France Télécom will be
considered.
Application of shape and topology design to biology and medecine
Abderrahmane
Habbal
Nicholas
Ayache
Epidaure Project
Grégoire
Malandain
Epidaure Project
H.
Barelli
IPMC
B.
Mari
IPMC
In the framework of a research collaborative action COLOR 2005, involving three research teams specialized in cell biology (IPMC), image processing and mathematical
modeling (
Epidaureand
Opaleprojects), two test-cases are defined : angiogenesis and wound healing. This latter application is given particular emphasis, since experimental
results from biology can be obtained more easily.
Thus, several images and movies are quickly collected from experimental results in biology, concerning mono-layer MDCK cell healing. The analysis of these images allows us to observe that
the cell migration velocity is constant during the healing.
In order to numerically model the migration, Fisher's model (non-linear parabolic equations) seems relevant to us. Indeed, it is characterized by a constant front velocity. The first results
obtained are very promising and confirm the adequacy of Fisher's model. As a consequence of this work, new data are provided to biologists (diffusive coefficients) to describe the behavior of
MDCK cells in presence of HGF and inhibitors.
Mathematical analysis in geometrical optimization
Fast algorithm for Maxwell 3D harmonic solution via optimal control approach
Luigi
Manca
Jean-Paul
Zolésio
Using the pseudo differential boundary operator T, « Dirichlet to Neumann » for any outgoing radiating solution of the Maxwell equation in the exterior of a bounded domain D with boundary
S, we build an optimal control problem whose solution is the harmonic regime in the domain D. The optimal control is part of the initial data for the time depending solution. Under periodic
excitation (with compact support in D) and lateral Neumann boundary condition on S, the operator T is involved. The optimal synthesis involves the time backward adjoint state which is
captured by the Ricatti solution. The mathematical proof of the « device » requires sharp regularity analysis on the non homgeneous Neuman problem associated in D with the time depending 3D
Maxwell system.
Optimal geometry in radar device
Xavier
Hachair
Jean-Paul
Zolésio
This is an confidential approach for the conception of a part of radar device. It involves A specific geometrical optimization.
Hidden sharp regularity and shape derivative in wave and hyperbolic systems
Michel
Delfour
Jean-Paul
Zolésio
After IIAM 19595 in Hamburg ( and several papers) we introduced the so-called « extractor technique » which permit to recover the hidden regularity results in wave equation Under Dirichlet
Boundary Condition. These results were a kind of quantified Version of results derived by I.Lasiecka and R. Triggiani using some multiplicator techniques and were power full enough to derive
shape dérivative Under weak regularity . Nevertheless this technique failed for the Neumann like boundary conditions. We introduce theew concept of « Pseudo-differential « tehcnic which
recentely dropped this limitation. So we develop new sharp regularity results leading for shape dérivative existence for wave Under eumann boundary data in the space of finité energy on the
boundary. The intrinsic character of the pseudo extractor permits toextend easily the results to the important situation of free time depending elastic shell equations.
Non cylindrical dynamical system
Jean-Paul
Zolésio
Optimal control theory is classicaly based on the assumption that the problem to be controled has solutions and is well posed when the control parameter describes a whole set (say a
closed convex set) of some functional linear space. Concerning moving domains in classical heat or wave equations with usual boundary conditions, when the boundary speed is the control
parameter, the existence of solution is questionable. For example with homogeneous Neumann boundary conditions the existence for the wave equation is an open problem when the variation of
the boundary is not monotonic. We derive new results in which the control forces the solution to exist.
Shape optimization theory
Michel
Delfour
Jean-Paul
Zolésio
The ongoing collaboration with the CRM in Montreal (mainly with Professor Michel Delfour) led to several extensions to the theory contained in the book
Control of coupling fluid-structure devices
Marwan
Moubachir
John
Cagnol
Raja
Dziri
Jean-Paul
Zolésio
The use of the transverse vector field governed by the Lie bracket enables us to derive the “first variation” of a free boundary. This result has led to the publication of a book.
An alternate approach to fluid-structure has been developed with P.U.L.V. (J. Cagnol) and the University of Virginia (I. Lasiecka and R. Triggiani, Charlottesville)
on stabilization issues for coupled acoustic-shell modeling.
Shape gradient in Maxwell equations
Pierre
Dubois
Jean-Paul
Zolésio
It is well known that in 3D scattering, the geometrical singularities play a special role. The shape gradient in the case of such a singularity lying on a curve in 3D space has been
derived mathematically and implemented numerically in the 3D code of France Télécom.
This work with P. Dubois is potentially applicable to more general singularities.
Shape optimization by level set 3D
Claude
Dedeban
France Télécom
Pierre
Dubois
Jean-Paul
Zolésio
The
inverse scatteringproblem in electromagnetics is studied through the identification or "reconstruction" of the obstacle considered as a
smooth surfacein
R3. Through measurement of the scattered electric field
Edin a zone
 we consider the classical minimization of a functional
we consider the classical minimization of a functional
 measuring the distance beetwen
measuring the distance beetwen
Edand the actual solution
Eover
 . Then, we introduce the continuous flow mapping
. Then, we introduce the continuous flow mapping
Tr, where r is the disturbance parameter which moves the domain
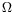 in
in
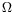
r. We derive the expression for the shape derivative of the functional, using a
minmaxformulation.
Using the Rumsey integral formulation, we solve the Maxwell equation and we compute the shape gradient, verified by finite difference, using the SR3D software (courtesy of the France
Telecom company).
Additionally, we have introduced the Level Set representation method in 3 dimensions. This technique, which comes from the image processing community, allows us to construct an
optimization method based on the shape gradient knowledge. In this method, the 3D surface, defined by a homogenous triangulation, evolves to reduce the cost functional, easily encompassing
certain topological changes. Using this technique, we have studied the inverse problem and evaluated sensibilities w.r.t. quantitative and qualitative criteria.
Shape stabilization of wave equation
Jean-Paul
Zolésio
The former results by J.P. Zolésio and C. Trucchi have been extended to more general boundary conditions in order to derive shape stabilization via the energy “cubic shape derivative”.
Further extension to elastic shell intrinsic modeling is foreseen.
Passive Shape Stabilization in wave equation
We have developed a numerical code for the simulation of the damping of the wave equation in a moving domain. The
cubic shape derivativehas been numerically verified through a new approximation taking care of the non autonomeous oprator in the order reduction technique.
Active Shape Morphing
The ongoing collaboration on the stability of wave morphing analysis for drones led to new modeling and sensitivity analyses . Any eigenmode analysis is out of the scope for moving
domains as we are faced with time depending operators. Then, we develop a new stability approach directely based ont a "Liapounov decay" by active shape control of the wave morphing. This
active control implies a backward adjoint variable and working on the linearized state ( through the
transverse vector filed
Zwhich is driven by the Lie brackets) we present a Ricatti-like synthesis for the real time of the morphing.
Array antennas optimization
Louis
Blanchard
Jean-Paul
Zolésio
We are developing a new approach for modeling array antennas optimization. This method integrates a Pareto optimization principle in order to account for the array and side lobes but
also the antenna behavior. The shape gradient is used in order to derive optimal positions of the macro elements of the array antenna.
Parametrized level set techniques
Louis
Blanchard
Jerôme
Picard
Jean-Paul
Zolésio
Since a 1981 NATO study from the University of Iowa, we know how to define the speed vector field whose flow mapping is used to build the level set of a time-dependent smooth function
F(t,x) in any dimension. We consider the Galerkin approach when F(t,.) belongs to a finite dimensional linear space of smooth functions over the fixed domain D. Choosing an appropriate
basis (eigenfunctions, special polynomials, wavelets, ...), we obtain F(t,.) as a finite expansion over the basis with time-dependent coefficients. The Hamilton-Jacobi equation for the
shape gradient descent method applied to an arbitrary shape functional (possessing a shape gradient) yields a non linear ordinary differential equation in time for these coefficients, which
are solved by the Runge-Kutta method of order four. This Galerkin approximation turns to be powerful for modeling the
topological changesduring the domains evolution. Jérome Picard has developed a code which is used by L.Blanchard (in the OpRaTel collaboration). Also they have together developed a
code for an optimal partionning procedure which is working on the same Galerkin principle but avoiding the use of calculus which would have been developed by the brut force technique.
Indeed, if the optimal partionning of a domain (e.g. an antenna) consisted in finding a decomposition by 100 subdomains, the level set approach would lead to 100 Hamilton Jacobi equations.
We introduced the concept of "multi-saddle" potential function
F(
t,
x)and through the Galerkin technique we follow the evolution of the saddle points. This technique has been succesfully understood thanks to the various testing
developed by J. Picard and will be exploited in OpRaTel collaboration by L. Blanchard and F. Neyme (Thales TAD). The work of Jérome Picard has been very interactive and very important to
understand this multi-saddle procedure which turns out to be very delicate in the parameters tuning. We developed a mathematical analysis to justify that trials-error method and some
existence results have been proved for the crossing of the singularity associated with the toplogical change in the Galerkin approximation (here the finite dimensional character is
fundamental).
Shape metrics
Louis
Blanchard
Jean-Paul
Zolésio
We characterize the geodesic for the Courant metric on Shapes. The Courant Metric is described in the book
It is extended to larger class of sets and using the
transverse flow mapping(see the book) we derive
evolution equationwhich caracterises the Geodesic for that differentiable metric.
Applications are being developed for Radar image analysis as well as for various non cylindrical evolution problems including real time control for array antennas.
Virtual computing environments
Toan
Nguyen
Based on the previous work on Virtual Computing Environments with CNES (2004-2006), the OPALE project/team is working on Virtual Collaborative Platforms which are specifically adapted to
Multiphysics Collaborative projects. This is in particular studied in the framework of the European AEROCHINA2 support action. The approach considers not only code coupling for multiphysics
applications in aeronautics, but includes also interactions between participant teams, knowledge sharing through numerical databases and communication tools using Wikies. The design of a proof
of concept demonstrator is planned in the AEROCHINA2 project, started in October 2007. Indeed, large scale multiphysics problems are expected to be orders of magnitude larger than existing
single discipline applications, like weather forcast which involve ocean and atmosphere circulation, environmental disaster prevention and emergency management. Their complexity requires new
computing technologies for the management of multi-scale and multi-physics problems, large amounts of data and heterogenous codes. Among these technologies are wide area networks and
distributed computing, using cluster and grid-based environments. It is clear that supercomputers, PC-clusters and, to a limited extent wide area grids, are currently used for demanding
e-science applications, e.g., nuclear and flight dynamics simulation. It is not so clear however what approaches are currently the best for developing multiphysics applications. We advocate the
use of an appropriate software layer called upperware, which, combined with cluster and grid-based techniques, can support virtualization of multidiscipline applications when running
multidisciplinary codes and business software, e.g., decision support tools. This paves the way for "Virtual Collaborative Platforms"
![]() has a boundary with continuous curvatures and if a “right hand side”
has a boundary with continuous curvatures and if a “right hand side”
![]()
![]() )
)
![]()
![]() )so that the normal derivative of
)so that the normal derivative of
![]() is convex, the regularity property as well as its consequences still hold. When the boundary is only a Lipschitzian continuous manifold the solution
is convex, the regularity property as well as its consequences still hold. When the boundary is only a Lipschitzian continuous manifold the solution
![]() )type regularity is never achieved by the solution (regardless the
boundary regularity), do apply. Indeed
without regularity assumption on the solution
)type regularity is never achieved by the solution (regardless the
boundary regularity), do apply. Indeed
without regularity assumption on the solution
![]()
![]()
![]() . A numerical challenge is to avoid the use of any “smoother” process and also to develop “shape-Newton” methods
. Our evolution field approaches permit to extend this viewpoint to the topological shape optimization (
).
. A numerical challenge is to avoid the use of any “smoother” process and also to develop “shape-Newton” methods
. Our evolution field approaches permit to extend this viewpoint to the topological shape optimization (
).![]() )the shape gradient of a functional
)the shape gradient of a functional
![]() . There exists
. There exists
![]() such that
such that
![]() , where
, where
![]() . The regularity of the domains which are solution to the shape differential equation is related to the smoothness of the
oriented distancefunction
. The regularity of the domains which are solution to the shape differential equation is related to the smoothness of the
oriented distancefunction
![]() which turns out to be the basic tool for intrinsic geometry. The limit case
which turns out to be the basic tool for intrinsic geometry. The limit case
![]() (where
(where
![]() is a tubular neighborhood of the boundary
is a tubular neighborhood of the boundary
![]() ) is the important case.
) is the important case.![]() , then we consider a duality operator,
, then we consider a duality operator,
![]() satisfying:
satisfying:
![]() where
where
![]() 0, find a non autonomous vector field
0, find a non autonomous vector field
![]() such that,
such that,
![]()
![]()
![]()
![]() ) is now complete for a 2D problem with help of V. Sverak continuity results (and extended versions with D. Bucur). These developments necessitate an intrinsic framework in order to
avoid the use of Christoffel symbols and local mappings, and to work at
minimalregularity for the geometries.
) is now complete for a 2D problem with help of V. Sverak continuity results (and extended versions with D. Bucur). These developments necessitate an intrinsic framework in order to
avoid the use of Christoffel symbols and local mappings, and to work at
minimalregularity for the geometries.