Overall Objectives
Overall Objectives
In recent years, a new generation of numerical algorithms have begun to spread through the scientific community. Surprisingly enough, up to a few exceptions, many of these modern ideas do
not really come from physics, but from biology and ethology. In a growing number of scientific disciplines, the researchers are now interpreting real world processes and engineering type
systems less like purely deterministic and crude clockwork mechanisms, but much more like random and sophisticated biology inspired processes. This new generation of engineering models is based
on stochastic ideas and natural principles like : Chance, randomness, interactions, reinforcement strategies, exploration rules, biology-inspired adaptation and selection transitions, learning,
reproduction, birth and death, ancestral lines and historical processes, genealogical tree evolutions, as well as self-organization principles, and many others.
These biology-inspired stochastic algorithms are often presented as natural heuristic simulation schemes without any mathematical foundations, nor a single performance analysis ensuring
their convergence, nor even a single theoretical discussion that clarifies the applicability of these models. An important aspect of our project is to create a concrete bridge between pure and
applied probability, statistics, biology, stochastic engineering and computer sciences. This fundamental bridging effort is probably one of the most important key to turn real nature's
processes into engineering devices and stochastic algorithms, by learning what can be abstracted, copied or adapted. In the reverse angle, we can mention that these abstracted models adapting
nature mechanisms and biological capabilities also provides a better understanding of the real processes.
By essence,
the team-project is not a single application-driven research project. The reasons are three folds: Firstly, the same stochastic algorithm is very often used in a variety of application
areas. On the other hand every application domain area offers a series of different perspectives that can be used to improve the design and the performances of the algorithms. Last but not
least, concrete industrial applications, as well as most of concrete problems arising in biology, physics and chemistry, require a specific attention. In general, we do not use a single class
of stochastic algorithm but a broader set of stochastic search algorithms that incorporates facets of nature inspired strategies.
Our research project is centered on two central problems in advanced stochastic engineering:
Bayesian inference and rare event simulationand more particularly
unsupervised learning, multi-target tracking, spike sorting, data assimilation and forecasting, as well as infection spreads inference.These important and natural research directions
have emerged as logical parts of the team project combined with interdisciplinary approaches well-represented at Bordeaux university campus.
The fundamental and the theoretical aspects of our research project are essentially concerned with the stochastic analysis of the following three classes of biology inspired stochastic
algorithms:
branching and interacting particle systems, reinforced random walks and self-interacting processes, random tree based models.One of our prospective research project is to apply the
Bayesian learning methodology and the recent particle filter technology to the design of a new generation of interactive
[evolutionary computation]and
[stochastic art composition]models.
Scientific Foundations
Description
This idea of analyzing nature systems and transferring the underlying principles into stochastic algorithms and technical implementations is one of the central component of the ALEA team
project. Adapting nature mechanisms and biological capabilities clearly provides a better understanding of the real processes, and it also improves the performance and the power of engineers
devices. Our project is centered on both the understanding of biological processes in terms of mathematical, physical and chemical models, and on the other hand, on the use of these biology
inspired stochastic algorithms to solve complex engineering problems.
There is a huge series of virtual interfaces, robotic devices, numerical schemes and stochastic algorithms which were invented mimicking biological processes or simulating natural
mechanisms. The terminology
"mimicking or simulating"doesn't really mean to find an exact copy of natural processes, but
to elaborate the mathematical principles so that they can be abstracted from the original biological or physical model.In our context, the whole series of evolutionary type principles
discussed in previous sections can be abstracted into only three different and natural classes of stochastic algorithms, depending on the nature of the biology-inspired interaction mechanism
used in the stochastic evolution model. These three stochastic search models are listed below :
1)
Branching and interacting particle systems ( birth and death chains, spatial branching processes, mean-field interaction between generations):
The first generation of adaptive branching-selection algorithms is very often built on the same genetic type paradigm: When exploring a state space with many particles, we duplicate better
fitted individuals at the expense of light particles with poor fitness die. From a computational point of view, we generate a large number of random problem solvers. Each one is then rated
according to a fitness or performance function defined by the developer. Mimicking natural selection, an evolutionary algorithm selects the best solvers in each generation and breeds them.
2)
Reinforced random walks and self-interacting chains (reinforced learning strategies, interaction processes with respect to the occupation measure of the past visited sites):
This type of reinforcement is observed frequently in nature and society, where "beneficial" interactions with the past history tend to be repeated. A new class of historical mean field type
interpretation models of reinforced processes were developed by the team project leader in a pair of articles
3)
Random tree based stochastic exploration models (coalescent and genealogical tree search explorations techniques on path space):
The last generation of stochastic random tree models is concerned with biology-inspired algorithms on paths and excursions spaces. These genealogical adaptive search algorithms coincide with
genetic type particle models in excursion spaces. They have been applied with success in generating the excursion distributions of Markov processes evolving in critical and rare event regimes,
as well as in path estimation and related smoothing problems arising in advanced signal processing (cf.
New Results
Bayesian Nonparametrics
François
Caron
Arnaud
Doucet
Christopher
Holmes
Jim
Griffin
Dave
Stephens
Bayesian Nonparametric Models on Decomposable Graphs
Over recent years Dirichlet processes and the associated Chinese restaurant process (CRP) have found many applications in clustering while the Indian buffet process (IBP) is increasingly
used to describe latent feature models. These models are attractive because they ensure exchangeability (over samples). We propose here extensions of these models where the dependency between
samples is given by a known decomposable graph. These models have appealing properties and can be easily learned using Markov Chain Monte Carlo and Sequential Monte Carlo techniques.
This work has been presented as an invited talk at the
[7th workshop on Bayesian nonparametrics], Turin,
Italy, and has been accepted at the NIPS international conference
Bayesian Nonparametric Models for two sample hypothesis testing
In this work
 and
and
 , with
, with
F(1),
F(2)unknown, we wish to evaluate the evidence for the null hypothesis
 verses the alternative
verses the alternative
H1:
F(1)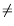
F(2). Our method is based upon a nonparametric Polya tree prior centered either
a priorior empirically. We show that the Polya tree prior allows us to calculate an analytic expression for the marginal likelihood under the two hypotheses and hence provide an explicit
measure of
 .
.
Estimation of Hölderian regularity using Genetic Programming
Leonardo
Trujillo
Pierrick
Legrand
Jacques
Levy-Vehel
Gustavo
Olague
The concept of Hölderian regularity allows us to characterize the singular structures contained within a signal
DefinitionLet
f:
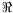
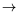
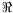 ,
,
 and
and
x0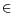
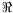 . If
. If
 , and a polynom
, and a polynom
Pof degree
<
sand a constant
cexist such that
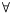
x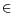
B(
x0,
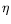 ), |
), |
f(
x)-
P(
x-
x0)|
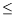
c|
x-
x0|
s,
then the pointwise Hölder exponent of
fat
x0is
 .
.
However, this exponent is very costly to estimate in the common framework (oscillations or wavelets). Therefore, we will propose a new estimator of this exponent.
Over the past two decades, Genetic Programming (GP) has proven to be a powerful paradigm for the development of computer systems that that are able to solve complex problems without the need
for substantial amounts of a priori knowledge. Indeed, GP solves two tasks simultaneously because it can search for the desired functionality and also determine the structure that the final
solutions possess. The former is achieved by using the basic principles of artificial evolution, a stochastic search process that is guided by fitness and which uses simple variation operators.
On the other hand, the latter is produced by eliminating strict structural restrictions on the evolving population that most evolutionary techniques require, as well as other black-box methods
such as neural nets
We obtained some new results listed below. 1) We studied the problem of estimating a measure of Hölderian regularity using a GP-based search, which is the first such study. 2) We have
successfully produced several operators that are capable of extracting good estimations of the pointwise Hölder exponent when compared with a canonical estimator. 3) The evolved estimators do
not require parameter tuning or design choices, because this is implicitly carried out during the optimization process. Hence, our evolved operators provide a
simpler, in this sense, estimation method.4) We have applied our evolved operators to the problem of local image description, and we show that several of them achieve a comparable
performance when compared with a canonical estimation method
Local regularity and multifractal methods for image and signal analysis
Pierrick
Legrand
We reviewed some of the important and recent applications of local regularity and multifractal analysis to signal/image processing
Interacting Markov chain Monte Carlo methods
Bernard
Bercu
Anthony
Brockwell
Pierre
Del Moral
Arnaud
Doucet
This new line of research is mainly concerned with the design and the analysis of a new class of interacting stochastic algorithms for sampling complex distributions including
Boltzmann-Gibbs measures and Feynman-Kac path integral semigroups arising in physics, in biology and in advanced stochastic engineering science. These interacting sampling methods can be
described as adaptive and dynamic simulation algorithms which take advantage of the information carried by the past history to increase the quality of the next series of samples. One critical
aspect of this technique as opposed to standard Markov chain Monte Carlo methods is that it provides a natural adaptation and reinforced learning strategy of the physical or engineering
evolution equation at hand. This type of reinforcement with the past is observed frequently in nature and society, where beneficial interactions with the past history tend to be repeated.
Moreover, in contrast to more traditional mean field type particle models and related sequential Monte Carlo techniques, these stochastic algorithms can increase the precision and performance
of the numerical approximations iteratively. The origins of these interacting sampling methods can be traced back to a pair of articles
In 2008-2009, these lines of research have been developed in three different directions :
In
In
In
 -mean error bounds in terms of the semigroup associated with the first order expansion of the limiting measure valued process, yielding what seems to be the first results of this
type for this class of interacting processes. We illustrate these results in the context of Feynman-Kac integration semigroups arising in physics, biology and stochastic engineering
science.
-mean error bounds in terms of the semigroup associated with the first order expansion of the limiting measure valued process, yielding what seems to be the first results of this
type for this class of interacting processes. We illustrate these results in the context of Feynman-Kac integration semigroups arising in physics, biology and stochastic engineering
science.
Mean field interacting particle systems
Ajay
Jasra
Frédéric
Patras
Pierre
Del Moral
Arnaud
Doucet
Sylvain
Rubenthaler
The design and the mathematical analysis of genetic type and branching particle interpretations of Feynman- Kac-Schroedinger type semigroups (and vice versa) has been developed by group of
researchers since the beginning of the 90's. In Bayesian statistics these sampling technology is also called sequential Monte Carlo methods. For further details, we refer to the books
In the period 2008-2009, these lines of research have been developed in three different directions. To develop a concrete peer to peer interaction between applied mathematics, engineering
and computer sciences, we have written two review and pedagogical book chapters on stochastic particle algorithms and their applications (
Review book chapters
In
In
Stochastic analysis
In
 -mean error bounds, and laws of large numbers for U-statistics. Applications to particle interpretations of the top eigenvalues, and the ground states of Schroedinger semigroups
are also discussed.
-mean error bounds, and laws of large numbers for U-statistics. Applications to particle interpretations of the top eigenvalues, and the ground states of Schroedinger semigroups
are also discussed.
The article
The article
New class of particle algorithms
The article
The paper
Contracts and Grants with Industry
EDF
Bernard
Bercu
François
Caron
Marie
Chavent
Pierre
Del Moral
François
Dufour
Delphine
Féral
Anne
Gégout-Petit
Frédéric
Proïa
Jérôme
Saracco
The objective of this two-year contract (140kE, 2009-2011) between the teams ALEA and CQFD and EDF - ICAME, is to develop algorithms for the recursive prediction of the electricity
consumption.
DCNS
François
Caron
Pierre
Del Moral
Michele
Pace
The objective of this contract (20kE, 2008-2009) is to give an overview of the particle Probability Hypothesis Filter for multi-target tracking in cluttered environments, and to compare
several implementations of these methods on benchmarks.
CEA
Pierre
Del Moral
Alexandru-Adrian
Tantar
Emilia
Tantar
The objective of this contract (10kE, 2009) is to implement interacting particle algorithms for the optimization of networks of sparse antenna arrays.
Sparse antenna arrays represent a topic of major interest in the electromagnetic measures domain, communications, etc., offering cost and space efficient solutions. From a formal point of
view, the optimization of a sparse antenna array, with respect to various constraints, can be modeled over a set of continuous functions, e.g. describing directivity, lobes. Nonetheless, as a
result of the non-convex and highly multi-modal nature of the functions to be optimized, classical algorithms are generally ineffective. Extending previous approaches, a Kullback-Leibler
cross-entropy based stochastic paradigm has been first considered for the study, the algorithm relying on iterative adaptive changes of the probability density functions in order to explore the
search space.
As a second part of the study, an extension has been proposed by adopting an evolutionary based approach. Different designs have been considered ranging from simple direct local search
methods to highly complex hybrid constructions, e.g. relying on island-based models of differential evolution and evolutionary algorithms. A significant improvement of the formerly obtained
results was attained, superseding the cross-entropy based approaches, previously addressed in the project. Compared to the initial solutions, the newly obtained arrays provided a higher
directivity and a reduced coupling with the enclosing environment, i.e. the objectives to be attained.
Furthermore a multi-objective formulation was introduced, in order to provide a set of good compromise (Pareto) approximate solutions. In this context a new interacting particle approach was
proposed and experimentally tested. Its performance guarantees (the convergence and quality of the offered solutions) remain to be theoretically addressed.
Other Grants and Activities
National Actions
ANR
ANR PREVASSEMBLE
This new application domain concerns the application of the particle filter technology and more general sequential Monte Carlo methods to data assimilation problems arising in
forecasting. The ALEA team project is involved in the
[ANR 2008 selected project PREVASSEMBLE]with Météo France Toulouse, the INRIA Rennes and the LMD in Paris.
ANR MODECOL
This application domain of evolutionary computing is concerned with the design of ecological systems, mixed-species models and prairial ecosystems. For more details, we refer the reader
to the web site of the
[Virtual Prairie project]The ALEA project is a partner of the 2008 ANR SYSCOM project named MODECOL.
ANR Nebbiano
The terminology watermarking refers to a set of techniques for imbedding/hiding information in a digital audio or video file, such that the change is not noticed, and very hard to
remove. In order to be used in an application, a watermarking technique must be reliable. Protection false alarms and failures of traceability codes are practically not achievable without
using rare event analysis. This application domain area of particle rare event technology is the subject of joint ANR 2007 research project with the IRISA-INRIA in Rennes and the LIS INPG
in Grenoble. For more details, we refer the reader to the website of the
[Nebbiano project. Security and Reliability in Digital Watermarking]
ANR Viroscopy
This project aims at developing stochastic mathematical models for the spread of transmissible infectious diseases, together with dedicated statistical methodologies, with the intent to
deliver efficient diagnostic/prediction tools for epidemiologists. This application domain area of particle rare event technology is the subject of joint ANR 2008 research project with
Telcom Paristech, the Laboratoire Paul Painlevé in Lille 1 and the University of Paris 5 (cf.
[Programme Systèmes Complexes et Modélisation Mathématique, list of 2008 selected projects]).
ANR Propagation
To combat dramatic event such as happened in Bombay last year (coming from the sea, a terrorist commando killed more than 200 peoples in Bombay city), authorities are decided to deploy
efficient sea surveillance system to protect coastal zone including sensitive infrastructures often in vicinity of important cities.
Regulation on frequencies allocation and on coastal constructions is strong constraint to be taken into account to install technical capabilities to permanently survey vulnerable
littoral zones. For example, new active sensor shall be frequencies compatible within numerous existing ones in inhabited region. In this context to perform coastal surveillance, attractive
solution is to deploy passive sensors networks because:
Not necessarily compatible within existing active sensors network.
Provide large possibilities to install the passive sensors, because, it is not needed to be on the shoreline, but can be deployed inside the territory. Such as
facility offers more potential sites and then, to optimise the deployment for optimal coverage of the sensitive zone.
Is totally undetectable by external technical means in hand of structured criminal organisations.
For these objectives, the PROPAGATION project will study, develop and experiment a demonstrator to carry out maritime traffic picture from a set of passive sensors: passive radar, AIS
and optronic cameras deployed over a coastal site. This is a joint ANR project with DCNS, Thalès, Ecomer and Exavision,
[accepted in 2009].
ARC INRIA
[ARC EPS]
This project aims at developing stochastic models and algorithms for the analysis of bacteriology ecosystems, especially in food safety. The objective is to predict and control critical
risk of proliferations. This is the subject of joint research project with the INRA of Paris and Montpellier, the University of Bretagne and ENV Alford.
[ARC M2A3PC]
The spread of a pathogen within a strongly anthropized perennial vegetal cover depends on many parameters acting at contrasted spatio-temporal scales. This is of paramount importance for
vine and apple trees and their airborne obligated parasites (powdery and downy mildew, scab) which strongly rely on the susceptibility and status of their hosts. Both crop systems require
from 17 to 20 fungicide treatments per year. Sustainable crop management goes through a better understanding of the dynamics of these epidemic diseases at various spatio-temporal scales.
With this in mind we aimed at developing a plant-pathogen methodology at several spatio-temporal scales. Dedicated teams from INRIA, INRA, CIRAD and CNRS research institutes joined together
to form a task force with well-known abilities on :
the overall dynamics of vine and apple tree systems studied at the desired spatio-temporal scales, in biology, epidemiology and agronomy at the plant and lanscape
scales.
modelling and 3D vizualisation of perenial plant growth coupled to development of pathogens,
mathematical modelling and numerical simulations of epidemic diseases propagation within a growing host population, including spatial spread of pathogens at different
scales.
Organization of conferences
Pierrick Legrand participated to the organization of the
[Ecole d'été EA],
Porquerolles, 2009 and the
[Journées évolutionnaires
trimestrielles](JET 19).
Pierre Del Moral and François Caron were in the organizing committee of the
[41èmes Journées de Statistiques]in Bordeaux
(May 2009, 400 participants).
International Actions
M. Pace, P. Del Moral and F. Caron organized an international workshop on
[Multi-target tracking]in
Bordeaux (25 participants).
P. Del Moral organized an international workshop on
[Stochastic Algorithms
Analysis]in Bordeaux (25 participants).
F. Caron organized an international workshop on
[Bayesian nonparametrics methods]in Whistler, Canada
(100 participants).
P. Legrand was in the organizing committee of the international conference
[EA 2009], in Strasbourg (50
participants).
Pierre Del Moral was the coordinator of an
[associate
team]with the University of Wuhan, China.
F. Caron gave an invited talk at the
[7th workshop on Bayesian nonparametrics], Turin,
Italy, 2009.
P. Del Moral in an Associate Editor of the following journals
Applied Mathematics and Optimization,
Stochastic Processes and their Applications (2006-2009),
Stochastic Analysis and Applications,
Revista de Matematica: Teoria y aplicaciones.
P. Del Moral is chief editor of the ESAIM Proceedings and guest editor of
[ESAIM M2AN].
Exterior research visitors
The following researchers visited the Team ALEA during 2009: Andreas Greven (U. Erlangen), Arnaud Doucet (UBC), Sumeetpal S. Singh (U. Cambridge), N. Whitteley (U. Bristol), B.N. Vo (U.
Melbourne), D. Laneuville (DCNS), Emmanuel Rio (U. Versailles), Jean-Pierre Vila (INRA Montpellier), Jean-Pierre Gauchi (INRA Jouy-en-Josas), Vlada Limic (CNRS), Laurent Miclo (CNRS), Arnaud
Guyader (U. Rennes), Frédéric Cérou (INRIA Rennes), Pierre Minvielle (CEA), Nicolas Champagnat (INRIA), Fabien Campillo (INRIA), Anthony Lee (U. Oxford), Shulan Hu (Wuhan University), Wu Li
Ming (U. Clermont-Ferrand), Eduardo Rodriguez Tello (CINESTAV), Aline Tabet (UBC), Zhengliang Zhang (Wuhan University), Yao Nian (Wuhan University), Arnaud Guilin (U. Clermont-Ferrand, Fuqing
Gao (Wuhan University).
Teaching
P. Del Moral gives two courses in the
[Master MIMSE]on
[Stochastic Algorithms].
F. Caron gives one course in the
[Master MIMSE]on
[Unsupervised Learning].
P. Legrand is teaching the following courses (238 hours)
Analyse Licence 1 SDV : 32H
Mathématiques générales Licence 1 SCIMS : 72H
Informatique pour les mathématiques Licence 1 SCIMS : 60H
Complément d'algèbre Licence 2 SCIMS : 72H
![]() and
and
![]() , with
, with
![]() verses the alternative
verses the alternative
![]()
![]() .
.![]()
![]()
![]() ,
,
![]() and
and
![]()
![]() . If
. If
![]() , and a polynom
, and a polynom
![]()
![]()
![]() ), |
), |
![]()
![]() .
.![]() -mean error bounds in terms of the semigroup associated with the first order expansion of the limiting measure valued process, yielding what seems to be the first results of this
type for this class of interacting processes. We illustrate these results in the context of Feynman-Kac integration semigroups arising in physics, biology and stochastic engineering
science.
-mean error bounds in terms of the semigroup associated with the first order expansion of the limiting measure valued process, yielding what seems to be the first results of this
type for this class of interacting processes. We illustrate these results in the context of Feynman-Kac integration semigroups arising in physics, biology and stochastic engineering
science.![]() -mean error bounds, and laws of large numbers for U-statistics. Applications to particle interpretations of the top eigenvalues, and the ground states of Schroedinger semigroups
are also discussed.
-mean error bounds, and laws of large numbers for U-statistics. Applications to particle interpretations of the top eigenvalues, and the ground states of Schroedinger semigroups
are also discussed.