Overall Objectives
Overall Objectives
The scientific objectives of ASPI are the design, analysis and implementation of interacting Monte Carlo methods, also known as particle methods, with focus on
statistical inference in hidden Markov models and particle filtering,
risk evaluation and simulation of rare events,
global optimization.
The whole problematic is multidisciplinary, not only because of the many scientific and engineering areas in which particle methods are used, but also because of the diversity of the
scientific communities which have already contributed to establish the foundations of the field
target tracking, interacting particle systems, empirical processes, genetic algorithms (GA), hidden Markov models and nonlinear filtering, Bayesian statistics, Markov chain
Monte Carlo (MCMC) methods, etc.
Intuitively speaking, interacting Monte Carlo methods are sequential simulation methods, in which particles
explorethe state space by mimicking the evolution of an underlying random process,
learnthe environment by evaluating a fitness function,
and
interactso that only the most successful particles (in view of the value of the fitness function) are allowed to survive and to get offsprings at the next generation.
The effect of this mutation / selection mechanism is to automatically concentrate particles (i.e. the available computing power) in regions of interest of the state space. In the
special case of particle filtering, which has numerous applications under the generic heading of positioning, navigation and tracking, in
target tracking, computer vision, mobile robotics, ubiquitous computing and ambient intelligence, sensor networks, etc.,
each particle represents a possible hidden state, and is multiplied or terminated at the next generation on the basis of its consistency with the current observation, as quantified by the
likelihood function. With these genetic–type algorithms, it becomes easy to efficiently combine a prior model of displacement with or without constraints, sensor–based measurements, and a base
of reference measurements, for example in the form of a digital map (digital elevation map, attenuation map, etc.). In the most general case, particle methods provide approximations of
Feynman–Kac distributions, a pathwise generalization of Gibbs–Boltzmann distributions, by means of the weighted empirical probability distribution associated with an interacting particle
system, with applications that go far beyond filtering, in
simulation of rare events, simulation of conditioned or constrained random variables, interacting MCMC methods, molecular simulation, etc.
The main applications currently considered are geolocalisation and tracking of mobile terminals, terrain–aided navigation, data fusion for indoor localisation, detection in sensor networks,
risk assessment in air traffic management, protection of digital documents, and credit risk estimation.
Our second research area concerns nearest neighbor estimation. This set of methods belongs to the class of supervised statistical learning algorithms. They aim at predicting some feature of
a new object from a learning
N–sample in the form of already known object–feature pairs. There are many different approches to this problem, and we decided to focus on the nearest neighbor approach, which only
considers the
knearest objects of the new one, with
ksmaller than
N, and for some given metric. Then we predict the unkown feature value by a mean on the features of the neighbors in the case of regression (continuous case), or a majority vote in the
case of classification (discrete case). Despite its simplicity, this approach works very well in practice and has led to a large amount of both applied and theoretical literature. Nevertheless,
there are still open questions, especially about the convergence of the method when the objects take values in an infinite dimensional space, or in general about the rate of convergence in
different settings, or for different choices of
k.
Scientific Foundations
Monte Carlo methods
Monte Carlo methods are numerical methods that are widely used in situations where (i) a stochastic (usually Markovian) model is given for some underlying process, and (ii) some
quantity of interest should be evaluated, that can be expressed in terms of the expected value of a functional of the process trajectory, which includes as an important special case the
probability that a given event has occurred. Numerous examples can be found, e.g. in financial engineering (pricing of options and derivative securities)
Nof the sample goes to infinity, with rate
 and the asymptotic variance can be estimated using an appropriate central limit theorem. To reduce the variance of the estimator, many variance reduction techniques have been proposed.
Still, running independent Monte Carlo simulations can lead to very poor results, because trajectories are generated
blindly, and only afterwards are the corresponding weights evaluated. Some of the weights can happen to be negligible, in which case the corresponding trajectories are not going to
contribute to the estimator, i.e. computing power has been wasted.
and the asymptotic variance can be estimated using an appropriate central limit theorem. To reduce the variance of the estimator, many variance reduction techniques have been proposed.
Still, running independent Monte Carlo simulations can lead to very poor results, because trajectories are generated
blindly, and only afterwards are the corresponding weights evaluated. Some of the weights can happen to be negligible, in which case the corresponding trajectories are not going to
contribute to the estimator, i.e. computing power has been wasted.
A recent and major breakthrough, a brief mathematical presentation of which is given in
explorethe state space under the effect of a
mutationmechanism which mimics the evolution of the underlying process,
and are
replicatedor
terminated, under the effect of a
selectionmechanism which automatically concentrates the particles, i.e. the available computing power, into regions of interest of the state space.
In full generality, the underlying process is a discrete–time Markov chain, whose state space can be
finite, continuous, hybrid (continuous / discrete), graphical, constrained, time varying, pathwise, etc.,
the only condition being that it can easily be
simulated. The very important case of a sampled continuous–time Markov process, e.g. the solution of a stochastic differential equation driven by a Wiener process or a more general Lévy
process, is also covered.
In the special case of particle filtering, originally developed within the tracking community, the algorithms yield a numerical approximation of the optimal Bayesian filter, i.e. of the
conditional probability distribution of the hidden state given the past observations, as a (possibly weighted) empirical probability distribution of the system of particles. In its simplest
version, introduced in several different scientific communities under the name of
bootstrap filter
Particle methods are currently being used in many scientific and engineering areas
positioning, navigation, and tracking
Other examples of the many applications of particle filtering can be found in the contributed volume
Particle methods are very easy to implement, since it is sufficient in principle to simulate independent trajectories of the underlying process. The whole problematic is multidisciplinary,
not only because of the already mentioned diversity of the scientific and engineering areas in which particle methods are used, but also because of the diversity of the scientific communities
which have contributed to establish the foundations of the field
target tracking, interacting particle systems, empirical processes, genetic algorithms (GA), hidden Markov models and nonlinear filtering, Bayesian statistics, Markov chain
Monte Carlo (MCMC) methods.
Particle approximations of Feynman–Kac distributions
The following abstract point of view, developed and extensively studied by Pierre Del Moral
are selected according to their respective weights (selection step),
move according to the Markov transition kernel (mutation step),
are weighted by evaluating the fitness function (weighting step).
The algorithm yields a numerical approximation of the Feynman–Kac distribution as the weighted empirical probability distribution associated with a system of particles, and many asymptotic
results have been proved as the number
Nof particles (sample size) goes to infinity, using techniques coming from applied probability (interacting particle systems, empirical processes
convergence in
Lp, convergence as empirical processes indexed by classes of functions, uniform convergence in time, see also
Beyond the simplest
bootstrapversion of the algorithm, many algorithmic variations have been proposed
are selected according to their respective weights (selection step),
move according to the proposed importance Markov transition kernel (mutation step),
are weighted by evaluating the corresponding importance function, which now depends on the Markov transition (weighting step).
Many of the early convergence results proved in the literature assume that particles are redistributed (i) using sampling with replacement and (ii) at each time step, and move
according to the original Markov transition kernel. Systematically studying the impact of the proposed algorithmic variants on the convergence results is still the subject of active
research.
Statistics of HMM
Hidden Markov models (HMM) form a special case of partially observed stochastic dynamical systems, in which the state of a Markov process (in discrete or continuous time, with finite or
continuous state space) should be estimated from noisy observations. The conditional probability distribution of the hidden state given past observations is a well–known example of a normalized
(nonlinear) Feynman–Kac distribution, see
Beyond the recursive estimation of a hidden state from noisy observations, the problem arises of statistical inference of HMM with general state space
Large time asymptotics A fruitful approach is the asymptotic study, when the observation time increases to infinity, of an extended Markov chain, whose state includes
(i) the hidden state, (ii) the observation, (iii) the prediction filter (i.e. the conditional probability distribution of the hidden state given observations at all previous time
instants), and possibly (iv) the derivative of the prediction filter with respect to the parameter. Indeed, it is easy to express the log–likelihood function, the conditional least–squares
criterion, and many other clasical contrast processes, as well as their derivatives with respect to the parameter, as additive functionals of the extended Markov chain.
The following general approach has been proposed
first, prove an exponential stability property (i.e. an exponential forgetting property of the initial condition) of the prediction filter and its derivative, for a
misspecified model,
from this, deduce a geometric ergodicity property and the existence of a unique invariant probability distribution for the extended Markov chain, hence a law of large
numbers and a central limit theorem for a large class of contrast processes and their derivatives, and a local asymptotic normality property,
finally, obtain the consistency (i.e. the convergence to the set of minima of the associated contrast function), and the asymptotic normality of a large class of minimum
contrast estimators.
This programme has been completed in the case of a finite state space
Small noise asymptotics Another asymptotic approach can also be used, where it is rather easy to obtain interesting explicit results, in terms close to the language of
nonlinear deterministic control theory
The following results have been obtained using this approach
the consistency of the maximum likelihood estimator (i.e. the convergence to the set
Mof global minima of the Kullback–Leibler divergence), has been obtained using large deviations techniques, with an analytical approach
if the abovementioned set
Mdoes not reduce to the true parameter value, i.e. if the model is not identifiable, it is still possible to describe precisely the asymptotic behavior of the estimators
rof the Fisher information matrix
Iis constant in a neighborhood of the set
M, then this set is a differentiable submanifold of codimension
r, (ii) the posterior probability distribution of the parameter converges to a random probability distribution in the limit, supported by the manifold
M, absolutely continuous w.r.t. the Lebesgue measure on
M, with an explicit expression for the density, and (iii) the posterior probability distribution of the suitably normalized difference between the parameter and its projection on
the manifold
M, converges to a mixture of Gaussian probability distributions on the normal spaces to the manifold
M, which generalized the usual asymptotic normality property,
it has been shown
I, in terms of the Kalman filter associated with the linear tangent linear Gaussian model, and (ii) the score function (i.e. the derivative of the log–likelihood function w.r.t.
the parameter), evaluated at the true value of the parameter and suitably normalized, converges to a Gaussian r.v. with zero mean and covariance matrix
I.
Multilevel splitting for rare event simulation
See
The estimation of the small probability of a rare but critical event, is a crucial issue in industrial areas such as
nuclear power plants, food industry, telecommunication networks, finance and insurance industry, air traffic management, etc.
In such complex systems, analytical methods cannot be used, and naive Monte Carlo methods are clearly unefficient to estimate accurately very small probabilities. Besides importance
sampling, an alternate widespread technique consists in multilevel splitting
Propagation of uncertainty Multilevel splitting can be used in static situations. Here, the objective is to learn the probability distribution of an output random
variable
Y=
F(
X), where the function
Fis only defined pointwise for instance by a computer programme, and where the probability distribution of the input random variable
Xis known and easy to simulate from. More specifically, the objective could be to compute the probability of the output random variable exceeding a threshold, or more generally to
evaluate the cumulative distribution function of the output random variable for different output values. This problem is characterized by the lack of an analytical expression for the function,
the computational cost of a single pointwise evaluation of the function, which means that the number of calls to the function should be limited as much as possible, and finally the complexity
and / or unavailability of the source code of the computer programme, which makes any modification very difficult or even impossible, for instance to change the model as in importance
sampling methods.
The key issue is to learn as fast as possible regions of the input space which contribute most to the computation of the target quantity. The proposed splitting methods consists in
(i) introducing a sequence of intermediate regions in the input space, implicitly defined by exceeding an increasing sequence of thresholds or levels, (ii) counting the fraction of
samples that reach a level given that the previous level has been reached already, and (iii) improving the diversity of the selected samples, usually using an artificial Markovian
dynamics. In this way, the algorithm learns
the transition probability between successive levels, hence the probability of reaching each intermediate level,
and the probability distribution of the input random variable, conditionned on the output variable reaching each intermediate level.
A further remark, is that this conditional probability distribution is precisely the optimal (zero variance) importance distribution needed to compute the probability of reaching the
considered intermediate level.
Rare event simulation To be specific, consider a complex dynamical system modelled as a Markov process, whose state can possibly contain continuous components and finite
components (mode, regime, etc.), and the objective is to compute the probability, hopefully very small, that a critical region of the state space is reached by the Markov process before a final
time
T, which can be deterministic and fixed, or random (for instance the time of return to a recurrent set, corresponding to a nominal behaviour).
The proposed splitting method consists in (i) introducing a decreasing sequence of intermediate, more and more critical, regions in the state space, (ii) counting the fraction of
trajectories that reach an intermediate region before time
T, given that the previous intermediate region has been reached before time
T, and (iii) regenerating the population at each stage, through redistribution. In addition to the non–intrusive behaviour of the method, the splitting methods make it possible to
learn the probability distribution of typical critical trajectories, which reach the critical region before final time
T, an important feature that methods based on importance sampling usually miss. Many variants have been proposed, whether
the branching rate (number of offsprings allocated to a successful trajectory) is fixed, which allows for depth–first exploration of the branching tree, but raises the
issue of controlling the population size,
the population size is fixed, which requires a breadth–first exploration of the branching tree, with random (multinomial) or deterministic allocation of offsprings,
etc.
Just as in the static case, the algorithm learns
the transition probability between successive levels, hence the probability of reaching each intermediate level,
and the entrance probability distribution of the Markov process in each intermediate region.
Contributions have been given to
minimizing the asymptotic variance, obtained through a central limit theorem, with respect to the shape of the intermediate regions (selection of the importance
function), to the thresholds (levels), to the population size, etc.
controlling the probability of extinction (when not even one trajectory reaches the next intermediate level),
designing and studying variants suited for hybrid state space (resampling per mode, marginalization, mode aggregation),
and in the static case, to
minimizing the asymptotic variance, obtained through a central limit theorem, with respect to intermediate levels, to the Metropolis kernel introduced in the mutation
step, etc.
A related issue is global optimization. Indeed, the difficult problem of finding the set
Mof global minima of a real–valued function
Vcan be replaced by the apparently simpler problem of sampling a population from a probability distribution depending on a small parameter, and asymptotically supported by the set
Mas the small parameter goes to zero. The usual approach here is to use the cross–entropy method
Nearest neighbor estimates
See
In pattern recognition and statistical learning, nearest neighbor algorithms are amongst the most simple available. Nevertheless, they are also very powerful and since the pioneering works
by Fix and Hodges
N–sample of i.i.d. object–feature pairs
(
X
i,
Y
i)for
 , with real–valued features, we want to be able to generalize, that is to guess the feature
, with real–valued features, we want to be able to generalize, that is to guess the feature
Yassociated with any new object
X, with the same probability distribution as the
Xi's. To achieve this, one chooses some integer
ksmaller than
N, and takes the mean–value of the
kfeatures associated with the
kobjects that are nearest to the new object
X, for some given metric. From the beginning it was clear that even simple, this method is very powerful.
In general, there is no way to guess exactly the value of
Y, and the minimal error that can be done is that of the Bayes estimate
![Im3 ${\#120124 [Y\#8739 X]}$](math_image_3.png) , which cannot be computed by lack of knowledge of the distribution of the pair, but the Bayes estimate will help us to characterize the strength of the method. So the best we can wish
is that our estimate converges, say when the sample size grows, to the Bayes estimate. This is what has been proved in great generality by Stone
, which cannot be computed by lack of knowledge of the distribution of the pair, but the Bayes estimate will help us to characterize the strength of the method. So the best we can wish
is that our estimate converges, say when the sample size grows, to the Bayes estimate. This is what has been proved in great generality by Stone
Xis a
d-dimensional vector,
Yis square–integrable, and the ratio
k/
Ngoes to 0. Nearest neighbor estimate is not the only local averaging estimate having this property, but it is arguably the simplest.
The situation is radically different in general infinite dimensional spaces. In this respect, Cérou and Guyader
X,
Y)cannot be dispensed with. First of all, it must be separable for the norm used to compute the neighbors, as already noticed by Cover and Hart
[page 23]. But this is not enough. By working out arguments in
Preiss
Xwith Gaussian distribution in a separable Hilbert space for which the estimate fails to be consistent. On the positive side, these authors provide a general condition, called the
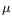 –continuity condition, which ensures the consistency of the estimate. Even with this recent results, the situation in infinite dimension is not completly clear, and this is still an
interesting field for investigation.
–continuity condition, which ensures the consistency of the estimate. Even with this recent results, the situation in infinite dimension is not completly clear, and this is still an
interesting field for investigation.
In settings for which the estimate is convergent, there is still the question of the rate of convergence, and how to choose the parameter
kin order to achive the best rate of convergence. As noticed by Kulkarni and Posner
Application Domains
Localisation, navigation and tracking
See
Among the many application domains of particle methods, or interacting Monte Carlo methods, ASPI has decided to focus on applications in localisation (or positioning), navigation and
tracking
a prior dynamical model of typical evolutions of the mobile, such as inertial estimates and prior model for inertial errors,
measurements provided by sensors,
and possibly a digital map providing some useful feature (terrain altitude, power attenuation, etc.) at each possible position.
In some applications, another useful source of information is provided by
a map of constrained admissible displacements, for instance in the form of an indoor building map,
which particle methods can easily handle (map-matching). This Bayesian dynamical estimation problem is also called filtering, and its numerical implementation using particle methods, known
as particle filtering, has been introduced by the target tracking community
target tracking, integrated navigation, points and / or objects tracking in video sequences, mobile robotics, wireless communications, ubiquitous computing and ambient
intelligence, sensor networks, etc.
ASPI is contributing to several applications of particle filtering in positioning, navigation and tracking, such as geolocalisation and tracking in a wireless network, terrain–aided
navigation, see
Rare event simulation
See
Another application domain of particle methods, or interacting Monte Carlo methods, that ASPI has decided to focus on is the estimation of the small probability of a rare but critical event,
in complex dynamical systems. This is a crucial issue in industrial areas such as
nuclear power plants, food industry, telecommunication networks, finance and insurance industry, air traffic management, etc.
In such complex systems, analytical methods cannot be used, and naive Monte Carlo methods are clearly unefficient to estimate accurately very small probabilities. Besides importance
sampling, an alternate widespread technique consists in multilevel splitting
ASPI is contributing to several applications of multilevel splitting for rare event simulation, such as risk assessment in air traffic management, see
New Results
Rate of convergence of the bagged nearest neighbor estimate
Frédéric
Cérou
Arnaud
Guyader
See
This is a collaboration with Gérard Biau, from université Pierre et Marie Curie, ENS Paris and INRIA Paris Rocquencourt (project–team CLASSIC).
Bagging is a simple way to combine estimates in order to improve their performance. This method, suggested by Breiman in 1996, proceeds by resampling from the original data set, constructing
a predictor from each subsample, and decide by combining. By bagging an
n-sample, the crude nearest neighbor regression estimate is turned into a consistent weighted nearest neighbor regression estimate, which is amenable to statistical analysis. Letting the
resampling size
kngrows with
nin such a manner that
kn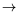
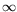 and
and
kn/
n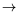 0, we have shown that this estimate achieves optimal rate of
convergence, independently from the fact that resampling is done with or without replacement. Since the estimate with the optimal rate of convergence depends on the unknown distribution of the
observations, adaptation results by data–splitting are also obtained
0, we have shown that this estimate achieves optimal rate of
convergence, independently from the fact that resampling is done with or without replacement. Since the estimate with the optimal rate of convergence depends on the unknown distribution of the
observations, adaptation results by data–splitting are also obtained
Rates of convergence of the functional
k–nearest neighbor estimate
Frédéric
Cérou
Arnaud
Guyader
See
This is a collaboration with Gérard Biau, from université Pierre et Marie Curie, ENS Paris and INRIA Paris Rocquencourt (project–team CLASSIC).
Motivated by a broad range of potential applications, such as regression on curves, we investigate rates of convergence of the
k-nearest neighbor estimate of the regression function, based on
Nindependent copies of the pair
(
X,
Y), when
Xis in a suitable ball in some functional space. Using compact embedding theory, we present explicit and general finite sample bounds on the expected squared difference between
k-nearest neighbor estimator and Bayes regression function, in a very general setting. We also particularize our results to classical function spaces such as Sobolev spaces, Besov spaces
and reproducing kernel Hilbert spaces. The rates obtained are genuine nonparametric convergence rates, and up to our knowledge the first of their kind for
k–nearest neighbor regression
Estimating the minimal length of Tardos code
Frédéric
Cérou
Arnaud
Guyader
See
This is a collaboration with Luis Pérez–Feire from GRADIANT (Galician R&D Center in Advanced Telecommunications, Vigo, Spain) and with Teddy Furon from INRIA Rennes Bretagne Atlantique
(project–team TEMICS).
We are interested in the minimal length of a binary probabilistic traitor tracing code. We consider the code construction proposed by Gábor Tardos in 2003, with the symmetric accusation
function as improved by Boris Škorić et al. The length estimation is based on two pillars. First, we consider the worst case attack that a group of
ccolluders can lead. This attack minimizes the mutual information between the code sequence of a colluder and the pirated sequence. Second, an algorithm pertaining to the field of rare
event analysis is constructed in order to estimate the probabilities of error: the probability that an innocent user is framed, and the probabilities that all colluders are missed. Therefore,
for a given collusion size, we are able to estimate the minimal length of the code satisfying some error probabilities constraints
Estimating the probability of false alarm for a zero–bit watermarking technique
Frédéric
Cérou
Arnaud
Guyader
Cyrille
Jégourel
See
This is a collaboration with Teddy Furon from INRIA Rennes Bretagne Atlantique (project–team TEMICS).
Assessing that a probability of false alarm is below a given significance level is a crucial issue in watermarking. We have proposed an iterative and self–adapting algorithm which estimates
very low probabilities of error. Some experimental investigations validates its performance for a rare detection scenario where there exists a close form formula of the probability of false
alarm. Our algorithm appears to be much quicker and more accurate than a classical Monte Carlo estimator. It even allows the experimental measurement of error exponents
Credit risk estimation
Frédéric
Cérou
Arnaud
Guyader
See
We applied our rare event techniques to the Credit Metrics model in order to estimate the probability of large loss. We found that at least on this Gaussian model, our methods compares well
with state of the art importance sampling techniques, as proposed by Glasserman et al.
Rare event techniques for integral estimation
Frédéric
Cérou
Arnaud
Guyader
Jean-Baptiste
Le Meur
See
This is a collaboration with Éric Matzner–Løber, from université de Rennes 2.
We applied our rare event techniques to the estimation of integrals that are too complicated to be computed by either numerical methods, or Monte Carlo. Typically, one can think of the
partition function of a Gibbs measure. Very preliminary results indicate that the proposed method may prove very useful for some difficult cases. This is still a work in progress.
Particle methods with adaptive resampling
François
Le Gland
This is a collaboration with Élise Arnaud, from université Joseph Fourier and INRIA Grenoble Rhône Alpes (project–team PERCEPTION).
A longstanding problem in particle or sequential Monte Carlo (SMC) methods is to mathematically prove the popular belief that resampling does improve the performance of the estimation (this
of course is not always true, and the real question is to clarify classes of problems where resampling helps). A more pragmatic answer to the problem is to use adaptive procedures that have
been proposed on the basis of heuristic considerations, where resampling is performed only when it is felt necessary, i.e. when some criterion (effective number of particles, entropy of the
sample, etc.) reaches some prescribed threshold. It still remains to mathematically prove the efficiency of such adaptive procedures. Our first contribution has been to consider a design where
resampling is performed at some intermediate fixed time instants, and to optimize the asymptotic variance of the estimation error w.r.t. the resampling time instants. The second
contribution
Non–parametric learning of the optimal importance distribution
François
Le Gland
This is a collaboration with Nadia Oudjane, from EDF R&D Clamart.
Evaluating an integral or a mathematical expectation of a nonnegative function can always be seen as computing the normalization constant in a Boltzmann–Gibbs probability distribution. When
the probability distribution and the nonnegative function do not agree, i.e. have significant contributions in different parts of the integration space, then the variance of the estimator can
be very large, and one should use another importance distribution, ideally the optimal (zero variance) importance distribution
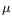 *which unfortunately cannot be used since it depends on the desired (but unknown) integral. Alternatively, sequential methods have been designed (under different names, such as annealed
sampling, progressive correction, multilevel splitting, etc., depending on the context) which not only provide an expression for the desired integral as the product of intermediate
normalization constants, but ultimately provide as well an
*which unfortunately cannot be used since it depends on the desired (but unknown) integral. Alternatively, sequential methods have been designed (under different names, such as annealed
sampling, progressive correction, multilevel splitting, etc., depending on the context) which not only provide an expression for the desired integral as the product of intermediate
normalization constants, but ultimately provide as well an
N–sample approximately distributed according to the optimal importance distribution. From the weighted empirical probability distribution associated with this sample, a regularized
probability distribution
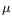
Ncan be obtained, using a kernel method or a simple histogram, and can be used as an almost optimal importance distribution to estimate the original integral with a
M–sample distributed according to
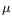
N. The variance of the resulting estimator depends on the product of the inverse sample size
1/
Mby the
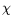 2–distance between the almost optimal importance distribution
2–distance between the almost optimal importance distribution
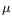
Nand the optimal (zero variance) importance distribution
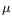 *.
*.
Our contribution has been to provide an estimate of this
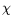 2–distance, under mild assumptions. The impact of dimension on density estimation is a limiting factor here, but the variance reduction is very significant in moderate dimensions.
2–distance, under mild assumptions. The impact of dimension on density estimation is a limiting factor here, but the variance reduction is very significant in moderate dimensions.
Estimation of extreme quantiles and isoquantile curves
François
Le Gland
Rudy
Pastel
See
This is a collaboration with Jérôme Morio, from ONERA Châtillon.
Many reliability or hedging problems reduce to quantile estimation, and increasing safety standards creates a need for extreme quantile estimation. Adaptive multilevel splitting methods are
studied in this context, which significantly reduce the variance of the relative error. A multilevel definition of quantile is proposed, under the name of isoquantile curves and is compared
with the classical definition in terms of circular error probables. Its main advantage is a better use of the angular distribution, as illustrated in an example regarding the impact location of
a ballistic launcher.
Path planning for navigation in a geographic information system
Jean–Pierre
Le Cadre
Francis
Céleste
The problem we considered is the optimization of the navigation of an intelligent mobile in a real world environment, described by a map. The map is composed of features representing natural
landmarks in the environment. The vehicle is equipped with sensors which allows it to obtain landmark parameter estimates. These measurements are correlated with the map so as to estimate the
mobile position. The optimal trajectory must be designed in order to control a measure of the performance for the filtering algorithm used for mobile navigation. As the mobile state and the
measurements are random, a well–suited measure can be a functional of the posterior Cramer–Rao bound (PCRB). In many applications, it is crucial to be able to estimate accurately the state of
the mobile during the execution of the plan. So it is necessary to couple the planning and the execution stages.
A classical tool is the constrained Markov decision process (MDP) framework. However, our optimality criterion is based on the posterior Cramer–Rao bound, and the nature of the objective
function for path planning makes it impossible to perform complete optimization within the MDP framework. Indeed, the reward in one stage of our MDP depends on all the history of the
trajectory. To overcome this problem, the cross–entropy method
Extracting information from a video sensor network
Jean–Pierre
Le Cadre
Adrien
Ickowicz
See
Recent trends lead to consider globally networks of (video) sensors. These networks can be relatively large, so we have to face specific problems. How can we use the data at the sensor
level, how to represent the information collected at the sensor level, how to fuse ? A first step consists in extracting spatio–temporal informations from video sensors. Of course, these
sensors are generally uncalibrated and asynchronous. So we have to consider rather rough informations. Roughness can go up to reduce the information to proximity and to a binary information
about object motion (closing or not). A first step has been to consider the use of the estimated closest point of approach (CPA) times for estimating the parameters of the target trajectories.
This study is relatively simple but has the great advantage to put in evidence the basic requirements and the limits of this approach. In a second step, we considered the estimation of the CPA
times from a sequence of images.
The limits of the above approach are quite obvious. If it is able to exploit a temporal contrast, there is a strong need to use a spatio–temporal contrast at the (binary) sensor network
level. Actually, it has been shown that the separation problem we have to solve present strong similarities with the optimization problems we have to solve in a SVM context. The benefits of
this approach are multiple: it is well adapted to (robust) tracking and the combinatorial problems which plagued multitarget tracking are fundamentally reduced. For the tracking step, particle
filtering is the natural way since it can easily include complex priors, non–linear measurements as well as separation properties, within a hierarchical context. Our contribution this year has
been a first step towards multiple target tracking within this framework
Contracts and Grants with Industry
Safety, complexity and responsibility based design and validation of highly automated air traffic management (iFLY) — FP6 Aerospace
François
Le Gland
See
INRIA contract ALLOC 2399 — May 2007 to August 2010.
This FP6 project is coordinated by National Aerospace Laboratory (NLR) (The Netherlands). The academic partners are University of Cambridge and University of Leicester (United Kingdom),
Politecnico di Milano and Universita dell'Aquila (Italy), University of Twente (The Netherlands), ETH Zürich (Switzerland), University of Tartu (Estonia), National Technical University of
Athens (NTUA) and Athens University of Economics and Business (Greece), Direction des Services de la Navigation Aérienne (DSNA), École Nationale de l'Aviation Civile (ENAC), Eurocontrol
Experimental Center (EEC) and INRIA Rennes Bretagne Atlantique (France), and the industrial partners are Honeywell (Czech Republic), Isdefe (Spain), Dedale (France), NATS En Route Ltd. (United
Kingdom).
The objective of
[iFLY]is to develop both an advanced airborne self separation
design and a highly automated air traffic management (ATM) design for en–route traffic, which takes advantage of autonomous aircraft operation capabilities and which is aimed to manage a three
to six times increase in current en–route traffic levels. The proposed research combines expertise in air transport human factors, safety and economics with analytical and Monte Carlo
simulation methodologies. The contribution of ASPI to this project concerns the work package on accident risk assessment methods and their implementation using conditional Monte Carlo methods,
especially for large scale stochastic hybrid systems: designing and studying variants
Terrain–aided navigation — contract with Thalès Communications
François
Le Gland
Nordine
El Baraka
See
INRIA contract ALLOC 2857 — September 2007 to August 2010.
This collaboration with Thalès Communications is supported by DGA (Délégation Générale à l'Armement) and is related with the supervision of the CIFRE thesis of Nordine El Baraka.
The overall objective is to study innovative algorithms for terrain–aided navigation, and to demonstrate these algorithms on four different situations involving different platforms, inertial
navigation units, sensors and georeferenced databases. The thesis also considers the special use of image sensors (optical, infra–red, radar, sonar, etc.) for navigation tasks, based on
correlation between the observed image sequence and a reference image available on–board in the database.
Marginalized particle filters
Optimization of sensors location and activation — contract with DGA / CTSN (centre technique des systèmes navals)
Jean–Pierre
Le Cadre
François
Le Gland
See
INRIA contract ALLOC 4233 — April 2009 to March 2011.
This is a collaboration with Sébastien Paris, from université Paul Cézanne, related with the supervision of the PhD thesis of Mathieu Chouchane.
The objective of this project is to optimize the position and activation times of a few sensors deployed by a platform over a search zone, so as to maximize the probability of detecting a
moving target. The difficulty here is that the target can detect an activated sensor before it is detected itself, and it can then modify its own trajectory to escape from the sensor. Because
of the many constraints including timing constraints involved in this optimization problem, a stochastic algorithm is preferred here over a deterministic algorithm. The underlying idea is to
replace the problem of maximizing a cost function (the probability of detection) over the possible configurations (admissible position and activation times) by the apparently simpler problem of
sampling a population according to a probability distribution depending on a small parameter, which asymptotically concentrates on the set of global maxima of the cost function, as the small
parameter goes to zero. The usual approach here is to use the cross–entropy method
The contribution of ASPI has been to propose a multilevel splitting algorithm, in order to evaluate the probability of detection for a given configuration. When this probability is small,
these methods are known to provide a significant reduction in the variance of the relative error.
Tracking in a binary sensor network — contract with DGA / CEP (centre d'expertise parisien)
Jean–Pierre
Le Cadre
Adrien
Ickowicz
Nicolas
Ramin
See
INRIA contract ALLOC 2338 — April 2007 to October 2009.
This contract deals with surveillance of large zones via a network of video sensors. Of course, sensor outputs can be treated in a centralized architecture. However, centralized
architectures suffer from serious drawbacks. Communication constraints (e.g. bandwidth) are frequently evoked, but still more fundamentally we have to face many problems inherent of this
architecture, like:
sensor calibration, positioning and synchronization,
false alarms, multiple objects, occlusions, etc.
Overall, there is a strong need for extracting a global picture at the network level. This means that we have to focus on the level of information we can extract at the sensor level and how
to fuse them. Work has been done on the first point, using both simulated and real video sequences. The less informative level of information is the binary one. However, there is a fundamental
difference between a
{0, 1}information and
{-, + }information. A general
{0, 1}information corresponds to a detection / non–detection information. Such architecture has been widely studied in a distributed detection framework, but is
not well suited to our context. However
{0, 1}information is especially interesting if the detection process includes geographic constraints like proximity, field–of–view, etc. The
{-, + }information corresponds to a motion information: the object gets closer or is going far away. At the network level, this is a very rich information which can
present definite advantages (robustness, multi–target tracking). However, its interest depends on the network density. So, it is also necessary to consider various and complementary
decentralized architectures according to the sensing capabilities, the target behaviors and, overall, the combinatorial complexity of the problem. Work has been done for defining processings
and architectures adapted to this context.
Work has been devoted to the processing of image sequences for extracting the binary information. After considering the divergence of a local motion model, its estimation and use on real
data, we turned toward a temporal analysis of the bearing information. More precisely, bearing rates and bearing rate changes give us an estimate of the (local) target behavior. It is thus
possible to derive a local estimate of the ratio
 , through purely passive measurements, at the sensor level. Although this analysis is purely local, it performs satisfactorily on simulated sequences.
, through purely passive measurements, at the sensor level. Although this analysis is purely local, it performs satisfactorily on simulated sequences.
Concerning the information processing at the sensor level, work has been done in three directions. First, the
{-, + }informations can be summarized via the times of CPA (closest point approach) on the various sensors. A complete analysis of the target motion analysis has been
done in this framework, with various models of target motion. Then, we turned toward the analysis of the spatio–temporal
{-, + }informations. An original method based on a separation principle allows us to obtain an estimate of the target motion parameters via multiple SVM. Second, we
considered random target trajectories and target tracking. To that aim, a specific method based on multiple corrections has been developed.
Information fusion for localisation (FIL) — ANR Télécommunications
François
Le Gland
Liyun
He
See
INRIA contract ALLOC 2856 — January 2008 to December 2010.
This ANR project is coordinated by Thalès Alenia Space. Academic partners are LAAS (laboratoire d'architecture et d'analyse des systèmes), TeSA consortium including ENAC (école nationale de
l'aviation civile). Industrial partners are Microtec and Silicom.
The overall objective is to study and demonstrate information fusion algorithms for localisation of pedestrian users in an indoor environment, where GPS solution cannot be used. The sought
design combines
a pedestrian dead–reckoning (PDR) unit, providing noisy estimates of the linear displacement, angular turn, and possibly of the level change through an additional
pression sensor,
range and / or proximity measurements provided by beacons at fixed and known locations, and possibly indirect distance measurements to access points, through a
measure of the power signal attenuation,
constraints provided by an indoor map of the building (map-matching),
collaborative localisation when two users meet and exchange their respective position estimates.
Besides particle methods, which are proposed as the basic information fusion algorithm for the centralized server–based implementation, simpler algorithms such as the extended Kalman filter
(EKF) or the unscented Kalman filter (UKF) have been investigated, to be used for the local PDA–based implementation with a map of a smaller part of the building. Constraints could be taken
care of automatically with the help of a Voronoi graph
Ensemble methods for prediction and data assimilation (PREVASSEMBLE) — ANR Conception et Simulation
François
Le Gland
Sébastien
Beyou
Vu–Duc
Tran
INRIA contract ALLOC 3767 — January 2009 to December 2011.
This ANR project is coordinated by École Normale Supérieure, Paris. The other partner is Météo–France. This is a collaboration with Étienne Mémin from INRIA Rennes Bretagne Atlantique
(project–team FLUMINANCE) and with Anne Cuzol and Valérie Monbet from université de Bretagne Sud in Vannes.
The contribution of ASPI to this project is to continue the comparison
Security and reliability in digital watermarking (NEBBIANO) — ANR Sécurité
Frédéric
Cérou
Arnaud
Guyader
Cyrille
Jégourel
Fida
El Haje Hussein
See
INRIA contract ALLOC 2229 — January 2007 to December 2009.
Arnaud Guyader is coordinator of this ANR project. This is a collaboration with Teddy Furon from INRIA Rennes Bretagne Atlantique (project–team TEMICS) and Pierre Del Moral from INRIA
Bordeaux Sud–Ouest (project–team ALEA). Besides these project–teams, the other partner is LIS–INPG in Grenoble.
There are mainly two strategic axes in
[NEBBIANO]: watermarking and independent component
analysis, and watermarking and rare event simulations. To protect copyright owners, user identifiers are embedded in purchased content such as music or movie. This is basically what we mean by
watermarking. This watermarking is to be “invisible” to the standard user, and as difficult to find as possible. When content is found in an illegal place (e.g. a P2P network), the right
holders decode the hidden message, find a serial number, and thus they can trace the traitor, i.e. the client who has illegally broadcast their copy. However, the task is not that simple as
dishonest users might collude. For security reasons, anti–collusion codes have to be employed. Yet, these solutions (also called weak traceability codes) have a non–zero probability of error
defined as the probability of accusing an innocent. This probability should be, of course, extremely low, but it is also a very sensitive parameter: anti–collusion codes get longer (in terms of
the number of bits to be hidden in content) as the probability of error decreases. Fingerprint designers have to strike a trade–off, which is hard to conceive when only rough estimation of the
probability of error is known. The major issue for fingerprinting algorithms is the fact that embedding large sequences implies also assessing reliability on a huge amount of data which may be
practically unachievable without using rare event analysis. Our task within this project is to adapt our methods for estimating rare event probabilities to this framework, and provide
watermarking designers with much more accurate false detection probabilities than the bounds currently found in the literature. We have already applied these ideas to some randomized
watermarking schemes and obtained much sharper estimates of the probability of accusing an innocent.
A patent
“Validation de schémas de verrous numériques en watermarking et fingerprinting”has been submitted by INRIA and by université de Rennes 2.
Coherent detection for QPSK 40Gb systems (COHDEQ40) — ANR Télécommunications
Frédéric
Cérou
INRIA contract ALLOC 2205 — December 2006 to November 2009.
This ANR project is coordinated by Alcatel–Lucent. The other partners are Alcatel Thales III–V Lab, INT Évry, INRIA Rennes Bretagne Atlantique (project–teams ASPI and TEMICS), Kylia,
Photline and XLIM (université de Limoges).
The project COHDEQ40 intends to demonstrate the potential of coherent detection associated with digital signal processing for the next generation high density 40Gb/s WDM systems optimized
for transparency and flexibility. Key integrated optoelectronics components and specific algorithms will be developed and system evaluation performed. The INRIA task is to develop these signal
processing algorithms needed to recover the message on the decoder side. This makes full use of our knowledge of equalization and synchronization techniques involved in digital
communications.
A patent
“A decision directed algorithm for adjusting a polarization demultiplexer in a coherent detection optical receivers”has been jointly submitted in September by Alcatel Lucent and by
INRIA.
Real–time adaptive coherent heterodyne detector for future optical netowrks (TCHATER) — ANR Télécommunications
Frédéric
Cérou
INRIA contract ALLOC 2801 — January 2008 to December 2010.
This ANR project is coordinated by Alcatel–Lucent. The other partners are E2V, TELECOM ParisTech, LIP (ENS Lyon).
The primary goal of the TCHATER project is to demonstrate a coherent terminal operating at 40Gb/s using
real–timedigital signal processing and efficient polarization division multiplexing. The terminal will benefit to next-generation high information-spectral density optical networks,
while offering straightforward compatibility with current 10Gbit/s networks. It will require that advanced high–speed electronic components, especially analog–to–digital converters, are
designed within the project. Specific algorithms for polarisation demultiplexing and forward error correction with soft decoding will also have to be developed.
Slightly–multimodal transmission and detection (STRADE) — ANR Réseaux du Futur et Services
Frédéric
Cérou
INRIA contract ALLOC 4402 — November 2009 to October 2012.
This ANR project is coordinated by Alcatel–Lucent Bell Labs France. The other partners are Draka, Kylia, Université Lille 1, Institut Télécom / Télécom & Management Sud Paris
The focus of our project is to reduce the impact of nonlinear effect. The objective is twofold: specify, design, realize and evaluate fibres of reduced nonlinear effects by firstly
increasing the effective area to unprecedented values and secondly, by splitting optical power along two modes, using bimodal propagation. While the first step is ambitious but primarily relies
in the evolution of current fibre technologies, the second is disruptive and requires not only deep changes in fibre technologies but also new advanced transmitter / receiver equipment,
preferably based on coherent detection. Naturally, bimodal propagation also brings another key advantage, namely a twofold increase of system capacity.
![]() and the asymptotic variance can be estimated using an appropriate central limit theorem. To reduce the variance of the estimator, many variance reduction techniques have been proposed.
Still, running independent Monte Carlo simulations can lead to very poor results, because trajectories are generated
blindly, and only afterwards are the corresponding weights evaluated. Some of the weights can happen to be negligible, in which case the corresponding trajectories are not going to
contribute to the estimator, i.e. computing power has been wasted.
and the asymptotic variance can be estimated using an appropriate central limit theorem. To reduce the variance of the estimator, many variance reduction techniques have been proposed.
Still, running independent Monte Carlo simulations can lead to very poor results, because trajectories are generated
blindly, and only afterwards are the corresponding weights evaluated. Some of the weights can happen to be negligible, in which case the corresponding trajectories are not going to
contribute to the estimator, i.e. computing power has been wasted.![]() , with real–valued features, we want to be able to generalize, that is to guess the feature
, with real–valued features, we want to be able to generalize, that is to guess the feature
![]() , which cannot be computed by lack of knowledge of the distribution of the pair, but the Bayes estimate will help us to characterize the strength of the method. So the best we can wish
is that our estimate converges, say when the sample size grows, to the Bayes estimate. This is what has been proved in great generality by Stone
for the mean square convergence, provided that
, which cannot be computed by lack of knowledge of the distribution of the pair, but the Bayes estimate will help us to characterize the strength of the method. So the best we can wish
is that our estimate converges, say when the sample size grows, to the Bayes estimate. This is what has been proved in great generality by Stone
for the mean square convergence, provided that
![]() –continuity condition, which ensures the consistency of the estimate. Even with this recent results, the situation in infinite dimension is not completly clear, and this is still an
interesting field for investigation.
–continuity condition, which ensures the consistency of the estimate. Even with this recent results, the situation in infinite dimension is not completly clear, and this is still an
interesting field for investigation.