Scientific Foundations
Algebraic Curves and Cryptology
Though we are interested in algebraic curves by themselves, the applications to cryptology remain a motivation of our research, which is therefore especially focused on curves defined over
finite fields.
In the mid-eighties, Koblitz
More generally, for an algebraic curve over a finite field, there is a finite abelian group associated to it, called the Jacobian of the curve. Algebraic curves can be classified by their
genus; the genus of a conic is zero and elliptic curves are curves of genus 1 (in that case, the Jacobian is isomorphic to the curve). As long as the genus is not too large, the discrete
logarithm problem in the Jacobian of a curve is thought to be difficult in general, therefore one can also base cryptosystems on non-elliptic curves.
The main algorithmic tasks in relation to the use of curves in cryptography are the following:
Have an explicit description of the group and the group operation, as efficient as possible. The speed of ciphering and deciphering is indeed directly linked to the
efficiency of the group operation.
Construct curves suitable for cryptographic use: the minimal requirement for the discrete logarithm to be difficult is to have a large prime factor in the group order. It
is therefore necessary to compute the group order to check that property. This is what we call the
point counting task.
Study the security of curve-based primitives. By this, since no general framework exists to assess that security, we mean undertake an as thorough as possible study of
the security offered by those groups. The most standard way to do this is by trying to solve discrete logarithm problems in certain classes of curves.
Linear Algebra and Lattices
With “linear algebra and lattices”, we denote two classes of problems of interest: computing vectors of the kernel of a large sparse matrix defined over a finite field, and studying
algorithms to handle lattices that are given by a vector basis.
Huge linear systems are frequently encountered as last steps of “index-calculus” based algorithms for factoring or discrete logarithm computations. Those systems correspond to a particular
presentation of the underlying group by generators and relations; they are thus always defined on a base ring which is
 modulo the exponent of the group, typically
modulo the exponent of the group, typically
 in the case of factorization,
in the case of factorization,
 when trying to solve a discrete logarithm problem over
when trying to solve a discrete logarithm problem over
 . Those systems are often extremely sparse, so that specialized algorithms (Lanczós, Wiedemann) relying only on the evaluation of matrix-vector products essentially have a quadratic
complexity, instead of being cubic with the classical Gaussian elimination.
. Those systems are often extremely sparse, so that specialized algorithms (Lanczós, Wiedemann) relying only on the evaluation of matrix-vector products essentially have a quadratic
complexity, instead of being cubic with the classical Gaussian elimination.
The sizes of the matrices that are handled in record computations are such that they do not fit in the central memory of a single machine, even using a representation adapted to their sparse
nature. Some parallelism is then required, yielding various difficulties that are different from the ones encountered in the classical linear algebra problems linked to numerical analysis.
Specifically, dealing with matrices defined over finite fields precludes direct adaptation of numerical methods based on the notion of convergence and fixed-point theorems.
The second main topic is algorithmic lattice theory. Lattices are key tools in numerous problems in computer algebra, algorithmic number theory and cryptology. The typical questions one
wants to solve are to find the shortest nonzero vector in a lattice and to find the closest lattice vector to a given vector. A more general concern is to find a better lattice basis than the
one provided by the user; by “better” we mean that it consists of short, almost orthogonal vectors. This is a difficult problem in general, since finding the shortest nonzero vector is already
NP-hard, under probabilistic reductions. In 1982, Lenstra, Lenstra, and Lovász
k-BKZ reductions.
Arithmetic
We consider here the following arithmetics: integers, rational numbers, integers modulo a fixed modulus
n, finite fields, floating-point numbers and
p-adic numbers. We can divide those numbers in two classes:
exact numbers(integers, rationals, modular computations or finite fields), and
inexact numbers(floating-point and
p-adic numbers).
Algorithms on integers (respectively floating-point numbers) are very similar to those on polynomials, respectively Taylor or Laurent series. The main objective in that domain is to find new
algorithms that make operations on those numbers more efficient. These new algorithms may use an alternate number representation.
In the case of integers, we are interested in multiple-precision arithmetic. Various algorithms are to be used, depending on the sizes of the objects, starting with the most simple
“schoolbook” methods to the most advanced, asymptotically fast algorithms. The latter are often based on Fourier transforms.
The case of modular arithmetic and finite fields is the first where the representation of the elements has to be chosen carefully. Depending on the type of operations one wants to perform,
one must choose between a classical representation, the Montgomery representation, a look-up table, a polynomial representation, a normal basis representation, ... Then appropriate algorithms
must be chosen.
With
p-adic numbers, we get the first examples of non-exact representations. In that setting, one has to keep track of the precision all along a computation. The mechanisms to handle that
issue can vary: since the precision losses are not too difficult to control, one can work with a fixed global precision, or one can choose to have each element carrying its precision.
Additionally, there are several choices for representing elements, in particular when dealing with algebraic extensions of the
p-adics (ramified or unramified).
Last but not least, we are interested in the arithmetics of real numbers of floating-point type. Again, we have a notion of approximation. It is therefore necessary to decide of a
formatthat defines a set of representable numbers. Then, when the result of an arithmetical operation on two representable numbers is not representable, one should define a way to
roundit to a meaningful representable number. The purpose of the IEEE-754 standard is to give a uniform answer to these questions in order to guarantee the reliability and portability of
floating-point computations. The revised standard 754-2008 is no more restricted to the 4 basic field operations and the square root, but recommends correct rounding for some mathematical
functions, and also recommends how to extend the default available formats. This leads to efficiency questions, in particular to guarantee that the result of an operation has been correctly
rounded in arbitrary precision.
Within the context of integer arithmetic, we are also interested in putting the problem on its head, and notably by the study of the converse operation to integer
multiplication, that is, integer factoring. Being the most competitive algorithm for this task, the Number Field Sieve algorithm comes naturally as a context where several parts of our work
find a natural continuation, in all of the three axes above.
Application Domains
Cryptology
The main application domain of our project-team is cryptology. Algebraic curves have taken an increasing importance in cryptology over the last ten years. Various works have shown the
usability and the usefulness of elliptic curves in cryptology, standards (for instance, IEEE P1363
We study the suitability of higher genus curves to cryptography (mainly hyperelliptic curves of genus two, three). In particular, we work on improving the arithmetic of those curves, on the
point counting problem, and on the discrete logarithm problem.
We also have connections to cryptology through the study and development of the integer LLL algorithm, which is one of the favourite tools to cryptanalyze public-key cryptosystems. Examples
are the cryptanalysis of knapsack-based cryptosystems, the cryptanalyses of some fast variants of RSA, the cryptanalyses of fast variants of signature schemes such as DSA or Elgamal, or the
attacks against lattice based cryptosystems like NTRU. The use of floating-point arithmetic dramatically speeds up this algorithm, which renders the aforementioned cryptanalyses more
feasible.
Finally, we are studying integer factoring algorithms which are of utmost importance for the evaluation of the security of the still widely used RSA cryptosystem. In the context of our ANR
CADO grant, we are investigating the Number Field Sieve algorithm, which is the best known algorithm for factoring numbers of the kind used in practical RSA instances.
Computational Number Theory Systems
We have strong ties with several computational number theory systems, and code written by members of the project-team can be found in the Magma, Pari/GP, and Sage software tools.
Magma
[http://
magma.
maths.
usyd.
edu.
au/
magma/
]is the leading computational number theory software. It also has some features of computer algebra (algebraic geometry, polynomial system solving) but not all of what is expected of
a computer algebra system. It is developed by the team of John Cannon in Sydney.
Pari/GP
[http://
pari.
math.
u-bordeaux.
fr]is a computational number theory system which comes with a library which can be used to access Pari functions within a C program. It has originally been developed at the
Bordeaux 1 University, and is currently maintained (and expanded) by Karim Belabas, from Bordeaux University. It is free (GPL) software. We sometimes use it for validation of our
algorithms. Again, some code written by members of the project-team is incorporated into Pari.
Sage
[http://
sagemath.
org]is an open-source computer algebra system. Its development was initiated by William Stein (Univ. of Washington, Seattle). Instead of reinventing the wheel, Sage incorporates the
most efficient open-source packages in each domain, for example
Singular, Pari/GP,
Ntl,
Linbox, and the software tools
Mpfrand
Gmp-ecmdeveloped by
Cacao. Although quite new, there is already a strong community of active developers around Sage. This system is a good alternative to Maple,
Mathematica, and Magma to better disseminate our research in the future.
Arithmetics
Another indirect transfer is the usage of
Mpfrin
gfortran(since 2004), and in
Gcc, up from version 4.3 (released in 2008).
mpfris currently used at compile-time, to convert expressions like
sin(3.1416)into fixed-precision IEEE 754 formats, when the rounding mode can be statically determined. The
Mpfrlibrary is also used by the
cgallibrary for computational geometry developed by the Geometrica project-team (
InriaSophia Antipolis - Méditerranée).
The future release 4.5 of GCC will also require the
Mpclibrary; similarly to
Mpfr,
Mpcwill be used to fold at compile-time constant expressions involving complex floating-point numbers.
Software
Introduction
A major part of the research done in the
Cacaoproject-team is published within software. On the one hand, this enables everyone to check that the algorithms we develop are really efficient in
practice; on the other hand, this gives other researchers — and us of course — basic software components on which they — and we — can build other applications.
MPFR
Guillaume
Hanrot
Philippe
Théveny
Paul
Zimmermann
contact
Mpfris one of the main pieces of software developed by the
Cacaoteam. Since end 2006, with the departure of Vincent Lefèvre to
EnsLyon, it has become a joint project between
Cacaoand the
Arenaireproject-team (
InriaGrenoble - Rhône-Alpes).
Mpfris a library for computing with arbitrary precision floating-point numbers, together with well-defined semantics, and is distributed under the
Lgpllicense. In particular, all arithmetic operations are performed according to a rounding mode provided by the user, and all results are guaranteed
correct to the last bit, according to the given rounding mode.
Several software systems use
Mpfr, for example: the
Gccand
Gfortrancompilers; the
Sagecomputer algebra system; the
Kdecalculator Abakus by Michael Pyne;
cgal(Computational Geometry Algorithms Library) developed by the Geometrica project-team (
InriaSophia Antipolis - Méditerranée); Gappa, by Guillaume Melquiond; Genius Math Tool and the
Gellanguage, by Jiri Lebl; Giac/Xcas, a free computer algebra system, by Bernard Parisse; the iRRAM exact arithmetic implementation from Norbert
Müller (University of Trier, Germany); the Magma computational algebra system; and the Wcalc calculator by Kyle Wheeler.
The main developments in 2009 were: the release of version 2.4.0 (andouillette sauce moutarde) in January, with the new name GNU
Mpfr, the release of GNU
Mpfr2.4.1 in February, the CNC'2 summer school in June, and the end of the contract of Philippe Théveny in September.
All those developments were done in the context of the ODL (
Opération de Développement Logiciel) MPtools, supported by
Inriafrom September 2007 to August 2009.
MPC
Philippe
Théveny
Paul
Zimmermann
contact
Mpcis a floating-point library for complex numbers, which is developed on top of the
Mpfrlibrary, and distributed under the
Lgpllicense. It is co-written with Andreas Enge (
LFANTproject-team,
InriaBordeaux - Sud-Ouest). A complex floating-point number is represented by
x+
iy, where
xand
yare real floating-point numbers, represented using the
Mpfrlibrary. The
Mpclibrary provides correct rounding on both the real part
xand the imaginary part
yof any result.
Mpcis used in particular in the
Tripcelestial mechanics system developed at
Imcce(
Institut de Mécanique Céleste et de Calcul des Éphémérides), and by the Magma computational number theory system.
In 2009, in the context of the MPtools project, the focus was made on extending the list of available functions, to provide all functions of the C99 standard. A new version,
Mpc0.6 (Bellis perennis) was released in April,
Mpc0.7 (Campanula uniflora) was released in September, and
Mpc0.8 (Dianthus deltoides) was released in November. Since May 2009,
Mpcis used optionally by GCC 4.4 to compute constant complex expressions at compile-time (constant folding), and since December 6, 2009,
Mpcis required for the development version of GCC (thus for the next release GCC 4.5).
Gmp-
Ecm
Romain
Cosset
Pierrick
Gaudry
Alexander
Kruppa
Paul
Zimmermann
contact
Gmp-Ecmis a program to factor integers using the Elliptic Curve Method. Its efficiency comes both from the use of the
Gmplibrary, and from the implementation of state-of-the-art algorithms.
Gmp-Ecmcontains a library (
libecm) in addition to the binary program (
ecm). The binary program is distributed under
Gpl, while the library is distributed under
Lgpl, to allow its integration into other non-
Gplsoftware. For example, the Magma computational number theory software and the
Sagecomputer algebra system both use
libecm.
In 2009,
Gmp-Ecm6.2.2 and 6.2.3 have been released. In addition, the HECM implementation by Romain Cosset has been included in GMP-ECM.
Local fields
Emmanuel
Thomé
contact
Mploc is a
Clibrary for computing in
p-adic fields and their unramified extensions. The focus is mainly on
 for prime
for prime
p, and unramified extensions of
 . The ability to compute in these structures is important to several applications, such as point counting or building curves with a prescribed number of points.
. The ability to compute in these structures is important to several applications, such as point counting or building curves with a prescribed number of points.
The Mploc library is already distributed
[http://
www.
loria.
fr/
~thome/
software/
mploc]and used, although several performance improvements are sought. The library presently gathers 8,000 lines of
Csource code.
Finite fields
Pierrick
Gaudry
Emmanuel
Thomé
contact
mp is (yet another) library for computing in finite fields. The purpose of
mp
is (yet another) library for computing in finite fields. The purpose of
mp is not to provide a software layer for accessing finite fields determined at runtime within a computer algebra system like Magma, but rather to give a very efficient, optimized code for
computing in finite fields precisely known at
compile time.
mp
is not to provide a software layer for accessing finite fields determined at runtime within a computer algebra system like Magma, but rather to give a very efficient, optimized code for
computing in finite fields precisely known at
compile time.
mp is not restricted to a finite field in particular, and can adapt to finite fields of any characteristic and any extension degree. However, one of the targets being the use in cryptology,
mp
is not restricted to a finite field in particular, and can adapt to finite fields of any characteristic and any extension degree. However, one of the targets being the use in cryptology,
mp somehow focuses on prime fields and on fields of characteristic two.
somehow focuses on prime fields and on fields of characteristic two.
mp 's ability to generate specialized code for desired finite fields differentiates this library from its competitors. The performance achieved is far superior. For example,
mp
's ability to generate specialized code for desired finite fields differentiates this library from its competitors. The performance achieved is far superior. For example,
mp can be readily used to assess the throughput of an efficient software implementation of a given cryptosystem. Such an evaluation is the purpose of the “EBats” benchmarking tool
can be readily used to assess the throughput of an efficient software implementation of a given cryptosystem. Such an evaluation is the purpose of the “EBats” benchmarking tool
[http://
www.
ecrypt.
eu.
org/
ebats/
].
mp
 entered this trend in 2007, establishing reference marks for fast elliptic curve cryptography: the authors improved over the fastest examples of key-sharing software in genus 1
and 2, both over binary fields and prime fields. These timings are now comparison references for other implementations
entered this trend in 2007, establishing reference marks for fast elliptic curve cryptography: the authors improved over the fastest examples of key-sharing software in genus 1
and 2, both over binary fields and prime fields. These timings are now comparison references for other implementations
The library's purpose being the
generationof code rather than its execution, the working core of
mp
 consists of roughly 18,000 lines of Perl code, which generate most of the
Ccode. Some part of
mp
consists of roughly 18,000 lines of Perl code, which generate most of the
Ccode. Some part of
mp
 is distributed at
is distributed at
[http://
mpfq.
gforge.
inria.
fr/
].
In 2009, some experimental code for polynomials over prime fields has been added to
mp
 . Although not yet distributed it has been used for the record in genus 2 point counting (see below).
. Although not yet distributed it has been used for the record in genus 2 point counting (see below).
Polynomial arithmetic in characteristic 2
Richard
Brent
Pierrick
Gaudry
Emmanuel
Thomé
Paul
Zimmermann
contact
gf2xis a software library for polynomial multiplication over the binary field, developed together with Richard Brent (Australian National University,
Canberra, Australia). There are implementations of various algorithms corresponding to different degrees of the input polynomials. In the case of polynomials that fit into one or two
machine-words, the schoolbook algorithm has been improved and implemented using SSE instructions for maximum speed. For small degrees, we switch to Karatsuba's algorithm and then to Toom-Cook's
algorithm. These have been implemented using the most recent improvements. Finally, for very large degrees one has to switch to Fourier-transform based algorithms, namely Schönhage's or
Cantor's algorithm. In order to choose between these two asymptotically fast algorithms, we have implemented and compared them. The
gf2xpackage is distributed and maintained. It is available from
[http://
gforge.
inria.
fr/
projects/
gf2x/
]. The software library
Ntl, as of version 5.5 (April 2009) can be configured to use
gf2xas an auxiliary package for best performance.
Ntlbeing a very widespread library across the community, it is thus expected that
gf2xwill thus be used in e.g.,
Sageshortly. Documentation on the link between
Ntland
gf2xcan be obtained from
[http://
www.
shoup.
net/
ntl/
doc/
tour-gf2x.
html]. Work on
gf2xwas part of the ANC associate team (see below).
CADO-NFS
Cyril
Bouvier
Jérémie
Detrey
Pierrick
Gaudry
Alexander
Kruppa
Lionel
Muller
Emmanuel
Thomé
contact
Antonio
Vera
Paul
Zimmermann
Cado-nfsis a program to factor integers using the Number Field Sieve algorithm (NFS), developped in the context of the ANR-CADO project.
NFS is a complex algorithm which contains a large number of sub-algorithms. The implementation of all of them is now complete, but still leaves many places to be improved. Compared to
existing implementations, the
Cado-nfsimplementation is already a reasonable player. Several factorizations have been completed using our implementations.
In 2009, the linear algebra code in
Cado-nfs(which uses the block Wiedemann algorithm) has been reprogrammed mostly from scratch in
C, and now works as a multi-thread, multi-node implementation, using both POSIX threads and the MPI interface. A number of algorithms have been implemented for the basic matrix times
vector multiplications, which account for the largest share of the computation time.
During the sieving step of NFS a great number of smaller integers need to be factored. For this task an implementation of the P–1, P+1 and Elliptic Curve factoring methods has been written,
optimized for high-throughput factorization of relatively small numbers (unlike GMP-ECM, which uses asymptotically fast algorithms to find factors as large as possible with these algorithms).
The code is competitive in terms of performance/cost-ratio with recently proposed hardware implementations of ECM for NFS. The details of the implementation are published in the research report
In 2009, the
Cado-nfsprogram has been made available publicly from
[http://
cado-nfs.
gforge.
inria.
fr/
]. New versions of programs for the filtering step have been designed — with the help of Cyril Bouvier — for the factorization of RSA-768; those programs will be integrated
within
Cado-nfsby Lionel Muller.
New Results
Floating-Point Arithmetic
Guillaume
Hanrot
Philippe
Théveny
Paul
Zimmermann
Together with Siegfried Rump, Sylvie Boldo and Guillaume Melquiond, P. Zimmermann published a new efficient algorithm to compute the predecessor or successor of a floating-point number
in rounding to nearest mode
With Vincent Lefèvre from the Arenaire project-team, and Kaveh Ghazi (GCC developer), Ph. Théveny and P. Zimmermann submitted an article entitled
Why and how to use arbitrary precisionto the journal
Computing in Science and Engineering.
Exact arithmetic
Pierrick
Gaudry
Guillaume
Hanrot
Alexander
Kruppa
Emmanuel
Thomé
Paul
Zimmermann
Richard Brent and P. Zimmermann are collaborating on a book called “Modern Computer Arithmetic”. Three new versions (0.2.1 in March, 0.3 in June, and 0.4 in November) have been
published in 2009, in the context of the
InriaANC associate team
[http://
www.
loria.
fr/
~zimmerma/
anc.
html]which started in 2008. Version 0.4 includes feedback from two anonymous reviewers for a commercial publisher.
Another common project with Richard Brent is the search for primitive trinomials over
 . While the paper corresponding to degrees 24036583, 25964951, 30402457, and 32582657 appeared
. While the paper corresponding to degrees 24036583, 25964951, 30402457, and 32582657 appeared
x43112609+
x3569337+ 1,
x43112609+
x4463337+ 1,
x43112609+
x17212521+ 1,
x43112609+
x21078848+ 1,
and for degree
r= 42643801, we have found exactly five:
xr+
x55981+ 1,
xr+
x3706066+ 1,
xr+
x3896488+ 1,
xr+
x12899278+ 1,
xr+
x20150445+ 1.
All those primitive trinomials have been checked by Allan Steel using Magma. Those results will be published in an invited paper to the AMS Notices.
Together with Will Orrick (Indiana University) and Judy-anne Osborn (Australian National University), Richard Brent and P. Zimmermann started another project on maximal determinants of
Hadamard matrices. Results so far include the fact that the conjectured maximal determinant for
n= 19is the true maximal determinant, and similarly for
n= 37. This work was done with the support of the ANC associate team too.
Together with Philippe Dumas, Claude Gomez and Bruno Salvy, P. Zimmermann published an electronic version of the book “Calcul formel : mode d'emploi. Exemples en Maple” (in french),
previously published by a commercial editor, and whose rights have been given back to the authors
Curve-related results
Răzvan
Bărbulescu
Gaëtan
Bisson
Iram
Chelli
Romain
Cosset
Pierrick
Gaudry
Guillaume
Hanrot
Damien
Robert
Emmanuel
Thomé
Over the winter, Gaëtan Bisson has been working jointly with Andrew V. Sutherland (Massachusetts Institute of Technology) on new algorithms for computing endomorphism rings of ordinary
elliptic curves over finite fields
During his master project internship, Iram Chelli has designed a fully deterministic ECM algorithm
B1= 260and
B2= 11600enable one to find all prime factors up to
2
32in any composite integer.
Răzvan Bărbulescu has found two infinite sub-families of Suyama curves for which the probability to give a factorization is higher
Romain Cosset has worked on developing a genus-2 “hyperelliptic curve method” for integer factoring
Damien Robert and David Lubicz have worked on explicit isogeny computation in genus 2. With Jean-Charles Faugère, they have defined a modular correspondance between abelian varieties
Pierrick Gaudry and Éric Schost finished a record-setting computation of a so-called doubly-secure genus 2 curve for cryptographic use. The computation is based on their previous
experiment of Spring 2008, where a single curve was computed. The software has been improved – some critical parts now use the
mp
 library – and has been run on thousands of curves until one with good cryptographic properties was obtained. They used the Sharcnet grid facility
library – and has been run on thousands of curves until one with good cryptographic properties was obtained. They used the Sharcnet grid facility
[http://
www.
sharcnet.
ca], on which they obtained a “Dedicated Ressource” grant of one and a half million hours. This result has been announced in oral communications at conferences, and a journal paper is
under writing.
Andreas Enge, Pierrick Gaudry and Emmanuel Thomé have finished their common article describing a class of curves for which they give a discrete logarithm algorithm with heuristic complexity
Lqg(1/3), where
gis the genus and
qthe cardinality of the finite field. The article has been accepted to Journal of Cryptology
The article
Number Field Sieve-related results
Pierrick
Gaudry
Alexander
Kruppa
Emmanuel
Thomé
Paul
Zimmermann
The team has been involved in the factorization of RSA-768, a 768-bit integer. With the usage of Grid'5000 computers in “besteffort” mode, we have obtained more than 40% of a total of 64
billion relations in the first phase (sieving). Some experiments were done together with an internship, Cyril Bouvier, for the filtering phase. The linear algebra phase is expected to finish by
the end of 2009, or at the turn of the year. The linear algebra phase is considerably more challenging than the sieving phase in terms of program distribution. The block Wiedemann algorithm,
which is being used for this computation, makes it possible to distribute the computation somewhat. Using Grid'5000 computers, we have been able to participate to a large extent to the linear
algebra computation. The work on RSA-768 is expected to yield several forthcoming papers describing the many facets of the experiment.
Antoine Joux, Reynald Lercier, David Naccache and Emmanuel Thomé extended their work on oracle-assisted modular
e-th root computation to an attack on the so-called static Diffie-Hellmann problem
Hardware accelerators for pairing-based cryptography
Jérémie
Detrey
Nicolas
Estibals
Together with J.-L. Beuchat, E. Okamoto (LCIS, University of Tsukuba, Japan), and F. Rodríguez-Henríquez (CINVESTAV, IPN, Mexico), J. Detrey and N. Estibals have
proposed a new family of dedicated hardware coprocessors for computing the Tate pairing over supersingular elliptic curves in characteristic three. Designed following a performance-oriented
rationale and based upon a fully parallel Karatsuba-like multiplier, these accelerators achieve the fastest computation speeds in the open literature (for instance, under
17
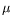 s for 109 bits of equivalent symmetric-key security). Moreover, due to a carefully
controlled adequation between arithmetic, algorithms and architecture, these coprocessors also yield the best publicly-known area–time tradeoffs.
s for 109 bits of equivalent symmetric-key security). Moreover, due to a carefully
controlled adequation between arithmetic, algorithms and architecture, these coprocessors also yield the best publicly-known area–time tradeoffs.
This work was published at the CHES 2009 conference
N. Estibals has also developed a flexible compiler for a wide family of generic finite-field arithmetic coprocessors during his Master project
Symmetric cryptography
Marion
Videau
In October 2008, Marion Videau together with all the other 13 co-authors of the proposition submitted a new proposition called Shabal
In September 2009, a common work with Andrea Röck (Helsinki University of Technology) and Vincent Strubel (ANSSI) on the Linux kernel random generator has been presented at
Journées C2in Fréjus.
Legal aspects and security
Marion
Videau
In May 2009, Marion Videau made a presentation entitled “Aspects techniques de la preuve reposant sur l'écrit électronique” on the occasion of a symposium “La preuve des actes juridiques
électroniques privés : mosaïque des droits européens ou trait d'Union”, organized by the “Centre René DEMOGUE” of the “Faculté des Sciences Juridiques, Politiques et Sociales” of the University
Lille 2. An article corresponding to its presentation has been published in
In July 2009, Marion Videau also made a presentation and a poster entitled “Preliminary thoughts on national health identifier systems” on the occasion of the Young Engineering Scientist
Symposium 2009 organized by the Office for Science and Technology (Ambassy of France, Washington DC).
Other results
S. Burckel, E. Gioan and E. Thomé wrote a paper on the computation of multi-dimensional mappings using a minimal number of intermediary registers. This paper has been presented at the UC
2009 conference
Dissemination
Scientific Animation
Cacaoseminar
We have a seminar, where we have invited in 2009 the following speakers: Jean-Luc Beuchat, Nicolas Guillermin, Andy Novocin, Judy-Anne Osborn, Tadanori Teruya, Shi Bai, and Éric Brier.
Conference organization
Pierrick Gaudry and Emmanuel Thomé, together with Anne-Lise Charbonnier from the “comité colloques” of INRIA Nancy - Grand Est, are organizing the ANTS-IX conference
[http://
www.
ants9.
org/
], to be held at LORIA in July 2010. In 2009, the main part has been to search for sponsors and grants in order to prepare a budget. Jérémie Detrey designed the poster.
Committees memberships
P. Gaudry was a member in the “Comité de Sélection” for the hiring of an assistant Professor in Bordeaux (section 25). He was referee for the PhD thesis of Cédric Faure (École
polytechnique and INRIA). He was a PC member of the PAIRING 2009 conference (Stanford, USA, August 2009) and of the INDOCRYPT 2009 conference (to be held in New Dehli, INDIA, December
2009).
M. Videau was a member of the program committee of the WCC'09 conference, which took place in Ullensvang (Norway) in May 2009. She was also a member of the program committee of the
SSTIC'09 conference, which took place in Rennes (France) in June 2009.
P. Zimmermann is member of the program committee of the Arith'19 conference, which took place in Portland (Oregon) in June 2009. He was head in 2009 of the INRIA hiring committee for
CR1 and CR2 at INRIA Nancy - Grand Est. He is also head of the “comité colloques” of INRIA Nancy - Grand Est, member of the “comité de liaison” of the new thematic group MAIRCI of the SMAI
(Société de Mathématiques Appliquées et Industrielles), and was member of the PhD thesis committee of Guillaume Revy (ENS Lyon).
Vulgarization
J. Detrey and P. Zimmermann participated once and twice, respectively, to the “
Une journée avec un scientifique” program, where high-school students are invited to discover scientific research by spending a day among researchers, during which they are shown the
various aspects of the job.
P. Gaudry wrote an article about curves and cryptography, to be published, early 2010 in
Pour la science.
Invited Conferences
P. Gaudry gave two one-hour invited talks at the “9th Central European Conference on Cryptography” in Třebíč, Czech Republic, and for the colloquium in the honor of Gerhard Frey for his
retirement in Essen, Germany. He will give a 40-minute invited talk at the “Théorie des nombres et Applications” workshop, to be held at the CIRM center, Luminy, France, in December.
P. Zimmermann gave an invited talk at the 2nd public workshop of the SCIEnce Project in January (Paris, France), another one at Microsoft Research in June (Redmond, USA), and a third
one at the
Rencontres “Arithmétique de l'Informatique Mathématique”(RAIM'09) in October (Lyon, France).
E. Thomé gave an invited talk at the Sage Days 16 workshop in Barcelone (June).
J. Detrey gave an invited talk at the
Rencontres “Arithmétique de l'Informatique Mathématique”(RAIM'09) in October (Lyon, France).
Teaching
J. Detrey and G. Hanrot gave eight and twelve hours of lectures, respectively, at the
Master d'Informatique Fondamentaleof ENS Lyon, on the topic of elliptic curves and pairings applied to cryptography. They also sat in the examination jury for this course.
J. Detrey gave a two-hour lecture in
licence professionnelleat IUT Charlemagne (Nancy) on the topic of security.
E. Thomé gave 8 hours of Master 1 courses at Université Henri Poincaré on the topic of cryptology and computer networks.
E. Thomé is a member of the jury of the competitive exam for the École polytechnique.
J. Detrey gave a twelve-hour course on the topic of pairings and pairing-based cryptography, as part of the Master in Computer Science of the CINVESTAV (Mexico
City).
P. Gaudry gave 30 hours of Master 1 courses at Université Henri Poincaré on the topic of cryptology.
P. Gaudry and G. Hanrot are members of the jury of “agrégation externe de mathématiques”, a competitive exam to hire high school teachers.
J. Detrey supervised the Master 2 internship of Nicolas Estibals (ENS Lyon) on the topic of automatic compilation of arithmetic algorithms on families of
finite-field coprocessors.
P. Gaudry supervised the Master 1 internship of Răzvan Bărbulescu (ENS Lyon) on the topic of integer factorization using elliptic curves.
P. Zimmermann supervised the Master 2 internship of Iram Chelli (Univ. Limoges) on the topic of a deterministic elliptic curve method.
J. Detrey gave a three-hour lecture at the
Centre de formation à la sécurité des systèmes d'informationon the topic of discrete logarithm and elliptic curves.
M. Videau gave 36 hours of lectures at the
Centre de formation à la sécurité des systèmes d'informationon cryptography.
M. Videau gave 12 hours of lectures in cryptography at École Supérieure d'Informatique et Applications de Lorraine.
M. Videau gave 26 hours of tutorials in algorithmic and programming at École Nationale Supérieure de Techniques Avancées.
M. Videau gave a 2 hours seminar course on technical aspects of electronic proofs at the
Master Professionnel M2 - Spécialité Droit du Commerce Électronique et de l'Économie Numériqueof the University Paris I.
![]() , for various
, for various