Mathematical and numerical analysis
Nicolas
Besse
Mihai
Bostan
Nicolas
Crouseilles
Sever
Hirstoaga
Simon
Labrunie
Sandrine
Marchal
Thomas
Respaud
Jean
Roche
Eric
Sonnendrücker
We have established several existence and uniqueness results for collisionless kinetic models, the Vlasov-Poisson and Vlasov-Maxwell equations of plasma physics but also the Nordström-Vlasov
equations used in astrophysics. We also investigated different asymptotic regimes for the Vlasov-Maxwell equations. Finally, this section includes recent results concerning the convergence of
the numerical solution towards the solution of the model (Maxwell or Vlasov).
Asymptotic regimes and existence results for the Vlasov-Poisson and Vlasov-Maxwell equations
In
t>0. More precisely, for each
xthe support of the density is assumed to be an interval
[
p
-,
p
+]with end-points varying in space and time. We analyze here the case of weak and strong solutions for the effective equations verified by the end-points and the electric
field (water-bag model) in the relativistic setting.
We study the existence of weak solutions for the stationary Nordström-Vlasov equations in a bounded domain. The proof follows by fixed point method. The asymptotic behavior for large light
speed is analyzed as well. We justify the convergence towards the stationary Vlasov-Poisson model for stellar dynamics
The subject matter of
We investigate the well posedness of stationary Vlasov-Boltzmann equations both in the simpler case of linear problems with a space varying force field, and, the non-linear
Vlasov-Poisson-Boltzmann system. For the former we obtain existence-uniqueness results for arbitrarily large integrable boundary data and justify further a priori estimates. For the later the
boundary data needs to satisfy an entropy condition guaranteeing classical statistical equilibrium at the boundary. This stationary problem relates to the existence of phase transitions
associated with slab geometries
The subject matter of
One of the main applications in plasma physics is the energy production through thermo-nuclear fusion. Magnetic confinement controlled fusion requires the confinement of the plasma within
a bounded domain using a strong magnetic field. Several models exist for describing the evolution of strongly magnetized plasmas. In
On the other hand, in order to derive a drift-kinetic model, we consider in
We consider the equation
H(
Du) =
H(0),
x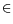
RN. More precisely we investigate under which hypotheses the constant functions are the only bounded solutions. In arbitrary space dimension we prove that this happens when
convexity and coercivity occur. In one space dimension we show that the above property holds true for Hamiltonians in a larger class. These results apply when studying the long time behaviour
of solutions for time-dependent Hamilton-Jacobi equations
We began

where
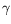 is a given function,
is a given function,
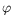 is the potential created by the particles,
is the potential created by the particles,
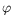
eis an external potential,
Mis the total mass of the particles, and
 is adjusted to satisfy the mass constraint. The qualitative properties of the solution have been established, with an emphasis on the behaviour of the potential
is adjusted to satisfy the mass constraint. The qualitative properties of the solution have been established, with an emphasis on the behaviour of the potential
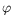 and the density
and the density
 in the neighbourhood of the re-entrant corner. Asymptotics (as a function of the total mass
in the neighbourhood of the re-entrant corner. Asymptotics (as a function of the total mass
M) have been obtained in the case of a Maxwellian distribution, i.e. when
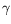 (
(
s) = exp(-
s). This is the first step towards the analysis of singularities of the time-dependent Vlasov–Poisson and Vlasov–Maxwell systems, though considerable difficulties
have to be overcome.
We studied in
Convergence studies of numerical methods
The subject matter of
In the paper
On a different topic, we analysed numerically the so-called Fourier–Singular Complement Method for the time-dependent Maxwell equations in an axisymmetric domain
Domain decomposition for the solution of nonlinear equations
This is a joint work with Noureddine Alaa, Professor at the Marrakech Cadi Ayyad University. Strongly degenerate parabolic problems have received considerable attentions, and various forms
of this problems have been proposed in the literature, especially in the area of reaction-diffusion equations with cross-diffusion, such problems arise from biological, chemical and physical
systems. Various methods have been proposed in the mathematical literature to study the existence, uniqueness and compute numerical approximation of solutions for quasi-linear partial
differential equation problems.
In this work we give a result of existence of weak solutions for some quasi-linear parabolic and periodic problem and present a method to compute a numerical solution. The algorithm is
based on the Schwarz overlapping domain decomposition method, combined with finite element method. In a first step a super-solution is computed. In a second step a weak solution of the
nonlinear problem is computed using a Newton method, see
Mathematical study of water-bag models
The multi-water-bag representation of the statistical distribution function of particles can be viewed as a special class of exact weak solution of the Vlasov equation, allowing to reduce
this latter into a set of hydrodynamic equations while keeping its kinetic character. Therefore finding water-bag-like weak solutions of the gyrokinetic equations leads to the birth of the
gyro-water-bag model.
The paper
In
In
Development of Vlasov solvers
Nicolas
Besse
Martin
Campos Pinto
Nicolas
Crouseilles
Alain
Ghizzo
Michaël
Gutnic
Matthieu
Haefelé
Olivier
Hoenen
Sébastien
Jund
Guillaume
Latu
Michel
Mehrenberger
Thomas
Respaud
Stéphanie
Salmon
Eric
Sonnendrücker
Two-dimensional solvers
In
Another strategy based on conservative semi-Lagrangian methods has been implemented and tested. Whereas semi-Lagrangian methods compute the distribution function on the grid points,
conservative methods considers an average of the unknown on each cell. This approximation enables the solving of multi-dimensional problems by a successive solving of one-dimensional
equations. This work started last year and has been achieved this year (see
A 2D version of LOSS that uses GPGPU computing units has been designed. On a personal computer, we obtain speedups up to 80 using the GPU versus the conventional processor. The domain
decomposition strategy is the same as in our previous MPI version of LOSS. Porting codes on GPGPU is cost-effective, because high speedups could be achieved on a low-cost machine. But it is
also time-consuming for the developer.
The conservative scheme PFC (developed in
CALVI platform
The aim of the platform is to change the way numerical methods are implemented and tested. It has been initiated because most of the researchers of the CALVI project develop new numerical
methods for almost the same equations. Until now, every researchers implemented their methods as stand-alone C or Fortran applications. So, each researcher, for each code, has to implement
the validation process by himself without using previous implementation done by himself or another member of the project. The platform move the implementation from stand-alone application to
a module oriented one. Thanks to standardized application programing interfaces (API), the different numerical methods can be swapped between them and can be validated within a common
skeleton. This common skeleton plus the standard API is actually the platform. A better reuse of existing modules is expected as well as an increased efficiency in numerical methods
implementation.
The whole implementation has been refactored this year according to remarks made by the team. So the python package called 'vlasy', which stands for 'Vlasov' + 'Python', is born. Lot's of
things that were accessible to the user are now embedded in Python classes within the package. As a result, the user access objects at higher level of abstraction, thus making the usage
easier. Some unit tests have been introduced in the skeleton part of the package and solver validation process is also implemented as unit tests. Two Vlasov solvers have been added as well as
4 test cases. The vlasy package is already used at CEA Cadarache in a physics team.
Four-dimensional solvers
A four-dimensional cubic splines interpolation has been validated in the framework of the backward semi-Lagrangian method on the Vlasov-Poisson equations. This study was motivated to study
the validity of the time splitting of the method when non-conservative advection terms are involved. The method is currently tested on more complex problems and appears to be competitive from
a CPU time point of view. This approach benefits from the Local Splines strategy which enables a decomposition domain well suited for parallel implementation. This non split scheme has been
recently added in the Gysela code. It provides a reference numerical scheme that avoids some approximations that come with splitting. Furthermore, it will allow in the future for alternative
and more accurate ways to track the feet of the characteristics.
Adaptive solvers
In
The present scheme implements similar ideas, but now in the framework of interpolatory wavelets. For this purpose we translate the property of being (strongly) well-adapted to a given
function in the context of wavelet trees, and show that it is (weakly) preserved by a low-cost prediction algorithm which transports wavelet grids along any smooth flow. As a consequence,
error estimates can be established for the resulting “predict and readapt” scheme under the essential assumption that the flow underlying the transport equation, as well as its numerical
approximation, is a stable diffeomorphism. One complexity result is stated in addition.
Electromagnetic Particle In Cell (PIC) solvers
This project funded by ANR proposes to develop and compare Finite Element Time Domain (FETD) solvers based on the one hand on high order H(curl) conforming elements and on the other hand
on high order Discontinuous Galerkin (DG) finite elements and investigate their coupling to the particles. These self consistent relativistic PIC solvers will be the first of this kind in
this context and promise to have an impact for the simulation of realistic problems in accelerator and plasma physics.
During the last year we further developed a previous work on charge conserving Finite Element PIC schemes on general grids
A parallel code (Spin) has been developed to solve bigger test cases using the same numerical method. Spin solves Maxwell equations on hybrid meshes in 2D space (quadrangles and triangles)
using edge finite elements. A Poisson solver, that uses also edge finite elements, is called once at the beginning of each run to find the initial self-consistent electric field. The work
distribution on processors is well balanced on several dozens of cores in this 2D version. The 3D version of Spin is currently under development.
Multiple time scales solvers and Magneto HydroDynamics
Jean-Philippe
Braeunig
Emmanuel
Frénod
Michaël
Gutnic
Philippe
Helluy
Alexandre
Mouton
Eric
Sonnendrücker
Multiple time scales solvers
One of the most important difficulties of numerical simulation of magnetized plasmas is the existence of multiple time and space scales, which can be very different. In order to produce
good simulations of these multiscale phenomena, we have investigated the development of models and numerical methods which are adapted to these problems. The two-scale convergence theory
introduced by G. Nguetseng and G. Allaire is one of the tools which can be used to rigorously derive multiscale limits and to obtain new limit models which can be discretized with a usual
numerical method: we call this procedure a two-scale numerical method. Within the thesis of Alexandre Mouton we developed a two-scale semi-Lagrangian method and applied it on a gyrokinetic
Vlasov-like model in order to simulate a plasma submitted to a large external magnetic field. In order to tackle this complex model, we first investigated this idea in simpler cases. First,
we developed a two-scale finite volume method applied to the weakly compressible 1D isentropic Euler equations. Even if this mathematical context is far from a Vlasov-like model, it is a
relatively simple framework in order to study the behaviour of a two-scale numerical method in front of a nonlinear model. In a second part, we developed a two-scale semi-Lagrangian method
for the two-scale model developed by E. Frénod, F. Salvarani et E. Sonnendrücker in order to simulate axisymmetric charged particle beams. Even if the studied physical phenomena are quite
different from magnetic fusion experiments, the mathematical context of the one-dimensional paraxial Vlasov-Poisson model is very simple for establishing the basis of a two-scale
semi-Lagrangian method. Finally, we used the two-scale convergence theory in order to improve M. Bostan's weak-* convergence results about the finite Larmor radius model, and we developed a
forward semi-Lagrangian method implementing the two-scale method.
Magneto HydroDynamics
The MagnetoHydroDynamics (MHD) equations are a simplified but rich model of conducting fluids. They can be used in some parts of ITER but also in stellar physics, geophysics and plasmas
physics. The Discontinuous Galerkin (DG) method is already used for solving MHD problems. It has proved to be very efficient and accurate. However, several difficulties are still present:
-in some cases, the MHD first order equations admit several entropy solutions. The DG method can be designed in order to satisfy an entropy principle, but it is not clear
how it behaves in case of multiple solutions;
-if in some parts of the mesh small cells are required, it is important, for efficiency reasons to be able to deal with several time step sizes;
-finally, the divergence free condition is treated by the hyperbolic divergence cleaning technique (see references in
As a conclusion, this project permitted to address relevant problems in the approximation of the MHD equations by DG schemes. The scheme has been implemented in CM2, a parallel and general
purpose CFD code.
Numerical simulation of compressible multi-material fluid flows
Participant:Jean-Philippe Braeunig
This work is achieved in collaboration with J.-M. Ghidaglia (ENS Cachan), F. Dias (ENS cachan) and B. Desjardins (ENS Ulm) in the frame of the Laboratoire de Recherche
Commun MESO (ENS cachan - CEA Bruyères-le-Châtel).
This collaboration has begun during Braeunig's PhD (2004-2007) which was a collaboration CEA-ENS Cachan. We have designed a novel pure eulerian Finite Volumes method for
compressible multi-material fluid flows with sharp interface capturing called FVCF-NIP, (Finite Volumes with Characteristic Flux (VFFC) scheme of Ghidaglia et al, interface capturing Natural
Interface Positioning (NIP)). A new concept is introduced, the condensate, which allows to handle mixed cells containing two or more materials and to calculate the evolution of the interface
on the fixed eulerian grid. The main features of this method are: second order in time and space, local conservation of mass, momentum and total energy, no diffusion of any materials eulerian
quantity on each others through the interface and free sliding of materials on each others at the interface. This work is described in Braeunig's PhD report 2007 and in a paper by Braeunig et
al
This method is used for industrial applications. One of them is the simulation of Liquefied Natural Gas (LNG) sloshing in LNG carriers (LNG tanks in a boat). The issue was
to study and design a procedure to extrapolate experimental results obtained in laboratory with a small scale model (scale 1/40) to the scale of the LNG carrier (scale 1) taking into account
compressible effects. A scaling law has been proposed and validated numerically with a VFFC-NIP code. The code has been validated by comparing results with analytical solutions and with a
reduced numerical model on academic benchmarks. This work has been presented by J.-M. Ghidaglia at ISOPE 2010 Conference and described in a paper in the ISOPE 2010 Conference Proceeding, see
Braeunig et al
Application of Vlasov codes to magnetic fusion
Pierre
Bertrand
Nicolas
Besse
Jean-Philippe
Braeunig
Nicolas
Crouseilles
Daniele
Del Sarto
Sever
Hirstoaga
Giovanni
Manfredi
Michel
Mehrenberger
Etienne
Gravier
Guillaume
Latu
Jean
Roche
Amar
Mokrani
Simon
Labrunie
Hocine
Sellama
Eric
Sonnendrücker
The computation of turbulent thermal diffusivities in fusion plasmas is of prime importance since the energy confinement is determined by these transport coefficients. Fusion plasmas are
thus prompt to instabilities and required a self-consistent analysis of the plasmas and the electromagnetic fields. Since collisions between particles play a negligible role, the kinetic plasma
behavior is described by the well-known Vlasov model. A key issue is the resonant interaction between particles and waves, which has to be accurately described. The self consistent coupling of
the electromagnetic fields then exhibits resonant (Landau) interactions between charged particles and electromagnetic waves, a feature that cannot be addressed in the fluid limit.
Development of a 5D gyrokinetic code
The collaboration around the optimization of the GYSELA code used for gyrokinetic simulations of turbulence in tokamaks went on. The upgrade from four to five dimensions of the phase space
is now efficient on several thousands of processors. Last year, several developments of the code enabled to achieve this task.
The aim of this work is to improve the accuracy and the physical relevance of the GYSELA 5D code. Mainly, we would like to perform simulations using a mesh based on curvilinear coordinates
in such a way mesh lines are aligned with magnetic field lines. This will diminish numerical diffusion, reduce the size of the computations and improve results accuracy. Moreover, a
conservative scheme for plasma turbulence simulations will be used. Using a conservative formalism is an asset for physical relevance of simulations and allows a directional splitting of the
Vlasov equation, what is very convenient to deal with curvilinear meshes.
We started in this way by studying conservative numerical methods with curvilinear coordinates for the Guiding-Center (GC) model, which is a reduced 2D conservative model
for plasma turbulence. We use the Parabolic Spline Method (PSM), which is a semi-lagrangian conservative scheme using a cubic spline reconstruction. It is a similar method to the Backward
Semi-Lagrangian (BSL) scheme
Afterward, the conservative semi-lagrangian PSM scheme has been integrated in the GYSELA code. We first have faced numerical difficulties about the velocity field
characteristics. We noticed that cells geometric evolution through the scheme should conserve their volumes, what is equivalent to have a divergence free velocity field at the discrete level,
and not only at the continuous level. It is important to obtain a robust scheme in the sense of getting nearby a maximum principle condition. In the same way of improving robustness, we
propose an "entropic flux limiter" for the PSM scheme to cut off the spurious oscillations that may appear when dealing with small scales turbulent structures in the flow, below the mesh
size. A different way of MPI parallel computing is used for this scheme (transposition), achieved by Guillaume Latu. Drift kinetic
4
Dbenchmarks have been performed and compared with the former BSL scheme. This work is described in an INRIA report Braeunig et al
Physicists have improved the Gysela code in order to add heat flux driven ion turbulence. It involves large displacements during the advection phase of the Semi-Lagrangian method. In order
to take care of this new feature, another parallel algorithm is needed to replace the
local spline methodthat requires a too strong CFL-like condition. A 4D transposition parallel operator has been found that provides a solution. Even if the communication time is
growing with this new algorithm, it remains less than the advection computing time, even for big runs. The overall parallel relative efficiency of Gysela decreased in this new configuration,
nevertheless the asymptotic behaviour (for large number of processors) is still very scalable.
Numerical study of the gyroaverage operator
In this work, we are concerned with numerical approximation of the gyroaverage operators arising in plasma physics to take into account the effects of the finite Larmor radius corrections.
Several methods are proposed in the space configuration and compared to the reference spectral method. In particular, a new method is proposed; the basic point is the expansion of the
function on a basis (such as polynomial basis). Computing the gyroaverage of a function then reduces to compute the gyroaverage of its basis, which are known analytically. Hence, in the same
way as finite element formulation, the method can be formulated into a matrix form. The approach presents other several advantages. On the one side, the number of quadrature points is
automatically determined as the intersection between the mesh and the Larmor circle, which provides the necessary adaptivity to reach a good accuracy even for large Larmor circles. Contrary
to previous works, the basis function are not evaluated at the quadrature points but integrated on a circle arc, which turns out to be more accurate. the gyroaverage operator also includes an
integration with respect to the Larmor radius which belongs to
[0, +
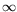 ]. Hence a good accuracy when large Larmor radius are considered is required.
But, it turns out that it is not sufficient since the numerical integration with respect to the Larmor radius is also important in order to reach a good accuracy for the gyroaverage operator.
For example, traditional quadrature rules (such as trapezoidal or Laguerre ones) are not sufficiently efficient. In this context, we develop a new approach which appears to be very efficient
for arbitrary wave numbers. The coupling with the guiding-center model leads to very good results compared to the analytical results in the linear regime and to the spectral method for the
gyroaverage operator. We then investigate the influence of the different approximations considering the coupling with some guiding-center models available in the literature.
]. Hence a good accuracy when large Larmor radius are considered is required.
But, it turns out that it is not sufficient since the numerical integration with respect to the Larmor radius is also important in order to reach a good accuracy for the gyroaverage operator.
For example, traditional quadrature rules (such as trapezoidal or Laguerre ones) are not sufficiently efficient. In this context, we develop a new approach which appears to be very efficient
for arbitrary wave numbers. The coupling with the guiding-center model leads to very good results compared to the analytical results in the linear regime and to the spectral method for the
gyroaverage operator. We then investigate the influence of the different approximations considering the coupling with some guiding-center models available in the literature.
Plasma-wall interactions – application to ELM modes on JET
The vast majority of plasmas produced in the laboratory are in contact with a material surface. In fusion devices, the surface can be either the material vessel that contains the plasma,
or some
ad-hocdevice (limiter or divertor) specifically designed to optimize the interaction with the charged particles. These surfaces are eroded by ion and neutral bombardment and may thus
see their lifetime considerably reduced. This is one of the key issues for the ITER tokamak, and even more so, for future commercial power plants.
The heat load on the divertor plates can be considerably strained during violent events known as ELMs (edge-localized modes). Although the precise origin of ELMs is still under debate, in
practice, these events result in the ejection of energetic charged particles beyond the magnetic separatrix. These particles travel along the magnetic field lines and end up hitting the
divertor plates.
In order to model such a scenario, we have developed a 1D Vlasov-Poisson code with open boundaries, for both ions and electrons. The spatial co-ordinate represents the distance along the
magnetic field line, whereas the absorbing boundaries are supposed to mimic the divertor plates. Appropriate diagnostics are set up to compute the particles and heat fluxes on the plates.
The main numerical bottleneck is represented by the very large ratio between the system size (
 m) and the Debye length (
m) and the Debye length (
 m). A possible approach is to use the recently developed “asymptotic preserving” schemes
m). A possible approach is to use the recently developed “asymptotic preserving” schemes
Gyro-water-bag approach
In the Gyro-Water-Bag (GWB) approach, a discrete distribution function taking the form of a multi-step like function is used in place of the continuous distribution function along the
velocity direction. According to Liouville's phase-space conservation property the distribution function remains constant in time between the bag contours. The time evolution of the system is
completely described by the knowledge of the contours. We get a set of hydrodynamic equations, where the system behaves as
Nfluids coupled together by the electromagnetic fields (in our case the quasi-neutrality). As a matter of fact a small bag number (not more than 10) has been shown to be sufficient to
correctly describe the Ion Temperature Gradient (ITG) instability observed in fusion plasmas. Thus the water-bag offers an exact description of the plasma dynamics even with a small bag
number, allowing more analytical studies and bringing the link between the hydrodynamic description and the full Vlasov one. Encouraging results have been obtained using three nonlinear
waterbag codes: a 3D nonlinear self-consistent gyro-water-bag code which is based on a semi-Lagrangian method (this code was subject to comparison with the GYSELA code dealing with
curvilinear meshes); a 3D quasilinear self-consistent gyro-water-bag code and a 1D nonlinear self-consistent electromagnetic-water-bag code where the Discontinuous Galerkin methods are
used.
Trapped-ion driven turbulence: gyrokinetic modeling
Drift wave instabilities and their subsequent turbulence are believed to be an important component of the experimentally observed anomalous transport of heat in tokamaks. It was known for
several decades, that the transport is “anomalous” in the sense that it does not follow the standard magnitude scaling of collisional transport. Expressed in terms of diffusivities the
transport of ions and electrons is comparable, in the range of one or fewer times
1
m
2
s
-1in the core region, which is indeed one order of magnitude larger than the collisional ion transport and three higher than collisional electron transport.
Most previous studies of ion-temperature-gradient-driven drift wave turbulence have utilized a simple one-field, nonlinear fluid model, known as the Hasegawa-Mima (HM) equation. This
equation is an important paradigm for the description of drift-wave turbulence in magnetically confined plasmas and has a structure similar to that of the Charney equation, describing
geostrophic motions in planetary atmospheres. This model is indeed connected to two-dimensional (2D) turbulence. However it is well known that, for 2D turbulence, the feature of turbulence
are different from the standard 3D turbulence.
At this step, different remarks must be pointed out:
(i) At high temperature and taking into account the toroidal effects, collisionless kinetic effects allow an effective short time decoupling of particles and field lines (“defreezing
effects”) thereby introducing non fluid effects, as Landau resonances, strong finite Larmor radius effects and trapped particle resonances.
Trapped particles, in general have unfavorable magnetic drift, leading to the trapped particle instability, a localized low-frequency interchange. The most prominent type of long
wavelength toroidal microinstability is Trapped Ion driven Mode (TIM) in the presence of a significant ion temperature gradient. The initial work by Kadomtsev and Pogutse 1971 indicates that
the TIM mode has a real frequency below the diamagnetic drift frequency
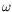 *and below the bounce frequency
*and below the bounce frequency
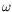
b. These instabilities are easier to excite in the core region of tokamak fusion plasmas where the plasma can be considered to be effectively collisionless. Thus these instabilities are
characterized by frequencies of the order of the trapped particle precession frequency and radial scales of the order of several banana widths. These properties make TIM modes have a global
nature
i.e.large radial correlation lengths that can vary on the equilibrium scale length rather than on the ion gyro-radius scale length usually associated with kinetic micro-instabilities.
It has been predicted that because of their large scales and in spite of their low frequencies, these instabilities could lead to a huge transport corresponding to a Bohm-like confinement
observed in many experiments. Such Trapped-ion driven modes are thus a simple prototype of kinetic instability since they are driven through the resonant interaction between a wave and
trapped ions via their precession motion and implies low toroidal numbers (
n<100), allowing fast numerical gyrokinetic simulations (see Depret el al 2000).
Although TIM have been studied during several decades, there exists a real interest today. Recently trapped particle modes seem to play a key role in nonambipolar transport in
ITER-relevant regimes, where strong enhancement of transport is thus predicted by bounce-harmonic resonance.
(ii) Another feature concerns the fact that turbulent transport can be greatly reduced in the presence of a magnetic shear. It is well known that the stabilization effect of the precession
drift reversal for trapped ion driven instabilities is efficient in nonlinear regime. Magnetic shear describes the dependence of field line direction on the coordinate across closed flux
surfaces. In a toroidal field with circular flux surfaces with minor and major radii
rand
R, the shear is defined as
 . The quantity
. The quantity
 is the winding number of magnetic field lines on any given flux surface,
i.e.the ratio of the displacement in toroidal angle to displacement in poloidal angle between two points on a field line. Thus, in a toroidal plasma, the magnetic field is not uniform.
Therefore, its magnitude varies both along and transverse to the field lines. The longitudinal variation traps particles (the projection of the guiding-center orbit onto a cross section at
fixed toroidal angle traces out a “banana” shape). While the transverse variation, referred to as magnetic shear, has a strong stabilization effect on collective instabilities. This effect
exists both in fluid and kinetic instabilities. For trapped particle drive instabilities (as TIM instabilities), it takes place through the reversal of the precession drift (see Kadomtsev and
Pogutse 1971).
is the winding number of magnetic field lines on any given flux surface,
i.e.the ratio of the displacement in toroidal angle to displacement in poloidal angle between two points on a field line. Thus, in a toroidal plasma, the magnetic field is not uniform.
Therefore, its magnitude varies both along and transverse to the field lines. The longitudinal variation traps particles (the projection of the guiding-center orbit onto a cross section at
fixed toroidal angle traces out a “banana” shape). While the transverse variation, referred to as magnetic shear, has a strong stabilization effect on collective instabilities. This effect
exists both in fluid and kinetic instabilities. For trapped particle drive instabilities (as TIM instabilities), it takes place through the reversal of the precession drift (see Kadomtsev and
Pogutse 1971).
(iii) Although 5D gyrokinetic simulations are now possible with realistic geometry, such simulations require huge CPU time and memory resources. The most mature kinetic approach is the
particle-in-cell (PIC) method. The method involves to integrate gyrokinetic Vlasov equation in time by advancing marker particles along a set of characteristics within the phase space. It
basically involves a lagrangian formulation in which the dynamics of an ensemble of gyro-averaged “particles” are tracked.
Several previous points were addressed in a gyrokinetic model of ITG instabilities for TIM model: forward cascade processes, condensation process of turbulence toward low toroidal modes,
turbulence stabilization for TIM modes due to reversed magnetic shear. Trapped-ion driven modes (TIMs) are studied by solving a Vlasov equation in action-angle variables using Hamiltonian
formalism (see Depret et al 2000). This Vlasov equation is then averaged over the fast scales: cyclotron and bounce motion for trapped ions. The distribution is then calculated as a function
of the poloidal flux
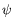 (normalized to
2
(normalized to
2
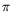 and which indeed plays the role of a radial coordinate) and the precession angle of
trapped ions
and which indeed plays the role of a radial coordinate) and the precession angle of
trapped ions
 , parametrized by the particle energy
, parametrized by the particle energy
Eand the trapping parameter
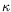 (depending of the adiabatic invariant
(depending of the adiabatic invariant
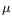 ).
).
The reduced gyrokinetic Vlasov equation is given by (see Garbet et al 1990, 1992, 1994 and 2001):

where the trapped ion distribution function is
 . The self-consistency constraint is
. The self-consistency constraint is

where we have introduced
 ,
,
npithe passing ion density and the gyro-averaged pseudo-density of trapped ions is given by:

In the previous expression we have
 where
where
 is the fraction of trapped ions. Consequently we have reduced the six-dimensional Vlasov equation into a set of 2D Vlasov equations (indeed
is the fraction of trapped ions. Consequently we have reduced the six-dimensional Vlasov equation into a set of 2D Vlasov equations (indeed
 equations) acting on a two-dimensional phase space
equations) acting on a two-dimensional phase space
 (precession angle
(precession angle
 , poloidal flux normalized to
2
, poloidal flux normalized to
2
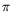 ), parametrized by the kinetic energy
), parametrized by the kinetic energy
Eand the trapping parameter
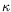 (
(
 with a chosen value of
with a chosen value of
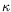
max= 0.975for numerical simulations).
 is the gyroaverage operator - multiplication by
is the gyroaverage operator - multiplication by
 - in Fourier space,
- in Fourier space,

cbeing the gyro-radius and
 the banana width. The present implementation of this operator is based on a Padé approximation of the Bessel function
the banana width. The present implementation of this operator is based on a Padé approximation of the Bessel function
J0. Eqs (
Here the density refers to the density of banana centers which do not correspond to the real density of particles. For instance Hahm and Tang 1996 use a Taylor expansion to give an
estimation of the potential value averaged along a field line in the form
 , which allows to take into account the difference between the real trapped ion particle density and the density of banana centers.
, which allows to take into account the difference between the real trapped ion particle density and the density of banana centers.
The trapped ion driven mode has been studied by solving a Vlasov equation averaged over the cyclotron and bounce motion of trapped particles in the presence of a magnetic shear. The
magnetic shear parameter appears to play a major role in the stabilization process of the instability and allows us to study the occurring of turbulence inside the system. The major mechanism
of turbulent transport is large-scale (electrostatic) convection of trapped particles. The dominant driving process is the temperature gradient over some critical value, and one of the
stabilizing elements is reversed magnetic shear. Turbulent plasma is obtained when the magnetic shear reaches a limit value which is positive. The introduction of the magnetic shear parameter
allows us to study the different regimes of turbulent transport from plasma state described by a small number of toroidal modes till the occurring of Kolmogorov-like cascade which implies the
excitation of a large band of toroidal modes (fully developed turbulence). This is achieved by using a semi-Lagrangian Vlasov code which allows a very accurate description of the trapped
particle distribution function in phase space.
Full wave modeling of lower hybrid current drive in tokamaks
This work is performed in collaboration with Yves Peysson (DRFC, CEA Cadarache). The goal of this work is to develop a full wave method to describe the dynamics of lower hybrid current
drive problem in tokamaks. The propagation and the absorption of the lower hybrid electromagnetic wave is a powerful method to generate current drive by wave-particle resonance. However since
the wavelength of the electromagnetic field at the LH frequency is very small, a conventional full wave analysis represents an extremely difficult numerical task, far beyond computer
capabilities. The problem is addressed in our work, by full wave calculations based on a mathematical finite element technique, allowing for the first time to treat a large volume of plasma.
This method is based on a mixed augmented variational (weak) formulation taking account of the divergence constraint and essential boundary conditions, which provides an original and
efficient scheme to describe in a global manner both propagation and absorption of electromagnetic waves in plasmas, without the WKB approximation, as done in the conventional ray tracing
techniques. This offers the possibility to investigate specific cases for which the usual description fails and may help therefore a general understanding of the LH physics. A first
application to a realistic small tokamak configuration is considered in
Application of Vlasov codes in nanophysics
Nicolas
Crouseilles
Paul-Antoine
Hervieux
Giovanni
Manfredi
Omar
Morandi
For a few works, our team has been involved in several research projects involving the application of Vlasov-like equations to the physics of nano-sized objects, such as thin metal films,
nanoparticles, quantum wells and quantum dots. It is a topic with tremendous potential for a broad spectrum of applications, ranging from materials science to biology and medicine. Our approach
– based on a phase-space description of the dynamics – is not widely used in the nanophysics community, which constitutes one of the originalities of our project.
Quantum hydrodynamics with spin
In previous years, a quantum hydrodynamical (QHD) model was used to investigate the self-consistent electron dynamics in a thin metal film
Breather mode in a confined quantum electron gas
This work was performed in collaboration with F. Haas and P. Shukla, from the Theoretical Physics Department of the Ruhr Universität, Bochum (Allemagne).
By using a version of the quantum hydrodynamic model, we have demonstrated the existence of a novel breather mode in the self-consistent dynamics of a confined electron gas. This mode
corresponds to oscillations of
sizeof the electron density, as measured by the variance
 . A variational method was used to determine the salient features of the electron breather mode. Numerical simulations of the time-dependent Wigner-Poisson equations were shown to be
in excellent agreement with our analytical results. For asymmetric confinement, a signature of the breather mode is observed in the dipole response, which can be detected by standard optical
means.
. A variational method was used to determine the salient features of the electron breather mode. Numerical simulations of the time-dependent Wigner-Poisson equations were shown to be
in excellent agreement with our analytical results. For asymmetric confinement, a signature of the breather mode is observed in the dipole response, which can be detected by standard optical
means.
These results have potential applications to the electron dynamics of nanosized semiconductor devices, such as quantum dots and quantum wells.
Ultrafast magnetization dynamics in diluted magnetic semiconductors
We have developed a dynamical model that successfully explains the observed time evolution of the magnetization in diluted magnetic semiconductor quantum wells after weak laser excitation.
Based on a many-particle expansion of the exact
p-
dexchange interaction, our approach goes beyond the usual mean-field approximation. It includes both the sub-picosecond demagnetization dynamics and the slower
relaxation processes which restore the initial ferromagnetic order on a nanosecond timescale. In agreement with experimental results, our numerical simulations show that, depending on the
value of the initial lattice temperature, a subsequent enhancement of the total magnetization may be observed on a timescale of few hundreds of picoseconds.
More recently, our model was augmented in order to include the role played by the quantum confinement and the band structure. It was shown that the sample thickness and the background hole
density strongly influence the phenomenon of demagnetization. Quantitative results were given for III-V ferromagnetic GaMnAs quantum wells of thickness 4 and 6 nm.
Inverse problem governed by Maxwell equations
Jean
Roche
This work is performed in collaboration with Jose Herskovits Norman (UFRJ, Rio de Janeiro, Bresil). Electromagnetic forces allow contactless heating, shaping and controlling of chemical
aggressive, hot melts. Applications of this industrial technique are electromagnetic shaping of aluminium ingots using soft-contact confinement of the liquid metal, electromagnetic shaping of
components of aeronautical engines made of superalloy materials (Ni,Ti,...), control of the structure solidification, etc ...
We study a two-dimensional magnetostatic inverse shaping problem: can one find a distribution of electric current in order that the horizontal cross-section of the molten metal have a
prescribed shape? This is a very important problem that one needs to solve in order to define a process of electromagnetic liquid metal forming. In addition, from a practical point of view, the
magnetic field has to be created by a simple configuration of inductors.
Under suitable assumptions, the equilibrated configurations are described by a set of equations expressing an equilibrium relation on the boundary between electromagnetic and surface tension
forces (and gravity in three-dimensional models). This equilibrium relation involves the curvature of the boundary and the solution of an elliptic exterior boundary value problem. The
equilibrated shape has been shown to be the stationary state of the total energy subject to the constraint that the surface area (the volume in three-dimensional problems) is prescribed.
The goal of this work is to give an algorithm to locate suitable inductors around the molten metal so that the equilibrated shape be as near as possible to a desired one. Two different
approaches are proposed, the first one seeks for a set of inductors such that the distance between the equilibrated shape and the given target one is minimized. The second approach looks for a
set of inductors such that a slack function related to the equilibrium relation on the boundary of the target shape is minimized.
In the two papers
![]() corresponding to the statistical average of the particle distribution in phase-space corresponding to many realisations of the physical system under investigation. The product
corresponding to the statistical average of the particle distribution in phase-space corresponding to many realisations of the physical system under investigation. The product
![]() is the average number of particles of the considered species, the position and velocity of which are located in a bin of volume
is the average number of particles of the considered species, the position and velocity of which are located in a bin of volume
![]() centered around
centered around
![]() . The distribution function contains a lot more information than what can be obtained from a fluid description, as it also includes information about the velocity distribution of the
particles.
. The distribution function contains a lot more information than what can be obtained from a fluid description, as it also includes information about the velocity distribution of the
particles.![]()

![]()
![]()
![]()
![]()
![]() are the characteristics of the Vlasov equation which are solution of the system of ordinary differential equations
are the characteristics of the Vlasov equation which are solution of the system of ordinary differential equations
![]() ,
,
![]() .
.![]() consisting in the following two steps:
consisting in the following two steps:![]() , i.e. an approximation of
, i.e. an approximation of
![]() ,
,
![]() .
.![]()
![]() .
.