Scientific Foundations
Introduction
In this section, the main features for the key monitoring issues, namely identification, detection, and diagnostics, are provided, and a particular instantiation relevant for vibration
monitoring is described.
It should be stressed that the foundations for identification, detection, and diagnostics, are fairly general, if not generic. Handling high order linear dynamical systems, in connection
with finite elements models, which call for using subspace-based methods, is specific to vibration-based SHM. Actually, one particular feature of model-based sensor information data processing
as exercised in I4S, is the combined use of black-box or semi-physical models together with physical ones. Black-box and semi-physical models are, for example, eigenstructure parameterizations
of linear MIMO systems, of interest for modal analysis and vibration-based SHM. Such models are intended to be identifiable. However, due to the large model orders that need to be considered,
the issue of model order selection is really a challenge. Traditional advanced techniques from statistics such as the various forms of Akaike criteria (AIC, BIC, MDL, ...) do not work at all.
This gives rise to new research activities specific to handling high order models.
Our approach to monitoring assumes that a model of the monitored system is available. This is a reasonable assumption, especially within the SHM areas. The main feature of our monitoring
method is its intrinsic ability to the early warning of small deviations of a system with respect to a reference (safe) behavior under usual operating conditions, namely without any artificial
excitation or other external action. Such a normal behavior is summarized in a reference parameter vector
 0, for example a collection of modes and mode-shapes.
0, for example a collection of modes and mode-shapes.
Identification
See module
The behavior of the monitored continuous system is assumed to be described by a parametric model
 , where the distribution of the observations (
, where the distribution of the observations (
Z0, ...,
ZN) is characterized by the parameter vector

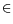
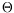 . An
estimating function, for example of the form :
. An
estimating function, for example of the form :

is such that
![Im3 ${\#119812 _\#952 {[\#119974 _N{(\#952 )}]}=0}$](math_image_3.png) for all
for all

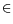
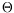 . In many situations,
. In many situations,
 is the gradient of a function to be minimized : squared prediction error, log-likelihood (up to a sign), .... For performing model identification on the basis of observations
(
is the gradient of a function to be minimized : squared prediction error, log-likelihood (up to a sign), .... For performing model identification on the basis of observations
(
Z
0, ...,
Z
N), an estimate of the unknown parameter is then

Assuming that
 *is the true parameter value, and that
*is the true parameter value, and that
![Im6 ${\#119812 _\#952 ^*{[\#119974 _N{(\#952 )}]}=0}$](math_image_6.png) if and only if
if and only if
 =
=
 *with
*with
 *fixed (identifiability condition), then
*fixed (identifiability condition), then
 converges towards
converges towards
 *. Thanks to the central limit theorem, the vector
*. Thanks to the central limit theorem, the vector
 is asymptotically Gaussian with zero mean, with covariance matrix
is asymptotically Gaussian with zero mean, with covariance matrix
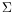 which can be either computed or estimated. If, additionally, the matrix
which can be either computed or estimated. If, additionally, the matrix
![Im9 ${\#119973 _N=-\#119812 _\#952 ^*{[{\#119974 }_N^'{(\#952 ^*)}]}}$](math_image_9.png) is invertible, then using a Taylor expansion and the constraint
is invertible, then using a Taylor expansion and the constraint
 , the asymptotic normality of the estimate is obtained :
, the asymptotic normality of the estimate is obtained :

In many applications, such an approach must be improved in the following directions :
Recursive estimation:the ability to compute
 simply from
simply from
 ;
;
Adaptive estimation:the ability to
trackthe true parameter
 *when it is time-varying.
*when it is time-varying.
Detection
See module
Our approach to on-board detection is based on the so-called asymptotic statistical local approach, which we have extended and adapted
For achieving the early detection of small deviations with respect to the normal behavior, our approach generates, on the basis of the reference parameter vector
 0and a new data record, indicators which automatically perform :
0and a new data record, indicators which automatically perform :
The early detection of a slight mismatch between the model and the data;
A preliminary diagnostics and localization of the deviation(s);
The tradeoff between the magnitude of the detected changes and the uncertainty resulting from the estimation error in the reference model and the measurement noise
level.
These indicators are computationally cheap, and thus can be embedded. This is of particular interest in some applications, such as flutter monitoring, as explained in module
As in most fault detection approaches, the key issue is to design a
residual, which is ideally close to zero under normal operation, and has low sensitivity to noises and other nuisance perturbations, but high sensitivity to small deviations, before they
develop into events to be avoided (damages, faults, ...). The originality of our approach is to :
Designthe residual basically as a
parameter estimating function,
Evaluatethe residual thanks to a kind of central limit theorem, stating that the residual is asymptotically Gaussian and reflects the presence of a deviation in the parameter vector
through a change in its own mean vector, which switches from zero in the reference situation to a non-zero value.
This is actually a strong result, which transforms any detection problem concerning a parameterized stochastic
processinto the problem of monitoring the mean of a Gaussian
vector.
The behavior of the monitored system is again assumed to be described by a parametric model
 , and the safe behavior of the process is assumed to correspond to the parameter value
, and the safe behavior of the process is assumed to correspond to the parameter value
 0. This parameter often results from a preliminary identification based on reference data, as in module
0. This parameter often results from a preliminary identification based on reference data, as in module
Given a new
N-size sample of sensors data, the following question is addressed :
Does the new sample still correspond to the nominal model
 ?One manner to address this generally difficult question is the following. The asymptotic local approach consists in deciding between the nominal hypothesis and a
closealternative hypothesis, namely :
?One manner to address this generally difficult question is the following. The asymptotic local approach consists in deciding between the nominal hypothesis and a
closealternative hypothesis, namely :

where
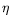 is an unknown but fixed change vector. A residual is generated under the form :
is an unknown but fixed change vector. A residual is generated under the form :

If the matrix
![Im16 ${\#119973 _N=-~\#119812 _\#952 _0{[{\#119974 }_N^'{(\#952 _0)}]}}$](math_image_16.png) converges towards a limit
converges towards a limit
 , then the central limit theorem shows
, then the central limit theorem shows

where the asymptotic covariance matrix
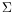 can be estimated, and manifests the deviation in the parameter vector by a change in its own mean value. Then, deciding between
can be estimated, and manifests the deviation in the parameter vector by a change in its own mean value. Then, deciding between
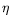 = 0and
= 0and
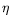
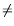 0amounts to compute the following
0amounts to compute the following
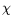 2-test, provided that
2-test, provided that
 is full rank and
is full rank and
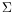 is invertible :
is invertible :

where

With this approach, it is possible to decide, with a quantifiable error level, if a residual value is significantly different from zero, for assessing whether a fault/damage has occurred. It
should be stressed that the residual and the sensitivity and covariance matrices
 and
and
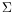 can be evaluated (or estimated) for the nominal model. In particular, it is
notnecessary to re-identify the model, and the sensitivity and covariance matrices can be pre-computed off-line.
can be evaluated (or estimated) for the nominal model. In particular, it is
notnecessary to re-identify the model, and the sensitivity and covariance matrices can be pre-computed off-line.
Diagnostics
See modules
A further monitoring step, often called
fault isolation, consists in determining which (subsets of) components of the parameter vector
 have been affected by the change. Solutions for that are now described. How this relates to diagnostics is addressed afterwards.
have been affected by the change. Solutions for that are now described. How this relates to diagnostics is addressed afterwards.
Isolation.
The question:
which (subsets of) components of
 have changed ?, can be addressed using either nuisance parameters elimination methods or a multiple hypotheses testing approach
have changed ?, can be addressed using either nuisance parameters elimination methods or a multiple hypotheses testing approach
The fault vector
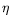 is partitioned into an informative part and a nuisance part, and the sensitivity matrix
is partitioned into an informative part and a nuisance part, and the sensitivity matrix
 , the Fisher information matrix
, the Fisher information matrix
 and the normalized residual
and the normalized residual
 are partitioned accordingly
are partitioned accordingly

A rather intuitive statistical solution to the isolation problem, which can be called
sensitivityapproach, consists in projecting the deviations in
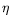 onto the subspace generated by the components
onto the subspace generated by the components
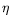
ato be isolated, and deciding between
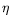
a=
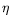
b= 0and
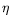
a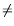 0,
0,
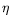
b= 0. This results in the following test statistics :

where
 is the partial residual (score). If
is the partial residual (score). If
ta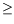
tb, the component responsible for the fault is considered to be
arather than
b.
Another statistical solution to the problem of isolating
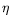
aconsists in viewing parameter
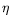
bas a nuisance, and using an existing method for inferring part of the parameters while ignoring and being robust to the complementary part. This method is called
min-max approach. It consists in replacing the nuisance parameter component
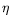
bby its least favorable value, for deciding between
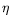
a= 0and
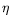
a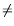 0, with
0, with
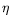
bunknown. This results in the following test statistics :

where
 is the effective residual (score) resulting from the regression of the informative partial score
is the effective residual (score) resulting from the regression of the informative partial score
 over the nuisance partial score
over the nuisance partial score
 , and where the Schur complement
, and where the Schur complement
 is the associated Fisher information matrix. If
is the associated Fisher information matrix. If
ta*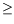
tb*, the component responsible for the fault is considered to be
arather than
b.
The properties and relationships of these two types of tests are investigated in
Diagnostics.
In most SHM applications, a complex physical system, characterized by a generally non identifiable parameter vector
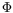 has to be monitored using a simple (black-box) model characterized by an identifiable parameter vector
has to be monitored using a simple (black-box) model characterized by an identifiable parameter vector
 . A typical example is the vibration monitoring problem in module
. A typical example is the vibration monitoring problem in module
 and diagnosis in terms of the parameter vector
and diagnosis in terms of the parameter vector
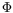 of the underlying physical model.
of the underlying physical model.
The isolation methods sketched above are possible solutions to the former. Our approach to the latter diagnosis problem is basically a detection approach again, and not a (generally
ill-posed) inverse problem estimation approach
 , where
, where
 is the Jacobian matrix at
is the Jacobian matrix at
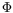 0of the application
0of the application
 , and to use the sensitivity test (
, and to use the sensitivity test (
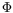 . Typically this results in the following type of directional test :
. Typically this results in the following type of directional test :

It should be clear that the selection of a particular parameterization
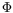 for the physical model may have a non negligible influence on such type of tests, according to the numerical conditioning of the Jacobian matrices
for the physical model may have a non negligible influence on such type of tests, according to the numerical conditioning of the Jacobian matrices
 .
.
As a summary, the machinery in modules
The key issue to be addressed within each parametric model class is the residual generation, or equivalently the choice of the
parameter estimating function.
Subspace-based identification and detection
See module
For reasons closely related to the vibrations monitoring applications described in module
 of the state transition matrix
of the state transition matrix
Fof a linear dynamical state-space system :

namely the
 defined by :
defined by :

The (canonical) parameter vector in that case is :

where
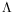 is the vector whose elements are the eigenvalues
is the vector whose elements are the eigenvalues
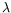 ,
,
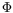 is the matrix whose columns are the
is the matrix whose columns are the
 's, and
vecis the column stacking operator.
's, and
vecis the column stacking operator.
Subspace-based methods is the generic name for linear systems identification algorithms based on either time domain measurements or output covariance matrices, in which different subspaces
of Gaussian random vectors play a key role
Covariance-driven subspace identification.
Let
 and:
and:

be the output covariance and Hankel matrices, respectively; and:
 . Direct computations of the
. Direct computations of the
Ri's from the equations (

where:

are the observability and controllability matrices, respectively. The observation matrix
His then found in the first block-row of the observability matrix
 . The state-transition matrix
. The state-transition matrix
Fis obtained from the shift invariance property of
 . The eigenstructure
. The eigenstructure
 then results from (
then results from (
Since the actual model order is generally not known, this procedure is run with increasing model orders.
Model parameter characterization.
Choosing the eigenvectors of matrix
Fas a basis for the state space of model (

where
 , and
, and
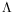 and
and
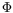 are as in (
are as in (
 0fits a given output covariance sequence
(
0fits a given output covariance sequence
(
R
j)
jis characterized by

This property can be checked as follows. From the nominal
 0, compute
0, compute
 using (
using (
 for extracting a matrix
for extracting a matrix
Usuch that:

Matrix
Uis not unique (two such matrices relate through a post-multiplication with an orthonormal matrix), but can be regarded as a function of
 0. Then the characterization writes:
0. Then the characterization writes:

Residual associated with subspace identification.
Assume now that
a reference
 0and a new sample
0and a new sample
 are available.For checking whether the data agree with
are available.For checking whether the data agree with
 0, the idea is to compute the empirical Hankel matrix
0, the idea is to compute the empirical Hankel matrix
 :
:

and to define the residual vector:

Let
 be the actual parameter value for the system which generated the new data sample, and
be the actual parameter value for the system which generated the new data sample, and
 be the expectation when the actual system parameter is
be the expectation when the actual system parameter is
 . From (
. From (
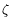
N(
 0)has zero mean when no change occurs in
0)has zero mean when no change occurs in
 , and nonzero mean if a change occurs. Thus
, and nonzero mean if a change occurs. Thus
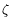
N(
 0)plays the role of a residual.
0)plays the role of a residual.
It is our experience that this residual has highly interesting properties, both for damage detection
Other uses of the key factorizations.
Factorization (
 in (
in (
Proving consistency and robustness results
Designing an extension of covariance-driven subspace identification algorithm adapted to the presence and fusion of non-simultaneously recorded multiple sensors setups
Proving the consistency and robustness of this extension
Designing various forms of
input-outputcovariance-driven subspace identification algorithms adapted to the presence of both known inputs and unknown excitations
Application Domains
Introduction
In this section, the problems we are faced with vibration-based monitoring and within our two major application domains are briefly described.
Vibrations-based monitoring
See modules
Detecting and localizing damages for monitoring the integrity of structural and mechanical systems is a topic of growing interest, due to the aging of many engineering constructions and
machines and to increased safety norms. Many current approaches still rely on visual inspections or
localnon destructive evaluations performed manually. This includes acoustic, ultrasonic, radiographic or eddy-current methods; magnet or thermal field techniques,
.... These experimental approaches assume an
a prioriknowledge and the accessibility of a neighborhood of the damage location. Automatic
globalvibration-based monitoring techniques have been recognized to be useful alternatives to those local evaluations
A common feature of the structures to be monitored (e.g. civil engineering structures subject to hurricanes or earthquakes, but also swell, wind and rain; aircrafts subject to strength and
turbulences,
...) is the following. These systems are subject to both fast and unmeasured variations in their environment and small slow variations in their vibrating
characteristics. The available data (measurements from e.g. strain gauges or accelerometers) do not separate the effects of the external forces from the effect of the structure. The external
forces vary more rapidly than the structure itself (fortunately !), damages or fatigues on the structure are of interest, while any change in the excitation is meaningless. Expert systems
based on a human-like exploitation of recorded spectra can hardly work in such a case : the changes of interest (1% in eigenfrequencies) are visible neither on the signals nor on their
spectra. A global health monitoring method must rather rely on a model that will help in discriminating between the two mixed causes of the changes that are contained in the measurements.
Classical modal analysis and vibration monitoring methods basically process data registered either on test beds or under specific excitation or rotation speed conditions. However there is a
need for vibration monitoring algorithms devoted to the processing of data recorded in-operation, namely during the actual functioning of the considered structure or machine, without artificial
excitation, speeding down or stopping.
Health monitoring techniques based on processing vibration measurements basically handle two types of characteristics: the
structural parameters(mass, stiffness, flexibility, damping) and the
modal parameters(modal frequencies, and associated damping values and mode-shapes); see
Controlling the computational complexity of the processing of the collected data is another standard monitoring requirement, which includes a limited use of an analytical model of the
structure. Moreover, the reduction from the analytical model to the experimental model (truncated modal space) is known to play a key role in the success of model-based damage detection and
localization.
The approach which we have been developing, based on the foundations in modules
Civil engineering
See modules
Civil engineering is a currently renewing scientific research area, which can no longer be restricted to the single mechanical domain, with numerical codes as its central focus. Recent and
significant advances in physics and physical chemistry have improved the understanding of the detailed mechanisms of the constitution and the behavior of various materials (see e.g. the
multi-disciplinary general agreement
cnrs-Lafarge). Moreover, because of major economical and societal issues, such as durability and safety of infrastructures, buildings and networks,
civil engineering is evolving towards a multi-disciplinary field, involving in particular information sciences and technologies and environmental sciences.
These last ten years, monitoring the integrity of the civil infrastructure has been an active research topic, including in connected areas such as automatic control, for mastering either the
aging of the bridges, as in America (US, Canada) and Great Britain, or the resistance to seismic events and the protection of the cultural heritage, as in Italy and Greece. The research effort
in France seems to be more recent, maybe because a tendency of long term design without fatigue oriented inspections, as opposite to less severe design with planned mid-term inspections. One of
the current thematic priorities of the Réseau de Génie Civil et Urbain (RGCU) is devoted to constructions monitoring and diagnostics. The picture in Asia (Japan, and also China) is somewhat
different, in that the demand for automatic data processing for global SHM systems is much higher, because recent or currently built bridges are equipped with hundreds if not thousands of
sensors, in particular the Hong Kong-Shenzen Western Corridor and Stonecutter Bridge projects.
Among the challenges for vibration-based bridges health monitoring, two major issues are the different kinds of (non measured) excitation sources and the environmental effects
Aeronautics
See modules
The aging of aerospace structures is a major current concern of civilian and military aircraft operators. Another key driving factor for SHM is to increase the operation and support
efficiency of an air vehicle fleet. A SHM system is viewed as a component of a global integrated vehicle health management (IVHM) system. An overview of the users needs can be found in
Improved safety and performance and reduced aircraft development and operating costs are other major concerns. One of the critical design objectives is to clear the aircraft from unstable
aero-elastic vibrations (flutter) in all flight conditions. This requires a careful exploration of the dynamical behavior of the structure subject to vibration and aero-servo-elastic forces.
This is achieved via a combination of ground vibration tests and in-flight tests. For both types of tests, various sensors data are recorded, and modal analyses are performed. Important
challenges of the in-flight modal analyses are the limited choices for measured excitation inputs, and the presence of unmeasured natural excitation inputs (turbulence). A better exploitation
of flight test data can be achieved by using output-only system identification methods, which exploits data recorded under natural excitation conditions (e.g., turbulent), without resorting to
artificial control surface excitation and other types of excitation inputs
A crucial issue is to ensure that the newly designed airplane is stable throughout its operating range. A critical instability phenomenon, known under the name of
“aero-elastic flutter, involves the unfavorable interaction of aerodynamic, elastic, and inertia forces on structures to produce an unstable oscillation that often results in structural
failure”
Until the late nineties, most approaches to flutter clearance have led to
data-basedmethods, processing different types of data. A
combined data-based and model-basedmethod has been introduced recently under the name of flutterometer. Based on an aero-elastic state-space model and on frequency-domain transfer
functions extracted from sensor data under controlled excitation, the flutterometer computes on-line a robust flutter margin using the
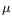 -method for analyzing the worst case effects of model uncertainty. In recent comparative evaluations using simulated and real data
-method for analyzing the worst case effects of model uncertainty. In recent comparative evaluations using simulated and real data
Algorithms achieving the
on-line in-flightexploitation of flight test data are expected to allow a more direct exploration of the flight domain, with improved confidence and reduced costs. Among other
challenges, one important issue to be addressed on-line is the flight flutter monitoring problem, stated as the problem of monitoring some specific damping coefficients. On the other hand, it
is known, e.g. from Cramer-Rao bounds, that damping factors are difficult to estimate accurately. For improving the estimation of damping factors, and moreover for achieving this in real-time
during flight tests, one possible although unexpected route is to rely on detection algorithms able to decide whether some damping factor decreases below some critical value or not. The
rationale is that detection algorithms usually have a much shorter response time than identification algorithms. This is addressed in module
Software
COSMAD: Modal analysis and health monitoring Scilab toolbox
Laurent
Mevel
corresponding person
Neil
Babou
Maurice
Goursat
With the help of Yann Veillard, Auguste Sam and Simon Berger, former engineers, Laurent Mevel and Maurice Goursat have developed a Scilab toolbox devoted to modal analysis and vibration
monitoring of structures or machines subjected to known or ambient (unknown) excitation
This software (COSMAD 3.64) has been registered at the APP under the number
IDDN.FR.001.210011.002.S.A.2003.000.20700
and can be down-loaded from
[http://
www.
irisa.
fr/
i4s/
cosmad/
]. A list of test-cases (simulators, laboratory test-beds, real structures) for which COSMAD has been used is available from
[http://
www.
irisa.
fr/
i4s/
cases.
pdf].
COSMAD performs the following tasks :
Output-only (O/O) subspace-based identification, working batch-wise, see modules
Input-output (I/O) subspace-based identification, working batch-wise, see modules
Automatic subspace-based modal analysis, a pre-tuned version of the O/O and I/O identification methods above. This is described in
Automated on-line identification package, see modules
Automatic recursive subspace-based modal analysis, a sample point-wise version of the O/O and I/O identification algorithms above. For this method, see
Subspace-based identification through moving sensors data fusion, see modules
Damage detection, working batch-wise, see modules
Based on vibrations measurements processing, the problem is to perform early detection of small deviations of the structure w.r.t. a reference behavior considered as normal. Such an
early detection of small deviations is mandatory for fatigue prevention. The algorithm confronts a new data record, summarized by covariance matrices, to a reference modal signature. The
method is described in
Damage monitoring, a sample point-wise version of the damage detection algorithm above. This is described in
On-line flutter onset detection, see modules
Modal diagnosis, working batch-wise, see modules
Damage localization, see modules
The problem is to find the part of the structure, and the associated structural parameters (e.g. masses, stiffness coefficients) that have been affected by the damage. We state and solve
this problem as a detection problem, and not an (ill-posed) inverse estimation problem. This is explained in
Optimal sensor positioning for monitoring. At the design stage of the monitoring system, a criterion is computed, which quantifies the relevance of a given sensor number and
positioning for the purpose of structural health monitoring. For this criterion, see the articles
The modules have been tested by different partners, especially the French industrial partners, EADS, Dassault and Sopemea, within the FliTE2 project (see module
This Scilab toolbox continues to play the role of a programming and development environment for all our newly designed algorithms. Moreover, offering a
maintainedScilab platform turns out to be a crucial factor in convincing industrial partners to undergo joint investigations with us or to involve us within partnerships in FP7
integrated projects proposals, see module
As from December 2007, Neil Babou, associate engineer, has worked on finalizing the next major version of COSMAD. Identification techniques used during FliTE2 have also been implemented by
F. Queyroi. Porting COSMAD to Scilab 5 has been done. A specific version for use within SNECMA is currently under way.
New Results
Eigenstructure identification
Michael
Döhler
Maurice
Goursat
Laurent
Mevel
See modules
Improving subspace identification : slight modifications of the algorithm
There are numerous ways to implement the covariance subspace identification method. The variants relate to the choice of parameters, which have to be tuned by the user. Such tuning is only
reliably done by the mechanical engineer, when the parameter has a physical meaning. From the data to the results there are 4 main steps in the covariance subspace identification method. In
this paper
Monitoring of aerospace rockets
We revisit the problem of the modal analysis of space launchers. We consider the Ariane 5 launcher with its usual equipment during a commercial flight under the natural unknown excitation.
The case of space launchers is a typical example of a complex structure with sub-structures strongly and quickly varying in time. This issue becomes especially important in e.g. estimation of
damping of aerospace vehicles. The eigenfrequencies are also sliding during the flight but the modeshapes are more stable. Recently, a new implementation of the subspace identification method
has been proposed, leading to cleaner and more stable stabilization diagrams. We monitor the behavior of estimated modal parameters by applying this crystal clear implementation of the data
driven and the covariance driven Stochastic Subspace Identification algorithms. We show the importance of crystal clear to monitor successfully frequencies and damping estimates over time in
such a non stationary case. This work will be presented in
Large structures identification - Data fusion
Michael
Döhler
Laurent
Mevel
See modules
In Operational Modal Analysis (OMA) of large structures we often need to process sensor data from multiple non simultaneously recorded measurement setups. These setups share some sensors in
common, the so-called reference sensors that are fixed for all the measurements, while the other sensors are moved from one setup to the next. To obtain the modal parameters of the investigated
structure, it is necessary to process the data of all the measurement setups and normalize it as the unmeasured background excitation of each setup might be different. For this we compare three
different approaches which differ in the order of the data merging, normalization and system identification step: The classical PoSER (identification-normalization-merging), the PoGER
(merging-identification-normalization) and the PreGER (normalization-merging-identification). Special care was taken with the PreGER method and its efficiency has been tested with respect to
the two other methods. The system identification is done with the SSI-cov/ref method. We apply these methods to the extraction of the modal parameters (natural frequencies, damping ratios and
mode shapes) of the Luiz I arch bridge in Porto, Portugal, compare them and evaluate the different methods
A variant of this approach has been derived to handle different subspace approaches such as the UPC data driven approach. It has been tested on a building in Vancouver and presented in
Change/damage detection and isolation in the frequency domain
Gilles
Canales
Laurent
Mevel
See modules
The first year of the PhD thesis of G. Canales has been focused on understanding and developing some detection tests in the frequency domain. Indeed, advances in engineering have led to the
increase in monitoring capacities (number of sensors). This calls for developing new and more efficient approaches to the monitoring problem. One such approach was to try to work out a
frequency domain damage detection test.
A new residual based on the polyreference Least Square Complex Frequency domain (LSCF) identification method has been proposed and described in the 2007 report. It has been presented at
In the second year of Gilles Canales thesis, different frequency domain damage detection residuals have been derived for the transmissibility frequency domain method. It has been presented
at
Consistency and asymptotical normality of that residual have been proved. We monitor some small changes in the transmissibility equation, where the transmissibility is the ratio between
output and input in the frequency domain. Assuming a single force is applied to the system, this leads to an output only frequency domain method, a relaxing hypothesis with respect to last year
Other frequency domain methods under investigation include OMAX, Maximum likelihood and frequency domain decomposition methods. Residuals for such techniques have been evaluated. G. Canales
is currently writing his thesis.
Composite structures
Michael
Döhler
Maurice
Goursat
Laurent
Mevel
See modules
A comparison of three different damage detection methods is made on three identical glass reinforced composite panels, similar to the load carrying laminate in a wind turbine blade. Sensor
data were recorded in the healthy state and after the introduction of damage by means of a four point bending quasi static test. Acceleration sensors, PZT transducers and the piezoelectric
excited Lamb waves were used for the measurements of the panels. All three methods are based on the comparison of the healthy and damaged structure. The first method is statistical covariance
driven damage detection using a subspace based algorithm, where one damage indicator for all three panels was computed. The second method is based on PZT transducers and the A0 mode of Lamb
waves propagating in the panel, making use of the reflection of the signal at damage in the panel. The third method is based on the estimation of modal parameters of the intact and damaged
panel using pLSCF and following their deviations. The results from these three damage detection methods are compared and discussed. This work will be presented in
Flutter monitoring and onset detection
Michèle
Basseville
Laurent
Mevel
Rafik
Zouari
See modules
Stating the flutter monitoring problem (see modules
Adaptive online CUSUM tests.
A new empirical approach to kernel computation has been evaluated and presented at the IFAC World Congress
t, with a recursive computation of its kernel. The kernel is representative of the modal state at some previous instant. If some brutal change arises, a discrepancy appears between the
Hankel matrix and its kernel because of the delay between both computations. The test is not performing flutter detection but monitors the brutal variations of the monitored parameter, which
will be the flutter phenomena if we assume that flutter corresponds to a brusque variation in the dynamics of the parameter. An application to a large scale simulated aircraft has been
performed during the FliTE2 project and presented at EWSHM in Poland. This was done in collaboration with AGH
Work is currently ongoing to publish this work.
Subspace based damping monitoring
Tracking the evolutions of modal parameters is not an easy task. In fact, even for stationary systems, identification is a complex task, notwithstanding the computation of confidence
intervals. For non stationary systems, such as an aircraft in operation, reaction time and system variability render most identification methods difficult to implement. The CUSUM technique is
reused to handle monitoring of slight in-operation modal variations over time. Application to simulation data shows the relevance of the new approach to track damping coefficients of critical
modes. The methods involves the computation of a parametrized reference kernel for the CUSUM test, tuned with some signature representative of some predefined threshold corresponding to a
confidence interval for the monitored damping. Minmax rejection allows the rejection of the effect of the frequency evaluation due to the mismatch between the modal model defined by the
parameterized kernel and the current model associated with the data, resulting from the interaction with the aeroelasticity model. This method of tracking modal parameter variations by a
change detection technique defined by some predefined adaptive threshold has been validated on both academic examples and some realistic simulation of an aircraft under acceleration phase
provided by Dassault Aviation. This work has been presented at
Handling the temperature effect
Michael
Döhler
Maurice
Goursat
Laurent
Mevel
See modules
The PhD thesis of Houssein Nasser completed in 2006 has addressed the problem of rejecting the temperature effect when performing damage detection tests on civil structures. Because of the
temperature effects, the test may not react to some damages, and conversely may be too sensitive to some ambient temperature changes.
Some approach is based on the collection of varying reference temperature datasets, and on a reference kernel averaging all the temperature scenarios
Temperature rejection : case study on a bridge
After the work on a beam under temperature and damages changes in I4S and LCPC
Temperature rejection : case study on a bridge mock up
Small localized damages are hardly detected by global monitoring methods. The effectiveness of vibration based detection depends on the accuracy of the modal parameter estimates and is
limited by the low sensitivity of the modal parameters to a local stiffness reduction. A local reduction of stiffness related to frequency changes less than
1%was successfully detected on a 10 meter span composite UHPFRC - FRP reinforced timber beam bridge loaded in laboratory conditions up to the serviceability limit
state (SLS). Such a small decrease in the stiffness was not detected by the monitoring of the static load-deflection measurements but was confirmed by non-linear local strain measurements.
Statistical subspace-based damage detection successfully detected the change of the modal parameters of the investigated structure. Further analysis with a finite element model was conducted
for assessing the consistency of the expected location and extent of the damaged elements. Work will be presented in
Contracts and Grants with Industry
Eurêka project FliTE2
Michèle
Basseville
Albert
Benveniste
Maurice
Goursat
Laurent
Mevel
Rafik
Zouari
See modules
Contract INRIA — September 2005/November 2008.
We have been strongly contributing to the establishment, within the Eurêka framework, of a follow-up of the major cooperation FliTE for which a success story is available at
[http://
www.
eurekanetwork.
org/
].
The Eurêka project no 3341 FliTE2 ( Flight Test Easy Extension) is devoted to improving the exploitation of flight test data, under natural excitation conditions (e.g. turbulence),
enabling more direct exploration of the flight domain, with improved confidence and at reduced cost.
This project is finished, but work is still going on for publishing results of Rafik zouari thesis. A new FP7 project proposal is under consideration.
FP7-NMP CP-IP 213968-2 IRIS
Michael
Döhler
Laurent
Mevel
Xuan Binh
Lam
See modules
Contract INRIA 3947
I4S is involved in the core consortium of FP7-NMP Large Scale Integrated Project IRIS (
Integrated European Industrial Risk Reduction System), which helds its kick off meeting in October 2008. This project has been elaborated within the framework of the SAMCO association
(see module
A new PhD student, Xuan Binh Lam, has started from November 1st, 2008, willing to work on safety related work for risk control, especially for monitoring of transient events.
The FP7 IRIS project about Risk assessment involves 40 partners and is headed by Helmut Wenzel, VCE (Austria). INRIA is involved in Group 3 about Structural Health Monitoring. I4S works with
Sheffield University and BAM (Germany) for development of tools for structural damage detection for bridges and wind farms. Laurent Mevel is also member of the core IRIS Vision group, and is
responsible of the scientific coherency of the project.
SIMS
Laurent
Mevel
See modules
SIMS, Canada : I4S has signed a collaborative agreement with SVIBS. This leads to SVIBS bringing INRIA into a 12 year long SHM project in Canada with ambitious objectives of producing some
full internet based structural health monitoring project with potential applications to buildings, hospitals and of course, the collection of bridges monitored by the Ministry of Transportation
of British Columbia. This project is also related to TPV, a startup in civil engineering, whose objectives is to valuate our methods in North America.
This project is monitored by University of British Columbia, under contract with Ministry of Transportation, BC. This work is performed with help of DDS, Belgium and SVIBS, DK. This will
implement INRIA algorithms in a SHM system, and will provide a large scale outdoor demonstration for I4S.
PhD CIFRE with Dassault Aviation
Laurent
Mevel
See modules
Following the FliTE2 project, discussions are under way about a joint PhD thesis between INRIA and Dassault Aviation. The thesis will pursue the work achieved in FliTE2 and starts in Fall
2010 funded by Dassault Aviation.
Pôle de Compétitivité ASTECH MODIPRO
Maurice
Goursat
Laurent
Mevel
See modules
Contract INRIA 4162
I4S is implied in a national project for aircraft SHM starting Fall 2009. This project will improve on monitoring procedures developed in previous projects to provide some algorithms for use
in Dassault Aviation aircraft monitoring procedures.
SNECMA
Neil
Babou
Maurice
Goursat
Laurent
Mevel
See modules
Contract INRIA to be signed December 2009.
In 2007, I4S has investigated for SNECMA an identification case study on some undisclosed engine structure. Successfull results yield to the delivery of the COSMAD toolbox for internal
evaluation at SNECMA. The end goal is the use of COSMAD in the industrial process of SNECMA. Internal evaluation of COSMAD has been performed inhouse by SNECMA in 2008. A contract has been
signed and some software package will be developed to suit SNECMA needs in 2010. Work on the SNECMA prototype has been performed in 2009.
SVIBS
Laurent
Mevel
See modules
Annual agreement INRIA-SVIBS 2381 + contract 4329
SVIBS (Structural Vibration Solutions A/S) is a company located in Aalborg, Denmark, having strong connections with the Department of Civil Engineering of University of British Columbia, CA
(Prof. Carlos Ventura).
SVIBS and I4S are investigating how to link the modal analysis software ARTeMIS of SVIBS and COSMAD. Through an annual agreement, I4S gets a license of ARTeMIS in exchange to offer support
for integrating our damage detection software into SVIBS software and offerings. A contract has been signed, where I4S provides algorithms and expertise for integration within a damage
detection structural health monitoring system and SVIBS does the implementation. This technology transfer has been funded by the ministry of transportation of British Columbia, Canada. The work
is supervised by UBC, CA. The end product will be a web based structural health monitoring system for in operation bridges.
I4S is doing technology transfer towards SVIBS to implement I4S technologies into ARTEMIS Extractor Pro. This is done under a royalty agreement between INRIA and SVIBSḞirst achievements
include the implementation of the so called Crystal Clear SSI, a subspace variant, with much lower signal to noise ratio, and whose interest in the mechanical engineering community is very
high. Other I4S algorithms are currently under review to be integrated within ARTEMIS. SVIBS and I4S are also related in the related IAPP proposal and the SIMS project.
Other Grants and Activities
SAMCO association
See modules
The FP5 Growth thematic network SAMCO has been active from October 2001 until March 2006 within the framework of the Growth program. It has become a focal point of reference in the
field of assessment, monitoring and control of civil and industrial structures, in particular the transportation infrastructure (bridges, etc.). The European Association for SAMCO was founded
on April 2006. We are involved especially in the thematic group «Monitoring and Assessment». This turns out to be a useful complement to the diffusion of our knowledge and expertise in
vibration monitoring.
Within this framework, we have offered Scilab as an open platform for the integration of the modules for algorithms and methods covering the objectives of automatic modal analysis, automatic
modal and statistical damage detection methods. We have also offered the COSMAD toolbox, see module
We are involved in the IRIS project proposal, elaborated in this framework, see module
FWO Research Network ICCoS
Albert
Benveniste
Laurent
Mevel
We participate to the Scientific Research Network Identification and Control of Complex Systems (ICCoS) launched by the Research Foundation of Flanders (FWO). This network is dedicated to
national and international cooperation at postdoctoral level for the development of identification and control design methodologies.
Partnership with KU Leuven
Maurice
Goursat
Laurent
Mevel
Agreement INRIA-KU.Leuven
I4S and Katholieke Universiteit Leuven (Guido de Roeck, Civil Engineering Department) are collaborating on the topic of confidence intervals for subspace-based estimates
Marie Curie FP7-PEOPLE-2009-IAPP ISMS
Michael
Döhler
Laurent
Mevel
See modules
A proposal has been submitted with SVIBS, University of British Columbia and I4S to develop a framework for handling structural health monitoring methods. This proposal implies some long
stay of the concerned people, Laurent Mevel and Michael Döhler for I4S abroad. Palle Andersen from SVIBS is assumed to stay 4 months at INRIA, for tighten integration of COSMAD and ARTEMIS
software.
International collaborations
Michael
Döhler
Maurice
Goursat
Laurent
Mevel
This year, I4S has been collaborating with the following universities and institutes :
The University of British Columbia (CA), Civil Engineering Department,
Vrije Universiteit Brussel (B), Acoustics & Vibration Research Group,
Minho University (PT), Civil Engineering Department
Katholieke Universiteit Leuven (B), Civil Engineering Department
LCPC, Metrology and Instrumentation Division
Faculty of Engineering of University of Porto
![]() 0, for example a collection of modes and mode-shapes.
0, for example a collection of modes and mode-shapes.![]() , where the distribution of the observations (
, where the distribution of the observations (
![]()
![]()
![]() . An
estimating function, for example of the form :
. An
estimating function, for example of the form :![]()
![]() for all
for all
![]()
![]()
![]() . In many situations,
. In many situations,
![]() is the gradient of a function to be minimized : squared prediction error, log-likelihood (up to a sign), .... For performing model identification on the basis of observations
(
is the gradient of a function to be minimized : squared prediction error, log-likelihood (up to a sign), .... For performing model identification on the basis of observations
(
![]()
![]() *is the true parameter value, and that
*is the true parameter value, and that
![]() if and only if
if and only if
![]() =
=
![]() *with
*with
![]() *fixed (identifiability condition), then
*fixed (identifiability condition), then
![]() converges towards
converges towards
![]() *. Thanks to the central limit theorem, the vector
*. Thanks to the central limit theorem, the vector
![]() is asymptotically Gaussian with zero mean, with covariance matrix
is asymptotically Gaussian with zero mean, with covariance matrix
![]() which can be either computed or estimated. If, additionally, the matrix
which can be either computed or estimated. If, additionally, the matrix
![]() is invertible, then using a Taylor expansion and the constraint
is invertible, then using a Taylor expansion and the constraint
![]() , the asymptotic normality of the estimate is obtained :
, the asymptotic normality of the estimate is obtained :![]()
![]() simply from
simply from
![]() ;
;![]() *when it is time-varying.
*when it is time-varying.![]() 0and a new data record, indicators which automatically perform :
0and a new data record, indicators which automatically perform :![]() , and the safe behavior of the process is assumed to correspond to the parameter value
, and the safe behavior of the process is assumed to correspond to the parameter value
![]() 0. This parameter often results from a preliminary identification based on reference data, as in module
.
0. This parameter often results from a preliminary identification based on reference data, as in module
.![]() ?One manner to address this generally difficult question is the following. The asymptotic local approach consists in deciding between the nominal hypothesis and a
closealternative hypothesis, namely :
?One manner to address this generally difficult question is the following. The asymptotic local approach consists in deciding between the nominal hypothesis and a
closealternative hypothesis, namely :![]()
![]() is an unknown but fixed change vector. A residual is generated under the form :
is an unknown but fixed change vector. A residual is generated under the form :![]()
![]() converges towards a limit
converges towards a limit
![]() , then the central limit theorem shows
that the residual is asymptotically Gaussian :
, then the central limit theorem shows
that the residual is asymptotically Gaussian :
![]() can be estimated, and manifests the deviation in the parameter vector by a change in its own mean value. Then, deciding between
can be estimated, and manifests the deviation in the parameter vector by a change in its own mean value. Then, deciding between
![]() = 0and
= 0and
![]()
![]() 0amounts to compute the following
0amounts to compute the following
![]() 2-test, provided that
2-test, provided that
![]() is full rank and
is full rank and
![]() is invertible :
is invertible :![]()
![]()
![]() and
and
![]() can be evaluated (or estimated) for the nominal model. In particular, it is
notnecessary to re-identify the model, and the sensitivity and covariance matrices can be pre-computed off-line.
can be evaluated (or estimated) for the nominal model. In particular, it is
notnecessary to re-identify the model, and the sensitivity and covariance matrices can be pre-computed off-line.![]() have been affected by the change. Solutions for that are now described. How this relates to diagnostics is addressed afterwards.
have been affected by the change. Solutions for that are now described. How this relates to diagnostics is addressed afterwards.![]() have changed ?, can be addressed using either nuisance parameters elimination methods or a multiple hypotheses testing approach
. Here we only sketch two intuitively simple statistical nuisance
elimination techniques, which proceed by projection and rejection, respectively.
have changed ?, can be addressed using either nuisance parameters elimination methods or a multiple hypotheses testing approach
. Here we only sketch two intuitively simple statistical nuisance
elimination techniques, which proceed by projection and rejection, respectively.![]() is partitioned into an informative part and a nuisance part, and the sensitivity matrix
is partitioned into an informative part and a nuisance part, and the sensitivity matrix
![]() , the Fisher information matrix
, the Fisher information matrix
![]() and the normalized residual
and the normalized residual
![]() are partitioned accordingly
are partitioned accordingly![]()
![]() onto the subspace generated by the components
onto the subspace generated by the components
![]()
![]()
![]()
![]()
![]() 0,
0,
![]()
![]()
![]() is the partial residual (score). If
is the partial residual (score). If
![]()
![]()
![]()
![]()
![]()
![]()
![]() 0, with
0, with
![]()
![]()
![]() is the effective residual (score) resulting from the regression of the informative partial score
is the effective residual (score) resulting from the regression of the informative partial score
![]() over the nuisance partial score
over the nuisance partial score
![]() , and where the Schur complement
, and where the Schur complement
![]() is the associated Fisher information matrix. If
is the associated Fisher information matrix. If
![]()
![]() has to be monitored using a simple (black-box) model characterized by an identifiable parameter vector
has to be monitored using a simple (black-box) model characterized by an identifiable parameter vector
![]() . A typical example is the vibration monitoring problem in module
, for which complex finite elements models are often available but not
identifiable, whereas the small number of existing sensors calls for identifying only simplified input-output (black-box) representations. In such a situation, two different diagnosis
problems may arise, namely diagnosis in terms of the black-box parameter
. A typical example is the vibration monitoring problem in module
, for which complex finite elements models are often available but not
identifiable, whereas the small number of existing sensors calls for identifying only simplified input-output (black-box) representations. In such a situation, two different diagnosis
problems may arise, namely diagnosis in terms of the black-box parameter
![]() and diagnosis in terms of the parameter vector
and diagnosis in terms of the parameter vector
![]() of the underlying physical model.
of the underlying physical model.![]() , where
, where
![]() is the Jacobian matrix at
is the Jacobian matrix at
![]() 0of the application
0of the application
![]() , and to use the sensitivity test (
) for the components of the parameter vector
, and to use the sensitivity test (
) for the components of the parameter vector
![]() . Typically this results in the following type of directional test :
. Typically this results in the following type of directional test :![]()
![]() for the physical model may have a non negligible influence on such type of tests, according to the numerical conditioning of the Jacobian matrices
for the physical model may have a non negligible influence on such type of tests, according to the numerical conditioning of the Jacobian matrices
![]() .
.![]() of the state transition matrix
of the state transition matrix
![]()
![]() defined by :
defined by :![]()
![]()
![]() is the vector whose elements are the eigenvalues
is the vector whose elements are the eigenvalues
![]() ,
,
![]() is the matrix whose columns are the
is the matrix whose columns are the
![]() 's, and
vecis the column stacking operator.
's, and
vecis the column stacking operator.![]() and:
and:
![]() . Direct computations of the
. Direct computations of the
![]()

![]() . The state-transition matrix
. The state-transition matrix
![]() . The eigenstructure
. The eigenstructure
![]() then results from (
).
then results from (
).
![]() , and
, and
![]() and
and
![]() are as in (
). Whether a nominal parameter
are as in (
). Whether a nominal parameter
![]() 0fits a given output covariance sequence
(
0fits a given output covariance sequence
(
![]()
![]() 0, compute
0, compute
![]() using (
), and perform e.g. a singular value decomposition (SVD) of
using (
), and perform e.g. a singular value decomposition (SVD) of
![]() for extracting a matrix
for extracting a matrix
![]()
![]() 0. Then the characterization writes:
0. Then the characterization writes:![]()
![]() 0and a new sample
0and a new sample
![]() are available.For checking whether the data agree with
are available.For checking whether the data agree with
![]() 0, the idea is to compute the empirical Hankel matrix
0, the idea is to compute the empirical Hankel matrix
![]() :
:![]()
![]()
![]() be the actual parameter value for the system which generated the new data sample, and
be the actual parameter value for the system which generated the new data sample, and
![]() be the expectation when the actual system parameter is
be the expectation when the actual system parameter is
![]() . From (
), we know that
. From (
), we know that
![]()
![]() 0)has zero mean when no change occurs in
0)has zero mean when no change occurs in
![]() , and nonzero mean if a change occurs. Thus
, and nonzero mean if a change occurs. Thus
![]()
![]() 0)plays the role of a residual.
0)plays the role of a residual.![]() in (
), and for deriving the residual. Factorization (
) is also the key for :
in (
), and for deriving the residual. Factorization (
) is also the key for :