Scientific Foundations
General Overview
In the specification of computational systems, logics are generally used in one of two approaches. In the
computation-as-modelapproach, computations are encoded as mathematical structures, containing such items as nodes, transitions, and state. Logic is used in an external sense to make
statements
aboutthose structures. That is, computations are used as models for logical expressions. Intensional operators, such as the modals of temporal and dynamic logics or the triples of Hoare
logic, are often employed to express propositions about the change in state. This use of logic to represent and reason about computation is probably the oldest and most broadly successful use
of logic in computation.
The
computation-as-deductionapproach, uses directly pieces of logic's syntax (such as formulas, terms, types, and proofs) as elements of the specified computation. In this much more rarefied
setting, there are two rather different approaches to how computation is modeled.
The
proof normalizationapproach views the state of a computation as a proof term and the process of computing as normalization (know variously as
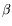 -reduction or cut-elimination). Functional programming can be explained using proof-normalization as its theoretical basis
-reduction or cut-elimination). Functional programming can be explained using proof-normalization as its theoretical basis
The
proof searchapproach views the state of a computation as a sequent (a structured collection of formulas) and the process of computing as the process of searching for a proof of a
sequent: the changes that take place in sequents capture the dynamics of computation. Logic programming can be explained using proof search as its theoretical basis
The divisions proposed above are informal and suggestive: such a classification is helpful in pointing out different sets of concerns represented by these two broad approaches (reductions,
confluence, etc, versus unification, backtracking search, etc). Of course, a real advance in computation logic might allow us merge or reorganize this classification.
Although type theory has been essentially designed to fill the gap between these two kinds of approaches, it appears that each system implementing type theory up to now only follows one of
the approaches. For example, the Coq system implementing the Calculus of Inductive Constructions (CIC) uses proof normalization while the Twelf system
The Parsifal team works on both the proof normalization and proof search approaches to the specification of computation.
Proof search in Type Theory
Cross-fertilizing ideas between the proof search approach and the proof normalization approach, Lengrand has interacted with the TypiCal (INRIA Saclay) and the

r2(INRIA Rocquencourt) project-teams.
In proof assistants based on the proof normalization approach, or Type Theory, it is a hard challenge to design and understand their proof search mechanisms. Based on ideas from
By doing so, we have helped improve the Coq system, by impacting the design of the new version of the tool's proof engine. One of these proof search mechanisms, known as
pattern unification, has again become a hot topic of Coq's design, after Lengrand's use of Coq to specify a particular algorithm has revealed a drastic need for this missing feature.
It also emerged from Lengrand's interaction with these project-teams, that bridging Type Theory with the proof theory developed at Parsifal confirms the need for more extensionality on the
functions programmed in Coq. Efforts to add such extensionality are ongoing.
A logic for reasoning about logic specifications
Coming up with the design of a logic that allows reasoning richly over relational specifications involving bindings in syntax has been a long standing problem, dating from at least the early
papers by McDowell and Miller
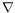 -quantifier that provided a significant improvement to the expressiveness of logic. Tiu then went on to enrich the possibilities of such a logic as well allowing for more “nominal”
effects to be captured
-quantifier that provided a significant improvement to the expressiveness of logic. Tiu then went on to enrich the possibilities of such a logic as well allowing for more “nominal”
effects to be captured
As described in Section
Focused proof systems
Several team members have continued their efforts to understand and apply focusing proof systems. Since Andreoli's first focused proof system for full linear logic
Baelde has also focused proof systems found in his PhD thesis
Deep Inference and Categorical Axiomatizations
Deep inference
One reason for using categories in proof theory is to give a precise algebraic meaning to the identity of proofs: two proofs are the same if and only if they give rise to the same morphism
in the category. Finding the right axioms for the identity of proofs for classical propositional logic has for long been thought to be impossible, due to “Joyal's Paradox”. For the same
reasons, it was believed for a long time that it it not possible to have proof nets for classical logic. Nonetheless, Lutz Straßburger and François Lamarche provided proof nets for classical
logic in
The following research problems are investigated by members of the Parsifal team:
Find deep inference system for richer logics. This is necessary for making the proof theoretic results of deep inference accessible to applications as they are described
in the previous sections of this report.
Investigate the possibility of focusing proofs in deep inference. As described before, focusing is a way to reduce the non-determinism in proof search. However, it is
well investigated only for the sequent calculus. In order to apply deep inference in proof search, we need to develop a theory of focusing for deep inference.
Use the results on deep inference to find new axiomatic description of categories of proofs for various logics. So far, this is well understood only for linear and
intuitionistic logics. Already for classical logic there is no common accepted notion of proof category. How logics like LINC can be given a categorical axiomatisation is completely
open.
Proof Nets and Combinatorial Characterization of Proofs
Proof nets are abstract (graph-like) presentations of proofs such that all "trivial rule permutations" are quotiented away. More generally, we investigate combinatoric objects and
correctness criteria for studying proofs independently from syntax. Ideally the notion of proof net should be independent from any syntactic formalism. But due to the almost absolute monopoly
of the sequent calculus, most notions of proof nets proposed in the past were formulated in terms of their relation to the sequent calculus. Consequently we could observe features like “boxes”
and explicit “contraction links”. The latter appeared not only in Girard's proof nets
The concept of deep inference allows to design entirely new kinds of proof nets. Recent work by Lamarche and Straßburger
Extend the work of Lamarche and Straßburger to larger fragments of linear logic, containing the additives, the exponentials, and the quantifiers.
Finding (for classical logic) a notion of proof nets that is deductive, i.e., can effectively be used for doing proof search. An important property of deductive proof
nets must be that the correctness can be checked in linear time. For the classical logic proof nets by Lamarche and Straßburger
A Systematic Approach to Cut Elimination
One of the main problems of proof theory is to prove cut elimination for new logics. Usually, a cut elimination proof is a tedious case analysis, and, in general, it is very fragile and not
modular
It is therefore an important research task, to find a more systematic approach to cut elimination proofs. That is to say, to find general guidelines that ensure the cut elimination property
for large classes of systems, in a similar way as it has been done for display logics
New Results
A logic for reasoning about logic specifications
David
Baelde
Andrew
Gacek
Dale
Miller
As described in Section
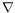 -quantification can be related to fixed point definitions and their associated induction and co-induction inference rules. Baelde has concentrated on proving focusing-style results that
are critical for proof automation and on a
minimal genericinterpretation of the
-quantification can be related to fixed point definitions and their associated induction and co-induction inference rules. Baelde has concentrated on proving focusing-style results that
are critical for proof automation and on a
minimal genericinterpretation of the
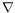 -quantifier. Gacek has concentrated on a
nominal genericinterpretation of the
-quantifier. Gacek has concentrated on a
nominal genericinterpretation of the
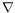 -quantifier. We now understand the difference between these logics: the nominal approach resembles much more closely the approach developed by Pitts
-quantifier. We now understand the difference between these logics: the nominal approach resembles much more closely the approach developed by Pitts
Full proofs of the important meta-theory results of the logic in Gacek's thesis have been submitted for publication
We have developed extensive examples of our this new logic: significant examples taken from the
 -calculus have been published in
-calculus have been published in
Two level of logic
Andrew
Gacek
Dale
Miller
Relational descriptions have been widely used in formalizing diverse computational notions, including, for example, operational semantics, typing, acceptance by non-deterministic machines,
etc. Such relational specifications can be faithfully captured by a (restricted) logical theory over relations. Such a
specification logiccan be picked so that it explicitly treats binding in object languages. Once such a logic is fixed, a natural next question is what devices should be used to prove
theorems about specifications written in it. Within the team, we have a second logic, called the
reasoning logic, to reason about provability in the first logic. To be adequate for this purpose, the reasoning logic should be able to completely encode the specification logic,
including notions of binding, such as quantifiers within formulas, for eigenvariables within sequents, and for abstractions within terms. To provide a natural treatment of these aspects, the
reasoning logic must encode binding structures as well as their associated notions of scope, free/bound variables, and capture-avoiding substitution. Furthermore, the reasoning logic should
possess strong mechanisms for constructing proofs by induction and co-induction.
Within the context of the Gacek's PhD thesis
 was present: this logic represents relations over
was present: this logic represents relations over
 -terms via definitions of atomic judgments, contains inference rules for induction and co-induction, and includes a special quantifier called
-terms via definitions of atomic judgments, contains inference rules for induction and co-induction, and includes a special quantifier called
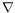 and a related generalization of equality over
and a related generalization of equality over
 -terms called
nominal abstraction. The interactive theorem prover Abella
-terms called
nominal abstraction. The interactive theorem prover Abella
 and supports this two-level logic approach to reasoning about computation. Gacek and others have now contributed a large number of interesting examples showing the utility of using this
two-level approach to reasoning: see the Abella web site for many examples. In particular, the POPLMark challenge problems 1a and 2a
and supports this two-level logic approach to reasoning about computation. Gacek and others have now contributed a large number of interesting examples showing the utility of using this
two-level approach to reasoning: see the Abella web site for many examples. In particular, the POPLMark challenge problems 1a and 2a
New insights into
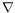 -quantification
David
Baelde
Andrew
Gacek
Dale
Miller
-quantification
David
Baelde
Andrew
Gacek
Dale
Miller
The team has been actively extending the scope of effectiveness
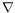 -quantification. As Tiu and Miller have shown in
-quantification. As Tiu and Miller have shown in
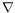 quantifier (developed in previous years within the team) provides a completely satisfactory treatment of binding structures in the
finite
quantifier (developed in previous years within the team) provides a completely satisfactory treatment of binding structures in the
finite
 -calculus. Moving this quantifier to treat infinite behaviors via induction and co-induction, required new advances in the underlying proof theory of
-calculus. Moving this quantifier to treat infinite behaviors via induction and co-induction, required new advances in the underlying proof theory of
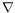 -quantification.
-quantification.
The team has explored two different approaches to this problem. David Baelde
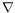 to interact properly with fixed points and their inference rules (namely, induction and co-induction). His logical approach allows for a rather careful and rigid understanding of scope
in the treatment of the meta-theory of logics and computational specifications.
to interact properly with fixed points and their inference rules (namely, induction and co-induction). His logical approach allows for a rather careful and rigid understanding of scope
in the treatment of the meta-theory of logics and computational specifications.
Another angle has been developed as a result of our close international collaborations. Alwen Tiu, now at the Australian National University, has developed a logic, called
 which extends the earlier, “minimal” approach by introducing the structural rules of strengthening and exchange into the context of generic variables. As a result, the behavior of
bindings becomes much more like the behavior of names more generally, while still maintaining much of the status as being binders. In combination with our close colleagues at the University of
Minnesota, we have extended this work to include a new definitional principle, called
nabla-in-the-head, that strengthens our ability to declaratively describe the structure of contexts and proof invariants. This new definitional principle was first presented in
which extends the earlier, “minimal” approach by introducing the structural rules of strengthening and exchange into the context of generic variables. As a result, the behavior of
bindings becomes much more like the behavior of names more generally, while still maintaining much of the status as being binders. In combination with our close colleagues at the University of
Minnesota, we have extended this work to include a new definitional principle, called
nabla-in-the-head, that strengthens our ability to declaratively describe the structure of contexts and proof invariants. This new definitional principle was first presented in
Foundational aspects of focusing proof systems
David
Baelde
Kaustuv
Chaudhuri
Dale
Miller
Alexis
Saurin
Since focusing proof systems seem to be behind much of our computational logic framework, the team has spent some energies developing further some foundational aspects of this approach to
proof systems.
Chuck Liang and Miller have recently finished the paper
Given the team's ambitious to automate logics that require induction and co-induction, we have also looked in detail at the proof theory of fixed points. In particular, David Baelde's recent
PhD thesis
Alexis Saurin's recent PhD
A particular outcome of our work on focused proof search is the use of
maximally multifocused proofsto help provide sequent calculus proofs a canonicity. In particular, Chaudhuri, Miller, and Saurin have shown in
A completely symmetric approach to proof and refutation
Olivier
Delande
Dale
Miller
Alexis
Saurin
A couple of years ago, Miller and Saurin proposed a neutral approach to proof and refutation. The goal was to describe an entirely neutral setting where a step in a “proof search” could be
seen as a step in either building a proof of a formula or a proof of its negation. The early work was limited to essentially a simple generalization to additive logic. Delande was able to
generalize that work to capture multiplicative connectives as well. His thesis
The paper
Bor a refutation of
B(
i.e., a proof of
¬
B) can be carried out simultaneously: in contrast, the usual approach in automated deduction views proving
Bor proving
¬
Bas two, possibly unrelated, activities. Their approach to proof and refutation is described as a two-player game in which each player follows the same rules. A
winning strategy translates to a proof of the formula and a counter-winning strategy translates to a refutation of the formula. The game is described for multiplicative and additive linear
logic (MALL). A game theoretic treatment of the multiplicative connectives is intricate and involves two important ingredients. First, labeled graph structures are used to represent positions
in a game and, second, the game playing must deal with the failure of a given player and with an appropriate resumption of play. This latter ingredient accounts for the fact that neither player
might win (that is, neither
Bnor
¬
Bmight be provable).
Subexponentials
Dale
Miller
Vivek
Nigam
The inference rules of a logic define a logical connective in a canonical fashion if the following test is passed: assume that there are two copies of a logical connective, say a red and
blue copy, and assume that both of these connectives have the same introduction rules. If it is possible to prove that the red and blue versions are equivalent within the extended proof system,
then we say that the connective is defined canonically. In linear logic, all connectives are canonical in this sense except for the exponentials (!, ?). That is, it is possible to have many
exponentials and they do not need to all support weakening and contraction but some subsets of these structural rules. Since they do not need to provide all structural rules, we have called
these not exponentials but
subexponentials
Proof theory does not provide canonical solutions for many things in computational logic: for example, the domain of first-order quantification is seldom addressed by proof theory as well as
the exact nature of worlds within, say, Kripke models. These non-canonical aspects of logic provide, however, important opportunities for computer scientists to attach structures that they need
to logic. Since the exponentials are not canonical, maybe there are possible exploitations of such non-canonical exponentials in computer science. Nigam and Miller have provided a partial
answer to this question. In particular, they have shown that rich forms of multiset computation can be supported using subexponentials
A framework for proof systems
Vivek
Nigam
Dale
Miller
In earlier work by Pimentel and Miller
Modular Systems for Modal Logics
Lutz
Straßburger
There are modal logics like S4 or K, for which it is rather straightforward to provide a cut-free sequent system, and there are others, like S5 for which this is difficult or impossible. We
(in a joint work with Kai Brünnler, Univ. Bern) used “nested sequents”
Generic cut-elimination for Substructural Logics
Lutz
Straßburger
We were able (in a joint work with Agata Ciabattoni, TU Wien, and Kazushige Terui, Kyoto University) to make further progress in the development of a systematic and algebraic proof theory
for nonclassical logics. Continuing the work of
P3'of the hierarchy into inference rules in multiple-conclusion (hyper)sequent calculi, which enjoy cut-elimination under a certain condition. This allows a systematic treatment of logics
which could not be dealt with in previous approaches. Our method also works as a heuristic principle for finding appropriate rules for axioms located at levels higher than
P3'. The work is published in
A Kleene Theorem for Forest Languages
Lutz
Straßburger
Kleene's theorem on the coincidence of the rational and the recognizable languages in a free monoid
Computation with meta-variables
Stéphane
Lengrand
Meta-variables are central in proof search mechanisms to represent incomplete proofs and incomplete objects. They are used in almost all implementations of proof-related software, yet their
meta-theory remains less explored than that of complete proofs and objects such as in the
 -calculus.
-calculus.
In 2009, Stéphane Lengrand and Jamie Murdoch Gabbay have published in
This proposal, extending the
 calculus with a particular kind of meta-variables originating from nominal logic, is more sparing than previous approaches like
Higher-Order Abstract Syntax, which explicitly represents
all potentialdependencies between incomplete objects (this leads to computational inefficiencies as potential dependencies that are not effectively used still incur a computational
cost).
calculus with a particular kind of meta-variables originating from nominal logic, is more sparing than previous approaches like
Higher-Order Abstract Syntax, which explicitly represents
all potentialdependencies between incomplete objects (this leads to computational inefficiencies as potential dependencies that are not effectively used still incur a computational
cost).
Lengrand and Gabbay's proposal is only a first step, as it does not have a neat theory of normal forms (i.e. output values). A more complete version of such a
 -calculus, with incomplete objects and arbitrary binding dependencies but also with better normalization properties, has been in development since.
-calculus, with incomplete objects and arbitrary binding dependencies but also with better normalization properties, has been in development since.
Encoding constrained transition systems
Kaustuv
Chaudhuri
Joëlle
Despeyroux
Joëlle Despeyroux and Kaustuv Chaudhuri have given an encoding of the synchronous stochastic
 -calculus in a hybrid extension of intuitionistic linear logic (called HyLL). Precisely, they have shown that focused partial sequent derivations in the encoding are in bijection with
stochastic traces. The modal worlds are used to represent the rates of stochastic interactions, and the connectives of hybrid logic are used to represent the constraints in the stochastic
transition rules. These results have been submitted to a journal
-calculus in a hybrid extension of intuitionistic linear logic (called HyLL). Precisely, they have shown that focused partial sequent derivations in the encoding are in bijection with
stochastic traces. The modal worlds are used to represent the rates of stochastic interactions, and the connectives of hybrid logic are used to represent the constraints in the stochastic
transition rules. These results have been submitted to a journal
One of the most successful applications of the stochastic
 -calculus has been in representing signal transduction networks in cellular biology. An interesting application of this work would therefore be the direct representations of biological
processes in HyLL, the original motivation for this line of investigation. Furthermore, other stochastic systems can, at least in principle, be similarly encoded in HyLL, giving us the
linguistic ability to compare and combine systems represented using different stochastic formalisms.
-calculus has been in representing signal transduction networks in cellular biology. An interesting application of this work would therefore be the direct representations of biological
processes in HyLL, the original motivation for this line of investigation. Furthermore, other stochastic systems can, at least in principle, be similarly encoded in HyLL, giving us the
linguistic ability to compare and combine systems represented using different stochastic formalisms.
Cut-elimination in classical logic
Stefan
Hetzl
A central research topic of the team are the connections between proof theory and computation. A proof-theoretic method which is often used for modeling computational systems is
cut-elimination. The computational aspects of this procedure are rather well understood for intuitionistic and linear logic while the situation in classical logic is less satisfactory.
![]() -calculus), concurrent computation (e.g.,
-calculus), concurrent computation (e.g.,
![]() -calculus), interactive computations (e.g., games), and biological systems.
-calculus), interactive computations (e.g., games), and biological systems.