Effective 3D global visibility, theory and applications
Guillaume
Batog
Hazel
Everett
Xavier
Goaoc
Sylvain
Lazard
Sylvain
Petitjean
Linqiao
Zhang
In recent years, our activity in the area of 3D visibility focused on three main directions: (i) the computation and complexity analysis of the
3D visibility complex,(ii) the computation and complexity analysis of the boundary of shadows cast by area light sources, and (iii) the study of some fundamental questions in geometric
transversal theory.
The 3D visibility complex is a partition of the space of rays according to visibility. The questions we consider are two-fold. On one hand, we study its size, both experimentally and
theoretically. This size is reflected in the number of unobstructed line segments tangent to four objects of the scene; while this number can be
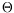 (
(
n4)in unstructured scenes, its behavior for more
realisticinput is still not understood. On the other hand, we work on the computation of the
3D Visibility skeleton,a substructure of the visibility complex. A few years ago we presented a worst-case near-optimal sweep-plane algorithm for computing this structure in a
restrictive setting
Shadows play a central role in human perception and a wide variety of approaches have been considered for simulating and rendering them. Unfortunately, computing realistic shadows
efficiently is a very difficult problem, particularly in the case of non-point light sources, due to the complicated internal structure that such shadows may have. The only current solution for
that problem goes through a discretization of area light sources by many point light sources; shadows cannot be certified with this approach and their structure is lost. As a first
approximation, one can compute the main shadow boundaries, that is the boundary between the regions in full-light, penumbra, and umbra. Specifically, a point is in the umbra if it does not see
any part of any light source; it is in full light if it sees entirely all the light sources; otherwise, it is in the penumbra. These boundaries are traced out by one-parameter families of
segments that belong to the 3D Visibility skeleton. On one hand, we try to estimate the complexity of these shadow boundaries, both in theory and in practice. On the other hand, we work on
applying our methods for computing the visibility skeleton to this particular problem.
The study of fundamental properties of sets of lines, that is,
line geometry,underlies many algorithmic questions including 3D visibility computations. A few years ago, we generalized Helly's classical theorem to sets of line transversals to
disjoint unit balls in

Visibility complex and skeleton
This year, our PhD student Linqiao Zhang, co-supervised with S. Whitesides at McGill University, defended her Ph.D. thesis entitled
On the three-dimensional visibility skeleton: implementation and analysis
We also obtained a new result on the complexity of the set free lines and free lines segments tangent to balls in 3D. In particular, we proved that, in the presence of
ndisjoint unit balls, the set of free line segment, that is the so-called visibility complex, has complexity
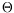 (
(
n4). This result is very surprising because it was natural to conjecture that the visibility complex of fat objects of similar size had a lower worst-case complexity than
that for thin triangles. Our result settles negatively this conjecture, and shows exactly the opposite, that is, that fatness and similarity, alone, do not reduce the worst-case complexity of
that structure. This result was submitted to the
Symposium on Computational Geometryin December 2009
In the context of the PhD thesis of Guillaume Batog, we are working on an invariant-based method for designing efficient evaluation strategies for predicates. In a nutshell, the idea is to
find a group action on the input space of a predicate with two properties: it has few orbits, and any two inputs in the same orbit are equivalent for the predicate. The invariants of that
action are known, under certain conditions, to distinguish the various orbits, and can then be used to decide the predicate. This year, we unfolded this approach for predicates on line
systems that arise in visibility computations, for instance deciding the number of lines intersecting four given lines. A communication is in preparation.
Shadow computations
We published this year two results on the umbra and penumbra cast by non-trivial light sources.
First, we published the first non-trivial bounds on the size of the umbra region. These result show that the umbra can be surprisingly complicated, even in the presence of disjoint fat
obstacles; for instance, we proved that the umbra cast on a plane by a segment light source in the presence of two fat polytopes of size
n, can have up to
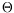 (
(
n)connected components in the worst case. These results were published in the journal
Computational Geometry, Theory and Applications
We also developed, over the last years, a new method for the exact computation of shadow boundaries. The associated prototype software is, up to our knowledge, the first implementation
that computes exactly such shadow boundaries of polygonal light sources in the presence of polyhedral obstacles for nontrivial scenes (
e.g.,50 polytopes with 1 500 vertices). Using this implementation, we observed experimentally a significant gap between the size of the visibility skeleton and the, much smaller,
complexity of the shadow boundaries. We presented these results at the
European Workshop on Computational Geometry
Pinning and line transversals
In the last few years, we strived to understand the combinatorial properties of so-called
isolated line transversals,also called
pinnings: these lines meet every member in a family of objects, but they lose this property when subject to any arbitrarily small perturbation. We obtained a
basis theoremwhen the objects are disjoint balls in
 in 2006
in 2006
 contains a pinning of size at most
2
contains a pinning of size at most
2
d-1. We strengthened this result in three ways. First, we proved that this constant,
2
d-1,is best possible for all dimension, a result obtained in 2008. In 2009, we presented this result at the
Eurocombconference
 . This year, we added to this extension a complete description of minimal pinning configurations; these results were submitted to the
Symposium on Computational Geometryin December 2009
. This year, we added to this extension a complete description of minimal pinning configurations; these results were submitted to the
Symposium on Computational Geometryin December 2009
An order in which a line can intersect a collection of geometric objects is called a
geometric permutationof that collection. When the objects are disjoint balls, the geometric permutations count the connected components of the space of line transversals ; more
generally, it gives a lower bound on its topological complexity. Substantial effort has been devoted to understanding how the geometry of the objects constrains the number of geometric
permutations; the asymptotic behavior of the maximum number of geometric permutations of
ndisjoint convex sets in
 has remained an open problem for two decades. We have been working on a new approach to this question. The idea is to analyze how the knowledge of a bound for constant-size problems
(say, knowing that the maximum number of geometric permutations for 10 objects is at most 24) helps bounding the asymptotic behavior for
has remained an open problem for two decades. We have been working on a new approach to this question. The idea is to analyze how the knowledge of a bound for constant-size problems
(say, knowing that the maximum number of geometric permutations for 10 objects is at most 24) helps bounding the asymptotic behavior for
nobjects. This year, we made a first step in this direction: we delineated the main growth rates (constant, polynomial, exponential) through a generalization of Sauer's Lemma for
shatter functionsof set systems.
Certified geometric computing for curves and surfaces
Jinsan
Cheng
Laurent
Dupont
Hazel
Everett
Sylvain
Lazard
Luis
Peñaranda
Maria
Pentcheva
Sylvain
Petitjean
Marc
Pouget
George
Tzoumas
Voronoi diagram of polyhedra in 3D
We are working on the problem of computing the medial axis or Voronoi diagram of polyhedra in 3D. These structures are largely used in applications; the medial axis is, for instance, a way
of representing a shape by its topological skeleton. Such a diagram is a partition of space into cells, each of which consists of the points closest to one particular object than to any
other. Moreover, the set of points equidistant to two lines (or to a line and a point) is a quadric and the set of points equidistant to three lines is the intersection of two quadrics. While
such structures are well-understood in the plane and for simple situations in higher dimensions (e.g. for sets of points), a lot remains to be done; for example, there is no working solution
for computing exactly the medial axis of a polyhedron.
We started a few years ago by considering the Voronoi diagram of lines and we finally published this year, in the journal
Discrete and Computational Geometry,some very nice results characterizing the topology of the Voronoi diagrams of three lines
We have worked during the last two years on the problem of extending these results to the case of three lines in arbitrary positions providing the first complete characterization of the
Voronoi diagram of any three lines. Preliminary results were presented this year at the European Workshop on Computational Geometry
Adjacency graph of an arrangement of integer quadrics
We have presented, a couple years ago, a complete, exact and efficient algorithm and its implementation for computing the adjacency graph of an arrangement of quadrics with integer
coefficients
Algebraic tools for geometric computing
In computational geometry, many problems lead to standard, though difficult, algebraic questions such as computing the real roots of a system of equations, computing the sign of a
polynomial at the roots of a system, or determining the dimension of a set of solutions. Our goal is two-fold. First, we want to make state-of-the-art algebraic software more accessible to
the computational geometry community, in particular, through the computational geometric library CGAL. Second, our goal is to demonstrate to which extent such state-of-the-art certified
algebraic root-finding systems can be used in geometric algorithms to obtain certified constructions involving curved objects without hindering performance. We have presented some results in
these two directions at the 8th International Symposium on Experimental Algorithms, SEA'09
Topology and geometry of algebraic curves:
Isotop
We worked over the last years on the problem of computing, in a certified way, the topology of algebraic curves, that is, computing an arrangement of polylines isotopic to the input curve.
The objective here is to compute efficiently and in a certified way arrangements of algebraic curves. A necessary key step is to compute the topology of any given curve. Moreover, geometric
information, such as the position of singular and critical points, is also mandatory for computing arrangements of several curves using a sweep-line algorithm. A difficulty is to compute
efficiently this information for the given coordinate system even if the curve is not in generic position; previous practical approaches shear back and forth the coordinate system, which is
time consuming. In addition, costly computations with polynomials whose coefficients are algebraic should be avoided. We have recently presented an algorithm that incorporates several
improvements over previous methods and overcome these difficulties. In particular, our approach does not require generic position nor shearing. This work has been presented this year at the
25th annual Symposium on Computational Geometry
Constant-complexity geometric problems and algebraic invariants
We have continued revisiting some key constant-complexity geometric problems with a view to better understand their degenerate instances and the geometric predicates underlying their
detection. For that, we mostly rely on classical tools, in particular (classical) algebraic invariant century, which was perceived as a bridge between geometry and algebra by the
mathematicians of the 19th century (culminating with Klein's Erlangen Program, and the view of geometry as the study of the properties of a space invariant under the action of a group of
transformations). Last year, we studied the relative position of two plane projective conics and showed that it can be characterized by predicates of bidegree at most
(6, 6)in the coefficients of the input conics
Bounded-curvature path planning
We studied the problem of computing shortest paths of bounded curvature that visits a sequence of
npoints in order. This problem, which has been open for about 15 years, is crucial for path planning of car-like robots in the presence of polygonal obstacles. We proved that, under
some conditions, this problem reduces to optimizing a convex function over a convex
n-dimensional domain. This result reveals a fundamental property of curvature-constrained paths among polygonal obstacles, and it provides the first efficient solution for this
long-standing problem. This result has been submitted to the
Symposium on Computational Geometryin December 2009
Embedding geometric structures
This year, we started work on the problem of embedding geometric objects on a grid of
 . Essentially all industrial applications take, as input, models defined with a fixed-precision floating-point arithmetic, typically doubles. As a consequence, geometric objects
constructed using exact arithmetic must be embedded on a fixed-precision grid before they can be used as input in other software. More precisely, the problem is, given a geometric object, to
find a similar object representable with fixed-precision floating-point arithmetic, where similar means topologically equivalent, close according to some distance function, etc. We started
working on the problem of rounding polyhedral subdivisions on a grid of
. Essentially all industrial applications take, as input, models defined with a fixed-precision floating-point arithmetic, typically doubles. As a consequence, geometric objects
constructed using exact arithmetic must be embedded on a fixed-precision grid before they can be used as input in other software. More precisely, the problem is, given a geometric object, to
find a similar object representable with fixed-precision floating-point arithmetic, where similar means topologically equivalent, close according to some distance function, etc. We started
working on the problem of rounding polyhedral subdivisions on a grid of
 , where the only known method, due to Fortune, induces a blow-up in the complexity that is inacceptable in practice. We worked so far on the simpler problem of embedding convex
polyhedra. We also showed negative results that, even in the plane, convex polygons cannot be rounded while conserving both convexity and proximity of the rounded vertices. This project is
joint work with Mark de Berg (Eindhoven University), Dan Halperin (Tel Aviv University) and Olivier Devillers (Geometrica, INRIA).
, where the only known method, due to Fortune, induces a blow-up in the complexity that is inacceptable in practice. We worked so far on the simpler problem of embedding convex
polyhedra. We also showed negative results that, even in the plane, convex polygons cannot be rounded while conserving both convexity and proximity of the rounded vertices. This project is
joint work with Mark de Berg (Eindhoven University), Dan Halperin (Tel Aviv University) and Olivier Devillers (Geometrica, INRIA).
Other results
We initiated a collaboration with O. Devillers (INRIA, Sophia-Antipolis) and D. Attali (Gipsa, Grenoble) on
smoothed complexityanalysis of geometric data structures. In many cases, the worst-case complexity analysis poorly represents the practical performances of algorithms or data structures.
The smoothed complexity, which aims at supplementing this gap, is defined as the maximum over the inputs of the expected complexity over small perturbations of that input. We obtained some
preliminary results on the smoothed number of extreme points of a convex point set subject to random noise; we submitted these results to the
Symposium on Computational Geometryin December
We completed some research on farthest-site Voronoi diagrams of polygonal sites of total complexity
n. We proved that the combinatorial complexity of such diagrams is
O(
n), and we presented an
O(
nlog
3n)time algorithm to compute it. These results were submitted to the journal
Transactions on Algorithms
One of our earlier results on computational topology was accepted this year in the journal
Computational Geometry, Theory and Applications
Finally, two of our earlier results in graph drawing were also accepted or published this year in the journal of
Discrete and Computational Geometry
nvertices can be point-set embedded with at most one bend per edge on a given set of
npoints in the plane. An implication of this result is that any number of planar graphs admit a simultaneous embedding without mapping with at most one bend per edge.
![]() where a prototype of a 3D computer model is constructed by first decomposing the model into layers and then manufacturing separately each layer, typically out of wood of standard
thickness (e.g. 1 cm), with a three-axis CNC (Computer Numerical Controls) milling machine. The layers are then assembled together to form the object. The Stratoconception
where a prototype of a 3D computer model is constructed by first decomposing the model into layers and then manufacturing separately each layer, typically out of wood of standard
thickness (e.g. 1 cm), with a three-axis CNC (Computer Numerical Controls) milling machine. The layers are then assembled together to form the object. The Stratoconception
![]() technique is cheap and allows fast prototyping of large models.
technique is cheap and allows fast prototyping of large models.