Parametric estimation may often be formalized as follows:
y=
F(
x,
![]() ) +
) +
n,
where:
the measured signal
yis a functional
Fof the "true" signal
x, which depends on a set
![]() of parameters,
of parameters,
nis a noise corrupting the observation.
Finding a "good" approximation of the components of
![]() has been the subject of a huge literature in various
fields of applied mathematics. Most of those researches have
been done in a probabilistic setting, which necessitates a
good knowledge of the statistical properties of
has been the subject of a huge literature in various
fields of applied mathematics. Most of those researches have
been done in a probabilistic setting, which necessitates a
good knowledge of the statistical properties of
n. Our project is devoted to a new standpoint which
does not require this knowledge and which is based on the
following tools, which are of algebraic flavor:
differential algebra
module theory, i.e., linear algebra over rings which are not necessarily commutative;
operational calculus which was the
most classical tool among control and mechanical
engineers
![]() is not.
is not.
In most problems appearing in linear control as well as in signal processing, the unknown parameters are linearly identifiable: standard elimination procedures yield the following matrix equation
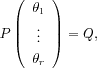
where:
![]()
i,
1
![]()
i
![]()
r, represents an unknown
parameter,
Pis a
r×
rsquare matrix and
Qis a
r×1column matrix,
the entries of
Pand
Qare finite linear combinations of terms of the
form
![]() ,
,
![]() ,
,
![]()
![]() 0, where
0, where
![]() is an input or output signal,
is an input or output signal,
the matrix
Pis
genericallyinvertible, i.e.,
det(
P)
![]() 0.
0.
With noisy measurements, the equation ( ) becomes:
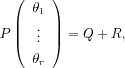
where
Ris a
r×1column matrix, whose entries
are finite linear combination of terms of the form
![]() , where
, where
![]() is a perturbation or a noise.
is a perturbation or a noise.
A perturbation
![]() is said to be
structuredif, and only if, it is annihilated by a
linear differential operator of the form
is said to be
structuredif, and only if, it is annihilated by a
linear differential operator of the form
![]() , where
, where
ak(
t)is a rational function
of
t, i.e.,
![]() . Note that many classical perturbations like a
constant bias are annihilated by such an operator. An
unstructurednoise cannot be annihilated by a
non-zero differential operator.
. Note that many classical perturbations like a
constant bias are annihilated by such an operator. An
unstructurednoise cannot be annihilated by a
non-zero differential operator.
By well-known properties of the non-commutative ring
of differential operators, we can multiply both sides of
equation (
) by a suitable differential
operator
![]() such that equation (
) becomes:
such that equation (
) becomes:
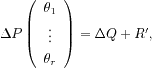
where the entries of the
r×1column matrix
R'are unstructured noises.
Unstructured noises are usually dealt with stochastic processes like white Gaussian noises. They are considered here as highly fluctuating phenomena, which may therefore be attenuated vialow pass filters. Note that no precise knowledge of the statistical properties of the noises is required.
Although the previous noise attenuation
The time derivatives of the input and output signals appearing in equations ( ), ( ), ( ) can be suppressed in the two following ways which might be combined:
integrate both sides of the equation a sufficient number of times,
take the convolution product of both sides by a suitable low pass filter.
The numerical values of the unknown parameters
![]() can be obtained by integrating both sides of the
modified equation (
) during a very short time
interval.
can be obtained by integrating both sides of the
modified equation (
) during a very short time
interval.
Let us illustrate on a very basic example, the grounding ideas of the ALIEN approach, based on algebra. For this, consider the first order, linear system:
![]()
where
ais an unknown parameter to be identified and
![]() 0is an unknown, constant perturbation. With the
notations of operational calculus and
0is an unknown, constant perturbation. With the
notations of operational calculus and
y0=
y(0), equation (
) reads:
![]()
where
![]() represents Laplace transform.
represents Laplace transform.
In order to eliminate the term
![]() 0, multiply first the two hand-sides of this equation
by
0, multiply first the two hand-sides of this equation
by
sand, then, take their derivatives with respect to
s:
![]()
![]()
Recall that
![]() corresponds to
-
corresponds to
-
t
y(
t). Assume
y0= 0for simplicity's sake
y0![]() 0one has to take above derivatives of
order 2 with respect to
0one has to take above derivatives of
order 2 with respect to
s, in order to eliminate the initial
condition.![]() >0,
>0,
![]()
For
![]() = 3, we
obtained the estimated value
= 3, we
obtained the estimated value
a:
![]()
Since
T>0can be very small,
estimation
via(
) is very fast.
Note that equation (
) represents an on-line
algorithm that only involves two kinds of operations on
uand
y:(1) multiplications by
t, and (2) integrations over a pre-selected time
interval.
If we now consider an additional noise, of zero mean, in ( ), say:
![]()
it will be considered as fast
fluctuating signal. The order
![]() in (
) determines the order of
iterations in the integrals (3 integrals in (
)). Those iterated integrals
are low-pass filters which are attenuating the
fluctuations.
in (
) determines the order of
iterations in the integrals (3 integrals in (
)). Those iterated integrals
are low-pass filters which are attenuating the
fluctuations.
This example, even simple, clearly demonstrates how ALIEN's techniques proceed:
they are algebraic: operations on
s-functions;
they are non-asymptotic:
parameter
ais obtained from (
) in finite time;
they are deterministic: no knowledge
of the statistical properties of the noise
nis required.
Consider the first order, linear system with constant
input delay
![]()
Here we use a distributional-like notation where
![]() denotes the Dirac impulse and
denotes the Dirac impulse and
His its integral, i.e., the Heaviside function (unit
step)
Hand the integration operator. To be rigorous, the
iterated integration (
ktimes) corresponds, in the operational domain, to a
division by
sk, whereas the convolution with
H(
ktimes) corresponds to a division by
sk/(
k-1)!. For
k= 0, there is no difference and
H*
yrealizes the integration of
y. More generally, since we will always apply these
operations to complete equations (left- and right-hand
sides), the factor
(
k-1)!makes no
difference.ais known. The parameter to be identified is now the
delay
![]() . As previously,
. As previously,
![]() 0is a constant perturbation,
0is a constant perturbation,
a,
b, and
![]() are constant parameters. Consider also a step
input
are constant parameters. Consider also a step
input
u=
u0H. A first order derivation
yields:
![]()
where
![]() denotes the delayed Dirac impulse and
denotes the delayed Dirac impulse and
![]() , of order 1 and support
{0}, contains the contributions
of the initial conditions. According to Schwartz theorem,
multiplication by a function
, of order 1 and support
{0}, contains the contributions
of the initial conditions. According to Schwartz theorem,
multiplication by a function
![]() such that
such that
![]() (0) =
(0) =
![]() '(0) = 0,
'(0) = 0,
![]() (
(
![]() ) =
0yields interesting simplifications. For instance,
choosing
) =
0yields interesting simplifications. For instance,
choosing
![]() (
(
t) =
t3-
![]()
t2leads to the following equalities (to be
understood in the distributional framework):
![]()
The delay
![]() becomes available from
becomes available from
k![]() 1successive integrations (represented
by the operator
1successive integrations (represented
by the operator
H), as follows:
![]()
where the
wiare defined, using the notation
zi=
tiy, by:
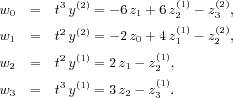
These coefficients show that
k![]() 2integrations are avoiding any
derivation in the delay identification.
2integrations are avoiding any
derivation in the delay identification.
Figure
gives a numerical simulation
with
k= 2integrations and
a= 2,
b= 1,
![]() =
0.6,
=
0.6,
y(0) = 0.3,
![]() 0= 2,
0= 2,
u0= 1. Due to the non identifiability over
(0,
![]() ),
the delay
),
the delay
![]() is set to zero until the numerator or the
denominator in the right hand side of (
) reaches a significant nonzero
value.
is set to zero until the numerator or the
denominator in the right hand side of (
) reaches a significant nonzero
value.
Again, note the realization algorithm (
) involves two kinds of
operators: (1) integrations and
(2) multiplications by
t.
It relies on the measurement of
yand on the knowledge of
a. If
ais also unknown, the same approach can be utilized
for a simultaneous identification of
aand
![]() . The following relation is derived from (
):
. The following relation is derived from (
):
![]() (
(
Hkw1) +
a![]() (
(
Hkw2)-
a(
Hkw3) =
Hkw0,
and a linear system with unknown
parameters
(
![]() ,
,
a
![]() ,
,
a)is obtained by using different
integration orders:

The resulting numerical simulations are shown in
Figure
. For identifiability reasons,
the obtained linear system may be not consistent for
t<
![]() .
.
Numerical differentiation, i.e., determining the time derivatives of various orders of a noisy time signal, is an important but difficult ill-posed theoretical problem. This fundamental issue has attracted a lot of attention in many fields of engineering and applied mathematics (see, e.g. in the recent control literature , , , , , , and the references therein). A common way of estimating the derivatives of a signal is to resort to a least squares fitting and then take the derivatives of the resulting function. In , , this problem was revised through our algebraic approach. The approach can be briefly explained as follows:
The coefficients of a polynomial time
function are linearly identifiable. Their estimation can
therefore be achieved as above. Indeed, consider the
real-valued polynomial function
![]() ,
,
t![]() 0, of degree
0, of degree
N. Rewrite it in the well known notations of
operational calculus:
![]()
Here, we use
![]() , which corresponds in the time domain to the
multiplication by
-
, which corresponds in the time domain to the
multiplication by
-
t. Multiply both sides by
![]() ,
,
![]() . The quantities
. The quantities
![]() ,
,
![]() are given by the triangular system of linear
equations:
are given by the triangular system of linear
equations:
![]()
The time derivatives, i.e.,
![]() ,
,
![]() ,
0
,
0
![]()
![]()
![]()
N, are removed by multiplying
both sides of Equation (
) by
![]() ,
,
![]() .
.
For an arbitrary analytic time
function, apply the preceding calculations to a suitable
truncated Taylor expansion. Consider a real-valued
analytic time function defined by the convergent power
series
![]() , where
0
, where
0
![]()
t<
![]() .
Approximate
.
Approximate
x(
t)in the interval
(0,
![]() ),
0<
),
0<
![]()
![]()
![]() ,
by its truncated Taylor expansion
,
by its truncated Taylor expansion
![]() of order
of order
N. Introduce the operational analogue of
x(
t), i.e.,
![]() . Denote by
. Denote by
![]() ,
0
,
0
![]()
![]()
![]()
N, the numerical estimate of
![]() , which is obtained by replacing
, which is obtained by replacing
XN(
s)by
X(
s)in Eq. (
). It can be shown
that a good estimate is
obtained in this way.
Thus, using elementary differential algebraic operations,
we derive explicit formulae yielding point-wise derivative
estimation for each given order. Interesting enough, it turns
out that the Jacobi orthogonal polynomials
are inherently connected with the
developed algebraic numerical differentiators. A
least-squares interpretation then naturally follows
,
and this leads to a key result:
the algebraic numerical differentiation is as efficient as an
appropriately chosen time delay. Though, such a delay may not
be tolerable in some real-time applications. Moreover,
instability generally occurs when introducing delayed signals
in a control loop. Note however that since the delay is known
a priori, it is always possible to derive a control
law which compensates for its effects (see
). A second key feature of the
algebraic numerical differentiators is its very low
complexity which allows for a real-time implementation.
Indeed, the
nthorder derivative estimate (that can be directly
managed for
n![]() 2,
without using
2,
without using
ncascaded estimators) is expressed as the output of the
linear time-invariant filter, with finite support impulse
response
![]() . Implementing such a stable and causal filter is easy
and simple. This is achieved either in continuous-time or in
discrete-time when only discrete-time samples of the
observation are available. In the latter case, we obtain a
tapped delay line digital filter by considering any numerical
integration method with equally-spaced abscissas.
. Implementing such a stable and causal filter is easy
and simple. This is achieved either in continuous-time or in
discrete-time when only discrete-time samples of the
observation are available. In the latter case, we obtain a
tapped delay line digital filter by considering any numerical
integration method with equally-spaced abscissas.