Scientific Foundations
Dynamic non-regular systems
Dynamical systems (we limit ourselves to
finite-dimensional ones) are said to be
non-regularwhenever some nonsmoothness of the state
arises. This nonsmoothness may have various roots: for
example some outer impulse, entailing so-called
differential equations with measure. An important
class of such systems can be described by the complementarity
system
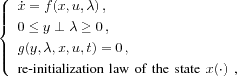
where
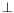 denotes orthogonality;
denotes orthogonality;
uis a control input. Now (
Hybrid systems: it is in fact natural
to consider that (
yi= 0or
yi>0(
yibeing a component of the vector
y). In some cases, passing from one mode to the
other implies a jump in the state
x; then the continuous dynamics in (
Differential inclusions:
0
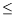
y
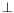

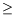 0is equivalent to
-
0is equivalent to
-

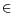 N
N
K(
y), where
Kis the nonnegative orthant and
N
K(
y)denotes the normal cone to
Kat
y. Then it is not difficult to reformulate (
Dynamic variational inequalities: such
a formalism reads as
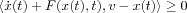 for all
for all
v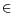
Kand
x(
t)
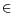
K, where
Kis a nonempty closed convex set. When
Kis a polyhedron, then this can also be written as
a complementarity system as in (
Thus, the 2nd and 3rd lines in (
x. There are several other formalisms which are quite
related to complementarity. A tutorial-survey paper has been
published
Nonsmooth optimization
Here we are dealing with the minimization of a function
f(say over the whole space
R
n), whose derivatives are discontinuous. A
typical situation is when
fcomes from dualization, if the primal problem is not
strictly convex – for example a large-scale linear program –
or even nonconvex – for example a combinatorial optimization
problem. Also important is the case of spectral functions,
where
f(
x) =
F(
 (
(
A(
x))),
Abeing a symmetric matrix and
 its spectrum.
its spectrum.
For these types of problems, we are mainly interested in
developing efficient resolution algorithms. Our basic tool is
bundling (Chap. XV of
To explore application areas where
nonsmooth optimization algorithms can be applied,
possibly after some tayloring. A rich field of such
application is combinatorial optimization, with all forms
of relaxation
To explore the possibility of
designing more sophisticated algorithms. This implies an
appropriate generalization of second derivatives when the
first derivative does not exist, and we use advanced
tools of nonsmooth analysis, for example
Application Domains
Introduction
Many systems (either actual or abstract) can be
represented by (
Mechanical systems with unilateral
constraints and dry friction (the biped robot is a
typical example), including kinematic chains with slack,
phenomena of liquid slosh, etc.
Electrical circuits with ideal diodes
and/or transistors Mos.
Optimal control with constraints on
the state, closed loop of a system controlled by an
mpcalgorithm
model predictive
control, etc.
This class of models is not too large (to allow thorough
studies), yet rich enough to include many applications. This
goes in contrast to a study of general hybrid systems. Note
for example that (
xand
uprevail in the evolution (there is no discrete control
to commute from a mode to the other: only the input
ucan be used). Let us cite some specific
applications.
Computational neuroscience
Modeling in neuroscience makes extensive use of nonlinear
dynamical systems with a huge number of interconnected
elements. Our current theoretical understanding of the
properties of neural systems is mainly based on numerical
simulations, from single cell models to neural networks. To
handle correctly the discontinuous nature of
integrate-and-fire networks, specific numerical schemes have
to be developed. Our current works focus on event-driven,
time-stepping and voltage-stepping strategies, to simulate
accurately and efficiently neuronal networks. Our activity
also includes a mathematical analysis of the dynamical
properties of neural systems. One of our aims is to
understand neural computation and to develop it as a new type
of information science.
Electronic circuits
Whether they are integrated on a single substrate or as a
set of components on a board, electronic circuits are very
often a complex assembly of many basic components with non
linear characteristics. The IC technologies now allow the
integration of hundreds of millions of transistors switching
at GHz frequencies on a die of 1cm
2. It is out of question to simulate a whole such IC
with standard tools such as the SPICE simulator. We currently
work on a dedicated plug-in able to simulate a whole circuit
comprising various components, some modelled in a nonsmooth
way.
Walking robots
As compared to rolling robots, the walking ones – for
example hexapods – possess definite advantages whenever the
ground is not plane or free: clearing obstacles is easier,
holding on the ground is lighter, adaptivity is improved.
However, if the working environment of the system is adapted
to man, the biped technology must be preferred, to preserve
good displacement abilities without modifying the
environment. This explains the interest displayed by the
international community in robotics toward humanoid systems,
whose aim is to back man in some of his activities,
professional or others. For example, a certain form of help
at home to disabled persons could be done by biped robots, as
they are able to move without any special adaptation of the
environment.
Optimization
Optimization exists in virtually all economic sectors.
Simulation tools can be used to optimize the system they
simulate. Another domain is parameter
identification(Idopt or Estime teams), where the
deviation between measurements and theoretical predictions
must be minimized. Accordingly, giving an exhaustive list of
applications is impossible. Some domains where Inria has been
implied in the past, possibly through the former Promath and
Numopt teams are: production management, geophysics, finance,
molecular modeling, robotics, networks, astrophysics,
crystallography, ...Our current applicative activity
includes: the management of electrical production
(deterministic or stochastic), the design and operation of
telecommunication networks.
Computer graphics Animation
A new application in Bipop is the simulation of complex
scenes involving many interacting objects. Whereas the
problem of collision detection has become a mature field
those recent years, simulating the collision response (in
particular frictious contacts) in a realistic, robust and
efficient way, still remains an important challenge. Another
related issue we began to study is the simulation of
heterogeneous objects such as granular or fibrous materials,
which requires the design of new high-scales models for
dynamics and contacts; indeed, for such large systems,
simulating each interacting particle/fiber individually would
be too much time-consuming for typical graphics applications.
Finally, our current activity includes the shape control of
simulated objects, which is of great importance in the field
of artistic design, for the making of movies and video games
for example. Such problems typically involve constrained
optimization.
Software
Nonsmooth dynamics: Siconos
Vincent
Acary
In the framework of the European project Siconos, Bipop
was the leader of the Work Package 2 (WP2), dedicated to the
numerical methods and the software design for nonsmooth
dynamical systems. The aim of this work is to provide a
common platform for the simulation, modeling, analysis and
control of abstract nonsmooth dynamical systems. Besides
usual quality attributes for scientific computing software,
we want to provide a common framework for various scientific
fields, to be able to rely on the existing developments
(numerical algorithms, description and modeling software), to
support exchanges and comparisons of methods, to disseminate
the know-how to other fields of research and industry, and to
take into account the diversity of users (end-users,
algorithm developers, framework builders) in building expert
interfaces in Python and end-user front-end through
Scilab.
After the requirement elicitation phase, the Siconos
Software project has been divided into 5 work packages which
are identified to software products:
Siconos/NumericsThis library contains a set of
numerical algorithms, already well identified, to solve
non smooth dynamical systems. This library is written in
low-level languages (C,F77) in order to ensure numerical
efficiency and the use of standard libraries (Blas,
Lapack, ...)
Siconos/Kernel(Engine
+Front-End)The Engine is an
object-oriented structure (C++) for modeling and
simulation of abstract dynamical systems. The Front-End
is the driver interface of the Engine thanks to two types
of API's. The first one is an API in C++, interfaced in
Python for scripting uses. The second API, in C, will be
interfaced with Scilab for a more user-friendly
platform.
Siconos/AnalysisThis part is devoted to the
stability and bifurcation analysis of nonsmooth dynamical
systems.
Siconos/ControlThis part is devoted to the
implementation of control strategies of non smooth
dynamical systems.
Siconos/imseThe final product is an Integrated modeling and
Simulation Environment dedicated to applied nonsmooth
problems.
Further informations may be found at
[http://
siconos.
gforge.
inria.
fr/
]
Humanoid motion analysis and
simulation
Pierre-Brice
Wieber
The HuMAnS toolbox offers tools for the modelling, control
and analysis of humanoid motion, be it of a robot or a human.
It is a C/C++/Scilab/Maple-based set of integrated tools for
the generation of dynamical models of articulated bodies with
unilateral contact and friction, their simulation with an
event-driven integration scheme, their 3D visualization, the
computation of stability measures, optimal positions and
trajectories, the generation of control laws and observers,
the reconstruction of movements from different sensing
systems.
Optimization
Claude
Lemaréchal
Essentially two possibilities exist to distribute our
optimization software: library programs (say Modulopt codes),
communicated either freely or not, depending on what they are
used for, and on the other hand specific software, developed
for a given application.
The following optimization codes have been developed in
the framework of the former Promath project. They are
generally available at
[http://
www-rocq.
inria.
fr/
~gilbert/
modulopt/
];
M1QN3is also
distributed under
gpl.
Code
M1QN3
Optimization without constraints for problems with many
variables (
n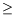 10
3, has been used for
10
3, has been used for
n= 10
6). Technically, uses a limited-memory
bfgsalgorithm
with Wolfe's line-search (see Chap. 4 of
Code
M2QN1
Optimization with simple bound-constraints for (small)
problems:
Dis a parallelotope in
R
n. Uses
bfgswith Wolfe's
line-search and active-set strategy.
Code
N1CV2
Minimization without constraints of a convex nonsmooth
function by a proximal bundle method (Chap. XV of
Modulopt
In addition to codes such as above, the Modulopt library
contains application problems, synthetic or from the real
world. It is a field for experimentation, functioning both
ways: to assess a new algorithm on a set of test-problems,
or to select among several codes one best suited to a given
problem.
Simulation of fibrous materials
Florence
Bertails-Descoubes
Gilles
Daviet
Florent
Cadoux
The goal of the MECHE ADT, started in September 2009 and
planned for 2 years, is to develop a software for simulating
the dynamics of assemblies of thin rods (such as hair),
subject to contact and friction. This software combines a
panel of well-accepted models for rods (ranging from reduced
coordinates to maximal coordinates models, and including
models recently developed by some members of the group) with
classical as well as innovative schemes for solving the
problem of frictious contact (incorporating the most recent
results of the group). The aim of this software is twofold:
first, we would like to compare and analyse the performance
of nonsmooth schemes for the frictious contact problem, in
terms of realism (capture of dry friction, typically),
robustness, and computational efficiency. This study will be
conducted onto the different rod models that are available in
the software. Second, such a software will help us understand
the behaviour of a fibrous material (such as hair) through
virtual experiments, thanks to which we hope to identify and
understand some important emergent phenomena. In the past,
such fibrous materials have been seldom studied (though many
applications have come out those years - e.g. cosmetology and
computer graphics), and we believe that numerical simulation
will give to us some important hints on how to model such a
system macroscopically.
An associate engineer, Gilles Daviet, have been hired in
September 2009 to work full-time on the MECHE project.
Contracts and Grants with Industry
Industrial contracts
ANRCheveux:
Modeling and dynamic simulation of hair in the context of
feature films production. Partners: Neomis Animation
sarl, BeeLight
sarl, Institut
Jean Le Rond d'Alembert (
upmc-cnrs), Inria
(Bipop, Evasion and Artis).
ANRSaladyn:
Numerical tools for simulating dynamics systems in mechanics;
Partners: INRIA Bipop, LMGC Montpellier, EdF, Schneider
Electric.
FUIRomeo:
Partners: Aldebaran Robotics, Acapela, As An Angel, INRIA,
Institut de la Vision, LAAS, LIMSI, LIST, LISV, LPPA,
Spirops, Telecom Paris Tech, Voxler (
[http://
www.
projetromeo.
com/
index_en.
html]).
EdF: Documentation of the
noisedfsoftware
L'OREAL: “contrat d'étude” with L'Oréal performed in
January 2010, for adding extended functionalities to the hair
simulation software transfered in 2006 (F.
Bertails-Descoubes)
Other grants
–
ANRSaladyn,
programme COSINUS.
–
ANRMultiple
Impact, programme BLANC.
–
FUIRomeo.
–
ANRCheveux.
–
ANRR-Blink,
programme Jeunes Chercheurs.
–
MSTICProjet
"math-IT" funded by Grenoble University.
–
Associate Team:
SHARE, Simulation of virtual Humans and Animals interacting
with Realistic Environments, with theuniversity of
Vancouver.
Dissemination
Software
–
M2FC1(a code for
nonsmooth-nonconvex optimization) sent to Mentor Graphics
(design of robust analog circuits).
Animation of the scientific community
B. Brogliato is:
– Member of the International Program
Committees of 7th International Multi-Conference on Systems,
Signals and Devices SSD'10, June 27-30 2010, Amman, Jordan;
7th International Conference on Informatics in Control,
Automation and Robotics ICINCO 2010, 15-18 June, Funchal,
Madeira, Portugal; Conférence Internationale Francophone
d'Automatique, CIFA 2010, 2-4 juin 2010, Nancy.
– Guest Editor (with P. Piiroinen, L.
Lopez and T. Kuepper) of the special issue “Discontinuous
Dynamical Systems: Theory and Numerical Methods” of
Mathematics and Computer in Simulation (scheduled for
2011).
F. Bertails has been a reviewer for
– ACM SIGGRAPH since 2007
– Eurographics since 2005
– ACM Solid and Physical Modeling
Symposium since 2008.
She has been a member of the national SPECIF PhD award
boarding since 2007.
– J. Malick is member of the GTAI-COST
(INRIA grant selection committee).
– J. Malick co-organized workshop on
optimization and applications (CAOA2010, January 2010) in the
occasion of the 65th birthday of Claude Lemarechal.
Teaching
– ENSIMAG: J. Malick, F.
Bertails-Descoubes: “Numerical Optimization”, 60h and 22.5h
respectively.
– Université de Limoges, laboratoire XLIM:
B. Brogliato (master 2 recherche Math. Appl., 13.5h)
– ENSIMAG: J. Malick, “Optimization
methods in finance”, ENSIMAG 3A, 20h (janv-mars 2010)
Participation to conferences, seminars
J. Malick gave a talk at:
– - ROADEF2010, Toulouse, February
2011
– - European Workshop on Mixed Integer
Nonlinear Programming, Luminy, April 2010
B. Brogliato gave a talk at
– -AIMS 8th AIMS conference Conference on
Dynamical Systems, Differential Equations and Applications,
Dresden University of Technology, Dresden, Germany, May
25-28.
– -Seminar at Université de Montpellier
(April 2010), Department of Mathematics.
– -Seminar at Université de Saint-Etienne
(December 2010), Department of Mathematics.
– -IUTAM Symposium on Nonlinear Dynamics
for Advanced Technologies and Engineering Design, university
of Aberdeen, Scotland, 27-30 July 2010.
P.B. Wieber gave talks at:
– -IROS 2010 (IEEE International
Conference on Intelligent Robots and Systems).
– -ICRA 2010 (EEE Int. Conf. on Robotics
and Automation).
– - Humanoids 2010 (IEEE International
Conference on Humanoid Robotics).
– -JNRH 2010 (Journees Nationales de
Robotique Humanoide).
![]() denotes orthogonality;
denotes orthogonality;
![]()
![]()
![]()
![]() 0is equivalent to
-
0is equivalent to
-
![]()
![]() N
N
![]() for all
for all
![]()
![]()
![]() (
(
![]() its spectrum.
its spectrum.