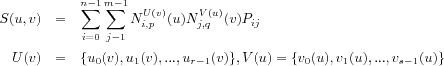Our overall objectives are to increase precision of shape modeling and processing, and more fundamentally to study mathematical and computational aspects of curves and surfaces. We thus propose to construct a new system of continuity theories, called floating-point continuities, to bridge the gap between the traditional mathematics and modern computer science. Based on the floating-point continuities and epsilon-geometry continuities approaches introduced in our recent publications, we reconsider several key geometric modeling operators.
Note that we also proposed some contributions in Computer Graphics with some Master students and with two young Tsinghua researchers, who prepared a Ph D (Weiming Dong) or a Post Doc (Bin Wang) at INRIA with us.
Continuities are the basic and important properties of shapes. Continuities of a surface can be addressed by the continuities of curves on the surface in arbitrary directions. Our prior works have found that epsilon-geometric continuities have some advantages over traditional parametric continuities and geometric continuities. Thus, we focus on designing curves with epsilon-geometric continuities and completely lying on a free form surface. This work will play an important role in surface blending, surface-surface intersection, surface trimming, numerical control (NC) tool path generation for machining surfaces, and so on as well.
To ensure positional continuity between the blending and base surfaces for example, linkage curves are usually first computed in the parametric domain, and then represented as the mapping of the domain curves on the base surfaces. To compute the exact curve on a free form surface in control point representation, many algorithms have been presented. However, the degrees of exact curves are considerably high, which results in computationally demanding evaluations and introduces numerical instability.
To overcome the problems of the exact, explicit representation, many approximation algorithms have been presented. To our knowledge, all presented approximation algorithms generate curves not lying completely on the surface.
If such a curve is used as a boundary curve of another
surface, gaps may occur between the two surfaces, which are
not acceptable in many CAD applications. In surface blending
for example, if the linkage curves are not completely on the
base surfaces, the blending surface and the base surfaces are
not even
G0continuous.
Novelty and originality:
We plan to study approximation algorithms that generate
low degree curves lying completely on the free form surfaces.
Until now, we know how to generate the initial approximate
polyline, how to control the Hausdorff distance between the
approximate curve and the user-specific tolerance and,
finally, how to generate an
![]() -
-
G1continuous curve. Our goal is to climb-up
a new step in the continuity problem. We plan to study
approximation algorithms that generate low degree curves
lying completely on the free-form surfaces and satisfying the
epsilon-continuity condition.
Up to now, almost all geometric modeling tool kits are
based on traditional mathematics. They ignore the fact that
computers can only represent a finite set of real numbers and
simply use the formula (
a-
![]() <
<
b) and (
b<
a+
![]() ) to compare whether two real
numbers
) to compare whether two real
numbers
aand
bare equal to each other or not. In the way, it becomes
a very hard problem how to choose the proper value
![]() , i.e., the precision is often out of control in
geometric modeling tool kits although few documents report
such the fact. Our previous researches showed that it would
require much more data for representing bodies as well. We
need to build new theories from traditional mathematics such
that they can well fit in with the modern computer
science.
, i.e., the precision is often out of control in
geometric modeling tool kits although few documents report
such the fact. Our previous researches showed that it would
require much more data for representing bodies as well. We
need to build new theories from traditional mathematics such
that they can well fit in with the modern computer
science.
Let's consider, for example, the problem of whether two line segments intersect in the plane in Euclidean geometry. A lot of researches on this problem focus on the accuracy of the testing results by computers. Some authors find that the errors in floating-point arithmetic may make two lines intersect more than once. Exact arithmetic methods are able to make each step of computations exact and always produce correct results. However, they require much more execution time than the inaccuracy floating-point arithmetic methods, which are frequently used. Thus, one of the research directions on this problem is to improve the efficiency of the exact arithmetic. Some authors propose a technique, named double precision geometry, which could replace exact arithmetic with rounded arithmetic in computing intersections of a set of lines or line segments. Some authors give a method to reduce the cost of exact integer arithmetic with a floating-point filter and interval analysis or provide another method, named static-analysis techniques, to reduce the cost of exact integer arithmetic.
Another research direction is to investigate how to reduce the error when using fixed length floating-point arithmetic. Following this way, we have achieved a lot of important results, such as our efficient exact floating-point summation method.
Originality and novelty:
We will propose a new approach to construct a new system of continuity theories, called floating-point continuities. Based on this theory, we propose to construct NURBS surfaces satisfying the floating-point continuity condition. With this contribution, we hope to bridge the gap between the traditional mathematics used in Shape Modeling and modern computer science and act as a pioneer in this new research avenue.
After six years, the French and Chinese partners of the
CAD Project have co-signed 85 International Publications
included 60 articles in the best Journals, Journal of
Computer Aided Design - Elsevier or in Computer Aided
Geometry Design - Elsevier, ACM Transactions on Graphics -
ACM, Graphical Models - Elsevier, Pattern Recognition -
Elsevier, 28 papers in the best international conferences and
several Technological Transfers with Chinese and European or
French Industry
Today, time has come to prepare the future. So, this year,
we spent efforts to develop new ideas, new cooperation with
French and Chinese partners and to obtain supports from
Governmental institutions as well as Industry in the two
countries. It is the reason why we want to highlight this
year the success of our young senior and juniors
partners
Prof. Xiaopeng Zhang (just promoted as a Full Professor in CASIA) for his contributions with Dr. Wujun Che in Geometry (Implicit Surfaces) published in Computer Aided Geometry Design;
Dr. Bin Wang (Tsinghua University) and Dr. Weiming Dong (CASIA) for their top level publications in Rendering (The Visual Computer, Computer Graphics Forum,) IEEE Transactions on Visualization and Computer Graphics) and Image Synthesis (The Visual Computer, ACM Transactions on Graphics);
And, last but not least, we want to underline the promising work in Geometry of our Ph. D. student, Kan-Le Shi who is going to join INRIA (Geometrica) for 4 Months;Dr. Dongming Yan, who has published at the prestigious ACM SIGGRAPH Conference in August 2010. He joined us in May and currently works at INRIA (ALICE) as a Post Doctor in Geometry.