The
plasma statecan be considered as the
fourth state of matter, obtained for example by
bringing a gas to a very high temperature (
10
4
Kor more). The thermal energy of
the molecules and atoms constituting the gas is then
sufficient to start ionization when particles collide. A
globally neutral gas of neutral and charged particles,
called
plasma, is then obtained. Intense charged particle
beams, called nonneutral plasmas by some authors, obey
similar physical laws.
The hierarchy of models describing the evolution of charged particles within a plasma or a particle beam includes:
N-body models where each particle interacts
directly with all the others,
kinetic models based on a statistical description of the particles,
fluid models valid when the particles are at a thermodynamical equilibrium.
Calvi team mainly focuses on kinetic models, but not exclusively. In particular, every kind of models are mathematically analyzed, approximate models are built and studied and model hierarchies are set out.
In a so-called
kinetic model, each particle species
sin a plasma or a particle beam is described by a
distribution function
![]() corresponding to the statistical average of the
particle distribution in phase-space corresponding to many
realisations of the physical system under investigation.
The product
corresponding to the statistical average of the
particle distribution in phase-space corresponding to many
realisations of the physical system under investigation.
The product
![]() is the average number of particles of the considered
species, the position and velocity of which are located in
a bin of volume
is the average number of particles of the considered
species, the position and velocity of which are located in
a bin of volume
![]() centered around
centered around
![]() . The distribution function contains a lot more
information than what can be obtained from a fluid
description, as it also includes information about the
velocity distribution of the particles.
. The distribution function contains a lot more
information than what can be obtained from a fluid
description, as it also includes information about the
velocity distribution of the particles.
A kinetic description is necessary in collective plasmas where the distribution function is very different from the Maxwell-Boltzmann (or Maxwellian) distribution which corresponds to the thermodynamical equilibrium, otherwise a fluid description is generally sufficient. In the limit when collective effects are dominant with respect to binary collisions, the corresponding kinetic equation is the Vlasov equation
![]()
which expresses that the distribution
function
fis conserved along the particle trajectories which
are determined by their motion in their mean
electromagnetic field. The Vlasov equation which involves a
self-consistent electromagnetic field needs to be coupled
to the Maxwell equations in order to compute this field
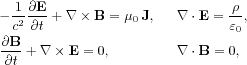
which describes the evolution of the electromagnetic field generated by the charge and current densities
![]()
associated to the charged particles.
When binary particle-particle interactions are dominant
with respect to the mean-field effects then the
distribution function
fobeys the Boltzmann equation
![]()
where
Qis the nonlinear Boltzmann collision operator. In
some intermediate cases, a collision operator needs to be
added to the Vlasov equation.
The numerical solution of the three-dimensional Vlasov-Maxwell system represents a considerable challenge due to the huge size of the problem. Indeed, the Vlasov-Maxwell system is nonlinear and posed in phase space. It thus depends on seven variables: three configuration space variables, three velocity space variables and time, for each species of particles. This feature makes it essential to use every possible option to find a reduced model wherever possible, in particular when there are geometrical symmetries or small terms which can be neglected.
Beside this, enriching and making more rigorous the model hierarchyis also an important challenge which requires a deep knowledge of different models in use in plasma physics (e.g. Magneto-Hydro-Dynamics, Laser-Matter Interaction, Waves In Plasma, etc.) and their connections with Vlasov-like models.
The mathematical analysis of the Vlasov equation is essential for a thorough understanding of the model as well for physical as for numerical purposes. It has attracted many researchers since the end of the 1970s. Among the most important results which have been obtained, we can cite the existence of strong and weak solutions of the Vlasov-Poisson system by Horst and Hunze , see also Bardos and Degond . The existence of a weak solution for the Vlasov-Maxwell system has been proved by Di Perna and Lions . An overview of the theory is presented in a book by Glassey .
Many questions concerning for example uniqueness or existence of strong solutions for the three-dimensional Vlasov-Maxwell system are still open. Moreover, their is a realm of approached models that need to be investigated. In particular, the Vlasov-Darwin model for which we could recently prove the existence of global solutions for small initial data .
On the other hand, the asymptotic study of the Vlasov equation in different physical situations is important in order to find or justify reduced models. One situation of major importance in tokamaks, used for magnetic fusion as well as in atmospheric plasmas, is the case of a large external magnetic field used for confining the particles. The magnetic field tends to incurve the particle trajectories which eventually, when the magnetic field is large, are confined along the magnetic field lines. Moreover, when an electric field is present, the particles drift in a direction perpendicular to the magnetic and to the electric field. The new time scale linked to the cyclotron frequency, which is the frequency of rotation around the magnetic field lines, comes in addition to the other time scales present in the system like the plasma frequencies of the different particle species. Thus, many different time scales as well as length scales linked in particular to the different Debye length are present in the system. Depending on the effects that need to be studied, asymptotic techniques allow to find reduced models. In this spirit, in the case of large magnetic fields, recent results have been obtained by Golse and Saint-Raymond , as well as by Brenier . Our group has also contributed to this problem using homogenization techniques to justify the guiding center model and the finite Larmor radius model which are used by physicist in this setting , , .
Another important asymptotic problem yielding reduced models for the Vlasov-Maxwell system is the fluid limit of collisionless plasmas. In some specific physical situations, the infinite system of velocity moments of the Vlasov equation can be closed after a few of those, thus yielding fluid models.
The development of efficient numerical methods is essential for the simulation of plasmas and beams. Indeed, kinetic models are posed in phase space and thus the number of dimensions is doubled. Our main effort lies in developing methods using a phase-space grid as opposed to particle methods. In order to make such methods efficient, it is essential to consider means for optimizing the number of mesh points. This is done through different adaptive strategies. In order to understand the methods, it is also important to perform their mathematical analysis. For a few years, we also have been interesting in solvers that use Particle In Cell method. This new issue allows us to enrich some parts of our research activities previously centered on the Semi-Lagrangian approach. We also have been initiating to insert asymptotic analysis products and geometry products within numerical methods in oder to enforce their robustness and their ability to perform long term simulations.
The numerical integration of the Vlasov equation is one of the key challenges of computational plasma physics. Since the early days of this discipline, an intensive work on this subject has produced many different numerical schemes. One of those, namely the Particle-In-Cell (PIC) technique, has been by far the most widely used. Indeed it belongs to the class of Monte Carlo particle methods which are independent of dimension and thus become very efficient when dimension increases which is the case of the Vlasov equation posed in phase space. However these methods converge slowly when the number of particles increases, hence if the complexity of grid based methods can be decreased, they can be the better choice in some situations. This is the reason why one of the main challenges we address is the development and analysis of adaptive grid methods.
Exploring grid based methods for the Vlasov equation, it becomes obvious that they have different stability and accuracy properties. In order to fully understand what are the important features of a given scheme and how to derive schemes with the desired properties, it is essential to perform a thorough mathematical analysis of this scheme, investigating in particular its stability and convergence towards the exact solution.
The semi-Lagrangian method consists in computing a
numerical approximation of the solution of the Vlasov
equation on a phase space grid by using the property of the
equation that the distribution function
fis conserved along characteristics. More precisely,
for any times
sand
t, we have
![]()
where
![]() are the characteristics of the Vlasov equation which
are solution of the system of ordinary differential
equations
are the characteristics of the Vlasov equation which
are solution of the system of ordinary differential
equations
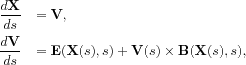
with initial conditions
![]() ,
,
![]() .
.
From this property,
fnbeing known one can induce a numerical method for
computing the distribution function
fn+ 1at the grid points
![]() consisting in the following two steps:
consisting in the following two steps:
For all
i,
j, compute the origin of the
characteristic ending at
![]() , i.e. an approximation of
, i.e. an approximation of
![]() ,
,
![]() .
.
As
![]()
fn+ 1can be computed by interpolating
fnwhich is known at the grid points at the points
![]() .
.
This method can be simplified by performing a time-splitting separating the advection phases in physical space and velocity space, as in this case the characteristics can be solved explicitly.
Uniform meshes are most of the time not efficient to solve a problem in plasma physics or beam physics as the distribution of particles is evolving a lot as well in space as in time during the simulation. In this case a variants, called adaptive semi-Lagrangian methods, of semi-Lagrangian methods was set out better to better fit the distribution of particles.
The Particle-In-Cell method consists in solving the Vlasov equation using a particle method, i.e. advancing numerically the particle trajectories which are the characteristics of the Vlasov equation, using the equations of motion which are the ordinary differential equations defining the characteristics. The self-fields are computed using a standard method on a structured or unstructured grid of physical space. The coupling between the field solve and the particle advance is done on the one hand by depositing the particle data on the grid to get the charge and current densities for Maxwell's equations and, on the other hand, by interpolating the fields at the particle positions. This coupling is one of the difficult issues and needs to be handled carefully.
The solutions to Maxwell's equations are a prioridefined in a function space such that the curl and the divergence are square integrable and that satisfy the electric and magnetic boundary conditions. Those solutions are in fact smoother (all the derivatives are square integrable) when the boundary of the domain is smooth or convex. This is no longer true when the domain exhibits non-convex geometrical singularities(corners, vertices or edges).
Physically, the electromagnetic field tends to infinity in the neighbourhood of the re-entrant singularities, which is a challenge to the usual finite element methods. Nodal elements cannot converge towards the physical solution. Edge elements demand considerable mesh refinement in order to represent those infinities, which is not only time- and memory-consuming, but potentially catastrophic when solving time dependent equations: the CFL condition then imposes a very small time step. Moreover, the fields computed by edge elements are discontinuous, which can create considerable numerical noise when the Maxwell solver is embedded in a plasma (e.g. PIC) code.
In order to overcome this dilemma, a method consists in splitting the solution as the sum of a regularpart, computed by nodal elements, and a singularpart which we relate to singular solutions of the Laplace operator, thus allowing to calculate a local analytic representation. This makes it possible to compute the solution precisely without having to refine the mesh.
This Singular Complement Method(SCM) had been developed and implemented in plane geometry.
An especially interesting case is axisymmetric geometry. This is still a 2D geometry, but more realistic than the plane case; despite its practical interest, it had been subject to much fewer theoretical studies . The non-density result for regular fields was proven , the singularities of the electromagnetic field were related to that of modified Laplacians , and expressions of the singular fields were calculated . Thus the SCM was extended to this geometry. It was then implemented by F. Assous (now at Bar-Ilan University, Israel) and S. Labrunie in a PIC–finite element Vlasov–Maxwell code .
As a byproduct, space-time regularity results were obtained for the solution to time-dependent Maxwell's equation in presence of geometrical singularities in the plane and axisymmetric cases , .
In order to set out numerical methods that can be valid even for long term simulations, two strategies may be followed. The first one is to incorporate in them asymptotic analysis concepts allowing to take into account, precisely, only the resulting mean effect of oscillations. This yields Two-Scale-Numerical-Methods which were introduced in and and which constitutes an active research activity.
The second, which also gives rise to an active research activity, consists in incorporating Hamitonian mechanics and symplectic geometry concepts while building numerical schemes.
The applications we consider lead to very large size computational problems for which we need to apply modern computing techniques enabling to use efficiently many computers including traditional high performance parallel computers and computational grids.
The full Vlasov-Maxwell system yields a very large computational problem mostly because the Vlasov equation is posed in six-dimensional phase-space. In order to tackle the most realistic possible physical problems, it is important to use all the modern computing power and techniques, in particular parallelism and grid computing.
An important issue for the practical use of the methods we develop is their parallelization. We address the problem of tuning these methods to homogeneous or heterogeneous architectures with the aim of meeting increasing computing resources requirements.
Most of the considered numerical methods apply a series of operations identically to all elements of a geometric data structure: the mesh of phase space. Therefore these methods intrinsically can be viewed as a data-parallel algorithm. A major advantage of this data-parallel approach derives from its scalability. Because operations may be applied identically to many data items in parallel, the amount of parallelism is dictated by the problem size.
Parallelism, for such data-parallel PDE solvers, is achieved by partitioning the mesh and mapping the sub-meshes onto the processors of a parallel architecture. A good partition balances the workload while minimizing the communications overhead. Many interesting heuristics have been proposed to compute near-optimal partitions of a (regular or irregular) mesh. For instance, the heuristics based on space-filing curves give very good results for a very low cost.
Adaptive methods include a mesh refinement step and can highly reduce memory usage and computation volume. As a result, they induce a load imbalance and require to dynamically distribute the adaptive mesh. A problem is then to combine distribution and resolution components of the adaptive methods with the aim of minimizing communications. Data locality expression is of major importance for solving such problems. We use our experience of data-parallelism and the underlying concepts for expressing data locality , optimizing the considered methods and specifying new data-parallel algorithms.
As a general rule, the complexity of adaptive methods requires to define software abstractions allowing to separate/integrate the various components of the considered numerical methods (see as an example of such modular software infrastructure).
Another key point is the joint use of heterogeneous architectures and adaptive meshes. It requires to develop new algorithms which include new load balancing techniques. In that case, it may be interesting to combine several parallel programming paradigms, i.e. data-parallelism with other lower-level ones.
Our general approach for designing efficient parallel algorithms is to define code transformations at any level. These transformations can be used to incrementally tune codes to a target architecture and they warrant code reusability.