Analysis of infinite-dimensional and
multidimensional systems
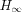 - stability of (possibly fractional) neutral delay
systems
Catherine
Bonnet
André
Fioravanti
Hitay
Özbay
Jonathan R.
Partington
- stability of (possibly fractional) neutral delay
systems
Catherine
Bonnet
André
Fioravanti
Hitay
Özbay
Jonathan R.
Partington
Both in the time-domain and frequency-domain approaches
to stability of delay systems, neutral type systems are the
most difficult systems to analyze since they may have
chains of poles asymptotic to the imaginary axis in the
complex plane. In
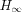 -stability are derived. Preliminary results about
the robustness relative to a change in the delay or in the
parameters are given.
-stability are derived. Preliminary results about
the robustness relative to a change in the delay or in the
parameters are given.
Numerical methods for (possibly fractional)
time-delay systems
Catherine
Bonnet
André
Fioravanti
Silviu-Iulian
Niculescu
Hitay
Özbay
Many important properties of time-delay systems cannot
be obtained in a pure algebraic form. In those cases,
numerical methods have proved to be extremely efficient and
precise. But most of the time, only classical retarded
systems are considered. We studied how those algorithms can
be adapted to the cases of neutral and fractional systems,
and if not, how to obtain new algorithms for this class of
systems
Differential flatness of analytic linear
ordinary differential systems
Alban
Quadrat
Daniel
Robertz
Based on an extension of Stafford's classical theorem in
noncommutative algebra
Serre's reduction of multidimensional
systems
Alban
Quadrat
Thomas
Cluzeau
Mohamed S.
Boudellioua
Given a linear multidimensional system (e.g.,
ordinary/partial differential systems, differential
time-delay systems, difference systems), Serre's reduction
aims at finding an equivalent linear multidimensional
system which contains fewer equations and fewer unknowns.
Finding Serre's reduction of a linear multidimensional
system can generally simplify the study of structural
properties and of different numerical analysis issues, and
it can sometimes help solving the linear multidimensional
system in closed form. In
In
The algorithms obtained in
Purity filtration of multidimensional
systems
Alban
Quadrat
In
nindependent variables is equivalent to a linear
system of partial differential defined by an upper
block-triangular matrix of partial differential operators:
each diagonal block is respectively formed by the elements
of the system satisfying an
i-dimensional (resp.,
(
n+
i)-dimensional) dynamics if the
coefficients of the system are either constant or rational
functions (resp., the coefficients are either polynomial,
formal power series or convergent power series). Hence, the
system can be integrated in cascade by successively solving
(inhomogeneous) linear
j-dimensional systems of partial differential
equations to get a Monge parametrization of its solution
space
Extendability of multidimensional linear
systems
Alban
Quadrat
Within the algebraic analysis approach to
multidimensional linear systems defined by linear systems
of partial differential equations with constant
coefficients
Symmetries and parametrizations of
multidimensional systems
Thomas
Cluzeau
Alban
Quadrat
Within the algebraic analysis approach to linear systems
theory
Factorization and decomposition problems for 2D
Stokes and Oseen equations
Thomas
Cluzeau
Alban
Quadrat
In
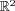 defines a cyclic differential module, we decide
about the existence of factorizations of the matrices of
differential operators defined by these systems and the
decomposition of their solution spaces in direct sums.
defines a cyclic differential module, we decide
about the existence of factorizations of the matrices of
differential operators defined by these systems and the
decomposition of their solution spaces in direct sums.
New domain decomposition methods for linear PD
systems
Thomas
Cluzeau
Victorita
Dolean
Frédéric
Nataf
Alban
Quadrat
Within the framework of the PEPS Maths-ST2I SADDLES
(Symbolic Algebra, Domain Decomposition, Linear Equations
and Systems), the purpose of this work is to use algebraic
and symbolic computation techniques such as Smith normal
forms and Gröbner basis techniques to develop new Schwarz
algorithms for domain decompositions and for
preconditionners of linear systems of partial differential
equations, especially for the Stokes and Oseen equations
studied in hydrodynamics and the Navier-Cauchy equations in
linear elasticity. New algorithms are developed to reduce
the interface conditions and to solve the completion
problem built on physical Smith variables. They are
implemented in the
Schwarzpackage
(to appear) built upon the
OreModulespackage. For more details, see
[http://
www-math.
unice.
fr/
~dolean/
saddles/
].
New techniques of observation and
control
Interval observers
Frédéric
Mazenc
Silviu-Iulian
Niculescu
Olivier
Bernard
The
interval observermethod is a recent state estimation
technique. It is used in particular in biological contexts,
where taking into account the presence of uncertainties is
essential. We have completed the theory of the linear
interval observers in several works.
1. The contribution of the work
2. The work
3. In
Finding positive solutions of systems with
delay
Frédéric
Mazenc
Silviu-Iulian
Niculescu
In
Lyapunov-based results
Frédéric
Mazenc
Claudio
De Persis
Michael
Malisoff
Marcio
De Queiroz
Olivier
Bernard
We did some works in which strict Lyapunov functions
play a central role.
1.
Systems with quantized feedback.
Quantized control systems are systems in which the
control law is a piece-wise constant function of time
taking values in a finite set. The design of quantized
control systems is based on a partition of the state space.
The aim of
2.
Strict Lyapunov functions under LaSalle
conditions.
In
3.
Adaptive control.
In
Predictive control
Sorin
Olaru
1. In
2. On NCS related topics, several results can be
mentioned with respect to the construction of polytopic
embeddings for linear systems affected by variable time
delays. In
3. The fragility of proportional-derivative controllers
has been studied in relation with robotics/tele-operation
application in the two recent publications
Comparison systems
André
Fioravanti
José
Geromel
Unicamp
Rubens
Korogui
Unicamp
A new idea to the study of
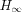 -stability and filter
-stability and filter
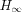 theory of LTI systems are used to derive
infinite-dimensional filters and controllers for time-delay
systems. All implementation issues are discussed in order
to provide a new and easy to implement technique.
theory of LTI systems are used to derive
infinite-dimensional filters and controllers for time-delay
systems. All implementation issues are discussed in order
to provide a new and easy to implement technique.
Discrete Markov jump systems
André
Fioravanti
José
Géromel
Unicamp
Alim
Gonçalves
Unesp
In the last years, the interest on networked control has
enormously increased. Actually, communication networks
inherently introduce packet dropouts, quantisation errors,
time-delays and limited bandwidths. Up to now, the most
successful way to model packet dropouts are stochastic
markovian systems, since they are the basic mathematical
tool for the models of many different networks. In
H2and
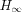 -filtering, and in
-filtering, and in
Stochastic optimization in energy production
systems
Henri
Borsenberger
Philippe
Dessante
Jorge Luis
Reyespesantez
Guillaume
Sandou
Continuing the collaboration with the Energy Department
of Supélec, the use of robust optimization methods has
allowed the computation of energy production control laws
taking into account various uncertainties on the plant.
Main uncertainties, which have been taken into account, are
the consumer load prediction, the maximum unit production
level and the production costs. Results exhibit a more
robust technical behavior together with a decrease of
global operation costs
Use of metaheuristic optimization methods for
automatic control
Gilles
Duc
Bianca Minodora
Heiman
Saïd
Ighobriouen
Gabriela
Raduinea
Guillaume
Sandou
Mohamed
Yagoubi
The development of generic methodologies for automatic
control based on metaheuristic methods has led to several
promising results. Among them are the automatic computation
of weigthing filters and the design of static
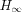 output feedbacks using Particle Swarm Optimization,
and the use of ant colony optimization for the
identification of nonlinear systems. Some promising results
have also been obtained using multiobjective Particle Swarm
Optimization
output feedbacks using Particle Swarm Optimization,
and the use of ant colony optimization for the
identification of nonlinear systems. Some promising results
have also been obtained using multiobjective Particle Swarm
Optimization
Biological systems
We solved several problems of control and stability
analysis for different types of biological models.
Control of continuous bioreactors
Frédéric
Mazenc
Jiang Zhong
Ping
Michael
Malisoff
The paper
The paper
The stabilization of equilibria in chemostats with
measurement delays is a complex and challenging problem,
and is of significant ongoing interest in bioengineering
and population dynamics. In
In
Study of a model of anaerobic digestion
process
Frédéric
Mazenc
Miled
El Hajji
Jérôme
Harmand
In
Control of a model of human heart
Frédéric
Mazenc
Michael
Malisoff
Marcio
De Queiroz
The control of human heart rate during exercise is an
important problem that has implications for the development
of protocols for athletics, assessing physical fitness,
weight management, and the prevention of heart failure. In
Modelling of hematopoiesis with application to
acute myeloid leukemia
José Luis Avila
Alonso
Houda
Benjelloun
Catherine
Bonnet
Jean
Clairambault
BANG Project-Team, INRIA
Paris-Rocquencourt
Jean-Pierre
Marie
INSERM Paris (team 18 of UMR 872), Cordeliers
Research Center ans St Antoine Hospital,
Paris
Faten
Merhi
BANG Project-Team, INRIA
Paris-Rocquencourt
Hitay
Özbay
Ruopping
Tang
INSERM Paris (team 18 of UMR 872), Cordeliers
Research Center ans St Antoine Hospital,
Paris
We have worked on a nonlinear PDE model of hematopoeisis
designed by Adimy and Crauste
A complete stability analysis with therapeutic
implications has been performed in
Through the DIGITEO project ALMA, parameters of this
model will be identified through experiments and the model
will be changed in order to take more precisely into
account some biological phenomena in hematopoiesis.
![]() -stability, BIBO-stablity, robust stability,
robustness metrics)
,
,
,
, symbolic computation
approaches (SOS methods are used for determining
easy-to-check conditions which guarantee that the poles
of a given linear system are not in the closed right
half-plane, certified CAD techniques), numerical
approaches (root-loci, continuation methods) and by means
of softwares developed in the team
,
.
-stability, BIBO-stablity, robust stability,
robustness metrics)
,
,
,
, symbolic computation
approaches (SOS methods are used for determining
easy-to-check conditions which guarantee that the poles
of a given linear system are not in the closed right
half-plane, certified CAD techniques), numerical
approaches (root-loci, continuation methods) and by means
of softwares developed in the team
,
.![]() era parametrization (which gives the set of all
stabilizing controllers of a system in terms of its
coprime factorizations) has been the cornerstone of the
success of the
era parametrization (which gives the set of all
stabilizing controllers of a system in terms of its
coprime factorizations) has been the cornerstone of the
success of the
![]() -control since this parametrization allows one to
rewrite the problem of finding the optimal stabilizing
controllers for a certain norm such as
-control since this parametrization allows one to
rewrite the problem of finding the optimal stabilizing
controllers for a certain norm such as
![]() or
or