Scientific Foundations
Modeling and landscape analysis
The modeling of problems, the analysis of structures
(landscapes) of MOPs and the performance assessment of
resolution methods are significant topics in the design of
optimization methods. The effectiveness of metaheuristics
depends on the properties of the problem and its landscape
(roughness, convexity, etc). The notion of landscape has been
first described in
Modeling of problems
Generally there are several ways of modeling a given
problem. First, one has to find the most suitable model for
the type of resolution he or she plans to use. The choice
can be made after a theoretical analysis of the model, or
after computational experiments. The choice of the model
depends on the type of method used. For example, a major
issue in the design of exact methods is to find tight
relaxations for the problem considered.
Let us note that many combinatorial optimization
problems of the literature have been studied in their
mono-objective form even if a lot of them are naturally of
a multi-objective nature.
Therefore, in the DOLPHIN project, we address the
modeling of MOPs in two phases. The first one consists in
studying the mono-objective version of the problem, where
all objectives but one are considered as constraints. In
the second phase, we propose methods to adapt the
mono-objective models or to create hand-tailored models for
the multi-objective case. The models used may come from the
first phase, or from the literature.
Analysis of the structure of a
problem
The landscape is defined by a neighborhood operator and
can be represented by a graph
G= (
V,
E). The vertices represent the
solutions of the problem and an edge
(
e
1,
e
2)exists if the solution
e2can be obtained by an application of the
neighborhood operator on the solution
e1. Then, considering this graph as the ground floor,
we elevate each solution to an altitude equals to its cost.
We obtain a surface, or landscape, made of peaks, valleys,
plateaus, cliffs, etc. The problem lies in the difficulty
to have a realistic view of this landscape.
Like others, we believe that the main point of interest
in the domain of combinatorial optimization is not the
design of the best algorithm for a large number of problems
but the search for the most adapted method to an instance
or a set of instances of a given problem. Therefore, we are
convinced that no ideal metaheuristic, designed as a
black-box, may exist.
Indeed, the first studies realized in our research group
on the analysis of landscapes of different mono-objective
combinatorial optimization problems (traveling salesman
problem, quadratic assignment problem) have shown that not
only different problems correspond to different structures
but also that different instances of the same problem
correspond to different structures.
For instance, we have realized a statistical study of
the landscapes of the quadratic assignment problem. Some
indicators that characterize the landscape of an instance
have been proposed and a taxonomy of the instances
including three classes has been deduced. Hence it is not
enough to adapt the method to the problem under study but
it is necessary to specialize it according to the type of
the treated instance.
So in its studies of mono-objective problems, the
DOLPHIN research group has introduced into the resolution
methods some information about the problem to be solved.
The landscapes of some combinatorial problems have been
studied in order to investigate the intrinsic natures of
their instances. The resulting information has been
inserted into an optimization strategy and has allowed the
design of efficient and robust hybrid methods. The
extension of these studies to multi-objective problems is a
part of the DOLPHIN project
Performance assessment
The DOLPHIN project is also interested in the
performance assessment of multi-objective optimization
methods. Nowadays, statistical techniques developed for
mono-objective problems can be adapted to the
multi-objective case. Nevertheless, specific tools are
necessary in many situations: for example, the comparison
of two different algorithms is relatively easy in the
mono-objective case - we compare the quality of the best
solution obtained in a fixed time, or the time needed to
obtain a solution of a certain quality. The same idea
cannot be immediately transposed to the case where the
output of the algorithms is a set of solutions having
several quality measures, and not a single solution.
Various indicators have been proposed in the literature
for evaluating the performance of multi-objective
optimization methods but no indicator seems to outperform
the others
Goals
One of the main issues in the DOLPHIN project is the
study of the landscape of multi-objective problems and the
performance assessment of multi-objective optimization
methods to design efficient and robust resolution
methods:
Landscape study:The goal here is to extend the
study of landscapes of the mono-objective combinatorial
optimization problems to multi-objective problems in
order to determine the structure of the Pareto frontier
and to integrate this knowledge about the problem
structure in the design of resolution methods.
This study has been initiated for the bi-objective
flow-shop problem. We have studied the convexity of the
frontiers obtained in order to show the interest of our
Pareto approach compared to an aggregation approach,
which only allows one to obtain the Pareto solutions
situated on the convex hull of the Pareto front
(supported solutions).
Our preliminary study of the landscape of the
bi-objective flow-shop problem shows that the supported
solutions are very closed to each other. This remark
leads us to improve an exact method initially proposed
for bi-objective problems. Furthermore, a new exact
method able to deal with any number of objectives has
been designed.
Performance assessment:The goal here is to
extend GUIMOO in order to provide efficient visual and
metric tools for evaluating the assessment of
multi-objective resolution methods.
Hybrid multi-objective optimization
methods
The success of metaheuristics is based on their ability to
find efficient solutions in a reasonable time
The DOLPHIN project deals with
“a posteriori”multi-objective optimization where the
set of Pareto solutions (solutions of best compromise) have
to be generated in order to give the decision maker the
opportunity to choose the solution that interests
him/her.
Population-based methods, such as
evolutionary algorithms, are well fitted for multi-objective
problems, as they work with a set of solutions
[http://
www.
lania.
mx/
~ccoello/
EMOO/
EMOObib.
html], which contains more than 5500 references. One of
the objectives of the project is to propose advanced search
mechanisms for intensification and diversification. These
mechanisms have been designed in an adaptive manner, since
their effectiveness is related to the landscape of the MOP
and to the instance solved.
In order to assess the performances of
the proposed mechanisms, we always proceed in two steps:
first, we carry out experiments on academic problems, for
which some best known results exist; second, we use real
industrial problems to cope with large and complex MOPs. The
lack of references in terms of optimal or best known Pareto
set is a major problem. Therefore, the obtained results in
this project and the test data sets will be available at the
URL
[http://
dolphin.
lille.
inria.
fr/
]at 'benchmark'.
Cooperation of metaheuristics
In order to benefit from the various advantages of the
different metaheuristics, an interesting idea is to combine
them. Indeed, the hybridization of metaheuristics allows
the cooperation of methods having complementary behaviors.
The efficiency and the robustness of such methods depend on
the balance between the exploration of the whole search
space and the exploitation of interesting areas.
Hybrid metaheuristics have received considerable
interest these last years in the field of combinatorial
optimization. A wide variety of hybrid approaches have been
proposed in the literature and give very good results on
numerous single objective optimization problems, which are
either academic (traveling salesman problem, quadratic
assignment problem, scheduling problem, etc) or real-world
problems. This efficiency is generally due to the
combinations of single-solution based methods (iterative
local search, simulated annealing, tabu search, etc) with
population-based methods (genetic algorithms, ants search,
scatter search, etc). A taxonomy of hybridization
mechanisms may be found in
LRH class - Low-level Relay Hybrid: This class
contains algorithms in which a given metaheuristic is
embedded into a single-solution metaheuristic. Few
examples from the literature belong to this class.
LTH class - Low-level Teamwork Hybrid: In this
class, a metaheuristic is embedded into a
population-based metaheuristic in order to exploit
strengths of single-solution and population-based
metaheuristics.
HRH class - High-level Relay Hybrid: Here, self
contained metaheuristics are executed in a sequence.
For instance, a population-based metaheuristic is
executed to locate interesting regions and then a local
search is performed to exploit these regions.
HTH class - High-level Teamwork Hybrid: This
scheme involves several self-contained algorithms
performing a search in parallel and cooperating. An
example will be the island model, based on GAs, where
the population is partitioned into small subpopulations
and a GA is executed per subpopulation. Some
individuals can migrate between subpopulations.
Let us notice, that if hybrid
methods have been studied in the mono-criterion case, their
application in the multi-objective context is not yet
widely spread. The objective of the DOLPHIN project is to
integrate specificities of multi-objective optimization
into the definition of hybrid models.
Cooperation between metaheuristics and exact
methods
Until now only few exact methods have been proposed to
solve multi-objective problems. They are based either on a
Branch-and-bound approach, on the algorithm
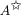 , or on dynamic programming. However, these methods
are limited to two objectives and, most of the time, cannot
be used on a complete large scale problem. Therefore, sub
search spaces have to be defined in order to use exact
methods. Hence, in the same manner as hybridization of
metaheuristics, the cooperation of metaheuristics and exact
methods is also a main issue in this project. Indeed, it
allows us to use the exploration capacity of
metaheuristics, as well as the intensification ability of
exact methods, which are able to find optimal solutions in
a restricted search space. Sub search spaces have to be
defined along the search. Such strategies can be found in
the literature, but they are only applied to mono-objective
academic problems.
, or on dynamic programming. However, these methods
are limited to two objectives and, most of the time, cannot
be used on a complete large scale problem. Therefore, sub
search spaces have to be defined in order to use exact
methods. Hence, in the same manner as hybridization of
metaheuristics, the cooperation of metaheuristics and exact
methods is also a main issue in this project. Indeed, it
allows us to use the exploration capacity of
metaheuristics, as well as the intensification ability of
exact methods, which are able to find optimal solutions in
a restricted search space. Sub search spaces have to be
defined along the search. Such strategies can be found in
the literature, but they are only applied to mono-objective
academic problems.
We have extended the previous
taxonomy for hybrid metaheuristics to the cooperation
between exact methods and metaheuristics. Using this
taxonomy, we are investigating cooperative multi-objective
methods. In this context, several types of cooperations may
be considered, according to the way the metaheuristic and
the exact method cooperate. For instance, a metaheuristic
can use an exact method for intensification or an exact
method can use a metaheuristic to reduce the search
space.
Moreover, a part of the DOLPHIN
project deals with studying exact methods in the
multi-objective context in order: i) to be able to solve
small size problems and to validate proposed heuristic
approaches; ii) to have more efficient/dedicated exact
methods that can be hybridized with metaheuristics. In this
context, the use of parallelism will push back limits of
exact methods, which will be able to explore larger size
search spaces
Goals
Based on the previous works on multi-objective
optimization, it appears that to improve metaheuristics, it
becomes essential to integrate knowledge about the problem
structure. This knowledge can be gained during the search.
This would allow us to adapt operators which may be
specific for multi-objective optimization or not. The goal
here is to design auto-adaptive methods that are able to
react to the problem structure. Moreover, regarding the
hybridization and the cooperation aspects, the objectives
of the DOLPHIN project are to deepen these studies as
follows:
Design of metaheuristics for the multi-objective
optimization:To improve metaheuristics, it becomes
essential to integrate knowledge about the problem
structure, which we may get during the execution. This
would allow us to adapt operators that may be specific
for multi-objective optimization or not. The goal here
is to design auto-adaptive methods that are able to
react to the problem structure.
Design of cooperative metaheuristics:Previous
studies show the interest of hybridization for a global
optimization and the importance of problem structure
study for the design of efficient methods. It is now
necessary to generalize hybridization of metaheuristics
and to propose adaptive hybrid models that may evolve
during the search while selecting the appropriate
metaheuristic. Multi-objective aspects have to be
introduced in order to cope with the specificities of
multi-objective optimization.
Design of cooperative schemes between exact methods
and metaheuristics:Once the study on possible
cooperation schemes is achieved, we will have to test
and compare them in the multi-objective context.
Design and conception of parallel
metaheuristics:Our previous works on parallel
metaheuristics allow us to speed up the resolution of
large scale problems. It could be also interesting to
study the robustness of the different parallel models
(in particular in the multi-objective case) and to
propose rules that determine, given a specific problem,
which kind of parallelism to use. Of course these goals
are not disjoined and it will be interesting to
simultaneously use hybrid metaheuristics and exact
methods. Moreover, those advanced mechanisms may
require the use of parallel and distributed computing
in order to easily make cooperating methods evolve
simultaneously and to speed up the resolution of large
scale problems.
Validation:In order to validate the obtained
results we always proceed in two phases: validation on
academic problems, for which some best known results
exist and use on real problems (industrial) to cope
with problem size constraints.
Moreover, those advanced mechanisms are to be used
in order to integrate the distributed multi-objective
aspects in the ParadisEO platform (see the paragraph on
software platform).
Parallel multi-objective optimization: models and
software frameworks
Parallel and distributed computing may be considered as a
tool to speedup the search to solve large MOPs and to improve
the robustness of a given method. Moreover, the joint use of
parallelism and cooperation allows improvements on the
quality of the obtained Pareto sets. Following this
objective, we will design and implement parallel models for
metaheuristics (evolutionary algorithms, tabu search
approach) and exact methods (branch-and-bound algorithm,
branch-and-cut algorithm) to solve different large MOPs.
One of the goal of the DOLPHIN project
is to integrate the developed parallel models into software
frameworks. Several frameworks for parallel distributed
metaheuristics have been proposed in the literature. Most of
them focus only either on evolutionary algorithms or on local
search methods. Only few frameworks are dedicated to the
design of both families of methods. On the other hand,
existing optimization frameworks either do not provide
parallelism at all or just supply at most one parallel model.
In this project, a new framework for parallel hybrid
metaheuristics is proposed, named
Parallel and Distributed Evolving Objects
(ParadisEO)based on EO. The framework provides in a
transparent way the hybridization mechanisms presented in the
previous section, and the parallel models described in the
next section. Concerning the developed parallel exact methods
for MOPs, we will integrate them into well-known frameworks
such as COIN.
Parallel models
According to the family of addressed metaheuristics, we
may distinguish two categories of parallel models: parallel
models that manage a single solution, and parallel models
that handle a population of solutions. The major single
solution-based parallel models are the following: the
parallel neighborhood exploration modeland the
multi-start model.
The parallel neighborhood exploration modelis
basically a "low level" model that splits the
neighborhood into partitions that are explored and
evaluated in parallel. This model is particularly
interesting when the evaluation of each solution is
costly and/or when the size of the neighborhood is
large. It has been successfully applied to the mobile
network design problem (see Application section).
The multi-start modelconsists in executing in
parallel several local searches (that may be
heterogeneous), without any information exchange. This
model raises particularly the following question: is it
equivalent to execute
klocal searches during a time
tthan executing a single local search during
k×
t? To answer this question we
tested a multi-start Tabu search on the quadratic
assignment problem. The experiments have shown that the
answer is often landscape-dependent. For example, the
multi-start model may be well-suited for landscapes
with multiple basins.
Parallel models that handle a population of solutions
are mainly: the
island model, the
central modeland
the distributed evaluation of a single solution. Let
us notice that the last model may also be used with
single-solution metaheuristics.
In
the island model, the population is split into
several sub-populations distributed among different
processors. Each processor is responsible of the
evolution of one sub-population. It executes all the
steps of the metaheuristic from the selection to the
replacement. After a given number of generations
(synchronous communication), or when a convergence
threshold is reached (asynchronous communication), the
migration process is activated. Then, exchanges of
solutions between sub-populations are realized, and
received solutions are integrated into the local
sub-population.
The central (Master/Worker) modelallows us to
keep the sequentiality of the original algorithm. The
master centralizes the population and manages the
selection and the replacement steps. It sends
sub-populations to the workers that execute the
recombination and evaluation steps. The latter returns
back newly evaluated solutions to the master. This
approach is efficient when the generation and
evaluation of new solutions is costly.
The distributed evaluation modelconsists in a
parallel evaluation of each solution. This model has to
be used when, for example, the evaluation of a solution
requires access to very large databases (data mining
applications) that may be distributed over several
processors. It may also be useful in a multi-objective
context, where several objectives have to be computed
simultaneously for a single solution.
As these models have now been identified, our objective
is to study them in the multi-objective context in order to
use them advisedly. Moreover, these models may be merged to
combine different levels of parallelism and to obtain more
efficient methods
Goals
Our objectives focus on these issues are the
following:
Design of parallel models for metaheuristics and
exact methods for MOPs: We will develop parallel
cooperative metaheuristics (evolutionary algorithms and
local search algorithms such as the Tabu search) for
solving different large MOPs. Moreover, we are
designing a new exact method, named PPM (Parallel
Partition Method), based on branch and bound and branch
and cut algorithms. Finally, some parallel cooperation
schemes between metaheuristics and exact algorithms
have to be used to solve MOPs in an efficient
manner.
Integration of the parallel models into software
frameworks: The parallel models for metaheuristics
will be integrated in the ParadisEO software framework.
The proposed multi-objective exact methods must be
first integrated into standard frameworks for exact
methods such as COIN and BOB++. A
couplingwith ParadisEO is then needed to provide
hybridization between metaheuristics and exact
methods.
Efficient deployment of the parallel models on
different parallel and distributed architecture
including GRIDs: The designed algorithms and
frameworks will be efficiently deployed on
non-dedicated networks of workstations, dedicated
cluster of workstations and SMP (Symmetric
Multi-processors) machines. For GRID computing
platforms, peer to peer (P2P) middlewares
(XtremWeb-Condor) will be used to implement our
frameworks. For this purpose, the different
optimization algorithms may be re-visited for their
efficient deployment.
Application Domains
Academic generic problems
In this project, some well known
optimization problems are re-visited in terms of
multi-objective modelization and resolution:
Workshop optimization problems:
Workshop optimization problems deal with optimizing
the production. In this project, two specific problems
are under study.
Flow-shop scheduling problem:The flow-shop
problem is one of the most well-known scheduling
problems. However, most of the works in the
literature use a mono-objective model. In general,
the minimized objective is the total completion time
(makespan). Many other criteria may be used to
schedule tasks on different machines: maximum
tardiness, total tardiness, mean job flowtime, number
of delayed jobs, maximum job flowtime, etc. In the
DOLPHIN project, a bi-criteria model, which consists
in minimizing the makespan and the total tardiness,
is studied. A tri-criteria flow-shop problem,
minimizing in addition the maximum tardiness, is also
studied. It allows us to develop and test
multi-objective (and not only bi-objective) exact
methods.
Cutting problems:Cutting problems occur when
pieces of wire, steel, wood, or paper have to be cut
from larger pieces. The objective is to minimize the
quantity of lost material. Most of these problems
derive from the classical one-dimensional
cutting-stock problem, which have been studied by
many researchers. The problem studied by the DOLPHIN
project is a two-dimensional bi-objective problem,
where rotating a rectangular piece has an impact on
the visual quality of the cutting pattern. First we
have to study the structure of the cutting-stock
problem when rotation is allowed, then we will
develop a method dedicated to the bi-objective
version of the problem.
Logistics and transportation problems:
Packing problems:In logistic and
transportation fields, packing problems may be a
major issue in the delivery process. They arise when
one wants to minimize the size of a warehouse or a
cargo, the number of boxes, or the number of vehicles
used to deliver a batch of items. These problems have
been the subjects of many papers, but only few of
them study multi-objective cases, and to our
knowledge, never from an exact point of view. Such a
case occurs for example when some pairs of items
cannot be packed in the same bin. The DOLPHIN project
is currently studying the problem in its
one-dimensional version. We plan to generalize our
approach to two and three dimensional problems, and
to more other conflict constraints, with the notion
of
distancebetween items.
Routing problems:The vehicle routing problem
(VRP) is a well-known problem and it has been studied
since the end of the 50's. It has a lot of practical
applications in many industrial areas (ex.
transportation, logistics, etc). Existing studies of
the VRP are almost all concerned with the
minimization of the total distance only. The model
studied in the DOLPHIN project introduces a second
objective, whose purpose is to balance the length of
the tours. This new criterion is expressed as the
minimization of the difference between the length of
the longest tour and the length of the shortest tour.
As far as we know, this model is one of the pioneer
work in the literature.
The second routing problem is a generalization of
the covering tour problem (CTP). In the DOLPHIN
project, this problem is solved as a bi-objective
problem where a set of constraints are modeled as an
objective. The two objectives are: i) minimization of
the length of the tour; ii) minimization of the
largest distance between a node to be covered and a
visited node. As far as we know, this study is among
the first works that tackle a classic mono-objective
routing problem by relaxing constraints and building
a more general MOP.
The third studied routing problem is the Ring Star
Problem (RSP). This problem consists in locating a
simple cycle through a subset of nodes of a graph
while optimizing two kinds of costs. The first
objective is to minimize a ring cost that is related
to the length of the cycle. The second one is to
minimize an assignment cost from non-visited nodes to
visited ones. In spite of its natural bi-criteria
formulation, this problem has always been studied in
a single-objective form where either both objectives
are combined or one objective is treated as a
constraint.
Recently, within a cooperation with SOGEP, the
logistic and delivery subsidiary company of REDCATS
(PINAULT PRINTEMPS REDOUTE), a new routing problem is
under study. Indeed, the COLIVAD project consists in
solving a logistic and transportation problem that
has been reduced to a vehicle routing problem with
additional constraints. First we are designing a
method to solve exactly a bi-objective version of the
problem in order to evaluate the interest of
modifying the current process of delivery. We are
also working on the resolution of a single-objective
version of this problem to design an operational tool
dedicated to the SOGEP problem.
For all studied problems, standard benchmarks have been
extended to the multi-objective case. The benchmarks and the
obtained results (optimal Pareto front, best known Pareto
front) are available on the Web pages associated to the
project and from the MCDM (International Society on Multiple
Criteria Decision Making) Web site. This is an important
issue to encourage comparison experiments in the research
community.
Application to mobile telecommunication
networks
With the extraordinary success of mobile telecommunication
systems, service providers have been affording huge
investments for network design and infrastructure. Mobile
network design is of outmost importance, and is thus a major
issue in mobile telecommunication systems. In fact, with the
continuous and rapid growth of communication traffic, large
scale planning becomes more and more difficult. Hence,
automatic, interactive and self-adaptive optimization
algorithms and tools would be very useful and helpful.
Advances in this area will certainly lead to important
improvements in terms of quality of service, network
management and cost deployment.
In the past, the DOLPHIN team has initiated solid
industrial collaborations within the domain of mobile
networks. In fact, the problem of network design and
frequency assignment was studied in collaboration with France
Telecom. In particular, a new formulation/resolution of the
problem as a multi-objective constrained combinatorial
optimization problem was considered. In collaboration with
Mobinets, the DOLPHIN team has also addressed the problem of
access network design. The problem consists in minimizing the
cost of the access network and maximizing its
availability.
More recently, the DOLPHIN team has been interested in new
optimization models and algorithms to address new difficult
problems raised by new emerging technologies in wireless
networks. In fact, wireless communications are evolving from
inflexible and monolithic systems to a composite radio
environment made of cognitive radio devices and networks of
different technologies. Within this context, the challenge is
to design new optimization techniques which are not only
resource, power, scale, and applications aware, but which are
self-adaptive and fully distributed in order to allow the
dynamic optimization of radio-devices behaviors depending on
the environment constraints e.g., spectrum availability,
network traffic, user demand, etc. To achieve this goal,
distributed and nature-inspired algorithms, such as
ant-colony and bees, will be investigated in order to
dynamically and distributively optimize predefined criterion
such as throughput, fairness, quality of service to cite a
few. It is expected that the techniques developed in this
work will lead to the design of new models and algorithms for
opportunistic/dynamic spectrum access and cross layer network
optimization which are at the core of future generation
wireless networks.
Application to Bioinformatics
Bioinformatic research is a great challenge for our
society and numerous research entities of different
specialities (biology, medical or information technology) are
collaborating on specific thema.
Genomic and post-genomic studies
Previous studies of the DOLPHIN project
mainly deal with genomic and postgenomic applications.
These have been realized in collaboration with academic and
industrial partners (IBL: Biology Institute of Lille; IPL:
Pasteur Institute of Lille; IT-Omics firm).
First, genomic studies aim to analyze genetic factors
which may explain multi-factorial diseases such as
diabetes, obesity or cardiovascular diseases. The
scientific goal was to formulate hypotheses describing
associations that may have any influence on diseases under
study.
Secondly, in the context of post-genomic, a very large
amount of data are obtained thanks to advanced technologies
and have to be analyzed. Hence, one of the goals of the
project was to develop analysis methods in order to
discover knowledge in data coming from biological
experiments.
These problems can be modeled as classical datamining
tasks (Association rules, feature selection). As the
combinatoric of such problems is very high and the quality
criteria not unique, we proposed to model these problems as
multi-objective combinatorial optimization problems.
Evolutionary approaches have been adopted in order to cope
with large scale problems.
Nowadays the technology is still going fast and the
number of data increases rapidly. Within the new
collaboration, started in 2010, with Genes Diffusion,
specializes in genetics and animal reproduction for bovine,
swine, equine and rabbit species, we will study
combinations of Single Nucleotide Polymorphisms (SNP) that
can explain some phenotypic characteristics.
Docking and conformational sampling
In molecular modelling, conformational sampling and
docking procedures provide help for understanding the
interaction mechanisms between (macro)molecules involved in
physiological processes. The processes to be simulated are
of a combinatorial complexity (molecule size, number of
degrees of freedom) which represents an important challenge
for the currently available computing power. Such a
challenge can be expressed by three major objectives: (1)
the proposition of mathematical models of maximum
simplicity that nevertheless provide a relevant description
of molecular behavior, (2) the development of powerful
distributed optimization algorithms (evolutionary
algorithms, local search methods, hybrid algorithms) for
sampling the molecular energy surface for stable, populated
conformations, and (3) the deployment of those intrinsic
distributed algorithms on computational Grids.
Within the framework of ANR DOCK and Decrypton projects,
the focus was to propose multi-objective formulations of
the conformational and docking problems. The goal was to
take into account different criteria characteristics of the
complex docking process. Furthermore, in order to deal with
the multimodal nature of the problems it is important to
define new hybrid mechanisms allowing us to provide
algorithms with both diversification and intensification
properties. Finally, to deal with the exponential
combinatory of these problems when large proteins are
concerned parallel and grid computing is highly required.
Using grid computing is not straightforward, so a
"gridification" process is necessary. Such process allows
us to adapt the proposed algorithms to the characteristics
of the grid. The gridification process must be exploited by
the user in a transparent way. Therefore, coupling
ParadisEO-PEO with a generic grid middleware such as Globus
is important to provide robust and efficient algorithms to
be exploited transparently.
New contacts with the Servier company show that these
questions are really challenging ones for the design of new
drug molecules.
Optimization for health care
The new collaboration (PhD thesis started in october
2010) with Alicante company, major actor in the hospital
decision making, will deal with knowledge extraction by
optimization methods for improving the process of inclusion
in clinical trials. Indeed, conducting a clinical trial,
allowing for example to measure the effectiveness of a
treatment, involves selecting a set of patients likely to
participate to this test. Currently existing selection
processes are far from optimal, and many potential patients
are not considered. The objective of this collaboration
consists in helping the practitioner to quickly determine
if a patient is interesting for a clinical trial or not.
Exploring different data sources (from a hospital
information system, patient data...), a set of decision
rules have to be generated. For this, approaches from
combinatorial optimization will be implemented, requiring
extensive work to model the problem, to define criteria
optimization and to design specific optimization
methods.
New Results
Design of the whole hierarchy of local search
algorithms on GPU
Thé Van
Luong
Nouredine
Melab
El-Ghazali
Talbi
Even if local search (LS) algorithms allow the
computational time of the solution search space exploration
to be significantly reduced, this latter cost remains
exorbitant when very large problem instances are to be
solved. Therefore, the use of GPU-based parallel computing is
required as a complementary way to speed up the search. The
main objective of our research work is to deal with such
issues for the re-design of parallel LS models to allow
solving of large scale optimization problems on GPU
architectures. Our challenge is to come out with the
GPU-based design of the whole hierarchy of parallel models.
As a main result, we already proposed methodologies for
building efficient parallel algorithms on GPUs based on the
two major models: 1) the parallel evaluation of the
neighborhood ; 2) the multi-start cooperative. Apart from
being generic, we proved the effectiveness of our proposed
methodologies by making extensive experiments. In particular,
we show that they enable to gain very significant factors in
terms of acceleration when deploying them for well-known
instances in comparison with mono-CPU architectures
GPU-based island model for evolutionary
algorithms
Thé Van
Luong
Nouredine
Melab
El-Ghazali
Talbi
In the last decades, evolutionary algorithms (EAs) have
been successfully applied to solve optimization problems.
Different models have been proposed in the literature for the
design and implementation of EAs. The island model for EAs
generally delays the global convergence of the evolution
process and encourage diversity. However, solving large-size
and time-intensive combinatorial problems with the island
model requires a large amount of computational resources. GPU
computing is recently revealed as a powerful way to harness
these resources. In
Interval-based initialization method for
permutation-based problems
Malika
Mehdi
Nouredine
Melab
El-Ghazali
Talbi
When dealing with exponential search spaces and when no
special knowledge is available on global optima, initial
populations for population-based meta-heuristics should be
uniformly distributed on the search space in order to sample
basins of attraction of all local optima. In
Parallel and distributed hybrid optimization
models for grids
Malika
Mehdi
Jean-Claude
Charr
Nouredine
Melab
El-Ghazali
Talbi
Three parallel hybridization schemes combining Genetic
Algorithms (GAs) and the Branch-and-bound (B&B) algorithm
are proposed in this work: a parallel relay model where the
two algorithms are executed in a pipeline mode, a low level
hybrid scheme where a given operator of the GA is replaced by
a B&B solver, and a cooperative hybrid scheme where the
two algorithms cooperate and exchange information about
(best-found solution, promising regions to exploit by the
B&B and unexplored regions to explore by the GA). The
particularity of these schemes is the use of a special coding
of the search space, more exactly a coded tree-based
representation already used in the B&B algorithm. Indeed,
in order to enumerate all the solutions of the search space,
the B&B algorithm progressively builds a tree that covers
the search space. Recently, a special coding for this tree
has been used to facilitate the sharing of the search between
several B&B process. Each node in the tree is assigned a
unique number and any set of contiguous nodes (successive
numbers) could be represented as an interval. The idea in
this work is to generalize this representation to
metaheuristics for a more efficient hybridization with the
B&B algorithm.
The main issue in the implementation of the hybridization
schemes previously described is that we use two different
frameworks: ParadisEO to implement the GAs and, and the BOB++
framework to develop the B&B algorithm. To facilitate any
kind of hybridization schemes between metaheuristics and the
B&B algorithm (low level, high level, relay,
cooperative), a hybridization framework integrated to
ParadisEO is developed. This framework contains template
classes that help to encapsulate any tree-based sequential
exact algorithm, in a paradisEO algorithm.
Distributed branch and bound : a new pure
peer-to-peer approach
Bilel
Derbel
Mathieu
Djamai
Nouredine
Melab
The state-of-the-art large scale approach for solving
NP-hard permutation-like problems using parallel
Branch-and-Bound (B&B) techniques is based on a
Master-Slave model which is known to be limited in terms of
scalability. In this work, we have proposed a new
Peer-to-Peer (P2P) approach that can handle a huge amount of
computational resources in a fully distributed way, that is
without the need of any centralized coordinator. In fact, we
give simple and efficient fully distributed algorithms
dealing with major parallel B&B issues, such as work
sharing, dynamic load balancing and termination detection. We
argue that our P2P approach has a scalability which is
exponentiallybetter in theory compared to the
Master-Slave technique while having a negligible
communication overhead in a worst case-scenario, namely
polylogarithmic. From the experimentation side, our
approach was implemented and deployed on top of the Grid'5000
nation-wide French grid. Through extensive simulations
involving up to 150 000 computational entities and 130
physical machines distributed over three geographical sites,
we show that, compared to the state-of-the-art Master-Slave
technique, our P2P approach enables (i) to improve the
parallel efficiency up to a ratio of 7 to 1, (ii) to
significantly speed up the B&B search process, namely by
up to 7.5 factor in terms of number of solutions explored in
the search space and, (iii) to keep the communication
overhead relatively low, namely by a factor of at most 10
without penalizing the search process.
A parallel multiple reference point approach for
multi-objective optimization
Arnaud
Liefooghe
El-Ghazali
Talbi
When approximating the efficient set, multiple reference
points can be uniformly distributed within a region that
covers the Pareto frontier. In
Metaheuristics for multi-objective bidimensional
bin packing problem
Nadia
Dahmani
François
Clautiaux
El-Ghazali
Talbi
We propose a multi-objective bidimensional bin packing
problem that consists in packing items characterized by two
sizes in two independent dimensions: a weight
ciand a volume
diinto an infinite number of identical bins with a
weight and a volume capacity C and D respectively. We stated
the mathematical formulation of the problem based on linear
programming. As a first attempt to validate the bi-objective
model, we presented different algorithms based on two
methodologies for designing and implementing multiobjective
metaheuristics namely population based and single-solution
based metaheuristics. These algorithms were implemented using
ParadisEO. Regarding the population based metaheuristics, we
design three multiobjective evolutionary algorithms. For the
single-solution based metaheuristics, we devise an iterated
tabu search algorithm and an evolutionary algorithm based on
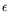 -Constraint methods. An experimental investigation is
performed on various test instances in order to illustrate
the effectiveness of the proposed algorithms in solving our
bi-objective bidimensional bin packing problem.
-Constraint methods. An experimental investigation is
performed on various test instances in order to illustrate
the effectiveness of the proposed algorithms in solving our
bi-objective bidimensional bin packing problem.
Hybrid approaches for a multi-objective bin
packing problem with conflicts
Ali
Khanafer
François
Clautiaux
El-Ghazali
Talbi
We considered a bi-objective bin packing problem with
conflicts in which we minimize the number of bins used and
the number of conflicts violated. This problem is a variation
on the bin-packing problem with conflicts, where the
resources are limited. We have modeled the problem as a
bi-objective integer linear program, and showed that the
special structure of its Pareto front allows the problem to
be reformulated as a set of mono-objective problems to be
solved iteratively. We proposed heuristics and a tabu search
to solve this mono-objective problem, and proposed a lower
bound based on column-generation and hybrid pricing
strategies. From a methodology point of view, we have
demonstrated that fast local search methods can reduce the
computational effort by a wide range. Computational
experiments show that the upper and lower bounds allow to
prove the optimality of Pareto solutions in many cases.
A network flow model for the vehicle routing
problem with time windows and multiple routes
François
Clautiaux
We addressed a variant of the Vehicle Routing Problem, the
Multi Vehicle Routing Problem with Time Windows and Multiple
Routes. It considers that a same vehicle can be assigned with
more than one route per planning period. We proposed a new
exact method for this problem. It relies on a
pseudo-polynomial network flow model whose nodes represent
the time instants, and whose arcs represent feasible vehicle
routes. We propose an iterative algorithm that uses our
model. We tested our algorithm against a set of benchmark
instances from the literature. Our method outperforms the
best method of the literature. Our method gives rise to
hybrid heuristics and meta-heuristics based on mathematical
programming.
Bi-level formulation of short-distance transport
problem and long-distance transport problem
Moustapha
Diaby
Luce
Brotcorne
El-Ghazali
Talbi
A company wants to convey different types of products from
origin i to points of destination j. It can deliver the goods
itself or hire a transport company, and subcontract part of
the application. The transport company must offer attractive
prices while aiming to maximize its profit. The aim of this
problem is to determine rates that allow the carrier to
maximize its revenues and remain affordable for the customer.
We are dealing with a bilevel problem at the first level, the
carrier (leader) wants to maximize its revenues; at the
second level, the client (follower) aims to minimize its
expenses. The transport network is defined by the graph
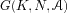 : K represents all the requests, N the nodes and
: K represents all the requests, N the nodes and
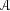 the arcs of the graph, the carrier (respectively the
company) disposes of P1(respectively P2 ) trucks
characterized by their capacity . We denote respectively by
A1 and A2 the respective arcs under the control of the
carrier and society. Those controlled by both (Carrier and
society) are represented in the graph by parallel arcs. A
price is associated with the arcs A1, and are subjected to a
constant fixed pricing unit and variable pricing unit imposed
by the carrier; arcs A2 are called free and have a fixed cost
determined by the competition. There is no loading during the
transportation. We assumed also that during a given trip the
loading phases of a truck come before unloading phases, the
two phases occur at separate times.
the arcs of the graph, the carrier (respectively the
company) disposes of P1(respectively P2 ) trucks
characterized by their capacity . We denote respectively by
A1 and A2 the respective arcs under the control of the
carrier and society. Those controlled by both (Carrier and
society) are represented in the graph by parallel arcs. A
price is associated with the arcs A1, and are subjected to a
constant fixed pricing unit and variable pricing unit imposed
by the carrier; arcs A2 are called free and have a fixed cost
determined by the competition. There is no loading during the
transportation. We assumed also that during a given trip the
loading phases of a truck come before unloading phases, the
two phases occur at separate times.
Parallel population-based metaheuristics for
solving the dynamic vehicle routing problem
Mostepha-Redouane
Khouadjia
Laetitia
Jourdan
El-Ghazali
Talbi
Many combinatorial real-world problems are mostly dynamic.
They are dynamic in the sense that the global optimum
location and its value change over the time, in contrast to
static problems. The task of the optimization algorithm is to
track this shifting optimum. Particle Swarm Optimization
(PSO) has been previously used to solve continuous dynamic
optimization problems, whereas only a few works have been
proposed for combinatorial ones. One of the most interesting
dynamic problems is the Dynamic Vehicle Routing Problem
(DVRP). In
Fitness landscapes: local optima
network
Sébastien
Verel
In
Landscape analysis for multi-objective
combinatorial optimization
Sébastien
Verel
Arnaud
Liefooghe
Laetitia
Jourdan
Clarisse
Dhaenens
Recently, the property of connectedness has been claimed
to give a strong motivation on the design of local search
techniques for multiobjective combinatorial optimization.
Indeed, when connectedness holds, a basic Pareto local
search, initialized with at least one non-dominated solution,
allows the efficient set to be identified exhaustively.
However, this becomes quickly infeasible in practice as the
number of efficient solutions typically grows exponentially
with the instance size. We propose biobjective multiple and
long path problems to show experimentally that, on the first
problem, even if the efficient set is connected, a local
search may be outperformed by a simple evolutionary algorithm
in the sampling of the efficient set. At the opposite, on the
second problem, a local search algorithm may successfully
approximate a disconnected efficient set. Then, we argue that
connectedness is not the single property to study for the
design of multiobjective metaheuristics.
One of the most commonly-used metaphors to describe the
process of heuristic search methods in solving combinatorial
optimization problems is Fitness Landscape (FiL). However, no
definition of FiL establishes an equivalence in the context
of multiobjective optimization, where two mains approaches
are generally defined: scalar and Pareto-based methods. The
efficiency of such strategies depends on the problem
properties in general, and in the correlation degree between
objective functions in particular. We here define a
systematic method to construct multiobjective problems with
correlated objective functions, and we extend the well-known
multiobjective NK-landscapes. By measuring features on the
search space (size of the efficient set, number of supported
solutions, connectedness), we show the importance of
objective correlation on the design of efficient heuristic
approaches. In terms of local optimality, we examine a
possible definition where the points represent feasible
solutions in the decision space and the "height" represents
their vector fitness function. In such a case, the standard
definition of local optimum turns into the definition of
Pareto local optimum, and the definition of global optimum to
the Pareto optimal set. In this context, it is still possible
to define the ruggedness of a given landscape. The analysis
of such concepts for a given problem is relevant to obtain
deep information about its optimization difficulty.
Unfortunately, these approaches fail to explain the dynamics
of some local search heuristics. In
Landscape analysis for logistic
problems
Marie-Éléonore
Marmion
Laetitia
Jourdan
Clarisse
Dhaenens
A state-of-the-art on existing statistical indicators of
the literature for analyzing the landscape of an optimization
problem has been performed. We classify the indicators into
three categories according to whether they characterize the
search space or the fitness space or the landscape entirely.
Thus, we can measure the impact of the neighborhood relation
and the fitness function independently or not. These
indicators have been applied to two logistic problems : a
scheduling problem (FSP)
![]() , or on dynamic programming. However, these methods
are limited to two objectives and, most of the time, cannot
be used on a complete large scale problem. Therefore, sub
search spaces have to be defined in order to use exact
methods. Hence, in the same manner as hybridization of
metaheuristics, the cooperation of metaheuristics and exact
methods is also a main issue in this project. Indeed, it
allows us to use the exploration capacity of
metaheuristics, as well as the intensification ability of
exact methods, which are able to find optimal solutions in
a restricted search space. Sub search spaces have to be
defined along the search. Such strategies can be found in
the literature, but they are only applied to mono-objective
academic problems.
, or on dynamic programming. However, these methods
are limited to two objectives and, most of the time, cannot
be used on a complete large scale problem. Therefore, sub
search spaces have to be defined in order to use exact
methods. Hence, in the same manner as hybridization of
metaheuristics, the cooperation of metaheuristics and exact
methods is also a main issue in this project. Indeed, it
allows us to use the exploration capacity of
metaheuristics, as well as the intensification ability of
exact methods, which are able to find optimal solutions in
a restricted search space. Sub search spaces have to be
defined along the search. Such strategies can be found in
the literature, but they are only applied to mono-objective
academic problems.