Scientific Foundations
Introduction
In this section, the main features for the key monitoring
issues, namely identification, detection, and diagnostics,
are provided, and a particular instantiation relevant for
vibration monitoring is described.
It should be stressed that the foundations for
identification, detection, and diagnostics, are fairly
general, if not generic. Handling high order linear dynamical
systems, in connection with finite elements models, which
call for using subspace-based methods, is specific to
vibration-based SHM. Actually, one particular feature of
model-based sensor information data processing as exercised
in I4S, is the combined use of black-box or semi-physical
models together with physical ones. Black-box and
semi-physical models are, for example, eigenstructure
parameterizations of linear MIMO systems, of interest for
modal analysis and vibration-based SHM. Such models are
intended to be identifiable. However, due to the large model
orders that need to be considered, the issue of model order
selection is really a challenge. Traditional advanced
techniques from statistics such as the various forms of
Akaike criteria (AIC, BIC, MDL, ...) do not work at all. This
gives rise to new research activities specific to handling
high order models.
Our approach to monitoring assumes that a model of the
monitored system is available. This is a reasonable
assumption, especially within the SHM areas. The main feature
of our monitoring method is its intrinsic ability to the
early warning of small deviations of a system with respect to
a reference (safe) behavior under usual operating conditions,
namely without any artificial excitation or other external
action. Such a normal behavior is summarized in a reference
parameter vector
 0, for example a collection of modes and
mode-shapes.
0, for example a collection of modes and
mode-shapes.
Identification
The behavior of the monitored continuous system is assumed
to be described by a parametric model
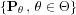 , where the distribution of the observations (
, where the distribution of the observations (
Z0, ...,
ZN) is characterized by the parameter vector

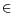
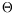 . An
estimating function, for example of the
form :
. An
estimating function, for example of the
form :
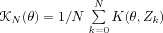
is such that
![Im3 ${\#119812 _\#952 {[\#119974 _N{(\#952 )}]}=0}$](math_image_3.png) for all
for all

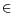
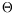 . In many situations,
. In many situations,
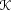 is the gradient of a function to be minimized :
squared prediction error, log-likelihood (up to a sign), ....
For performing model identification on the basis of
observations
(
is the gradient of a function to be minimized :
squared prediction error, log-likelihood (up to a sign), ....
For performing model identification on the basis of
observations
(
Z
0, ...,
Z
N), an estimate of the unknown parameter is then
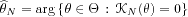
Assuming that
 *is the true parameter value, and that
*is the true parameter value, and that
![Im6 ${\#119812 _\#952 ^*{[\#119974 _N{(\#952 )}]}=0}$](math_image_6.png) if and only if
if and only if
 =
=
 *with
*with
 *fixed (identifiability condition), then
*fixed (identifiability condition), then
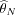 converges towards
converges towards
 *. Thanks to the central limit theorem, the vector
*. Thanks to the central limit theorem, the vector
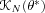 is asymptotically Gaussian with zero mean, with
covariance matrix
is asymptotically Gaussian with zero mean, with
covariance matrix
 which can be either computed or estimated. If,
additionally, the matrix
which can be either computed or estimated. If,
additionally, the matrix
![Im9 ${\#119973 _N=-\#119812 _\#952 ^*{[{\#119974 }_N^'{(\#952 ^*)}]}}$](math_image_9.png) is invertible, then using a Taylor expansion and the
constraint
is invertible, then using a Taylor expansion and the
constraint
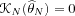 , the asymptotic normality of the estimate is
obtained :
, the asymptotic normality of the estimate is
obtained :
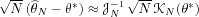
In many applications, such an approach must be improved in
the following directions :
Recursive estimation:the ability to compute
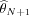 simply from
simply from
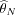 ;
;
Adaptive estimation:the ability to
trackthe true parameter
 *when it is time-varying.
*when it is time-varying.
Detection
Our approach to on-board detection is based on the
so-called asymptotic statistical local approach, which we
have extended and adapted
For achieving the early detection of small deviations with
respect to the normal behavior, our approach generates, on
the basis of the reference parameter vector
 0and a new data record, indicators which automatically
perform :
0and a new data record, indicators which automatically
perform :
The early detection of a slight
mismatch between the model and the data;
A preliminary diagnostics and
localization of the deviation(s);
The tradeoff between the magnitude of
the detected changes and the uncertainty resulting from
the estimation error in the reference model and the
measurement noise level.
These indicators are computationally cheap, and thus can
be embedded. This is of particular interest in some
applications, such as flutter monitoring, as explained in
module
As in most fault detection approaches, the key issue is to
design a
residual, which is ideally close to zero under normal
operation, and has low sensitivity to noises and other
nuisance perturbations, but high sensitivity to small
deviations, before they develop into events to be avoided
(damages, faults, ...). The originality of our approach is
to :
Designthe residual basically as a
parameter estimating function,
Evaluatethe residual thanks to a kind of central
limit theorem, stating that the residual is
asymptotically Gaussian and reflects the presence of a
deviation in the parameter vector through a change in its
own mean vector, which switches from zero in the
reference situation to a non-zero value.
This is actually a strong result, which transforms any
detection problem concerning a parameterized stochastic
processinto the problem of monitoring the mean of a
Gaussian
vector.
The behavior of the monitored system is again assumed to
be described by a parametric model
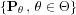 , and the safe behavior of the process is assumed to
correspond to the parameter value
, and the safe behavior of the process is assumed to
correspond to the parameter value
 0. This parameter often results from a preliminary
identification based on reference data, as in module
0. This parameter often results from a preliminary
identification based on reference data, as in module
Given a new
N-size sample of sensors data, the following question
is addressed :
Does the new sample still correspond to the nominal model
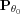 ?One manner to address this generally
difficult question is the following. The asymptotic local
approach consists in deciding between the nominal hypothesis
and a
closealternative hypothesis, namely :
?One manner to address this generally
difficult question is the following. The asymptotic local
approach consists in deciding between the nominal hypothesis
and a
closealternative hypothesis, namely :
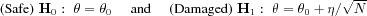
where
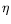 is an unknown but fixed change vector. A residual is
generated under the form :
is an unknown but fixed change vector. A residual is
generated under the form :
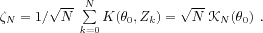
If the matrix
![Im16 ${\#119973 _N=-~\#119812 _\#952 _0{[{\#119974 }_N^'{(\#952 _0)}]}}$](math_image_16.png) converges towards a limit
converges towards a limit
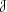 , then the central limit theorem shows
, then the central limit theorem shows
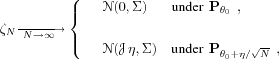
where the asymptotic covariance
matrix
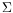 can be estimated, and manifests the deviation in the
parameter vector by a change in its own mean value. Then,
deciding between
can be estimated, and manifests the deviation in the
parameter vector by a change in its own mean value. Then,
deciding between
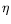 = 0and
= 0and
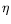
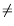 0amounts to compute the following
0amounts to compute the following
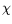 2-test, provided that
2-test, provided that
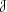 is full rank and
is full rank and
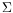 is invertible :
is invertible :
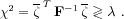
where
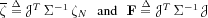
With this approach, it is possible to decide, with a
quantifiable error level, if a residual value is
significantly different from zero, for assessing whether a
fault/damage has occurred. It should be stressed that the
residual and the sensitivity and covariance matrices
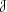 and
and
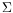 can be evaluated (or estimated) for the nominal model.
In particular, it is
notnecessary to re-identify the model, and the
sensitivity and covariance matrices can be pre-computed
off-line.
can be evaluated (or estimated) for the nominal model.
In particular, it is
notnecessary to re-identify the model, and the
sensitivity and covariance matrices can be pre-computed
off-line.
Diagnostics
A further monitoring step, often called
fault isolation, consists in determining which
(subsets of) components of the parameter vector
 have been affected by the change. Solutions for that
are now described. How this relates to diagnostics is
addressed afterwards.
have been affected by the change. Solutions for that
are now described. How this relates to diagnostics is
addressed afterwards.
Isolation.
The question:
which (subsets of) components of
 have changed ?, can be addressed using either
nuisance parameters elimination methods or a multiple
hypotheses testing approach
have changed ?, can be addressed using either
nuisance parameters elimination methods or a multiple
hypotheses testing approach
The fault vector
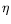 is partitioned into an informative part and a
nuisance part, and the sensitivity matrix
is partitioned into an informative part and a
nuisance part, and the sensitivity matrix
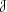 , the Fisher information matrix
, the Fisher information matrix
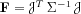 and the normalized residual
and the normalized residual
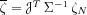 are partitioned accordingly
are partitioned accordingly
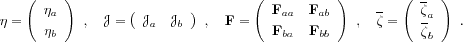
A rather intuitive statistical solution
to the isolation problem, which can be called
sensitivityapproach, consists in projecting the
deviations in
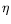 onto the subspace generated by the components
onto the subspace generated by the components
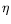
ato be isolated, and deciding between
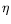
a=
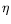
b= 0and
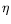
a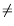 0,
0,
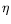
b= 0. This results in the following test
statistics :
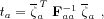
where
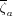 is the partial residual (score). If
is the partial residual (score). If
ta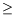
tb, the component responsible for the fault is
considered to be
arather than
b.
Another statistical solution to the problem of
isolating
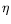
aconsists in viewing parameter
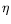
bas a nuisance, and using an existing method for
inferring part of the parameters while ignoring and being
robust to the complementary part. This method is called
min-max approach. It consists in replacing the
nuisance parameter component
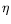
bby its least favorable value, for deciding between
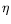
a= 0and
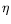
a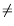 0, with
0, with
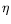
bunknown. This results in the following test
statistics :
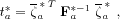
where
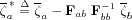 is the effective residual (score) resulting from the
regression of the informative partial score
is the effective residual (score) resulting from the
regression of the informative partial score
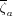 over the nuisance partial score
over the nuisance partial score
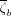 , and where the Schur complement
, and where the Schur complement
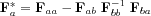 is the associated Fisher information matrix. If
is the associated Fisher information matrix. If
ta*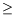
tb*, the component responsible for the fault is
considered to be
arather than
b.
The properties and relationships of these two types of
tests are investigated in
Diagnostics.
In most SHM applications, a complex physical system,
characterized by a generally non identifiable parameter
vector
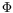 has to be monitored using a simple (black-box) model
characterized by an identifiable parameter vector
has to be monitored using a simple (black-box) model
characterized by an identifiable parameter vector
 . A typical example is the vibration monitoring
problem in module
. A typical example is the vibration monitoring
problem in module
 and diagnosis in terms of the parameter vector
and diagnosis in terms of the parameter vector
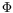 of the underlying physical model.
of the underlying physical model.
The isolation methods sketched above are possible
solutions to the former. Our approach to the latter
diagnosis problem is basically a detection approach again,
and not a (generally ill-posed) inverse problem estimation
approach
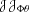 , where
, where
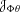 is the Jacobian matrix at
is the Jacobian matrix at
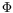 0of the application
0of the application
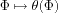 , and to use the sensitivity test (
, and to use the sensitivity test (
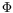 . Typically this results in the following type of
directional test :
. Typically this results in the following type of
directional test :
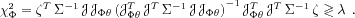
It should be clear that the selection of
a particular parameterization
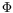 for the physical model may have a non negligible
influence on such type of tests, according to the numerical
conditioning of the Jacobian matrices
for the physical model may have a non negligible
influence on such type of tests, according to the numerical
conditioning of the Jacobian matrices
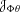 .
.
As a summary, the machinery in modules
The key issue to be addressed within each parametric
model class is the residual generation, or equivalently the
choice of the
parameter estimating function.
Subspace-based identification and
detection
For reasons closely related to the vibrations monitoring
applications described in module
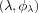 of the state transition matrix
of the state transition matrix
Fof a linear dynamical state-space system :
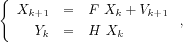
namely the
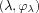 defined by :
defined by :
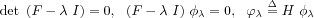
The (canonical) parameter vector in that
case is :
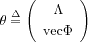
where
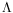 is the vector whose elements are the eigenvalues
is the vector whose elements are the eigenvalues
 ,
,
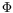 is the matrix whose columns are the
is the matrix whose columns are the
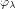 's, and
vecis the column stacking
operator.
's, and
vecis the column stacking
operator.
Subspace-based methods is the generic name for linear
systems identification algorithms based on either time domain
measurements or output covariance matrices, in which
different subspaces of Gaussian random vectors play a key
role
Covariance-driven subspace
identification.
Let
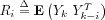 and:
and:
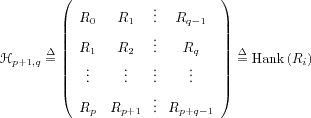
be the output covariance and Hankel
matrices, respectively; and:
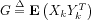 . Direct computations of the
. Direct computations of the
Ri's from the equations (
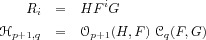
where:
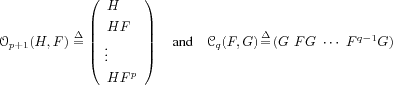
are the observability and
controllability matrices, respectively. The observation
matrix
His then found in the first block-row of the
observability matrix
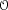 . The state-transition matrix
. The state-transition matrix
Fis obtained from the shift invariance property
of
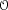 . The eigenstructure
. The eigenstructure
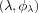 then results from (
then results from (
Since the actual model order is generally not known,
this procedure is run with increasing model orders.
Model parameter characterization.
Choosing the eigenvectors of matrix
Fas a basis for the state space of model (
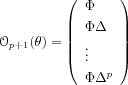
where
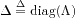 , and
, and
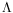 and
and
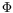 are as in (
are as in (
 0fits a given output covariance sequence
(
0fits a given output covariance sequence
(
R
j)
jis characterized by
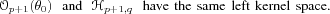
This property can be checked as follows.
From the nominal
 0, compute
0, compute
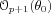 using (
using (
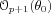 for extracting a matrix
for extracting a matrix
Usuch that:
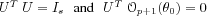
Matrix
Uis not unique (two such matrices relate through a
post-multiplication with an orthonormal matrix), but can be
regarded as a function of
 0. Then the characterization writes:
0. Then the characterization writes:
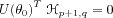
Residual associated with subspace
identification.
Assume now that
a reference
 0and a new sample
0and a new sample
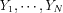 are available.For checking whether the data
agree with
are available.For checking whether the data
agree with
 0, the idea is to compute the empirical Hankel
matrix
0, the idea is to compute the empirical Hankel
matrix
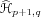 :
:
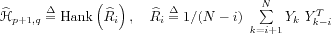
and to define the residual vector:
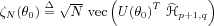
Let
 be the actual parameter value for the system which
generated the new data sample, and
be the actual parameter value for the system which
generated the new data sample, and
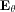 be the expectation when the actual system parameter
is
be the expectation when the actual system parameter
is
 . From (
. From (
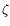
N(
 0)has zero mean when no change occurs in
0)has zero mean when no change occurs in
 , and nonzero mean if a change occurs. Thus
, and nonzero mean if a change occurs. Thus
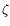
N(
 0)plays the role of a residual.
0)plays the role of a residual.
It is our experience that this residual has highly
interesting properties, both for damage detection
Other uses of the key
factorizations.
Factorization (
 in (
in (
Proving consistency and robustness
results
Designing an extension of
covariance-driven subspace identification algorithm
adapted to the presence and fusion of
non-simultaneously recorded multiple sensors setups
Proving the consistency and
robustness of this extension
Designing various forms of
input-outputcovariance-driven subspace
identification algorithms adapted to the presence of
both known inputs and unknown excitations
Application Domains
Introduction
In this section, the problems we are faced with
vibration-based monitoring and within our two major
application domains are briefly described.
Vibrations-based monitoring
Detecting and localizing damages for monitoring the
integrity of structural and mechanical systems is a topic of
growing interest, due to the aging of many engineering
constructions and machines and to increased safety norms.
Many current approaches still rely on visual inspections or
localnon destructive evaluations performed manually.
This includes acoustic, ultrasonic, radiographic or
eddy-current methods; magnet or thermal field techniques,
.... These experimental approaches
assume an
a prioriknowledge and the accessibility of a
neighborhood of the damage location. Automatic
globalvibration-based monitoring techniques have been
recognized to be useful alternatives to those local
evaluations
A common feature of the structures to be monitored (e.g.
civil engineering structures subject to hurricanes or
earthquakes, but also swell, wind and rain; aircrafts subject
to strength and turbulences,
...) is the following. These
systems are subject to both fast and unmeasured variations in
their environment and small slow variations in their
vibrating characteristics. The available data (measurements
from e.g. strain gauges or accelerometers) do not separate
the effects of the external forces from the effect of the
structure. The external forces vary more rapidly than the
structure itself (fortunately !), damages or fatigues on
the structure are of interest, while any change in the
excitation is meaningless. Expert systems based on a
human-like exploitation of recorded spectra can hardly work
in such a case : the changes of interest (1% in
eigenfrequencies) are visible neither on the signals nor on
their spectra. A global health monitoring method must rather
rely on a model that will help in discriminating between the
two mixed causes of the changes that are contained in the
measurements.
Classical modal analysis and vibration monitoring methods
basically process data registered either on test beds or
under specific excitation or rotation speed conditions.
However there is a need for vibration monitoring algorithms
devoted to the processing of data recorded in-operation,
namely during the actual functioning of the considered
structure or machine, without artificial excitation, speeding
down or stopping.
Health monitoring techniques based on processing vibration
measurements basically handle two types of characteristics:
the
structural parameters(mass, stiffness, flexibility,
damping) and the
modal parameters(modal frequencies, and associated
damping values and mode-shapes); see
Controlling the computational complexity of the processing
of the collected data is another standard monitoring
requirement, which includes a limited use of an analytical
model of the structure. Moreover, the reduction from the
analytical model to the experimental model (truncated modal
space) is known to play a key role in the success of
model-based damage detection and localization.
The approach which we have been developing, based on the
foundations in modules
Civil engineering
Civil engineering is a currently renewing scientific
research area, which can no longer be restricted to the
single mechanical domain, with numerical codes as its central
focus. Recent and significant advances in physics and
physical chemistry have improved the understanding of the
detailed mechanisms of the constitution and the behavior of
various materials (see e.g. the multi-disciplinary general
agreement
cnrs-Lafarge).
Moreover, because of major economical and societal issues,
such as durability and safety of infrastructures, buildings
and networks, civil engineering is evolving towards a
multi-disciplinary field, involving in particular information
sciences and technologies and environmental sciences.
These last ten years, monitoring the integrity of the
civil infrastructure has been an active research topic,
including in connected areas such as automatic control, for
mastering either the aging of the bridges, as in America (US,
Canada) and Great Britain, or the resistance to seismic
events and the protection of the cultural heritage, as in
Italy and Greece. The research effort in France seems to be
more recent, maybe because a tendency of long term design
without fatigue oriented inspections, as opposite to less
severe design with planned mid-term inspections. One of the
current thematic priorities of the Réseau de Génie Civil et
Urbain (RGCU) is devoted to constructions monitoring and
diagnostics. The picture in Asia (Japan, and also China) is
somewhat different, in that the demand for automatic data
processing for global SHM systems is much higher, because
recent or currently built bridges are equipped with hundreds
if not thousands of sensors, in particular the Hong
Kong-Shenzen Western Corridor and Stonecutter Bridge
projects.
Among the challenges for vibration-based bridges health
monitoring, two major issues are the different kinds of (non
measured) excitation sources and the environmental effects
Aeronautics
The aging of aerospace structures is a major current
concern of civilian and military aircraft operators. Another
key driving factor for SHM is to increase the operation and
support efficiency of an air vehicle fleet. A SHM system is
viewed as a component of a global integrated vehicle health
management (IVHM) system. An overview of the users needs can
be found in
Improved safety and performance and reduced aircraft
development and operating costs are other major concerns. One
of the critical design objectives is to clear the aircraft
from unstable aero-elastic vibrations (flutter) in all flight
conditions. This requires a careful exploration of the
dynamical behavior of the structure subject to vibration and
aero-servo-elastic forces. This is achieved via a combination
of ground vibration tests and in-flight tests. For both types
of tests, various sensors data are recorded, and modal
analyses are performed. Important challenges of the in-flight
modal analyses are the limited choices for measured
excitation inputs, and the presence of unmeasured natural
excitation inputs (turbulence). A better exploitation of
flight test data can be achieved by using output-only system
identification methods, which exploits data recorded under
natural excitation conditions (e.g., turbulent), without
resorting to artificial control surface excitation and other
types of excitation inputs
A crucial issue is to ensure that the newly designed
airplane is stable throughout its operating range. A critical
instability phenomenon, known under the name of
“aero-elastic flutter, involves the unfavorable
interaction of aerodynamic, elastic, and inertia forces on
structures to produce an unstable oscillation that often
results in structural failure”
Until the late nineties, most approaches to flutter
clearance have led to
data-basedmethods, processing different types of data.
A
combined data-based and model-basedmethod has been
introduced recently under the name of flutterometer. Based on
an aero-elastic state-space model and on frequency-domain
transfer functions extracted from sensor data under
controlled excitation, the flutterometer computes on-line a
robust flutter margin using the
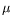 -method for analyzing the worst case effects of model
uncertainty. In recent comparative evaluations using
simulated and real data
-method for analyzing the worst case effects of model
uncertainty. In recent comparative evaluations using
simulated and real data
Algorithms achieving the
on-line in-flightexploitation of flight test data are
expected to allow a more direct exploration of the flight
domain, with improved confidence and reduced costs. Among
other challenges, one important issue to be addressed on-line
is the flight flutter monitoring problem, stated as the
problem of monitoring some specific damping coefficients. On
the other hand, it is known, e.g. from Cramer-Rao bounds,
that damping factors are difficult to estimate accurately.
For improving the estimation of damping factors, and moreover
for achieving this in real-time during flight tests, one
possible although unexpected route is to rely on detection
algorithms able to decide whether some damping factor
decreases below some critical value or not. The rationale is
that detection algorithms usually have a much shorter
response time than identification algorithms.
Software
COSMAD : Modal analysis and health monitoring
Scilab toolbox
Laurent
Mevel
corresponding person
Maurice
Goursat
With the help of Yann Veillard, Auguste Sam and Simon
Berger, former engineers, Laurent Mevel and Maurice Goursat
have developed a Scilab toolbox devoted to modal analysis and
vibration monitoring of structures or machines subjected to
known or ambient (unknown) excitation
This software (COSMAD 3.64) has been registered at the APP
under the number
IDDN.FR.001.210011.002.S.A.2003.000.20700
and can be down-loaded from
[http://
www.
irisa.
fr/
i4s/
cosmad/
]. A list of test-cases (simulators,
laboratory test-beds, real structures) for which COSMAD has
been used is available from
[http://
www.
irisa.
fr/
i4s/
cases.
pdf].
COSMAD performs the following tasks :
Output-only (O/O) subspace-based identification,
The problem is to identify the eigenstructure
(eigenvalues and observed components of the associated
eigenvectors) of the state transition matrix of a linear
dynamical system, using only the observation of some
measured outputs summarized into a sequence of covariance
matrices corresponding to successive time shifts. An
overview of this method can be found in
Input-output (I/O) subspace-based identification,
The problem is again to identify the eigenstructure, but
now using the observation of some measured inputs and
outputs summarized into a sequence of cross-covariance
matrices. This method is described in
Automatic subspace-based modal analysis, a
pre-tuned version of the O/O and I/O identification
methods above. This is described in
Automated on-line identification package, The main
question is to react to non stationarities and
fluctuations in the evolution of the modes, especially
the damping. The developed package allows the extraction
of such modes using a graphical interface allowing us to
follow the evolution of all frequencies and damping over
time and to analyze their stabilization diagram (from
which they were extracted). Automated modal extraction is
performed based on the automated analysis and
classification of the stabilization diagram. For this
method, see
Automatic recursive subspace-based modal analysis,
a sample point-wise version of the O/O and I/O
identification algorithms above. For this method,
see
Subspace-based identification through moving sensors
data fusion, The problem is to identify the
eigenstructure based on a joint processing of signals
recorded at different time periods, under different
excitations, and with different sensors pools. The key
principles are described in
Damage detection, working batch-wise,
Based on vibrations measurements processing, the
problem is to perform early detection of small deviations
of the structure w.r.t. a reference behavior considered
as normal. Such an early detection of small deviations is
mandatory for fatigue prevention. The algorithm confronts
a new data record, summarized by covariance matrices, to
a reference modal signature. The method is described
in
Damage monitoring, a sample point-wise version of
the damage detection algorithm above. This is described
in
On-line flutter onset detection, This algorithm
detects that one damping coefficient crosses a critical
value from above. For this method see
Modal diagnosis, working batch-wise, This
algorithm finds the modes the most affected by the
detected deviation. For this method, see
Damage localization,
The problem is to find the part of the structure, and
the associated structural parameters (e.g. masses,
stiffness coefficients) that have been affected by the
damage. We state and solve this problem as a detection
problem, and not an (ill-posed) inverse estimation
problem. This is explained in
Optimal sensor positioning for monitoring. At the
design stage of the monitoring system, a criterion is
computed, which quantifies the relevance of a given
sensor number and positioning for the purpose of
structural health monitoring. For this criterion, see the
articles
The modules have been tested by different partners,
especially the French industrial partners, EADS, Dassault and
Sopemea, within the FliTE2 project, by partners from the past
CONSTRUCTIF project
This Scilab toolbox continues to play the role of a
programming and development environment for all our newly
designed algorithms. Moreover, offering a
maintainedScilab platform turns out to be a crucial
factor in convincing industrial partners to undergo joint
investigations with us or to involve us within partnerships
in FP7 integrated projects proposals.
Contracts and Grants with Industry
FP7-NMP CP-IP 213968-2 IRIS
Michael
Döhler
Laurent
Mevel
Xuan
Lam
Contract INRIA 3947
I4S is involved in the core consortium of FP7-NMP Large
Scale Integrated Project.
IRIS (
Integrated European Industrial Risk Reduction System),
which helds its kick off meeting in October 2008. This
project has been elaborated within the framework of the SAMCO
association. I4S is involved in the online monitoring
sub-project.
The FP7 IRIS project about Risk assessment involves 40
partners and is headed by Helmut Wenzel, VCE (Austria), a SME
company. INRIA is involved in Group 3 about Structural Health
Monitoring. I4S works with Sheffield University and BAM
(Germany) for development of tools for structural damage
detection for bridges and wind farms. Laurent Mevel is also
member of the core IRIS Vision group, and is responsible of
the scientific coherency of the project.
SIMS
Laurent
Mevel
Michael
Döhler
I4S has signed a collaborative agreement with SVIBS. This
leads to SVIBS bringing INRIA into a 12 year long SHM project
in Canada with ambitious objectives of producing some full
internet based structural health monitoring project with
potential applications to buildings, hospitals and of course,
the collection of bridges monitored by the Ministry of
Transportation of British Columbia. This work is performed
with help of DDS, Belgium and SVIBS, DK. This will implement
INRIA algorithms in a SHM system, and will provide a large
scale outdoor demonstration for I4S. I4S is subcontractor of
SVS. Contract has to be signed.
PhD CIFRE with Dassault Aviation
Laurent
Mevel
Following the FliTE2 project, discussions are under way
about a joint PhD thesis between INRIA and Dassault Aviation.
The thesis will pursue the work achieved in FliTE2 and starts
in January 2011 funded by Dassault Aviation.
SNECMA
Maurice
Goursat
Laurent
Mevel
Contracts INRIA signed in December 2009 (2009-alloc 4589)
and July 2010 (2010-alloc 5110).
In 2007, I4S has investigated for SNECMA an identification
case study on some undisclosed engine structure. Successful
results yield to the delivery of the COSMAD toolbox for
internal evaluation at SNECMA. The end goal is the use of
COSMAD in the industrial process of SNECMA. Internal
evaluation of COSMAD has been performed inhouse by SNECMA in
2008. A contract has been signed and some software package
will be developed to suit SNECMA needs in 2010. Work on the
SNECMA prototype has been performed in 2009 and 2010.
SVIBS
Laurent
Mevel
Michael
Döhler
Annual agreement INRIA-SVIBS 2381 + contract 4329
SVIBS (Structural Vibration Solutions A/S) is a company
located in Aalborg, Denmark, having strong connections with
the Department of Civil Engineering of University of British
Columbia, CA (Prof. Carlos Ventura).
SVIBS and I4S are investigating how to link the modal
analysis software ARTeMIS of SVIBS and COSMAD. Through an
annual agreement, I4S gets a license of ARTeMIS in exchange
to offer support for integrating our damage detection
software into SVIBS software and offerings. A contract has
been signed, where I4S provides algorithms and expertise for
integration within a damage detection structural health
monitoring system and SVIBS does the implementation. This
technology transfer has been funded by the ministry of
transportation of British Columbia, Canada. The work is
supervised by UBC, CA. The end product will be a web based
structural health monitoring system for in operation
bridges.
I4S is doing technology transfer towards SVIBS to
implement I4S technologies into ARTEMIS Extractor Pro. This
is done under a royalty agreement between INRIA and SVIBS .
First achievements include the implementation of the so
called Crystal Clear SSI, a subspace variant, with much lower
signal to noise ratio, and whose interest in the mechanical
engineering community is very high. Other I4S algorithms are
currently under review to be integrated within ARTEMIS. SVIBS
and I4S are also related in the related IAPP ISMS and the
SIMS project.
![]() 0, for example a collection of modes and
mode-shapes.
0, for example a collection of modes and
mode-shapes.![]() , where the distribution of the observations (
, where the distribution of the observations (
![]()
![]()
![]() . An
estimating function, for example of the
form :
. An
estimating function, for example of the
form :![]()
![]() for all
for all
![]()
![]()
![]() . In many situations,
. In many situations,
![]() is the gradient of a function to be minimized :
squared prediction error, log-likelihood (up to a sign), ....
For performing model identification on the basis of
observations
(
is the gradient of a function to be minimized :
squared prediction error, log-likelihood (up to a sign), ....
For performing model identification on the basis of
observations
(
![]()
![]() *is the true parameter value, and that
*is the true parameter value, and that
![]() if and only if
if and only if
![]() =
=
![]() *with
*with
![]() *fixed (identifiability condition), then
*fixed (identifiability condition), then
![]() converges towards
converges towards
![]() *. Thanks to the central limit theorem, the vector
*. Thanks to the central limit theorem, the vector
![]() is asymptotically Gaussian with zero mean, with
covariance matrix
is asymptotically Gaussian with zero mean, with
covariance matrix
![]() which can be either computed or estimated. If,
additionally, the matrix
which can be either computed or estimated. If,
additionally, the matrix
![]() is invertible, then using a Taylor expansion and the
constraint
is invertible, then using a Taylor expansion and the
constraint
![]() , the asymptotic normality of the estimate is
obtained :
, the asymptotic normality of the estimate is
obtained :![]()
![]() simply from
simply from
![]() ;
;![]() *when it is time-varying.
*when it is time-varying.![]() 0and a new data record, indicators which automatically
perform :
0and a new data record, indicators which automatically
perform :![]() , and the safe behavior of the process is assumed to
correspond to the parameter value
, and the safe behavior of the process is assumed to
correspond to the parameter value
![]() 0. This parameter often results from a preliminary
identification based on reference data, as in module
.
0. This parameter often results from a preliminary
identification based on reference data, as in module
.![]() ?One manner to address this generally
difficult question is the following. The asymptotic local
approach consists in deciding between the nominal hypothesis
and a
closealternative hypothesis, namely :
?One manner to address this generally
difficult question is the following. The asymptotic local
approach consists in deciding between the nominal hypothesis
and a
closealternative hypothesis, namely :![]()
![]() is an unknown but fixed change vector. A residual is
generated under the form :
is an unknown but fixed change vector. A residual is
generated under the form :![]()
![]() converges towards a limit
converges towards a limit
![]() , then the central limit theorem shows
that the residual is
asymptotically Gaussian :
, then the central limit theorem shows
that the residual is
asymptotically Gaussian :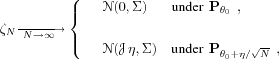
![]() can be estimated, and manifests the deviation in the
parameter vector by a change in its own mean value. Then,
deciding between
can be estimated, and manifests the deviation in the
parameter vector by a change in its own mean value. Then,
deciding between
![]() = 0and
= 0and
![]()
![]() 0amounts to compute the following
0amounts to compute the following
![]() 2-test, provided that
2-test, provided that
![]() is full rank and
is full rank and
![]() is invertible :
is invertible :![]()
![]()
![]() and
and
![]() can be evaluated (or estimated) for the nominal model.
In particular, it is
notnecessary to re-identify the model, and the
sensitivity and covariance matrices can be pre-computed
off-line.
can be evaluated (or estimated) for the nominal model.
In particular, it is
notnecessary to re-identify the model, and the
sensitivity and covariance matrices can be pre-computed
off-line.![]() have been affected by the change. Solutions for that
are now described. How this relates to diagnostics is
addressed afterwards.
have been affected by the change. Solutions for that
are now described. How this relates to diagnostics is
addressed afterwards.![]() have changed ?, can be addressed using either
nuisance parameters elimination methods or a multiple
hypotheses testing approach
. Here we only sketch two
intuitively simple statistical nuisance elimination
techniques, which proceed by projection and rejection,
respectively.
have changed ?, can be addressed using either
nuisance parameters elimination methods or a multiple
hypotheses testing approach
. Here we only sketch two
intuitively simple statistical nuisance elimination
techniques, which proceed by projection and rejection,
respectively.![]() is partitioned into an informative part and a
nuisance part, and the sensitivity matrix
is partitioned into an informative part and a
nuisance part, and the sensitivity matrix
![]() , the Fisher information matrix
, the Fisher information matrix
![]() and the normalized residual
and the normalized residual
![]() are partitioned accordingly
are partitioned accordingly![]()
![]() onto the subspace generated by the components
onto the subspace generated by the components
![]()
![]()
![]()
![]()
![]() 0,
0,
![]()
![]()
![]() is the partial residual (score). If
is the partial residual (score). If
![]()
![]()
![]()
![]()
![]()
![]()
![]() 0, with
0, with
![]()
![]()
![]() is the effective residual (score) resulting from the
regression of the informative partial score
is the effective residual (score) resulting from the
regression of the informative partial score
![]() over the nuisance partial score
over the nuisance partial score
![]() , and where the Schur complement
, and where the Schur complement
![]() is the associated Fisher information matrix. If
is the associated Fisher information matrix. If
![]()
![]() has to be monitored using a simple (black-box) model
characterized by an identifiable parameter vector
has to be monitored using a simple (black-box) model
characterized by an identifiable parameter vector
![]() . A typical example is the vibration monitoring
problem in module
, for which complex finite
elements models are often available but not identifiable,
whereas the small number of existing sensors calls for
identifying only simplified input-output (black-box)
representations. In such a situation, two different
diagnosis problems may arise, namely diagnosis in terms of
the black-box parameter
. A typical example is the vibration monitoring
problem in module
, for which complex finite
elements models are often available but not identifiable,
whereas the small number of existing sensors calls for
identifying only simplified input-output (black-box)
representations. In such a situation, two different
diagnosis problems may arise, namely diagnosis in terms of
the black-box parameter
![]() and diagnosis in terms of the parameter vector
and diagnosis in terms of the parameter vector
![]() of the underlying physical model.
of the underlying physical model.![]() , where
, where
![]() is the Jacobian matrix at
is the Jacobian matrix at
![]() 0of the application
0of the application
![]() , and to use the sensitivity test (
) for the components of the
parameter vector
, and to use the sensitivity test (
) for the components of the
parameter vector
![]() . Typically this results in the following type of
directional test :
. Typically this results in the following type of
directional test :![]()
![]() for the physical model may have a non negligible
influence on such type of tests, according to the numerical
conditioning of the Jacobian matrices
for the physical model may have a non negligible
influence on such type of tests, according to the numerical
conditioning of the Jacobian matrices
![]() .
.![]() of the state transition matrix
of the state transition matrix
![]()
![]() defined by :
defined by :![]()
![]()
![]() is the vector whose elements are the eigenvalues
is the vector whose elements are the eigenvalues
![]() ,
,
![]() is the matrix whose columns are the
is the matrix whose columns are the
![]() 's, and
vecis the column stacking
operator.
's, and
vecis the column stacking
operator.![]() and:
and: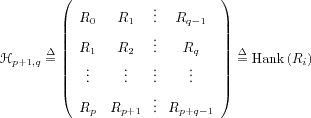
![]() . Direct computations of the
. Direct computations of the
![]()
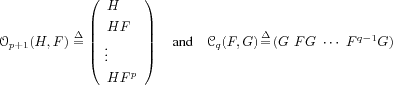
![]() . The state-transition matrix
. The state-transition matrix
![]() . The eigenstructure
. The eigenstructure
![]() then results from (
).
then results from (
).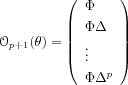
![]() , and
, and
![]() and
and
![]() are as in (
). Whether a nominal
parameter
are as in (
). Whether a nominal
parameter
![]() 0fits a given output covariance sequence
(
0fits a given output covariance sequence
(
![]()
![]() 0, compute
0, compute
![]() using (
), and perform e.g. a singular
value decomposition (SVD) of
using (
), and perform e.g. a singular
value decomposition (SVD) of
![]() for extracting a matrix
for extracting a matrix
![]()
![]() 0. Then the characterization writes:
0. Then the characterization writes:![]()
![]() 0and a new sample
0and a new sample
![]() are available.For checking whether the data
agree with
are available.For checking whether the data
agree with
![]() 0, the idea is to compute the empirical Hankel
matrix
0, the idea is to compute the empirical Hankel
matrix
![]() :
:![]()
![]()
![]() be the actual parameter value for the system which
generated the new data sample, and
be the actual parameter value for the system which
generated the new data sample, and
![]() be the expectation when the actual system parameter
is
be the expectation when the actual system parameter
is
![]() . From (
), we know that
. From (
), we know that
![]()
![]() 0)has zero mean when no change occurs in
0)has zero mean when no change occurs in
![]() , and nonzero mean if a change occurs. Thus
, and nonzero mean if a change occurs. Thus
![]()
![]() 0)plays the role of a residual.
0)plays the role of a residual.![]() in (
), and for deriving the
residual. Factorization (
) is also the key
for :
in (
), and for deriving the
residual. Factorization (
) is also the key
for :