Overall Objectives
Presentation
Algorithmic number theory dates back to the dawn of
mathematics itself,
cf.Eratosthenes's sieve to enumerate consecutive prime
numbers. With the arrival of computers, previously unsolvable
problems have come into reach, which has boosted the
development of more or less practical algorithms for
essentially all number theoretic problems. The field is now
mature enough for a more computer science driven approach,
taking into account the theoretical complexities and
practical running times of the algorithms.
Concerning the lower level multiprecision arithmetic,
folklore has asserted for a long time that asymptotically
fast algorithms such as Schönhage–Strassen multiplication are
impractical; nowadays, however, they are used routinely. On a
higher level, symbolic computation provides numerous
asymptotically fast algorithms (such as for the simultaneous
evaluation of a polynomial in many arguments or linear
algebra on sparse matrices), which have only partially been
exploited in computational number theory. Moreover, precise
complexity analyses do not always exist, nor do sound studies
to choose between different algorithms (an exponential
algorithm may be preferable to a polynomial one for a large
range of inputs); folklore cannot be trusted in a fast moving
area such as computer science.
Another problem is the reliability of the computations;
many number theoretic algorithms err with a small
probability, depend on unknown constants or rely on a Riemann
hypothesis. The correctness of their output can either be
ensured by a special design of the algorithm itself (slowing
it down) or by an
a posterioriverification. Ideally, the algorithm
outputs a certificate, providing an independent
fastcorrectness proof. An example is integer
factorisation, where factors are hard to obtain but trivial
to check; primality proofs have initiated sophisticated
generalisations.
One of the long term goals of the
Lfantproject team
is to make an inventory of the major number theoretic
algorithms, with an emphasis on algebraic number theory and
arithmetic geometry, and to carry out complexity analyses. So
far, most of these algorithms have been designed and tested
over number fields of small degree and scale badly. A
complexity analysis should naturally lead to improvements by
identifying bottlenecks, systematically redesigning and
incorporating modern asymptotically fast methods.
Reliability of the developed algorithms is a second long
term goal of our project team. Short of proving the Riemann
hypothesis, this could be achieved through the design of
specialised, slower algorithms not relying on any unproven
assumptions. We would prefer, however, to augment the fastest
unproven algorithms with the creation of independently
verifiable certificates. Ideally, it should not take longer
to check the certificate than to generate it.
All theoretical results are complemented by concrete
reference implementations in
Pari/Gp, which
allow to determine and tune the thresholds where the
asymptotic complexity kicks in and help to evaluate practical
performances on problem instances provided by the research
community. Another important source for algorithmic problems
treated by the
Lfantproject team
is modern cryptology. Indeed, the security of all practically
relevant public key cryptosystems relies on the difficulty of
some number theoretic problem; on the other hand,
implementing the systems and finding secure parameters
require efficient algorithmic solutions to number theoretic
problems.
Highlights
P. Molin has defended his PhD thesis on “Intégration
numérique et calculs de fonctions
L”
Scientific Foundations
Number fields, class groups and other
invariants
Bill
Allombert
Karim
Belabas
Jean-François
Biasse
Jean-Paul
Cerri
Henri
Cohen
Jean-Marc
Couveignes
Andreas
Enge
Pierre
Lezowski
Pascal
Molin
Anna
Morra
Modern number theory has been introduced in the second
half of the 19th century by Dedekind, Kummer, Kronecker,
Weber and others, motivated by Fermat's conjecture: There is
no non-trivial solution in integers to the equation
xn+
yn=
znfor
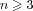 . For recent textbooks, see
. For recent textbooks, see
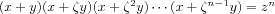 for a primitive
for a primitive
n-th root of unity
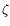 , which seems to imply that each factor on the left
hand side is an
, which seems to imply that each factor on the left
hand side is an
n-th power, from which a contradiction can be
derived.
The solution requires to augment the integers by
algebraic numbers, that are roots of polynomials in
![Im3 ${\#8484 [X]}$](math_image_3.png) . For instance,
. For instance,
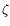 is a root of
is a root of
Xn-1,
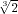 is a root of
is a root of
X3-2and
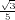 is a root of
25
is a root of
25
X
2-3. A
number fieldconsists of the rationals to which have
been added finitely many algebraic numbers together with
their sums, differences, products and quotients. It turns out
that actually one generator suffices, and any number field
Kis isomorphic to
![Im6 ${\#8474 [X]/(f(X))}$](math_image_6.png) , where
, where
f(
X)is the minimal polynomial of the
generator. Of special interest are
algebraic integers, “numbers without denominators”,
that are roots of a monic polynomial. For instance,
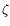 and
and
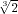 are integers, while
are integers, while
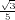 is not. The
ring of integersof
is not. The
ring of integersof
Kis denoted by
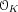 ; it plays the same role in
; it plays the same role in
Kas
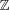 in
in
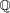 .
.
Unfortunately, elements in
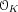 may factor in different ways, which invalidates
Kummer's argumentation. Unique factorisation may be recovered
by switching to
ideals, subsets of
may factor in different ways, which invalidates
Kummer's argumentation. Unique factorisation may be recovered
by switching to
ideals, subsets of
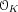 that are closed under addition and under
multiplication by elements of
that are closed under addition and under
multiplication by elements of
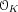 . In
. In
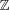 , for instance, any ideal is
principal, that is, generated by one element, so that
ideals and numbers are essentially the same. In particular,
the unique factorisation of ideals then implies the unique
factorisation of numbers. In general, this is not the case,
and the
class group
Cl
, for instance, any ideal is
principal, that is, generated by one element, so that
ideals and numbers are essentially the same. In particular,
the unique factorisation of ideals then implies the unique
factorisation of numbers. In general, this is not the case,
and the
class group
Cl
Kof ideals of
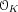 modulo principal ideals and its
class number
modulo principal ideals and its
class number
hK= |Cl
K|measure how far
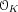 is from behaving like
is from behaving like
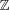 .
.
Using ideals introduces the additional difficulty of
having to deal with
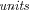 , the invertible elements of
, the invertible elements of
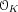 : Even when
: Even when
hK= 1, a factorisation of ideals does not
immediately yield a factorisation of numbers, since ideal
generators are only defined up to units. For instance, the
ideal factorisation
(6) = (2)·(3)corresponds to the two
factorisations
6 = 2·3and
6 = (-2)·(-3). While in
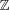 , the only units are 1 and
-1, the unit structure in general
is that of a finitely generated
, the only units are 1 and
-1, the unit structure in general
is that of a finitely generated
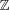 -module, whose generators are the
fundamental units. The
regulator
-module, whose generators are the
fundamental units. The
regulator
RKmeasures the “size” of the fundamental units as the
volume of an associated lattice.
One of the main concerns of algorithmic algebraic number
theory is to explicitly compute these invariants (
Cl
Kand
hK, fundamental units and
RK), as well as to provide the data allowing to
efficiently compute with numbers and ideals of
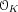 ; see
; see
The
analytic class number formulalinks the invariants
hKand
RK(unfortunately, only their product) to the
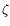 -function of
-function of
K,
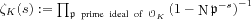 , which is meaningful when
, which is meaningful when
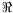 (
(
s)>1, but which may be extended
to arbitrary complex
s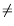 1.
Introducing characters on the class group yields a
generalisation of
1.
Introducing characters on the class group yields a
generalisation of
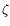 - to
- to
L-functions. The
generalised Riemann hypothesis (GRH), which remains
unproved even over the rationals, states that any such
L-function does not vanish in the right half-plane
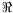 (
(
s)>1/2. The validity of the GRH
has a dramatic impact on the performance of number theoretic
algorithms. For instance, under GRH, the class group admits a
system of generators of polynomial size; without GRH, only
exponential bounds are known. Consequently, an algorithm to
compute
Cl
Kvia generators and relations (currently the only
viable practical approach) either has to assume that GRH is
true or immediately becomes exponential.
When
hK= 1the number field
Kmay be norm-Euclidean, endowing
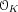 with a Euclidean division algorithm. This question
leads to the notions of the Euclidean minimum and spectrum of
with a Euclidean division algorithm. This question
leads to the notions of the Euclidean minimum and spectrum of
K, and another task in algorithmic number theory is to
compute explicitly this minimum and the upper part of this
spectrum, yielding for instance generalised Euclidean gcd
algorithms.
Function fields, algebraic curves and
cryptology
Karim
Belabas
Jean-François
Biasse
Jean-Marc
Couveignes
Andreas
Enge
Jérôme
Milan
Pascal
Molin
Damien
Robert
Pieter
Rozenhart
Vincent
Verneuil
Algebraic curves over finite fields are used to build the
currently most competitive public key cryptosystems. Such a
curve is given by a bivariate equation
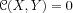 with coefficients in a finite field
with coefficients in a finite field
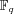 . The main classes of curves that are interesting from
a cryptographic perspective are
elliptic curvesof equation
. The main classes of curves that are interesting from
a cryptographic perspective are
elliptic curvesof equation
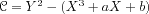 and
hyperelliptic curvesof equation
and
hyperelliptic curvesof equation
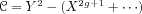 with
with
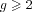 .
.
The cryptosystem is implemented in an associated finite
abelian group, the
Jacobian
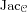 . Using the language of function fields exhibits a
close analogy to the number fields discussed in the previous
section. Let
. Using the language of function fields exhibits a
close analogy to the number fields discussed in the previous
section. Let
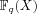 (the analogue of
(the analogue of
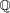 ) be the
rational function fieldwith subring
) be the
rational function fieldwith subring
![Im19 ${\#120125 _q{[X]}}$](math_image_19.png) (which is principal just as
(which is principal just as
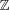 ). The
function fieldof
). The
function fieldof
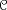 is
is
![Im21 ${K_\#119966 =\#120125 _q{(X)}{[Y]}/{(\#119966 )}}$](math_image_21.png) ; it contains the
coordinate ring
; it contains the
coordinate ring
![Im22 ${\#119978 _\#119966 =\#120125 _q{[X,Y]}/{(\#119966 )}}$](math_image_22.png) . Definitions and properties carry over from the
number field case
. Definitions and properties carry over from the
number field case
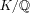 to the function field extension
to the function field extension
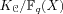 . The Jacobian
. The Jacobian
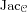 is the divisor class group of
is the divisor class group of
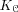 , which is an extension of (and for the curves used in
cryptography usually equals) the ideal class group of
, which is an extension of (and for the curves used in
cryptography usually equals) the ideal class group of
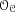 .
.
The size of the Jacobian group, the main security
parameter of the cryptosystem, is given by an
L-function. The GRH for function fields, which has been
proved by Weil, yields the Hasse–Weil bound
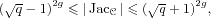 or
or
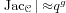 , where the
genus
, where the
genus
gis an invariant of the curve that correlates with the
degree of its equation. For instance, the genus of an
elliptic curve is 1, that of a hyperelliptic one is
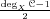 . An important algorithmic question is to compute the
exact cardinality of the Jacobian.
. An important algorithmic question is to compute the
exact cardinality of the Jacobian.
The security of the cryptosystem requires more precisely
that the
discrete logarithm problem(DLP) be difficult in the
underlying group; that is, given elements
D1and
D2=
xD1of
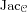 , it must be difficult to determine
, it must be difficult to determine
x. Computing
xcorresponds in fact to computing
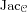 explicitly with an isomorphism to an abstract product
of finite cyclic groups; in this sense, the DLP amounts to
computing the class group in the function field setting.
explicitly with an isomorphism to an abstract product
of finite cyclic groups; in this sense, the DLP amounts to
computing the class group in the function field setting.
For any integer
n, the
Weil pairing
enon
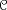 is a function that takes as input two elements of
order
is a function that takes as input two elements of
order
nof
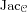 and maps them into the multiplicative group of a
finite field extension
and maps them into the multiplicative group of a
finite field extension
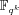 with
with
k=
k(
n)depending on
n. It is bilinear in both its arguments, which allows
to transport the DLP from a curve into a finite field, where
it is potentially easier to solve. The
Tate-Lichtenbaum pairing, that is more difficult to
define, but more efficient to implement, has similar
properties. From a constructive point of view, the last few
years have seen a wealth of cryptosystems with attractive
novel properties relying on pairings.
For a random curve, the parameter
kusually becomes so big that the result of a pairing
cannot even be output any more. One of the major algorithmic
problems related to pairings is thus the construction of
curves with a given, smallish
k.
Complex multiplication
Karim
Belabas
Henri
Cohen
Jean-Marc
Couveignes
Andreas
Enge
Damien
Robert
Complex multiplication provides a link between number
fields and algebraic curves; for a concise introduction in
the elliptic curve case, see
[Sect. 1.1], for more
background material,
 over a finite field, the endomorphism ring of
over a finite field, the endomorphism ring of
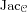 , which determines its
, which determines its
L-function and thus its cardinality, is an order in a
special kind of number field
K, called
CM field. The CM field of an elliptic curve is an
imaginary-quadratic field
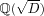 with
with
D<0, that of a hyperelliptic
curve of genus
gis an imaginary-quadratic extension of a totally real
number field of degree
g. Deuring's lifting theorem ensures that
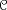 is the reduction modulo some prime of a curve with the
same endomorphism ring, but defined over the
Hilbert class field
is the reduction modulo some prime of a curve with the
same endomorphism ring, but defined over the
Hilbert class field
HKof
K.
Algebraically,
HKis defined as the maximal unramified abelian extension
of
K; the Galois group of
HK/
Kis then precisely the class group
Cl
K. A number field extension
H/
Kis called
Galoisif
![Im32 ${H\#8771 K[X]/(f)}$](math_image_32.png) and
and
Hcontains all complex roots of
f. For instance,
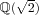 is Galois since it contains not only
is Galois since it contains not only
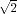 , but also the second root
, but also the second root
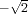 of
of
X2-2, whereas
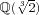 is not Galois, since it does not contain the root
is not Galois, since it does not contain the root
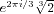 of
of
X3-2. The
Galois group
Gal
H/
Kis the group of
automorphisms of
Hthat fix
K; it permutes the roots of
f. Finally, an
abelianextension is a Galois extension with abelian
Galois group.
Analytically, in the elliptic case
HKmay be obtained by adjoining to
Kthe
singular value
j(
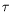 )for a
complex valued, so-called
modularfunction
)for a
complex valued, so-called
modularfunction
jin some
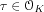 ; the correspondence between
Gal
; the correspondence between
Gal
H/
Kand
Cl
Kallows to obtain the different roots of the
minimal polynomial
fof
j(
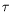 )and
finally
)and
finally
fitself. A similar, more involved construction can be
used for hyperelliptic curves. This direct application of
complex multiplication yields algebraic curves whose
L-functions are known beforehand; in particular, it is
the only possible way of obtaining ordinary curves for
pairing-based cryptosystems.
The same theory can be used to develop algorithms that,
given an arbitrary curve over a finite field, compute its
L-function.
A generalisation is provided by
ray class fields; these are still abelian, but allow
for some well-controlled ramification. The tools for
explicitly constructing such class fields are similar to
those used for Hilbert class fields.
Application Domains
Number theory
Being able to compute quickly and reliably algebraic
invariants is an invaluable aid to mathematicians: It fosters
new conjectures, and often shoots down the too optimistic
ones. Moreover, a large body of theoretical results in
algebraic number theory has an asymptotic nature and only
applies for large enough inputs; mechanised computations
(preferably producing independently verifiable certificates)
are often necessary to finish proofs.
For instance, many Diophantine problems reduce to a set of
Thue equations of the form
P(
x,
y) =
afor an irreducible, homogeneous
![Im39 ${P\#8712 \#8484 [x,y]}$](math_image_39.png) ,
,
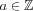 , in unknown integers
, in unknown integers
x,
y. In principle, there is an
algorithm to solve the latter, provided the class group and
units of a rupture field of
Pare known. Since there is no other way to prove that
the full set of solutions is obtained, these algebraic
invariants must be computed and certified, preferably without
using the GRH.
Deeper invariants such as the Euclidean spectrum are
related to more theoretical concerns, e.g., determining
new examples of principal, but not norm-Euclidean number
fields, but could also yield practical new algorithms: Even
if a number field has class number larger than 1 (in
particular, it is not norm-Euclidean), knowing the upper part
of the spectrum should give a
partialgcd algorithm, succeeding for almost all pairs
of elements of
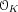 . As a matter of fact, every number field which is not
a complex multiplication field and whose unit group has rank
strictly greater than 1 is almost norm-Euclidean
. As a matter of fact, every number field which is not
a complex multiplication field and whose unit group has rank
strictly greater than 1 is almost norm-Euclidean
Algorithms developed by the team are implemented in the
free
Pari/Gpsystem for
number theory maintained by K. Belabas, which is a
reference and the tool of choice for the worldwide number
theory community.
Cryptology
Public key cryptology has become a major application
domain for algorithmic number theory. This is already true
for the ubiquitous RSA system, but even more so for
cryptosystems relying on the discrete logarithm problem in
algebraic curves over finite fields
Apart from solving specific problems related to
cryptology, number theoretic expertise is vital to provide
cryptologic advice to industrial partners in joint projects.
It is to be expected that continuing pervasiveness and
ubiquity of very low power computing devices will render the
need for algebraic curve cryptography more pressing in coming
years.
Software
Pari/Gp
Karim
Belabas
correspondant
Bill
Allombert
Henri
Cohen
Andreas
Enge
[http://
pari.
math.
u-bordeaux.
fr/
]
License: GPL 2+
Current stable version of
Pari/Gp: 2.3.5,
2010
Current testing version of
Pari/Gp:
2.4.3.alpha, 2010
Current version of
gp2c: 0.0.5pl10, 2010
Pari/Gpis a widely
used computer algebra system designed for fast computations
in number theory (factorisation, algebraic number theory,
elliptic curves, ...), but it also contains a large number of
other useful functions to compute with mathematical entities
such as matrices, polynomials, power series, algebraic
numbers, etc., and many transcendental functions.
Pariis a C
library, allowing fast computations.
Gpis an
easy-to-use interactive shell giving access to the
Parifunctions.
gp2c, the GP-to-C compiler, combines the best of
both worlds by compiling
Gpscripts to
the C language and transparently loading the resulting
functions into
Gp; scripts
compiled by
gp2cwill typically run three to four times
faster.
Mpc
Andreas
Enge
correspondant
Philippe
Théveny
Paul
Zimmermann
Inriaproject-team
Caramel
[http://
mpc.
multiprecision.
org/
]
License: LGPL 2.1+
Current version: 0.8.2
Dianthus deltoides, 2010
Mpcis a C library
for the arithmetic of complex numbers with arbitrarily high
precision and correct rounding of the result. It is built
upon and follows the same principles as
Mpfr. The
Mpclibrary has
been registered in France by the Agence pour la Protection
des Programmes on 2003-02-05 under the number IDDN FR 001
060029 000 R P 2003 000 10000.
It is a prerequisite for the release 4.5 of the
Gnucompiler
collection
Gcc, where it is
used in the C and Fortran frontends for constant folding, the
evaluation of constant mathematical expressions during the
compilation of a program.
Mpfrcx
Andreas
Enge
[http://
mpfrcx.
multiprecision.
org/
]
License: LGPL 2.1+
Current version: 0.3.1
Banane, 2010
Mpfrcxis a library
for the arithmetic of univariate polynomials over arbitrary
precision real (
Mpfr) or complex (
Mpc) numbers,
without control on the rounding. For the time being, only the
few functions needed to implement the floating point approach
to complex multiplication are implemented. On the other hand,
these comprise asymptotically fast multiplication routines
such as Toom-Cook and the FFT.
Cm
Andreas
Enge
[http://
cm.
multiprecision.
org/
]
License: GPL 2+
Initial public release: version 0.1
Apfelkraut, 2009
The
Cmsoftware
implements the construction of ring class fields of imaginary
quadratic number fields and of elliptic curves with complex
multiplication via floating point approximations. It consists
of libraries that can be called from within a C program and
of executable command line applications. For the implemented
algorithms, see
Cubic
Karim
Belabas
[http://
www.
math.
u-bordeaux.
fr/
~belabas/
research/
software/
cubic-1.
0.
tgz]
License: GPL 2+
Current stable version: 1.0, 2009
Cubicis a
standalone program that prints out generating equations for
cubic fields of either signature and bounded discriminant. It
depends on the
Parilibrary. The
algorithm has quasi-linear time complexity in the size of the
output.
New Results
Discrete logarithms
Andreas
Enge
In
L(1/2), namely,
L(1/3 +
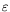 )for any
)for any
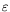 >0. In
>0. In
L(1/3), showing that the
corresponding algebraic curves (essentially
Cabcurves of genus
ggrowing at least quadratically with the logarithmic
size of the finite field of definition,
log
q) result in cryptosystems that are
as easily attacked as RSA or tradtional cryptosystems based
on discrete logarithms in finite fields. We provide a
complete classification of all the curves to which the attack
applies. The article has been accepted by
Journal of Cryptology.
Class groups and other invariants of number
fields
Bill
Allombert
Karim
Belabas
Jean-François
Biasse
Jean-Paul
Cerri
Pierre
Lezowski
J.-F. Biasse has made practical improvements to the
sieving-based algorithm of Jacobson
He has also determined a class of number fields for which
the ideal class group, the regulator, and a system of
fundamental units of the maximal order can be computed in
subexponential time
L(1/3,
O(1))(whereas the best previously
known algorithms have complexity
L(1/2,
O(1))). This class of number fields
is analogous to the class of curves described in
In collaboration with M. Jacobson, J.-F. Biasse
has described improvements to the sieving methods for ideal
class group, regulator and fundamental unit computation
Together with M. Jacobson and A. Silvester,
J.-F. Biasse has improved the algorithms for solving the
discrete logarithm problem and the principal ideal problem,
which are involved in the design of cryptosystems based on
number fields
Using new theoretical ideas and his novel algorithmic
approach, J.-P. Cerri has discovered examples of
generalised Euclidean number fields and of 2-stage
norm-Euclidean number fields in degree greater
than 2
The algorithms developed by J.-P. Cerri for totally
real fields are currently being generalised by
P. Lezowski to arbitrary number fields.
In collaboration with L. Grenié, B. Allombert
and K. Belabas have considerably improved the practical
efficiency of PARI/GP algorithms computing class and unit
groups, in particular for number fields of large degree. They
are currently working on a flexible parallelisation framework
of the PARI/GP system; a first application target is to
improve the relation finding part of the class group
algorithms (affording in principle a linear speedup).
Number and function field enumeration
Karim
Belabas
Henri
Cohen
Anna
Morra
Pieter
Rozenhart
In joint work with É. Fouvry (Orsay), K. Belabas
has proved a new case of Malle's conjecture, a strong
effective form of the inverse Galois problem
S3, ordered by discriminant, using classical
Davenport-Heilbronn theory in a novel way. The same result
was independently obtained by Bhargava and Wood using a
different method.
In joint work with R. Scheidler and M. Jacobson,
P. Rozenhart has generalized Belabas's algorithm for
tabulating cubic number fields to cubic function fields. This
generalization required function field analogues of the
Davenport-Heilbronn Theorem and of the reduction theory of
binary cubic and quadratic forms. As an additional
application, they have modified the tabulation algorithm to
compute 3-ranks of quadratic function fields by way of a
generalisation of a theorem due to Hasse. The algorithm,
whose complexity is quasi-linear in the number of reduced
binary cubic forms up to some upper bound
X, works very well in practice. The article
H. Cohen and A. Morra have obtained an explicit
expression for the Dirichlet generating function associated
to cubic extensions of an arbitrary number field with a fixed
quadratic resolvent. As a corollary, they have proved
refinements of Malle's conjecture in this context. The
article
L-functions
Bill
Allombert
Karim
Belabas
Henri
Cohen
Pascal
Molin
Classical theorems of Davenport and Heilbronn enumerate
cubic fields and estimate the average 3-torsion of class
groups of quadratic fields. In joint work with
M. Bhargava (Princeton) and C. Pomerance (Dartmouth
College), K. Belabas has proved the first power-saving
error terms for those results, lending support to a
conjecture of Roberts
s= 1, proving a conjecture of
Cohen. Since then, in the summer of 2010, Bhargava, Shankar
and Tsimerman have proven Roberts's full conjecture.
As for effective computations of general
L-functions, methods have been designed for ten years
and programs due to T. Dokchitser and M. Rubinstein
are available. In his thesis
L-function algorithms in the PARI/GP system with the
help of B. Allombert.
Complex multiplication
Andreas
Enge
With F. Morain, A. Enge has determined exhaustively under
which conditions “generalised Weber functions”, that is,
simple quotients of
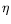 functions of not necessarily prime transformation
level and not necessarily of genus 1, yield class
invariants
functions of not necessarily prime transformation
level and not necessarily of genus 1, yield class
invariants
In
Elliptic curve cryptology
Jérôme
Milan
Vincent
Verneuil
Together with C. Giraud, V. Verneuil has
addressed the problem of protecting elliptic curve scalar
multiplication implementations against side-channel analysis
by using the atomicity principle
In
J. Milan has worked with T. Clausen and
U. Herberg (Hipercom@LIX, École polytechnique) to bring
some basic authentication mechanism to the OLSRv2 routing
protocol in mobile ad-hoc networks by using digital
signatures based on elliptic curves (ECDSA) and pairings on
such curves (BSL-like signature). Such a mechanism has been
developed and integrated within Hipercom@LIX's jOlsrv2
framework, which provides a Java-based implementation of the
OLSRv2 protocol and interfaces with a network simulator (NS2)
Dissemination
Thesis committees
K. Belabas has been a referee for the thesis of
Alexander Kruppa (Nancy, “Speeding up Integer Multiplication
and Factorization”) and Alexander Rahm (Grenoble,
“(Co)homologies and
K-theory of Bianchi groups using computational
geometric models”). He has been a committee member for the
PhD defense of Tony Ezome (Toulouse, “Courbes elliptiques,
cyclotomie et primalité”).
Jean-Marc Couveignes has been a committee member for Luca
De Feo's PhD defense on “Algorithmes rapides pour les tours
de corps finis et les isogénies” at École polytechnique.
A. Enge has taken part in the committee for Thomas
Icart's PhD “Algorithms mapping into elliptic curves and
applications” at Université du Luxemburg.
Editorships
K. Belabas acts on the editorial board of
Journal de Théorie des Nombres de Bordeauxsince 2005
and of
Archiv der Mathematiksince 2006.
H. Cohen is an editorial board member of
Journal de Théorie des Nombres de Bordeaux; he is an
editor for the Springer book series
Algorithms and Computations in Mathematics (ACM).
A. Enge is an editor of
Designs, Codes and Cryptographysince 2004.
Invited talks
A. Enge has given a talk on “Class polynomials by
Chinese remaindering” at ECC 2010 – Workshop on Elliptic
Curves and Computation in Redmond.
P. Rozenhart has presented “Computing quadratic
function fields with high 3-rank via cubic field tabulation”
at the 11th meeting of the Canadian Number Theory
Association. He has given an invited talk at Bates College in
Lewiston, Maine, USA, titled “Computing quadratic function
fields with high 3-rank via cubic field tabulation”.
Conference organisation and programme
committees
We have organised a workshop on the algorithmics of
L-functions from December 6 to 10 at Bordeaux. 18 talks
were programmed during the week, which left ample room for
scientific exchange. In addition to the
Lfantteam members,
the workshop was attended by a dozen of researchers. Two
students from ENS Paris, who intend to pursue a PhD with the
team, took also part.
The first day was dedicated to algorithmics of number
fields; the second, to Iwasawa theory; the third, to theta
functions and arithmetic groups; the fourth, to the search
for rational points on modular curves and the algorithmics of
holomorphic functions. On the last day, we have treated
complex multiplication and
p-adic
L-functions.
The following persons have given a presentation: Bill
Allombert (Bordeaux), Peter Bruin (Orsay), Julien Blondeau
(Besançon), Henri Cohen (Bordeaux), Guillaume Perbet
(Besançon), Christophe Delaunay (Lyon), Damien Robert
(Bordeaux), Aurel Page (ENS Paris), Pierre Parent (Bordeaux),
Marusia Rebolledo (Clermont-Ferrand), Jean-Marc Couveignes
(Bordeaux), Pascal Molin (Nancy), Nicolas Mascot (ENS Paris),
Andreas Enge (Bordeaux), Xavier Roblot (Tokyo).
H. Cohen is a member of the scientific comittee for
ANTS – Algorithmic Number Theory Symposium, the major,
biennial international conference in the field.
A. Enge acts on the scientific advisory board of the
Journées Nationales de Calcul Formel.
Seminar
The following external speakers have given a presentation
at the
Lfantseminar,
see
[http://
www.
math.
u-bordeaux1.
fr/
~enge/
lfant/
index.
php?category=seminar]
Damien Robert: “Calcul de pairings
avec les fonctions thetas”
Damien Robert: “Computing isogenies
between abelian varieties”
Eduardo Friedman: “Special values of
Dirichlet series and Zeta integrals associated to
polynomials”
Loïc Grenié: “Comment vérifier si deux
représentations galoisiennes ont la même
semi-simplifiée”
Michael Drmota: “An asymptotic
analysis of Cuckoo hashing”
Paul Zimmermann: “Peut-on calculer sur
ordinateur?”
Manuel Charlemagne: “The security of
the discrete logarithm problem (DLP) in the context of
pairings”
Damien Bernard: “Petits zéros de
fonctions L associées à un corps quadratique
imaginaire”
Peter Bruin: “Sur le calcul des
coefficients des formes modulaires”
David Lubicz: “Couplage avec les
fonctions thêta”
Teaching
K. Belabas has taught a bachelor course in cryptology, and
master courses on computer algebra, elliptic curves, and the
algorithmic of public key cryptography. He has supervised
master projects on cyclotomic proofs of (cases of) Fermat's
Last Theorem, optimal elliptic curve models for cryptography,
factorisation of univariate polynomials over a finite field,
asymptotically fast integer multiplication (from Karatsuba to
Fürer), and sub-quadratic integer division algorithms.
J.-F. Biasse was a teaching assistant (“moniteur”) at
the Applied Mathematics Department (CMAP) of École
polytechnique. He was involved in the following courses:
Introduction to C++, Numerical Analysis, Probability.
J.-P. Cerri has been in charge during two years of the
course “Computational Number Theory” of the international
research master programme Algant. This year, he teaches
bachelor students working towards the master programme CSI on
cryptology and information security. He is responsable for
running the bachelor programmes in mathematics and computer
science.
A. Enge is a “Chargé d'enseignement” at the Department of
Informatics of École polytechnique. He has taught a master
course on cryptology and a bachelor course on web
programming.
Research administration
K. Belabas is the head of the mathematics department
of University Bordeaux 1. He also leads the computer science
support service (“cellule informatique”) of the Institute of
Mathematics of Bordeaux and coordinates the participation of
the institute in the regional computation cluster
PlaFRIM.
He is an elected member of the councils of both the math
and computer science department (UFR) and the Math Institute
(IMB).
A. Enge has taken part in the hiring committees for
two maîtres de conférences in mathematics at the Universities
of Bordeaux and Caen, and for a CNRS chair in cryptology at
the department of computer science of University of
Versailles.
![]() . For recent textbooks, see
. Kummer's idea for solving
Fermat's problem was to rewrite the equation as
. For recent textbooks, see
. Kummer's idea for solving
Fermat's problem was to rewrite the equation as
![]() for a primitive
for a primitive
![]() , which seems to imply that each factor on the left
hand side is an
, which seems to imply that each factor on the left
hand side is an
![]() . For instance,
. For instance,
![]() is a root of
is a root of
![]() is a root of
is a root of
![]() is a root of
25
is a root of
25
![]() , where
, where
![]() and
and
![]() are integers, while
are integers, while
![]() is not. The
ring of integersof
is not. The
ring of integersof
![]() ; it plays the same role in
; it plays the same role in
![]() in
in
![]() .
.![]() may factor in different ways, which invalidates
Kummer's argumentation. Unique factorisation may be recovered
by switching to
ideals, subsets of
may factor in different ways, which invalidates
Kummer's argumentation. Unique factorisation may be recovered
by switching to
ideals, subsets of
![]() that are closed under addition and under
multiplication by elements of
that are closed under addition and under
multiplication by elements of
![]() . In
. In
![]() , for instance, any ideal is
principal, that is, generated by one element, so that
ideals and numbers are essentially the same. In particular,
the unique factorisation of ideals then implies the unique
factorisation of numbers. In general, this is not the case,
and the
class group
Cl
, for instance, any ideal is
principal, that is, generated by one element, so that
ideals and numbers are essentially the same. In particular,
the unique factorisation of ideals then implies the unique
factorisation of numbers. In general, this is not the case,
and the
class group
Cl
![]() modulo principal ideals and its
class number
modulo principal ideals and its
class number
![]() is from behaving like
is from behaving like
![]() .
.![]() , the invertible elements of
, the invertible elements of
![]() : Even when
: Even when
![]() , the only units are 1 and
-1, the unit structure in general
is that of a finitely generated
, the only units are 1 and
-1, the unit structure in general
is that of a finitely generated
![]() -module, whose generators are the
fundamental units. The
regulator
-module, whose generators are the
fundamental units. The
regulator
![]() ; see
for a recent account.
; see
for a recent account.![]() -function of
-function of
![]() , which is meaningful when
, which is meaningful when
![]() (
(
![]() 1.
Introducing characters on the class group yields a
generalisation of
1.
Introducing characters on the class group yields a
generalisation of
![]() - to
- to
![]() (
(
![]() with a Euclidean division algorithm. This question
leads to the notions of the Euclidean minimum and spectrum of
with a Euclidean division algorithm. This question
leads to the notions of the Euclidean minimum and spectrum of
![]() with coefficients in a finite field
with coefficients in a finite field
![]() . The main classes of curves that are interesting from
a cryptographic perspective are
elliptic curvesof equation
. The main classes of curves that are interesting from
a cryptographic perspective are
elliptic curvesof equation
![]() and
hyperelliptic curvesof equation
and
hyperelliptic curvesof equation
![]() with
with
![]() .
.![]() . Using the language of function fields exhibits a
close analogy to the number fields discussed in the previous
section. Let
. Using the language of function fields exhibits a
close analogy to the number fields discussed in the previous
section. Let
![]() (the analogue of
(the analogue of
![]() ) be the
rational function fieldwith subring
) be the
rational function fieldwith subring
![]() (which is principal just as
(which is principal just as
![]() ). The
function fieldof
). The
function fieldof
![]() is
is
![]() ; it contains the
coordinate ring
; it contains the
coordinate ring
![]() . Definitions and properties carry over from the
number field case
. Definitions and properties carry over from the
number field case
![]() to the function field extension
to the function field extension
![]() . The Jacobian
. The Jacobian
![]() is the divisor class group of
is the divisor class group of
![]() , which is an extension of (and for the curves used in
cryptography usually equals) the ideal class group of
, which is an extension of (and for the curves used in
cryptography usually equals) the ideal class group of
![]() .
.![]() or
or
![]() , where the
genus
, where the
genus
![]() . An important algorithmic question is to compute the
exact cardinality of the Jacobian.
. An important algorithmic question is to compute the
exact cardinality of the Jacobian.![]() , it must be difficult to determine
, it must be difficult to determine
![]() explicitly with an isomorphism to an abstract product
of finite cyclic groups; in this sense, the DLP amounts to
computing the class group in the function field setting.
explicitly with an isomorphism to an abstract product
of finite cyclic groups; in this sense, the DLP amounts to
computing the class group in the function field setting.![]() is a function that takes as input two elements of
order
is a function that takes as input two elements of
order
![]() and maps them into the multiplicative group of a
finite field extension
and maps them into the multiplicative group of a
finite field extension
![]() with
with
![]() over a finite field, the endomorphism ring of
over a finite field, the endomorphism ring of
![]() , which determines its
, which determines its
![]() with
with
![]() is the reduction modulo some prime of a curve with the
same endomorphism ring, but defined over the
Hilbert class field
is the reduction modulo some prime of a curve with the
same endomorphism ring, but defined over the
Hilbert class field
![]() and
and
![]() is Galois since it contains not only
is Galois since it contains not only
![]() , but also the second root
, but also the second root
![]() of
of
![]() is not Galois, since it does not contain the root
is not Galois, since it does not contain the root
![]() of
of
![]() )for a
complex valued, so-called
modularfunction
)for a
complex valued, so-called
modularfunction
![]() ; the correspondence between
Gal
; the correspondence between
Gal
![]() )and
finally
)and
finally