Our conceptual framework is that of Control Theory : the system is described by state variables with inputs (actions on the system) and outputs (the available measurements). Our system is either an epidemiological or immunological system or a harvested fish population. The control theory approach begins with the mathematical modeling of the system. When a “satisfying" model is obtained, this model is studied to understand the system. By “satisfying", an ambiguous word , we mean validation of the model. This depends on the objectives of the design of the model: explicative model, predictive model, comprehension model, checking hypotheses model. Moreover the process of modeling is not sequential. During elaboration of the model, a mathematical analysis is often done in parallel to describe the behavior of the proposed model. By behavior we intend not only asymptotic behavior but also such properties as observability, identifiability, robustness ...
Problems in epidemiology, immunology and virology can be expressed as standard problems in control theory. But interesting new questions do arise. The control theory paradigm, input-output systems built out of simpler components that are interconnected, appears naturally in this context. Decomposing the system into several sub-systems, each of which endowed with certain qualitative properties, allow the behavior of the complete system to be deduced from the behavior of its parts. This paradigm, the toolbox of feedback interconnection of systems, has been used in the so-called theory of large-scale dynamic systems in control theory . Reasons for decomposing are multiple. One reason is conceptual. For example connection of the immune system and the parasitic systems is a natural biological decomposition. Others reasons are for the sake of reducing algorithmic complexities or introducing intended behavior ...In this case subsystems may not have biological interpretation. For example a chain of compartments can be introduced to simulate a continuous delay , . Analysis of the structure of epidemiological and immunological systems is vital because of the paucity of data and the dependence of behavior on biological hypotheses. The issue is to identify those parts of models that have most effects on dynamics. The concepts and techniques of interconnection of systems (large-scale systems) will be useful in this regard.
In mathematical modeling in epidemiology and immunology, as in most other areas of mathematical modeling, there is always a trade-off between simple models, that omit details and are designed to highlight general qualitative behavior, and detailed models, usually designed for specific situations, including short-terms quantitative predictions. Detailed models are generally difficult to study analytically and hence their usefulness for theoretical purposes is limited, although their strategic value may be high. Simple models can be considered as building blocks of models that include detailed structure. The control theory tools of large-scale systems and interconnections of systems is a mean to conciliate the two approaches, simple models versus detailed systems.
Many dynamical questions addressed by Systems Theory are precisely what biologist are asking. One fundamental problem is the problem of equilibria and their stability. To quote J.A. Jacquez
A major project in deterministic modeling of heterogeneous populations is to find conditions for local and global stability and to work out the relations among these stability conditions, the threshold for epidemic take-off, and endemicity, and the basic reproduction number
The basic reproduction number
![]() is an important quantity in the study in epidemics. It
is defined as the average number of secondary infections
produced when one infected individual is introduced into a
host population where everyone is susceptible. The basic
reproduction number
is an important quantity in the study in epidemics. It
is defined as the average number of secondary infections
produced when one infected individual is introduced into a
host population where everyone is susceptible. The basic
reproduction number
![]() is often considered as the threshold quantity that
determines when an infection can invade and persist in a new
host population. To the problem of stability is related the
problem of robustness, a concept from control theory. In
other words how near is the system to an unstable one ?
Robustness is also in relation with uncertainty of the
systems. This is a key point in epidemiological and
immunological systems, since there are many sources of
uncertainties in these models. The model is uncertain
(parameters, functions, structure in some cases), the inputs
also are uncertain and the outputs highly variable. That
robustness is a fundamental issue and can be seen by means of
an example : if policies in public health are to be
taken from modeling, they must be based on robust
reasons!
is often considered as the threshold quantity that
determines when an infection can invade and persist in a new
host population. To the problem of stability is related the
problem of robustness, a concept from control theory. In
other words how near is the system to an unstable one ?
Robustness is also in relation with uncertainty of the
systems. This is a key point in epidemiological and
immunological systems, since there are many sources of
uncertainties in these models. The model is uncertain
(parameters, functions, structure in some cases), the inputs
also are uncertain and the outputs highly variable. That
robustness is a fundamental issue and can be seen by means of
an example : if policies in public health are to be
taken from modeling, they must be based on robust
reasons!
The concept of observer originates in control theory. This is particularly pertinent for epidemiological systems. To an input-output system, is associated the problem of reconstruction of the state. Indeed for a given system, not all the states are known or measured, this is particularly true for biological systems. This fact is due to a lot of reasons : this is not feasible without destroying the system, this is too expensive, there are no available sensors, measures are too noisy ...The problem of knowledge of the state at present time is then posed. An observer is another system, whose inputs are the inputs and the outputs of the original system and whose output gives an estimation of the state of the original system at present time. Usually the estimation is required to be exponential. In other words an observer, using the signal information of the original system, reconstructs dynamically the state. More precisely, consider an input-output nonlinear system described by
![]()
where
![]() is the state of the system at time
is the state of the system at time
t,
![]() is the input and
is the input and
![]() is the measurable output of the system.
is the measurable output of the system.
An observer for the the system ( ) is a dynamical system
![]()
where the map
ghas to be constructed such that: the solutions
x(
t)and
![]() of (
) and (
) satisfy for any initial
conditions
of (
) and (
) satisfy for any initial
conditions
x(0)and
![]()
![]()
or at least
![]() converges to zero as time goes to infinity.
converges to zero as time goes to infinity.
The problem of observers is completely solved for linear time-invariant systems (LTI). This is a difficult problem for nonlinear systems and is currently an active subject of research. The problem of observation and observers (software sensors) is central in nonlinear control theory. Considerable progress has been made in the last decade, especially by the “French school", which has given important contributions (J.P. Gauthier, H. Hammouri, E. Busvelle, M. Fliess, L. Praly, J.L. Gouze, O. Bernard, G. Sallet ) and is still very active in this area. Now the problem is to identify relevant class of systems for which reasonable and computable observers can be designed. The concept of observer has been ignored by the modeler community in epidemiology, immunology and virology. To our knowledge there is only one case of use of an observer in virology ( Velasco-Hernandez J. , Garcia J. and Kirschner D. ) in modeling the chemotherapy of HIV, but this observer, based on classical linear theory, is a local observer and does not allow to deal with the nonlinearities.
Another crucial issue for biological systems is the question of delays. Delays, in control theory, are traditionally discrete (more exactly, the delays are lags) whereas in biology they usually are continuous and distributed. For example, the entry of a parasite into a cell initiates a cascade of events that ultimately leads to the production of new parasites. Even in a homogeneous population of cells, it is unreasonable to expect that the time to complete all these processes is the same for every cell. If we furthermore consider differences in cell activation state, metabolism, position in the cell cycle, pre-existing stores of nucleotides and other precursors needed for the reproduction of parasites, along with genetic variations in the parasite population, such variations in infection delay times becomes a near certainty. The rationale for studying continuous delays are supported by such considerations. In the literature on dynamical systems, we find a wealth of theorems dealing with delay differential equations. However they are difficult to apply. Control theory approaches (interconnections of systems), is a mean to study the influence of continuous delays on the stability of such systems. We have obtained some results in this direction .
We are considering general classes of models to address some epidemiological peculiarity. For example we consider and analyze a class of models , under the general form
![]()
where
![]() represents the concentration of susceptible
individuals or target cells,
represents the concentration of susceptible
individuals or target cells,
![]() represents the different class of latent, infectious
and removed individuals. The matrix
represents the different class of latent, infectious
and removed individuals. The matrix
Cis a nonzero
k×
nnonnegative matrix,
![]() is a positive vector,
is a positive vector,
Pdenotes a linear projection,
Ais a stable Metzler matrix and
![]() denotes a scalar product in
denotes a scalar product in
![]() . The function
. The function
![]() describes the recruitment (or the demography) of
susceptible individuals or cells and the quantity
describes the recruitment (or the demography) of
susceptible individuals or cells and the quantity
![]() represents the infection transmission. For some
diseases, a bilinear infection transmission function
represents the infection transmission. For some
diseases, a bilinear infection transmission function
![]() is not adequate so we have to replace in equation (
) the expression
is not adequate so we have to replace in equation (
) the expression
Cyby a more general non-linear incidence function
Cf(
y). The parameter
utakes only the value 0 or 1.
The model (
) represents either the
transmission of a directly transmitted disease (i.e
transmitted by adequate contact, Ebola, Tuberculosis, ...),
in this case
u= 0, or represents the
intra-host dynamics of a parasite with target cells. To
illustrate this claim we will give two examples.
The system (
) can represent the so called
DI, SP or DISP models. In the studies of the transmission
dynamics of HIV, two fundamental hypotheses for variations
in infectiousness have been made. In the staged-progression
(SP) hypothesis, the infected individuals sequentially pass
through a serie of stages, being highly infectious in the
first few weeks after their own infection, then having low
infectivity for many years, and finally becoming gradually
more infectious as their immune system breaks down and they
progress to AIDS. Based on other clinic findings and blood
serum level studies, another hypothesis is the differential
infectivity (DI) hypothesis, where infected individuals
enter one of several groups
j(
j= 1...
n) with probability
![]()
j, depending on their infectivity, and stay in that
group until they develop AIDS. If we denote by
Sthe density of susceptible individuals,
Iithe density of the different classes of infectious
individuals, the DI model can be represented by a
compartmental model:
which gives the differential equation
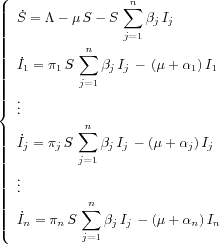
where
![]() is an input flow (or a recruitment rate) which is
supposed to be constant,
is an input flow (or a recruitment rate) which is
supposed to be constant,
![]() is the natural death rate of the population. For
each
is the natural death rate of the population. For
each
jthe parameter
![]()
jis the contact rate, i.e., the rate at which
susceptibles meet infectious individuals belonging to the
class
j, the parameter
![]()
jis the disease-related death rate of the class
jand
![]()
Similarly the SP model can be represented by
The parameter
![]()
jdenotes the fractional rate of transfer of infected
from the stage
jto the stage
j+ 1. The dynamical progression
of the disease can be represented by the differential
equation:
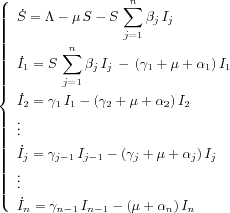
The DISP is the combination of these two structures. These models are easily put under the general form. ( ).
This general form can also represents intra-host models : We sketch the example of malaria . We give a brief review of the biological features of malaria. Malaria in a human begins with an inoculum of Plasmodiumparasites (sporozoites) from a female Anophelesmosquito. The sporozoites enter the liver within minutes. After a period of asexual reproduction in the liver, the parasites (merozoites) are released in the bloodstream where the asexual erythrocyte cycle begins. The merozoites enter red blood cells (RBC), grow and reproduce over a period of approximately 48 hours after which the erythrocyte ruptures releasing daughter parasites that quickly invade a fresh erythrocyte to renew the cycle. This blood cycle can be repeated many times, in the course of which some of the merozoites instead develop in the sexual form of the parasites : gametocytes. Gametocytes are benign for the host and are waiting for the mosquitoes. An important characteristic of Plasmodium falciparum, the most virulent malaria parasite, is sequestration. At the half-way point of parasite development, the infected erythrocyte leaves the circulating peripheral blood and binds to the endothelium in the microvasculature of various organs where the cycle is completed. A measurement of Plasmodium falciparumparasitaemia taken from a blood smear therefore samples young parasites only. Physician treating malaria use the number of parasites in peripheral blood smears as a measure of infection, this does not give the total parasite burden of the patient. Moreover antimalarial drugs are known to act preferentially on different stages of parasite development. Hence to model the dynamics of parasitized erythrocytes, it is natural to introduce different classes. Then we propose the following model
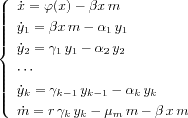
where the variable
xdenotes the concentration of uninfected RBC, the
variable
yjis the concentration of parasitized red blood cell
(PRBC) of class
j, and
mis the concentration of the free merozoites in the
blood. The example of malaria gives an example where stages
in modeling are created for biological reasons. We have
seen before that continuous delays are important to be
modeled. The process of converting time-delay
integro-differential equations in a set of ODE is coined by
MacDonald
as the linear chain trick. In
other community this is also known as the method of stages.
Actually any distribution can be approximated by a
combination of stages in series and in parallel (Jacquez).
This process consists to insert stages in the model. This
is an example of stages created to take into account a
behavior. This added stages have no biological meaning. Our
general model is also well suited for this process.
The general model ( ) can take into account the case of different strains for the parasites and can be adapted to cope with vector transmitted diseases. Then we have a building block to model complex systems. System ( ) describes the basic model which can be extended, by introducing interconnections of blocks of the form ( ), to describe more complex systems : more classes of susceptible can be introduced, the recruitment of susceptible individuals can be replaced by an output of an explicit model of the population dynamics, each sub-system describes what happens in a patch, inflows and outflows can be introduced to model the population movement between patches, different strains for the pathogen can be introduced, others systems can bring input in these models (e.g. the immune system) ...
This general form will be used to
model some well-identified diseases for which we have data
and expert collaborators (e.g. malaria, dengue, Ebola ...).
This form has to be tailored to the particular case
considered. For example the matrix
Arepresents connections and the structure of this
matrix
A(triangular, Hessenberg, sparse ...) depends on the
disease.