We have investigated kinetic models for bacterial
chemotaxis following Alt and co-authors, Erban and Othmer,
Dolak and Schmeiser. First we have analysed the possible
mathematical behaviours of such models. We have shown that
a critical mass phenomenon occurs in dimension
N= 2as for the classical
Keller-Segel model (with N. Bournaveas, Univ. Edimburgh).
This is one of the few existing results concerning blow-up
in kinetic models. The hyperbolic limit of this toy model
is under investigation.
Second, we have developped a quantitative approach based on a couple of experiments performed by J. Saragosti in the team of A. Buguin and P. Silberzan (Institut Curie, Paris). These experiments describe with full statistical details solitary waves of bacteria E. coli in narrow channels. On the first set of experiments we have demonstrated that the drift-diffusion approximation of the kinetic model is valid and it fits the data very well (publication in PLoS Comput. Biol., Figure ). On the second set of experiments we have simulated the kinetic model to obtain the best results as compared to the data in this context (work recently submitted). We believe that the full kinetic model is required to describe the data.
This leads to a new class of chemotaxis models, which differ significantly from the classical Keller-Segel model because they lack a gradient structure in the attractive field. We have started a systematic analysis of these models. This is a work in progress with N. Bournaveas (Univ. Edimburgh), F. Chardard (ENS de Lyon) and Ch. Schmeiser (Univ. Vienna). This analysis includes existence of inhomogeneous steady states, stability, speed of relaxation towards equilibrium.
- Mathematical analysis of the Keller-Segel model
[In collaboration with J.A. Carrillo and J. Rosado (UAB, Barcelona)]
Following McCann 1997 and Otto 2001, we interpret the classical Keller-Segel system for chemotaxis as a gradient flow in the Wasserstein space. The free-energy functional turns out to be homogeneous. This viewpoint helps to understand better blow-up mechanisms, and to derive rates of convergence towards self-similar profiles. We investigate more precisely linear diffusion, porous medium diffusion and fast diffusion in competition with various interaction kernels.
[In collaboration with N. Meunier (Paris 5) and R. Voituriez (Paris 6)]
Another project consists in analyzing some variant of the Keller-Segel system when the chemoattractant is secreted at the boundary of the domain. This is motivated by modeling issues in cell polarization.
- Kinetic models for bacterial collective motion
[In collaboration with N. Bournaveas (Univ. Edinburgh)]
We shed a new light on the theoretical analysis of kinetic equations for chemotaxis: we exhibited a peculiar example subject to a critical mass phenomenon as for the two-dimensional Keller-Segel system. This shows a posteriori that previous attempts to show global existence were in fact borderline with respect to this critical example.
[In collaboration with N. Bournaveas (Univ. Edinburgh), B. Perthame (Paris 6), A. Buguin, Jonathan Saragosti and P. Silberzan (Institut Curie, Paris)]
We have developed a macroscopic model for bacterial traveling pulses based on a mesoscopic description of the run-and-tumble process. We are able to capture some key features observed in the experiments (asymmetric profile, speed of the pulse).
To investigate the growth of a tumor it is crucial to have a correct description of its mechanical aspects. Tumoral and normal cells may be seen as a complex fluid, with complex rheology.
Numerical investigations of complex flows is studied by P. Vigneaux who develops new numerical schemes for Bingham type flows (viscoplastic flows).
We have analysed thoroughly recent models describing spontaneous polarisation of cells (e.g. neuron growth cones or budding yeast). These models combine a diffusive term (in the cytoplasm) plus an advective field created at the membrane and diffusing in the cytoplasm (accounting for the actin network or the microtubules). This can be compared to the classical Keller-Segel model where diffusion competes with a non-local attractive field. Going beyond linear stability analysis we have used our know-how of the Keller-Segel system to derive global existence (no polarisation) and blow-up (possibly polarisation) criteria. We have also performed some numerical experiments to determine the models which exhibit spontaneous polarisation. We have confirmed the prediction made by the physicists claiming that the microtubules cannot drive the cell into spontaneous polarisation whereas the actin network can.
In her PhD thesis (defended in december 2010), S. Enault proved a serie of existence results for tumor growth models
Incompressible models
Let
cbe the density of tumoral cells and
sthe density of sane cells. Then as a first
modelling, we assume that
cand
vare transported by a velocity field
vderiving from a pressure
p, and of course that tumoral cells multiply. This
gives
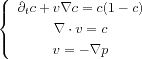
Following the arguments of Kato on 2D
incompressible Euler equations, S. Enault proves the
existence of global weak solutions in
Rd, for Lipschitz compact supported initial data. If
the initial condition is more regular, we get global
smooth solutions of this system.
Compressible models:
An other classical model is to consider that the tumor is incompressible whereas the sane cells are compressible. This leads to
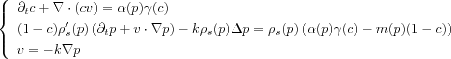
which is a delicate degenerated parabolic system. S. Enault proves the existence of a strong solution, in small time, in a bounded domain.
S. Enault also compares the two previous systems to investigate the effect of compressibility on the dynamics of the tumor.
In some cases it is natural to assume that sane and tumoral cells reacts with a different velocity to a gradient pressure, which leads to
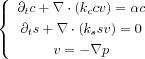
When
ks![]()
kcthen S. Enault proves that there exists smooth
initial data leading to the apparition of a discontinuity
(shock) in finite time. On the contrary when
ks=
kcthen for any smooth initial data there
exists a unique smooth global solution.