Scientific Foundations
General overview
There are two broad approaches for computational
specifications. In the
computation as modelapproach, computations are encoded
as mathematical structures containing nodes, transitions, and
state. Logic is used to
describethese structures, that is, the computations
are used as models for logical expressions. Intensional
operators, such as the modals of temporal and dynamic logics
or the triples of Hoare logic, are often employed to express
propositions about the change in state.
The
computation as deductionapproach, in contrast,
expresses computations logically, using formulas, terms,
types, and proofs as computational elements. Unlike the model
approach, general logical apparatus such as cut-elimination
or automated deduction becomes directly applicable as tools
for defining, analyzing, and animating computations. Indeed,
we can identify two main aspects of logical specifications
that have been very fruitful:
Proof normalization, which treats the state of a
computation as a proof term and computation as
normalization of the proof terms. General reduction
principles such as
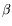 -reduction or cut-elimination are merely
particular forms of proof normalization. Functional
programming is based on normalization
-reduction or cut-elimination are merely
particular forms of proof normalization. Functional
programming is based on normalization
Proof search, which views the state of a
computation as a a structured collection of formulas,
known as a
sequent, and proof search in a suitable sequent
calculus as encoding the dynamics of the computation.
Logic programming is based on proof search
While the distinction between these two aspects is
somewhat informal, it helps to identify and classify
different concerns that arise in computational semantics. For
instance, confluence and termination of reductions are
crucial considerations for normalization, while unification
and strategies are important for search. A key challenge of
computational logic is to find means of uniting or
reorganizing these apparently disjoint concerns.
An important organizational principle is structural proof
theory, that is, the study of proofs as syntactic, algebraic
and combinatorial objects. Formal proofs often have
equivalences in their syntactic representations, leading to
an important research question about
canonicityin proofs – when are two proofs “essentially
the same?” The syntactic equivalences can be used ro derive
normal forms for proofs that illuminate not only the proofs
of a given formula, but also its entire proof search space.
The celebrated
focusingtheorem of Andreoli
Type theory is another important organizational principle,
but most popular type systems are generally designed for
either search or for normalization. To give some examples,
the Coq system
The Parsifal team investigates both the search and the
normalization aspects of computational specifications using
the concepts, results, and insights from proof theory and
type theory.
Focused proof systems
Focusing
A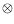 (
(
B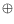
C), assuming
A,
Band
Care negative, is the ternary connective
-
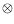 (-
(-
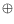 -)instead of the composition of two
binary connectives; in particular,
-)instead of the composition of two
binary connectives; in particular,
B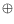
Cneed not even be considered as a subformula. Indeed,
focusing has proven to be crucial in controlling the search
behavior of automated theorem provers
Focusing is very important for logical specifications of
computations because synthetic inference rules have a direct
correspondence with computational steps. When a system is
encoded logically, we can identify at least three levels of
adequacyof the encoding:
Global adequacy, wherein the encoding does not
necessarily respect the structure of the computation, but
where soundness is ensured globally. For instance, an
encoding of one proof system in another is globally
adequate if it preserves truth and provability.
Full adequacy, where the structure of the entire
computation is preserved. For encodings of proof systems,
full adequacy corresponds to a one-to-one correspondence
between full proofs in the source and the target of the
encoding.
Local adequacy, where the structure of individual
steps of a computation is preserved,
i.e., the encoding is a bi-simulation. An encoding
of a proof system is locally adequate if the encoding
preserves the individual inference rules of the proof
system.
Locally adequate encodings give the best indication of the
strength and generality of proof systems, but in all but the
most trivial cases such encodings only exist if the target of
the encoding is a focused proof system. The members of the
Parsifal team have identified and proved a number of adequacy
results in recent years
Focusing is therefore an important tool in the study of
universalityof proof systems. We already know that
linear logic can serve as a uniform meta-language for a
number of proof systems, both classical and intuitionistic,
but these encoded systems generally are not able to
communicate with each other. Liang and Miller have been
building proof systems for combinations of classical,
intuitionistic, and linear logics that allows proofs in these
different systems to communicate via carefully chosen
cuts.
Reasoning about logic specifications
A long term project of members of the Parsifal team has
been the design of a powerful logic to reason about
computational specifications written in logic. Coming up with
the design of a logic that allows reasoning richly over
relational specifications involving bindings in syntax has
been a long standing problem, dating from at least the early
papers by McDowell and Miller
 gained enough expressive power to allow for natural
and declarative descriptions of invariants over logic-based
context.
gained enough expressive power to allow for natural
and declarative descriptions of invariants over logic-based
context.
The presence of nominal abstraction in
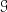 makes it possible for that logic to express predicates
that strongly resemble those found in Pitt's “nominal logic”
makes it possible for that logic to express predicates
that strongly resemble those found in Pitt's “nominal logic”
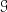 and nominal logic different in several ways, it is
possible to find an interesting subset of both logics that
do, in fact, correspond directly. In particular, Gacek showed
and nominal logic different in several ways, it is
possible to find an interesting subset of both logics that
do, in fact, correspond directly. In particular, Gacek showed
 Prolog
Prolog
 .
.
The
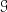 logic is the logic that is implemented by the Abella
prover of Andrew Gacek. This implementation has permitted a
large number of example theorems and proofs to be done
completely formally within
logic is the logic that is implemented by the Abella
prover of Andrew Gacek. This implementation has permitted a
large number of example theorems and proofs to be done
completely formally within
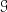 . As a result, we have gained a great deal of
confidence in the expressive strengths of his logic.
. As a result, we have gained a great deal of
confidence in the expressive strengths of his logic.
Deep inference and categorical
axiomatizations
Deep inference
One reason for using categories in proof theory is to give
a precise algebraic meaning to the identity of proofs: two
proofs are the same if and only if they give rise to the same
morphism in the category. Finding the right axioms for the
identity of proofs for classical propositional logic has for
long been thought to be impossible, due to “Joyal's Paradox”.
For the same reasons, it was believed for a long time that it
it not possible to have proof nets for classical logic.
Nonetheless, Lutz Strassburger and François Lamarche provided
proof nets for classical logic in
The following research problems are investigated by
members of the Parsifal team:
Find deep inference system for richer
logics. This is necessary for making the proof theoretic
results of deep inference accessible to applications as
they are described in the previous sections of this
report.
Investigate the possibility of
focusing proofs in deep inference. As described before,
focusing is a way to reduce the non-determinism in proof
search. However, it is well investigated only for the
sequent calculus. In order to apply deep inference in
proof search, we need to develop a theory of focusing for
deep inference.
Use the results on deep inference to
find new axiomatic description of categories of proofs
for various logics. So far, this is well understood only
for linear and intuitionistic logics. Already for
classical logic there is no common accepted notion of
proof category. How logics like LINC can be given a
categorical axiomatisation is completely open.
Proof nets and atomic flows
Proof nets and atomic flows are abstract (graph-like)
presentations of proofs such that all "trivial rule
permutations" are quotiented away. Ideally the notion of
proof net should be independent from any syntactic formalism.
But due to the almost absolute monopoly of the sequent
calculus, most notions of proof nets proposed in the past
were formulated in terms of their relation to the sequent
calculus. Consequently we could observe features like “boxes”
and explicit “contraction links”. The latter appeared not
only in Girard's proof nets
The concept of deep inference allows to design entirely
new kinds of proof nets. The work by Lamarche and
Strassburger
Extend the work of Lamarche and
Strassburger to larger fragments of linear logic,
containing the additives, the exponentials, and the
quantifiers, as started in
Finding (for classical logic) a notion
of proof nets that is deductive, i.e., can effectively be
used for doing proof search. An important property of
deductive proof nets must be that the correctness can be
checked in linear time. For the classical logic proof
nets by Lamarche and Strassburger
Studying the normalization of proofs
in classical logic using atomic flows. Although there is
no correctness criterion they allow to simplify the
normalization procedure for proofs in deep inference, and
additionally allow to get new insights in the complexity
of the normalization.
A systematic approach to
cut-elimination
One of the main problems of proof theory is to prove cut
elimination for new logics. Usually, a cut elimination proof
is a tedious case analysis, and, in general, it is very
fragile and not modular
It is therefore an important research task, to find a more
systematic approach to cut elimination proofs. That is to
say, to find general guidelines that ensure the cut
elimination property for large classes of systems, in a
similar way as it has been done for display logics
Proof search in type theory
Cross-fertilizing ideas between the proof search approach
and the proof normalization approach, Lengrand has interacted
with the TypiCal (INRIA Saclay) and the

r2(INRIA Rocquencourt) project-teams.
In proof assistants based on the proof normalization
approach, or Type Theory, it is a hard challenge to design
and understand their proof search mechanisms. Based on ideas
from
By doing so, we have helped improve the Coq system, by
impacting the design of the new version of the tool's proof
engine. One of these proof search mechanisms, known as
pattern unification, has again become a hot topic of
Coq's design, after Lengrand's use of Coq to specify a
particular algorithm has revealed a drastic need for this
missing feature.
It also emerged from Lengrand's interaction with these
project-teams, that bridging Type Theory with the proof
theory developed at Parsifal confirms the need for more
extensionality on the functions programmed in Coq. Efforts to
add such extensionality are ongoing.
Application Domains
Automated theorem proving
Automated theorem proving has traditionally focused on
classical first-order logic, but non-classical logics are
increasingly becoming important in the specification and
analysis of software. Most type systems are based on
(possibly second-order) propositional intuitionistic logic,
for example, while resource-sensitive and concurrent systems
are most naturally expressed in linear logic.
The members of the Parsifal team have a strong expertise
in the design and implementation of performant automated
reasoning systems for such non-classical logics. In
particular, the Linprover suite of provers
Any non-trivial specification, of course, will involve
theorems that are simply too complicated to prove
automatically. It is therefore important to design
semi-automated systems that allow the user to give high level
guidance, while at the same time not having to write every
detail of the formal proofs. High level proof languages in
fact serve a dual function – they are more readily
comprehended by human readers, and they tend to be more
robust with respect to maintenance and continued evolution of
the systems. Members of the Parsifal team, in association
with other INRIA teams and Microsoft Research, have been
building a heterogeneous semi-automatic proof system for
verifying distributed algorithms (see Section.
On a more foundational level, the team has been developing
many new insights into the structure of proofs and the proof
searh spaces. Two directions, in particular, present
tantalizing possibilities:
The concept of
multi-focusing
The use of
bounded search, where the bounds can be shown to
be complete by meta-theoretic analysis, can be used to
circumvent much of the non-determinism inherent in
resource-sensitive logics such as linear logic. The lack
of proofs of a certain bound can then be used to justify
the presence or absence of properties of the encoded
computations.
Much of the theoretical work on automated reasoning has
been motivated by examples and implementations, and the
Parsifal team intends to continue to devote significant
effort in these directions.
Mechanized metatheory
There has been increasing interest in the use of formal
methods to provide proofs of properties of programs and
programming languages. Tony Hoare's Grand Challenge titled
“Verified Software: Theories, Tools, Experiments” has as a
goal the construction of “verifying compilers” for a world
where programs would only be produced with machine-verified
guarantees of adherence to specified behavior. Guarantees
could be given in a number of ways: proof certificates being
one possibility.
The POPLMark challenge
The Parsifal team has developed several tools and
techniques for reasoning about the meta-theory of programming
languages. One of the most important requirements for
progamming languages is the ability to reason about data
structures with binding constructs upto
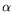 -equivalence. The use of higher-order syntax and
nominal techniques for such data structures was pioneered by
Miller, Nadathur and Tiu. The Abella system (see
Section.
-equivalence. The use of higher-order syntax and
nominal techniques for such data structures was pioneered by
Miller, Nadathur and Tiu. The Abella system (see
Section.
 -calculus.
-calculus.
Another important feature for the meta-theory of
progamming languages is the ability to reason about inductive
and co-inductive data structures and algorithms. While
systems such as Coq
Modern programming languages are increasingly
incorporating distributed, concurrent, reactive, and
real-time elements. In such languages, it is often necessary
to reason not about executions but about
behaviors, that is, it is necessary to compare the
behavior of two different programs instead of characterizing
all executions of a single program. The Bedwyr tool
 -calculus processes. It is a prototype of the kind of
formal tools that will be necessary for the programming
languages of the future.
-calculus processes. It is a prototype of the kind of
formal tools that will be necessary for the programming
languages of the future.
Malleable proof languages
One of the benefits of focused proof systems (see Section.
Recently, members of the Parsifal team have shown how to
specify a large variety of proof systems—including natural
deduction, the sequent calculus, and various tableau and free
deduction systems—uniformly using either focused linear
logic
It seems clear that a suitably general focused proof
system can serve as a universal proof language for a large
variety of proof systems. We can identify at least the
following major challenges:
Can focused proof systems serve as a
framework for broad spectrum proof certificates for such
domains as proof-carrying code or proof-carrying
authorization?
Can one design a proof language based
on focused proofs that allows for a variable amount of
verbosity in terms of a tunable trade off between
simplicity of the proof checker (or, equivalently, the
amount of search that the proof checker is allowed to
perform) and the size of proof certificates?
Can one design a generic universal
proof checker for a large variety of proof systems?
How does (co)induction in a focused
proof system compare to type systems such as Deduction
Modulo
Software
Abella
Andrew
Gacek
Dale
Miller
The earliest versions of the Abella theorem prover was
written while Gacek was a PhD student at the University of
Minnesota. During Gacek's post doc in the Parsifal team, he
and Miller have designed and implemented more features into
this prover. One such feature involves simplifying
dependences among variables. More explicitly, for Abella to
correctly capture the relationship between “meta-variables”
and binding, the prover takes several
raisingsteps that are responsible for explicitly
accounting for the dependence between these two kinds of
variables. Given the typing discipline of Abella it is
possible to statically determine that certain possible
dependences are, in fact, vacuous. Abella is now able to
remove these vacuous dependences: such a simplification makes
it possible to make simplify many Abella proofs. Gacek,
Miller, and Nadathur have also published two papers
describing the underlying theory of Abella.
For more information, see the
[Abella home page].
Tac
David
Baelde
Dale
Miller
Zachary
Snow
Alexandre
Viel
Given the team's expertise with the structure of proofs
and techniques for automation, we have taken on the
implementation of the TAC prover. This prover, written in
OCaml, has been used to prove a range of inductive theorems
in a completely automatic fashion. The architecture, which is
the subject of the conference paper
For more information, see the
[Tac home page].
TLAPS
Kaustuv
Chaudhuri
Denis
Cousineau
INRIA-MSR
Damien
Doligez
INRIA Paris-Rocquencourt, EPI
Gallium
Leslie
Lamport
Microsoft Research Silicon Valley
Stephan
Merz
INRIA Nancy Grand-Est, EPI Veridis
Hernán
Vanzetto
Masters Student, Université Henri Poincaré,
Nancy
The TLA
+Proof System (TLAPS)
The TLAPS is based on translation of a high level proof
language into proof obligations for various backend reasoning
systems, which include both off the shelf automated reasoning
systems (theorem provers, SMT solvers, etc.) and systems that
have been particularly engineered for the TLA language. The
backend systems may produce proofs that are then formally
checked in Isabelle/TLA
+, an axiomatization of TLA in the
Isabelle proof system. Some backend systems, such as decision
procedures for arithmetic, do not currently produce
proofs.
Also in 2010, the TLAPS was integrated into the TLA
Toolbox, an integrated development environment (IDE) for many
TLA-related tools, including the TLC model checker. The next
public release will include support for reasoning about
liveness, which will involve implementing a new temporal
reasoning framework.
For more information, see the
[TLAPS home page].
New Results
Proof normalization via atomic flows
Tom
Gundersen
Lutz
Strassburger
In a joint work with Alessio Guglielmi (University of
Bath), Tom Gundersen and Lutz Strassburger have given a novel
method for normalizing proofs in classical logic, which is
based on atomic flows. These are purely graphical devices
that abstract away from much of the typical bureaucracy of
proofs. We make crucial use of the
path breaker, an atomic-flow construction that avoids
some unpleasant termination problems, and that can be used in
any proof system with sufficient symmetry. We also give an
original 2-dimensional-diagram exposition of atomic flows,
which helps us to connect atomic flows with other known
formalisms. This work has been published in LICS 2010
Typing lambda-terms with deep
inference
Nicolas
Guenot
Lutz
Strassburger
Nicolas Guenot and Lutz Strassburger have been working on
extending the Curry-Howard correspondence to the notion of
deep inference. The result is a deductive system for
intuitionistic logic within deep inference, together with a
cut elimination procedure on one side, and a term calculus on
the other side. The terms are a variation of lambda terms,
and the normalization can simulate beta-reduction, and the
rewrite rules are in one-to-one correspondence to cut
elimination reduction rules in the deductive system.
Subexponential logic
Kaustuv
Chaudhuri
Dale
Miller
Subexponential logics are a family of refinements of
classical logic that are each parameterized by a collection
of
subexponentialconnectives arranged in a (pre)order.
Although the concept is quite old, Miller and Nigam have
shown in 2009 that focused derivations in subexponential
logics can adequately capture computations in a programming
language consisting of loops, iteration, and loads and stores
in
locations. More generally, Miller has argued that
subexponential logics have the potential to be the building
blocks of future specification languages for logical and
computational systems
Chaudhuri has shown that the classical and intuitionistic
dialects of polarized subexponential logics have the same
expressive power, in the sense that partial derivations of
sequents in one dialect are in one-to-one correspondence with
the partial derivations of the encoding of the sequents in
the other dialect. This result generalizes several known
adequacy theorems between particular subexponential logics,
and gives a new adequacy result for encodings of
intuitionistic logic in classical linear logic. This result
was published in CSL 2010
Dynamic polarity assignment
Kaustuv
Chaudhuri
It is well known that the
polarityof the atomic propositions in linear logic is
ambiguous – each atom may be
assigneda polarity arbitrarily without destroying the
completeness of focused derivations. If the atoms are
assigned their polarity statically, that is, before proof
search, then it is possible to obtain either forward chaining
(also known as program-directed reasoning) or backward
chaining (also known as goal-directed reasoning) semantics
for logic programs based on the chosen assignments. However,
it is not apparently possible to get the intersection of
these two strategies with purely static assignments.
Chaudhuri has shown that delaying the assignment of atomic
polarities until the proof search context can justify a
particular assignment can produce such a combined strategy.
This dynamic assignment strategy enjoys all the benefits of
forward chaining (locality, sharing, concurrency), but
terminates and gives the same set of answers as backward
chaining on terminating programs. Indeed, we obtain the same
semantics as the so-called
magic sets transformationof logic programs that is
based on rewriting the original program and queries, but,
since polarity assignment only constrains the proofs and does
not alter the programs, we avoid the non-compositional
overhead of program transformation. This work was published
in LPAR 2010
Heterogeneous verification for distributed
algorithms
Kaustuv
Chaudhuri
Damien
Doligez
INRIA Paris-Rocquencourt, EPI
Gallium
Leslie
Lamport
Microsoft Research Silicon Valley
Stephan
Merz
INRIA Nancy Grand-Est, EPI Veridis
The TLA
+Proof System (TLAPS), developed at
the INRIA-MSR joint centre in association with a number of
other INRIA teams, was released publicly. Chaudhuri designed
and implemented the
proof managercomponent of the tool that interprets
high level TLA
+proofs and delegates sub-problems
to various backend verifiers. The TLAPS was described in a
paper published in IJCAR 2010
[IFM 2010].
One of the goals of this project was to give fully
formalized correctness proofs of well known distributed
algorithms such as Lamport's Bakery Algorithm for distributed
mutual exclusion and the Paxos algorithm for distributed
consensus. In 2009, the safety part of the correctness of the
Bakery algorithm was successfully proved; this proof,
initially several thousands of lines long, has been used as a
benchmark for further development of the TLAPS and has now
shrunk to less than 100 lines after improvements to backend
reasoning; in the near future, we will be able to eliminate
essentially the entire proof by using a new SMT backend, now
in development.
In 2010, significant progress has also been made in
proving a number of Paxos algorithms correct, including a
novel unpublished version of Paxos that is Byzantine fault
tolerant.
Complexity of
 -terms and intersection types
Stéphane
Lengrand
Alexis
Bernadet
-terms and intersection types
Stéphane
Lengrand
Alexis
Bernadet
New complexity results have emerged from the study, in the
framework of non-idempotent type systems, of how
lambda-calculi manage resources.
It is well-known that strongly normalising terms of the
 -calculus can be characterized by a type system using
intersections. A term is of type
-calculus can be characterized by a type system using
intersections. A term is of type
A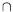
Bif it is both of type
Aand type
B.
Intersections are usually considered idempotent in that
A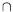
A=
A. But recent studies have
suggested that dropping this property would enrich types with
quantitative information.
The first result is a refinement, with quantitative
information, of the characterisation of strongly normalising
terms : the relevant complexity measure here
 -terms is the worst-case complexity (the length of
longest reduction sequences). This quantitative information
can now be read directly from typing trees. This result is
accepted for publication at the FOSSACS'2011 conference
-terms is the worst-case complexity (the length of
longest reduction sequences). This quantitative information
can now be read directly from typing trees. This result is
accepted for publication at the FOSSACS'2011 conference
This unveiled a tight connection between non-idempotent
intersections and the way data are erased and duplicated in
 -calculus, suggesting a move to the framework with
explicit substitutions. These allow a finer-grained control
of erasure and duplication in
-calculus, suggesting a move to the framework with
explicit substitutions. These allow a finer-grained control
of erasure and duplication in
 -calculus. The second result is a lift of the first
one to the explicit substitution framework, where our
analysis of resource management becomes finer-grained and
more interesting.
-calculus. The second result is a lift of the first
one to the explicit substitution framework, where our
analysis of resource management becomes finer-grained and
more interesting.
The third result is a new set of semantical tools for
 -calculi, based on filters and orthogonality
techniques. These tools simplify previously known proofs of
strong normalisation for traditional typing systems like
System F.
-calculi, based on filters and orthogonality
techniques. These tools simplify previously known proofs of
strong normalisation for traditional typing systems like
System F.
 -terms typable in System F are strongly normalising
and therefore typable with intersection types. In other
words, the infinite polymorphism given by System F is in
practice always reduced to the finite polymorphism given by
intersection types. Our tools explain how.
-terms typable in System F are strongly normalising
and therefore typable with intersection types. In other
words, the infinite polymorphism given by System F is in
practice always reduced to the finite polymorphism given by
intersection types. Our tools explain how.
A focused sequent calculus interacting with
decision procedures
Stéphane
Lengrand
Mahfuza
Farooque
Clément
Houtmann
This line of research pertains to the ANR-project PSI
(described below).
Inspired by techniques from SAT-modulo-theory, we have
designed a focused sequent calculus that can interact with
theory-specific decision procedures. Such a procedure is
assumed to be able to decide the consistency, with respect to
a particular theory, of conjunctions of atomic propositions
(with free variables) written in the theory's syntax.
Our sequent calculus organises an interplay between a
syntactic equality and a semantical / theory-based equality.
It is modular over the theories considered and the decision
procedures plugged-in.
We conjecture that the instance of our modular sequent
calculus with the procedure known as Congruence Closure is
sound and complete with respect to classical logic with
Leibniz's equality.
We have a candidate system for making this sequent
calculus suitable for proof-search using meta-variables and
syntactic unification, whose cohabitation with theories is
difficult (and is therefore absent from SAT-modulo-theory
solvers).
Towards a stochastic linear logic for biological
computation
Kaustuv
Chaudhuri
Joëlle
Despeyroux
In previous work, Joëlle Despeyroux and Kaustuv Chaudhuri
have given an encoding of the synchronous stochastic
 -calculus in a hybrid extension of intuitionistic
linear logic (called HyLL). Precisely, they have shown that
focused partial sequent derivations in the encoding are in
bijection with stochastic traces. The modal worlds are used
to represent the rates of stochastic interactions, and the
connectives of hybrid logic are used to represent the
constraints in the stochastic transition rules. These results
were presented in an extended report, available from
HAL
-calculus in a hybrid extension of intuitionistic
linear logic (called HyLL). Precisely, they have shown that
focused partial sequent derivations in the encoding are in
bijection with stochastic traces. The modal worlds are used
to represent the rates of stochastic interactions, and the
connectives of hybrid logic are used to represent the
constraints in the stochastic transition rules. These results
were presented in an extended report, available from
HAL
One of the most successful applications of the stochastic
 -calculus has been in representing signal transduction
networks in cellular biology. An interesting application of
this work would therefore be the direct representations of
biological processes in HyLL, the original motivation for
this line of investigation. Furthermore, other stochastic
systems can, at least in principle, be similarly encoded in
HyLL, giving us the linguistic ability to compare and combine
systems represented using different stochastic
formalisms.
-calculus has been in representing signal transduction
networks in cellular biology. An interesting application of
this work would therefore be the direct representations of
biological processes in HyLL, the original motivation for
this line of investigation. Furthermore, other stochastic
systems can, at least in principle, be similarly encoded in
HyLL, giving us the linguistic ability to compare and combine
systems represented using different stochastic
formalisms.
This year, a new definition of the stochastic constraints
part of the logic was given. While the new definition is more
general than the previous one, it is still not yet
satisfactory; More work is needed to provide hyll with the
expressiveness of the traditional temporal logic used to
reason on biological computations.
![]() -calculus
-calculus![]() -calculus, game semantics,
etc.
-calculus, game semantics,
etc.