For polynomial system solving, the mathematical specification of the result of a computation, in particular when the number of solutions is infinite, is itself a difficult problem , , . Sorting the most frequently asked questions appearing in the applications, one distinguishes several classes of problems which are different either by their mathematical structure or by the significance that one can give to the word "solving".
Some of the following questions have a different meaning in the real case or in the complex case, others are posed only in the real case :
zero-dimensional systems (with a finite number of complex solutions - which include the particular case of univariate polynomials); The questions in general are well defined (numerical approximation, number of solutions, etc) and the handled mathematical objects are relatively simple and well-known;
parametric systems; They are generally zero-dimensional for almost all the parameters' values. The goal is to characterize the solutions of the system (number of real solutions, existence of a parameterization, etc.) with respect to parameters' values.
positive dimensional systems; For a direct application, the first question is the existence of zeros of a particular type (for example real, real positive, in a finite field). The resolution of such systems can be considered as a black box for the study of more general problems (semi-algebraic sets for example) and information to be extracted is generally the computation of a point per connected component in the real case.
constructible and semi-algebraic sets; As opposed to what occurs numerically, the addition of constraints or inequalities complicates the problem. Even if semi-algebraic sets represent the basic object of the real geometry, their automatic "and effective study" remains a major challenge. To date, the state of the art is poor since only two classes of methods are existing :
the Cylindrical Algebraic Decomposition which basically computes a partition of the ambient space in cells where the signs of a given set of polynomials are constant;
deformations based methods that turn the problem into solving algebraic varieties.
The first solution is limited in terms of performances (maximum 3 or 4 variables) because of a recursive treatment variable by variable, the second also because of the use of a sophisticated arithmetic (formal infinitesimals).
quantified formulas; deciding efficiently if a first order formula is valid or not is certainly one of the greatest challenges in "effective" real algebraic geometry. However this problem is relatively well encircled since it can always be rewritten as the conjunction of (supposed to be) simpler problems like the computation of a point per connected component of a semi-algebraic set.
As explained in some parts of this document, the iniquity of the studied mathematical objects does not imply the uncut of the related algorithms. The priorities we put on our algorithmic work are generally dictated by the applications. Thus, above items naturally structure the algorithmic part of our research topics.
For each of these goals, our work is to design the most efficient possible algorithms: there is thus a strong correlation between implementations and applications, but a significant part of the work is dedicated to the identification of black-box allowing a modular approach of the problems. For example, the resolution of the zero-dimensional systems is a prerequisite for the algorithms treating of parametric or positive dimensional systems.
An essential class of black-box developed in the project does not appear directly in the absolute objectives counted above : the "algebraic or complex" resolutions. They are mostly reformulations, more algorithmically usable, of the studied systems. One distinguishes two categories of complementary objects :
ideals representations; From a computational point of view these are the structures which are used in the first steps;
varieties representations; The algebraic variety, or more generally the constructible or semi-algebraic set is the studied object.
To give a simple example, in
![]() the variety
{(0, 0)}can be seen like the zeros
set of more or less complicated ideals (for example, ideal(
the variety
{(0, 0)}can be seen like the zeros
set of more or less complicated ideals (for example, ideal(
X,
Y), ideal(
X2,
Y), ideal(
X2,
X,
Y,
Y3), etc). The entry which is given to us is
a system of equations, i.e. an ideal. It is
essential, in many cases, to understand the structure of this
object to be able to correctly treat the degenerated cases. A
striking example is certainly the study of the singularities.
To take again the preceding example, the variety is not
singular, but this cannot be detected by the blind
application of the Jacobian criterion (one could wrongfully
think that all the points are singular, contradicting, for
example, Sard's lemma).
The basic tools that we develop and use to understand in an automatic way the algebraic and geometrical structures are on the one hand Gröbner bases (the most known object used to represent an ideal without loss of information) and on the other hand triangular sets (effective way to represent the varieties).
Let us denote by
K[
X1, ...,
Xn]the ring of polynomials with coefficients in a
field
Kand indeterminates
X1, ...,
Xnand
S= {
P1, ...,
Ps}any subset of
K[
X1, ...,
Xn]. A point
![]() is a zero of
is a zero of
Sif
Pi(
x) = 0
i![]() [1...
[1...
s].
The ideal
![]() generated by
generated by
P1, ...,
Psis the set of polynomials in
K[
X1, ...,
Xn]constituted by all the combinations
![]() with
with
![]() . Since every element of
. Since every element of
![]() vanishes at each zero of
vanishes at each zero of
S, we denote by
![]() (resp.
(resp.
![]() ), the set of complex (resp. real) zeros of
), the set of complex (resp. real) zeros of
S, where
Ris a real closed field containing
Kand
Cits algebraic closure.
One Gröbner basis' main property is to provide an
algorithmic method for deciding if a polynomial belongs or
not to an ideal through a reduction function denoted "
![]() " from now.
" from now.
If
Gis a Gröbner basis of an ideal
![]() for any monomial ordering
<.
for any monomial ordering
<.
a polynomial
![]() belongs to
belongs to
![]() if and only if
if and only if
![]() ,
,
Reduce(
p,
G,
<) does not depend on the
order of the polynomials in the list
G, thus, this is a canonical reduced expression
modulus
![]() , and the Reduce function can be used as a
simplificationfunction.
, and the Reduce function can be used as a
simplificationfunction.
Gröbner bases are computable objects. The most popular method for computing them is Buchberger's algorithm ( , ). It has several variants and it is implemented in most of general computer algebra systems like Maple or Mathematica. The computation of Gröbner bases using Buchberger's original strategies has to face to two kind of problems :
(A) arbitrary choices : the order in which are done the computations has a dramatic influence on the computation time;
(B) useless computations : the original algorithm spends most of its time in computing 0.
For problem (A), J.C. Faugère proposed (
- algorithm
F4) a new generation of powerful algorithms (
) based on the intensive use of
linear algebra technics. In short, the arbitrary choices are
left to computational strategies related to classical linear
algebra problems (matrix inversions, linear systems,
etc.).
For problem (B), J.C. Faugère proposed ( ) a new criterion for detecting useless computations. Under some regularity conditions on the system, it is now proved that the algorithm do never perform useless computations.
A new algorithm named
F5was built using these two key results. Even if it
still computes a Gröbner basis, the gap with existing other
strategies is consequent. In particular, due to the range of
examples that become computable, Gröbner basis can be
considered as a reasonable computable object in large
applications.
We pay a particular attention to Gröbner bases computed for elimination orderings since they provide a way of "simplifying" the system (equivalent system with a structured shape). A well known property is that the zeros of the first non null polynomial define the Zariski closure (classical closure in the case of complex coefficients) of the projection on the coordinate's space associated with the smallest variables.
Such kinds of systems are algorithmically easy to use, for computing numerical approximations of the solutions in the zero-dimensional case or for the study of the singularities of the associated variety (triangular minors in the Jacobian matrices).
Triangular sets have a simplier structure, but, except if they are linear, algebraic systems cannot, in general, be rewritten as a single triangular set, one speaks then of decomposition of the systems in several triangular sets.
| Lexicographic Gröbner bases | Triangular sets |
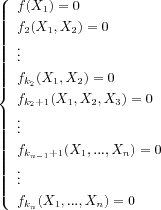
|
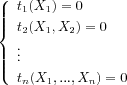
|
Triangular sets appear under various names in the field of algebraic systems. J.F. Ritt ( ) introduced them as characteristic sets for prime ideals in differential algebra. His constructive algebraic tools were adapted by W.T. Wu in the late seventies for geometric applications. The concept of regular chain (see and ) is adapted for recursive computations in a univariate way.
It provides a membership test and a zero-divisor test for
the strongly unmixed dimensional ideal it defines.
Kalkbrenner defined regular triangular sets and showed how to
decompose algebraic varieties as a union of Zariski closures
of zeros of regular triangular sets. Gallo showed that the
principal component of a triangular decomposition can be
computed in
O(
dO(
n2))(
n= number of variables,
d=degree in the variables). During the 90s,
implementations of various strategies of decompositions
multiply, but they drain relatively heterogeneous
specifications.
D. Lazard contributed to the homogenization of the work completed in this field by proposing a series of specifications and definitions gathering the whole of former work . Two essential concepts for the use of these sets (regularity, separability) at the same time allow from now on to establish a simple link with the studied varieties and to specify the computed objects precisely.
A remarkable and fundamental property in the use we have of the triangular sets is that the ideals induced by regular and separable triangular sets, are radical and equidimensional. These properties are essential for some of our algorithms. For example, having radical and equidimensional ideals allows us to compute straightforwardly the singular locus of a variety by canceling minors of good dimension in the Jacobian matrix of the system. This is naturally a basic tool for some algorithms in real algebraic geometry , , .
In 1993, Wang proposed a method for decomposing any polynomial system into finetriangular systems which have additional properties such as the projection property that may be used for solving parametric systems (see Section ).
Triangular sets based techniques are efficient for specific problems, but the implementations of direct decompositions into triangular sets do not currently reach the level of efficiency of Gröbner bases in terms of computable classes of examples. Anyway, our team benefits from the progress carried out in this last field since we currently perform decompositions into regular and separable triangular sets through lexicographical Gröbner bases computations.
A system is zero-dimensional if the set of the solutions in an algebraically closed field is finite. In this case, the set of solutions does not depend on the chosen algebraically closed field.
Such a situation can easily be detected on a Gröbner basis for any admissible monomial ordering.
These systems are mathematically particular since one can
systematically bring them back to linear algebra problems.
More precisely, the algebra
K[
X1, ...,
Xn]/
Iis in fact a
K-vector space of dimension equal to the number of
complex roots of the system (counted with multiplicities). We
chose to exploit this structure. Accordingly, computing a
base of
K[
X1, ...,
Xn]/
Iis essential. A Gröbner basis
gives a canonical projection from
K[
X1, ...,
Xn]to
K[
X1, ...,
Xn]/
I, and thus provides a base of the
quotient algebra and many other informations more or less
straightforwardly (number of complex roots for example).
The use of this vector-space structure is well known and at the origin of the one of the most known algorithms of the field ( ) : it allows to deduce, starting from a Gröbner basis for any ordering, a Gröbner base for any other ordering (in practice, a lexicographic basis, which are very difficult to compute directly). It is also common to certain semi-numerical methods since it allows to obtain quite simply (by a computation of eigenvalues for example) the numerical approximation of the solutions (this type of algorithms is developed, for example, in the INRIA Galaad project).
Contrary to what is written in a certain literature, the computation of Gröbner bases is not "doubly exponential" for all the classes of problems. In the case of the zero-dimensional systems, it is even shown that it is simply exponential in the number of variables, for a degree ordering and for the systems without zeros at infinity. Thus, an effective strategy consists in computing a Gröbner basis for a favorable ordering and then to deduce, by linear algebra technics, a Gröbner base for a lexicographic ordering .
The case of the zero-dimensional systems is also specific for triangular sets. Indeed, in this particular case, we have designed algorithms that allow to compute them efficiently starting from a lexicographic Gröbner basis. Note that, in the case of zero-dimensional systems, regular triangular sets are Gröbner bases for a lexicographical order.
Many teams work on Gröbner bases and some use triangular sets in the case of the zero-dimensional systems, but up to our knowledge, very few continue the work until a numerical resolution and even less tackle the specific problem of computing the real roots. It is illusory, in practice, to hope to obtain numerically and in a reliable way a numerical approximation of the solutions straightforwardly from a lexicographical basis and even from a triangular set. This is mainly due to the size of the coefficients in the result (rational number).
Our specificity is to carry out the computations until their term thanks to two types of results :
the computation of the Rational
Univariate Representation
: we proved that any
zero-dimensional system, depending on variables
X1, ...
Xn, can systematically be rewritten, without
loss of information (multiplicities, real roots), in the
form
f(
T) = 0,
Xi=
gi(
T)/
g(
T),
i= 1...
nwhere the polynomials
f,
g,
g1, ...
gnhave coefficients in the same ground field
as those of the system and where
Tis a new variable (independent from
X1, ...
Xn).
efficient algorithms for isolating and counting the real roots of univariate polynomials .
Thus, the use of innovative algorithms for Gröbner bases computations , , Rational Univariate representations ( for the "shape position" case and for the general case), allows to use zero-dimensional solving as sub-task in other algorithms.
When a system is positive dimensional(with an infinite number of complex roots), it is no more possible to enumerate the solutions. Therefore, the solving process reduces to decomposing the set of the solutions into subsets which have a well-defined geometry. One may perform such a decomposition from an algebraic point of view or from a geometrical one, the latter meaning not taking the multiplicities into account (structure of primary components of the ideal is lost).
Although there exist algorithms for both approaches, the algebraic point of view is presently out of the possibilities of practical computations, and we restrict ourselves to geometrical decompositions.
When one studies the solutions in an algebraically closed field, the decompositions which are useful are the equidimensional decomposition (which consists in considering separately the isolated solutions, the curves, the surfaces, ...) and the prime decomposition (decomposes the variety into irreducible components). In practice, our team works on algorithms for decomposing the system into regular separable triangular sets, which corresponds to a decomposition into equidimensional but not necessarily irreducible components. These irreducible components may be obtained eventually by using polynomial factorization.
However, in many situations one is looking only for real
solutions satisfying some inequalities (
Pi>0or
Pi![]() 0)
0)
There are general algorithms for such tasks, which rely on Tarski's quantifier elimination. Unfortunately, these problems have a very high complexity, usually doubly exponential in the number of variables or the number of blocks of quantifiers, and these general algorithms are intractable. It follows that the output of a solver should be restricted to a partial description of the topology or of the geometry of the set of solutions, and our research consists in looking for more specific problems, which are interesting for the applications, and which may be solved with a reasonable complexity.
We focus on 2 main problems:
1. computing one point on each connected components of a semi-algebraic set;
2. solving systems of equalities and inequalities depending on parameters.
The most widespread algorithm computing sampling points in a semi-algebraic set is the Cylindrical Algebraic Decomposition Algorithm due to Collins . With slight modifications, this algorithm also solves the problem of Quantifier Elimination. It is based on the recursive elimination of variables one after an other ensuring nice properties between the components of the studied semi-algebraic set and the components of semi-algebraic sets defined by polynomial families obtained by the elimination of variables. It is doubly exponential in the number of variables and its best implementations are limited to problems in 3 or 4 variables.
Since the end of the eighties, alternative strategies (see , and references therein) with a single exponential complexity in the number of variables have been developed. They are based on the progressive construction of the following subroutines:
(a) solving zero-dimensional systems: this can be performed by computing a Rational Univariate Representation (see );
(b) computing sampling points in a real hypersurface: after some infinitesimal deformations, this is reduced to problem (a) by computing the critical locus of a polynomial mapping reaching its extrema on each connected component of the real hypersurface;
(c) computing sampling points in a real algebraic variety defined by a polynomial system: this is reduced to problem (b) by considering the sum of squares of the polynomials;
(d) computing sampling points in a semi-algebraic set: this is reduced to problem (c) by applying an infinitesimal deformation.
On the one hand, the relevance of this approach is based on the fact that its complexity is asymptotically optimal. On the other hand, some important algorithmic developments have been necessary to obtain efficient implementations of subroutines (b) and (c).
During the last years, we focused on providing efficient algorithms solving the problems (b) and (c). The used method rely on finding a polynomial mapping reaching its extrema on each connected component of the studied variety such that its critical locus is zero-dimensional. For example, in the case of a smooth hypersurface whose real counterpart is compact choosing a projection on a line is sufficient. This method is called in the sequel the critical point method. We started by studying problem (b) . Even if we showed that our solution may solve new classes of problems ( ), we have chosen to skip the reduction to problem (b), which is now considered as a particular case of problem (c), in order to avoid an artificial growth of degree and the introduction of singularities and infinitesimals.
Putting the critical point method into practice in the general case requires to drop some hypotheses. First, the compactness assumption, which is in fact intimately related to an implicit properness assumption, has to be dropped. Second, algebraic characterizations of critical loci are based on assumptions of non-degeneracy on the rank of the Jacobian matrix associated to the studied polynomial system. These hypotheses are not satisfied as soon as this system defines a non-radical ideal and/or a non equidimensional variety, and/or a non-smooth variety. Our contributions consist in overcoming efficiently these obstacles and several strategies have been developed , .
The properness assumption can be dropped by considering the square of a distance function to a generic point instead of a projection function: indeed each connected component contains at least a point minimizing locally this function. Performing a radical and equidimensional decomposition of the ideal generated by the studied polynomial system allows to avoid some degeneracies of its associated Jacobian matrix. At last, the recursive study of overlapped singular loci allows to deal with the case of non-smooth varieties. These algorithmic issues allow to obtain a first algorithm with reasonable practical performances.
Since projection functions are linear while the distance function is quadratic, computing their critical points is easier. Thus, we have also investigated their use. A first approach consists in studying recursively the critical locus of projection functions on overlapped affine subspaces containing coordinate axes combined with the study of their set of non-properness. A more efficient one , avoiding the study of sets of non-properness is obtained by considering iteratively projections on genericaffine subspaces restricted to the studied variety and fibers on arbitrary points of these subspaces intersected with the critical locus of the corresponding projection. The underlying algorithm is the most efficient we obtained.
In terms of complexity, we have proved in that when the studied polynomial system generates a radical ideal and defines a smooth algebraic variety, the output of our algorithms is smaller than what could be expected by applying the classical Bèzout bound and than the output of the previous algorithms. This has also given new upper bounds on the number of connected components of a smooth real algebraic variety which improve the classical Thom-Milnor bound. The technique we used, also allows to prove that the degree of the critical locus of a projection function is inferior or equal to the degree of the critical locus of a distance function. Finally, it shows how to drop the assumption of equidimensionality required in the aforementioned algorithms.
Most of the applications we recently solved (celestial mechanics, cuspidal robots, statistics, etc.) require the study of semi-algebraic systems depending on parameters. Although we covered these subjects in an independent way, some general algorithms for the resolution of this type of systems can be proposed from these experiments.
The general philosophy consists in studying the generic solutions independently from algebraic subvarieties (which we call from now on discriminant varieties) of dimension lower than the semi-algebraic set considered. The study of the varieties thus excluded can be done separately to obtain a complete answer to the problem, or is simply neglected if one is interested only in the generic solutions, which is the case in some applications.
We recently proposed a new framework for studying basic constructible (resp. semi-algebraic) sets defined as systems of equations and inequations (resp. inequalities) depending on parameters. Let's consider the basic semi-algebraic set
![]()
and the basic constructible set
![]()
where
pi,
fjare polynomials with rational
coefficients.
[
U,
X] = [
U
1, ...
U
d,
X
d+ 1, ...
X
n]is the set of
indeterminatesor variables,
U= [
U1, ...
Ud]is the set of
parametersand
X= [
Xd+ 1, ...
Xn]the set of
unknowns;
![]() is the set of polynomials defining the
equations;
is the set of polynomials defining the
equations;
![]() is the set of polynomials defining the
inequations in the complex case (resp. the inequalities
in the real case);
is the set of polynomials defining the
inequations in the complex case (resp. the inequalities
in the real case);
For any
u![]()
Cdlet
![]()
ube the specialization
![]() ;
;
![]() denotes the canonical projection on the
parameter's space
denotes the canonical projection on the
parameter's space
![]() ;
;
Given any ideal
Iwe denote by
![]() the associated (algebraic) variety. If a variety
is defined as the zero set of polynomials with
coefficients in
the associated (algebraic) variety. If a variety
is defined as the zero set of polynomials with
coefficients in
![]() we call it a
we call it a
![]() -algebraic variety; we extend naturally this
notation in order to talk about
-algebraic variety; we extend naturally this
notation in order to talk about
![]() -irreducible components,
-irreducible components,
![]() -Zariski closure, etc.
-Zariski closure, etc.
for any set
![]() ,
,
![]() will denote its
will denote its
![]() -Zariski closure in
-Zariski closure in
![]() .
.
In most applications,
![]() as well as
as well as
![]() are finite and not empty for almost all parameter's
are finite and not empty for almost all parameter's
u. Most algorithms that study
![]() or
or
![]() (number of real roots w.r.t. the parameters,
parameterizations of the solutions, etc.) compute in any
case a
(number of real roots w.r.t. the parameters,
parameterizations of the solutions, etc.) compute in any
case a
![]() -Zariski closed set
-Zariski closed set
![]() such that for any
such that for any
![]() , there exists a neighborhood
, there exists a neighborhood
![]() of
of
uwith the following properties :
![]() is an analytic covering of
is an analytic covering of
![]() ; this implies that the elements of
; this implies that the elements of
![]() do not vanish (and so have constant sign in the
real case) on the connected components of
do not vanish (and so have constant sign in the
real case) on the connected components of
![]() ;
;
We recently
show that the parameters' set
such that there doesn't exist any neighborhood
![]() with the above analytic covering property is a
with the above analytic covering property is a
![]() -Zariski closed set which can exactly be computed.
We name it the
minimal discriminant variety of
-Zariski closed set which can exactly be computed.
We name it the
minimal discriminant variety of
![]() with respect to
with respect to
![]()
Uand propose also a definition in the case of non
generically zero-dimensional systems.
Being able to compute the minimal discriminant variety
allows to simplify the problem depending on
nvariables to a similar problem depending on
dvariables (the parameters) : it is sufficient
to describe its complementary in the parameters' space (or
in the closure of the projection of the variety in the
general case) to get the full information about the generic
solutions (here generic means for parameters' values
outside the discriminant variety).
Then being able to describe the connected components of
the complementary of the discriminant variety in
![]() becomes a main challenge which is strongly linked to
the work done on positive dimensional systems. Moreover,
rewriting the systems involved and solving zero-dimensional
systems are major components of the algorithms we plan to
build up.
becomes a main challenge which is strongly linked to
the work done on positive dimensional systems. Moreover,
rewriting the systems involved and solving zero-dimensional
systems are major components of the algorithms we plan to
build up.
We currently propose several computational strategies. An a priori decomposition into equidimensional components as zeros of radical ideals simplifies the computation and the use of the discriminant varieties. This preliminary computation is however sometimes expensive, so we are developing adaptive solutions where such decompositions are called by need. The main progress is that the resulting methods are fast on easy problems (generic) and slower on the problems with strong geometrical contents.
The existing implementations of algorithms able to
"solve" (to get some information about the roots)
parametric systems do all compute (directly or indirectly)
discriminant varieties but none computes optimal objects
(strict discriminant variety). This is the case, for
example of the Cylindrical Algebraic Decomposition adapted
to
![]() , of algorithms based on
"Comprehensive Gröbner bases"
,
,
or of methods that compute
parameterizations of the solutions (see
for example). The consequence
is that the output (case distinctions w.r.t. parameters'
values) are huge compared with the results we can
provide.
, of algorithms based on
"Comprehensive Gröbner bases"
,
,
or of methods that compute
parameterizations of the solutions (see
for example). The consequence
is that the output (case distinctions w.r.t. parameters'
values) are huge compared with the results we can
provide.
A fundamental problem in cryptography is to evaluate the security of cryptosystems against the most powerful techniques. To this end, several generalmethods have been proposed: linear cryptanalysis, differential cryptanalysis, etc... Algebraic cryptanalysisis another general method which permits to study the security of the main public-key and secret-key cryptosystems.
Algebraic cryptanalysis can be described as a general framework that permits to asses the security of a wide range of cryptographic schemes. In fact the recent proposal and development of algebraic cryptanalysis is now widely considered as an important breakthrough in the analysis of cryptographic primitives. It is a powerful technique that applies potentially to a large range of cryptosystems. The basic principle of such cryptanalysis is to model a cryptographic primitive by a set of algebraic equations. The system of equations is constructed in such a way as to have a correspondence between the solutions of this system, and a secret information of the cryptographic primitive (for instance, the secret key of an encryption scheme).
Although the principle of algebraic attacks can probably be traced back to the work of Shannon, algebraic cryptanalysis has only recently been investigated as a cryptanalytic tool. To summarize algebraic attack is divided into two steps :
Modeling, i.e. representing the cryptosystem as a polynomial system of equations
Solving, i.e. finding the solutions of the polynomial system constructed in Step 1.
Typically, the first step leads usually to rather “big” algebraic systems (at least several hundreds of variables for modern block ciphers). Thus, solving such systems is always a challenge. To make the computation efficient, we usually have to study the structural properties of the systems (using symmetries for instance). In addition, one also has to verify the consistency of the solutions of the algebraic system with respect to the desired solutions of the natural problem. Of course, all these steps must be constantly checked against the natural problem, which in many cases can guide the researcher to an efficient method for solving the algebraic system.
Multivariate cryptographycomprises any cryptographic scheme that uses multivariate polynomial systems. The use of such polynomial systems in cryptography dates back to the mid eighties , and was motivated by the need for alternatives to number theoretic-based schemes. Indeed, multivariate systems enjoy low computational requirements and can yield short signatures; moreover, schemes based on the hard problem of solving multivariate equations over a finite field are not concerned with the quantum computer threat, whereas as it is well known that number theoretic-based schemes like RSA, DH, or ECDHare. Multivariate cryptosystems represent a target of choice for algebraic cryptanalysis due to their intrinsic multivariate repesentation.
The most famous
multivariate public key scheme is probably the Hidden Field
Equation (HFE) cryptosystem proposed by Patarin
. The basic idea of HFE is
simple: build the secret key as a univariate polynomial
S(
x)over some (big) finite field
(often
![]() ). Clearly, such a polynomial can be easily evaluated;
moreover, under reasonable hypotheses, it can also be
“inverted” quite efficiently. By inverting, we mean finding
any solution to the equation
). Clearly, such a polynomial can be easily evaluated;
moreover, under reasonable hypotheses, it can also be
“inverted” quite efficiently. By inverting, we mean finding
any solution to the equation
S(
x) =
y, when such a solution exists. The
secret transformations (decryption and/or signature) are
based on this efficient inversion. Of course, in order to
build a cryptosystem, the polynomial
Smust be presented as a public transformation which
hides the original structure and prevents inversion. This is
done by viewing the finite field
![]() as a vector space over
as a vector space over
![]() and by choosing two linear transformations of this
vector space
and by choosing two linear transformations of this
vector space
L1and
L2. Then the public transformation is the composition of
L1,
Sand
L2. Moreover, if all the terms in the polynomial
S(
x)have Hamming weight 2, then it is
obvious that all the (multivariate) polynomials of the public
key are of degree two.
By using fast
algorithms for computing Gröbner bases, it was possible to
break the first HFE challenge
(real cryptographic size 80 bits
and a symbolic prize of 500 US$) in only two days of CPU
time. More precisely we have used the
F5/2version of the fast
F5algorithm for computing Gröbner bases (implemented in
C). The algorithms available up to now (Buchberger) were
extremely slow and could not have been used to break the code
(they should have needed at least a few centuries of
computation). The new algorithm is thousands of times faster
than previous algorithms. Several matrices have to be reduced
(Echelon Form) during the computation: the biggest one has no
less than 1.6 million columns, and requires 8 gigabytes of
memory. Implementing the algorithm thus required significant
programming work and especially efficient memory
management.
The weakness of the
systems of equations coming from HFE instances can be
explainedby the algebraic properties of the secret key
(work presented at Crypto 2003 in collaboration with
A. Joux). From this study, it is possible to predict the
maximal degree occurring in the Gröbner basis computation.
This permits to establish precisely the complexity of the
Gröbner attack and compare it with the theoretical bounds.
The same kind of technique has since been used for
successfully attacking other types of multivariate
cryptosystems :
IP
,
2R
,
![]() -IC
, and MinRank
.
-IC
, and MinRank
.
On the one hand algebraic techniques have been successfully applied against a number of multivariate schemes and in stream cipher cryptanalysis. On the other hand, the feasibility of algebraic cryptanalysis remains the source of speculation for block ciphers, and an almost unexplored approach for hash functions. The scientific lock is that the size of the corresponding algebraic systems are so huge (thousands of variables and equations) that nobody is able to predict correctly the complexity of solving such polynomial systems. Hence one goal of the team is ultimately to design and implement a new generation of efficient algebraic cryptanalysis toolkits to be used against block ciphers and hash functions. To achieve this goal, we will investigate non-conventionalapproaches for modeling these problems.