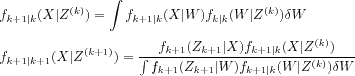The phrase “Decision under uncertainty” refers to the
problem of taking decisions when we do not have a full
knowledge neither of the situation, nor of the consequences
of the decisions, as well as when the consequences of
decision are non deterministic.
We introduce two specific sub-domains, namely the Markov
decision processes which models sequential decision problems,
and bandit problems.
Markov decision processes
Sequential decision processes occupy the heart of the
SequeLproject; a
detailed presentation of this problem may be found in
Puterman's book
A Markov Decision Process (MDP) is defined as the tuple
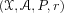 where
where
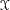 is the state space,
is the state space,
 is the action space,
is the action space,
Pis the probabilistic transition kernel, and
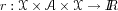 is the reward function. For the sake of simplicity,
we assume in this introduction that the state and action
spaces are finite. If the current state (at time
is the reward function. For the sake of simplicity,
we assume in this introduction that the state and action
spaces are finite. If the current state (at time
t) is
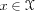 and the chosen action is
and the chosen action is
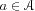 , then the Markov assumption means that the
transition probability to a new state
, then the Markov assumption means that the
transition probability to a new state
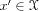 (at time
(at time
t+ 1) only depends on
(
x,
a). We write
p(
x'|
x,
a)the corresponding transition
probability. During a transition
(
x,
a)
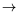
x
', a reward
r(
x,
a,
x')is incurred.
In the MDP (
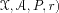 , each initial state
, each initial state
x0and action sequence
a0,
a1, ...gives rise to a sequence of states
x1,
x2, ..., satisfying
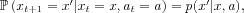 and rewards
Note that for simplicity,
we considered the case of a deterministic reward function,
but in many applications, the reward
and rewards
Note that for simplicity,
we considered the case of a deterministic reward function,
but in many applications, the reward
rtitself is a random variable.
r1,
r2, ...defined by
rt=
r(
xt,
at,
xt+ 1).
The history of the process up to time
tis defined to be
Ht= (
x0,
a0, ...,
xt-1,
at-1,
xt). A policy
 is a sequence of functions
is a sequence of functions
 0,
0,
 1, ..., where
1, ..., where

tmaps the space of possible histories at time
tto the space of probability distributions over the
space of actions
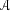 . To follow a policy means that, in each time step,
we assume that the process history up to time
. To follow a policy means that, in each time step,
we assume that the process history up to time
tis
x0,
a0, ...,
xtand the probability of selecting an action
ais equal to

t(
x0,
a0, ...,
xt)(
a). A policy is called stationary
(or Markovian) if

tdepends only on the last visited state. In other
words, a policy
 = (
= (
 0,
0,
 1, ...)is called stationary if
1, ...)is called stationary if

t(
x0,
a0, ...,
xt) =
 0(
0(
xt)holds for all
t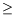 0. A policy is called deterministic
if the probability distribution prescribed by the policy
for any history is concentrated on a single action.
Otherwise it is called a stochastic policy.
0. A policy is called deterministic
if the probability distribution prescribed by the policy
for any history is concentrated on a single action.
Otherwise it is called a stochastic policy.
We move from an MD process to an MD problem by
formulating the goal of the agent, that is what the sought
policy
 has to optimize? It is very often formulated as
maximizing (or minimizing), in expectation, some functional
of the sequence of future rewards. For example, an usual
functional is the infinite-time horizon sum of discounted
rewards. For a given (stationary) policy
has to optimize? It is very often formulated as
maximizing (or minimizing), in expectation, some functional
of the sequence of future rewards. For example, an usual
functional is the infinite-time horizon sum of discounted
rewards. For a given (stationary) policy
 , we define the value function
, we define the value function
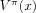 of that policy
of that policy
 at a state
at a state
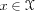 as the expected sum of discounted future rewards
given that we state from the initial state
as the expected sum of discounted future rewards
given that we state from the initial state
xand follow the policy
 :
:
![Im13 ${V^\#960 {(x)}=\#120124 \mfenced o=[ c=] \munderover \#8721 {t=0}\#8734 \#947 ^tr_t|x_0=x,\#960 ,}$](math_image_13.png)
where
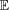 is the expectation operator and
is the expectation operator and
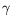
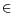 (0,
1)is the discount factor. This value function
(0,
1)is the discount factor. This value function
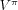 gives an evaluation of the performance of a given
policy
gives an evaluation of the performance of a given
policy
 . Other functionals of the sequence of future
rewards may be considered, such as the undiscounted reward
(see the stochastic shortest path problems
. Other functionals of the sequence of future
rewards may be considered, such as the undiscounted reward
(see the stochastic shortest path problems
In order to maximize a given functional in a sequential
framework, one usually applies Dynamic Programming
(DP)
V*(
x), defined as the optimal
expected sum of rewards when the agent starts from a state
x. We have
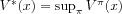 . Now, let us give two definitions about
policies:
. Now, let us give two definitions about
policies:
We say that a policy
 is optimal, if it attains the optimal values
is optimal, if it attains the optimal values
V*(
x)for any state
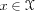 ,
i.e., if
,
i.e., if
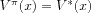 for all
for all
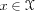 . Under mild conditions, deterministic
stationary optimal policies exist
. Under mild conditions, deterministic
stationary optimal policies exist
 *.
*.
We say that a (deterministic
stationary) policy
 is greedy with respect to (w.r.t.) some function
is greedy with respect to (w.r.t.) some function
V(defined on
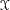 ) if, for all
) if, for all
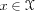 ,
,
![Im18 ${\#960 {(x)}\#8712 arg\munder max{a\#8712 \#119964 }\munder \#8721 {x^'\#8712 \#119987 }p{(x^'|x,a)}\mfenced o=[ c=] r{(x,a,x^')}+\#947 V{(x^')}.}$](math_image_18.png)
where
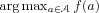 is the set of
is the set of
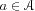 that maximizes
that maximizes
f(
a). For any function
V, such a greedy policy always exists because
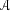 is finite.
is finite.
The goal of Reinforcement Learning (RL), as well as that
of dynamic programming, is to design an optimal policy (or
a good approximation of it).
The well-known Dynamic Programming
equation (also called the Bellman equation) provides a
relation between the optimal value function at a state
xand the optimal value function at the successors
states
x'when choosing an optimal action: for all
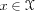 ,
,
![Im20 ${V^*{(x)}=\munder max{a\#8712 \#119964 }\munder \#8721 {x^'\#8712 \#119987 }p{(x^'|x,a)}\mfenced o=[ c=] r{(x,a,x^')}+\#947 V^*{(x^')}.}$](math_image_20.png)
The benefit of introducing this concept of optimal value
function relies on the property that, from the optimal
value function
V*, it is easy to derive an optimal behavior by
choosing the actions according to a policy greedy w.r.t.
V*. Indeed, we have the property that a policy greedy
w.r.t. the optimal value function is an optimal policy:
![Im21 ${\#960 ^*{(x)}\#8712 arg\munder max{a\#8712 \#119964 }\munder \#8721 {x^'\#8712 \#119987 }p{(x^'|x,a)}\mfenced o=[ c=] r{(x,a,x^')}+\#947 V^*{(x^')}.}$](math_image_21.png)
In short, we would like to mention that most of the
reinforcement learning methods developed so far are built
on one (or both) of the two following approaches (
Bellman's dynamic programming
approach, based on the introduction of the value
function. It consists in learning a “good”
approximation of the optimal value function, and then
using it to derive a greedy policy w.r.t. this
approximation. The hope (well justified in several
cases) is that the performance
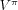 of the policy
of the policy
 greedy w.r.t. an approximation
greedy w.r.t. an approximation
Vof
V*will be close to optimality. This approximation
issue of the optimal value function is one of the major
challenge inherent to the reinforcement learning
problem.
Approximate dynamic programmingaddresses the
problem of estimating performance bounds (
e.g.the loss in performance
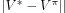 resulting from using a policy
resulting from using a policy
 -greedy w.r.t. some approximation
-greedy w.r.t. some approximation
V- instead of an optimal policy) in terms of the
approximation error
||
V
*-
V||of the optimal value
function
V*by
V. Approximation theory and Statistical Learning
theory provide us with bounds in terms of the number of
sample data used to represent the functions, and the
capacity and approximation power of the considered
function spaces.
Pontryagin's maximum principle
approach, based on sensitivity analysis of the
performance measure w.r.t. some control parameters.
This approach, also called
direct policy searchin the Reinforcement
Learning community aims at directly finding a good
feedback control law in a parameterized policy space
without trying to approximate the value function. The
method consists in estimating the so-called
policy gradient,
i.e.the sensitivity of the performance measure
(the value function) w.r.t. some parameters of the
current policy. The idea being that an optimal control
problem is replaced by a parametric optimization
problem in the space of parameterized policies. As
such, deriving a policy gradient estimate would lead to
performing a stochastic gradient method in order to
search for a local optimal parametric policy.
Finally, many extensions of the Markov decision
processes exist, among which the Partially Observable MDPs
(POMDPs) is the case where the current state does not
contain all the necessary information required to decide
for sure of the best action.
Bandits
Bandit problems illustrate the fundamental difficulty of
decision making in the face of uncertainty: A decision
maker must choose between what seems to be the best choice
(“exploit”), or to test (“explore”) some alternative,
hoping to discover a choice that beats the current best
choice.
The classical example of a bandit problem is deciding
what treatment to give each patient in a clinical trial
when the effectiveness of the treatments are initially
unknown and the patients arrive sequentially. These bandit
problems became popular with the seminal paper
Formally, a K-armed bandit problem (
K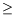 2) is specified by K real-valued
distributions. In each time step a decision maker can
select one of the distributions to obtain a sample from it.
The samples obtained are considered as rewards. The
distributions are initially unknown to the decision maker,
whose goal is to maximize the sum of the rewards received,
or equivalently, to minimize the regret which is defined as
the loss compared to the total payoff that can be achieved
given full knowledge of the problem,
i.e., when the arm giving the highest expected
reward is pulled all the time.
2) is specified by K real-valued
distributions. In each time step a decision maker can
select one of the distributions to obtain a sample from it.
The samples obtained are considered as rewards. The
distributions are initially unknown to the decision maker,
whose goal is to maximize the sum of the rewards received,
or equivalently, to minimize the regret which is defined as
the loss compared to the total payoff that can be achieved
given full knowledge of the problem,
i.e., when the arm giving the highest expected
reward is pulled all the time.
The name “bandit” comes from imagining a gambler playing
with K slot machines. The gambler can pull the arm of any
of the machines, which produces a random payoff as a
result: When arm k is pulled, the random payoff is drawn
from the distribution associated to k. Since the payoff
distributions are initially unknown, the gambler must use
exploratory actions to learn the utility of the individual
arms. However, exploration has to be carefully controlled
since excessive exploration may lead to unnecessary losses.
Hence, to play well, the gambler must carefully balance
exploration and exploitation. Auer
et al.
![]() to
to
![]() ,
,