Characterizing and inferring properties and behaviors of objects or phenomena from observations using models is common to many research fields. For dynamical systems encountered in the domains of engineering and physiology, this is of practical importance for monitoring, prediction, and control. For such purposes, we consider most frequently, the following model of dynamical systems:
![]()
where
x(
t),
u(
t)and
y(
t)represent respectively the
state, input and output of the system,
fand
gcharacterize the state and output equations,
parameterized by
![]() and subject to modeling and measurement
uncertainties
and subject to modeling and measurement
uncertainties
w(
t)and
v(
t). Modeling is usually based on
physical knowledge or on empirical experiences, strongly
depending on the nature of the system. Typically only the
input
u(
t)and output
y(
t)are directly observed by
sensors. Inferring the parameters
![]() from available observations is known as system
identification and may be useful for system monitoring
, whereas algorithms for
tracking the state trajectory
from available observations is known as system
identification and may be useful for system monitoring
, whereas algorithms for
tracking the state trajectory
x(
t)are called observers. The
members of SISYPHE have gained important experiences in the
modeling of some engineering systems and biomedical
systems. The identification and observation of such systems
often remain challenging because of strong nonlinearities
. Concerning control,
robustness is an important issue, in particular to ensure
various properties to all dynamical systems in some sets
defined by uncertainties
,
. The particularities of
ensembles of connected dynamical systems raise new
challenging problems.
Examples of reduced order models:
- Reduced order modeling of the cardiovascular system for signal & image processing or control applications. See section .
- Excitable neuronal networks & control of the reproductive axis by the GnRH. See section .
- Reduced order modeling of fuel cells for control and diagnosis applications. See section .
The real-life systems we consider, can be modeled (at least for some of their sub-systems) as networks of (almost identical) dynamical systems (NODS for short). Often, the available sensors provide information only at the macroscopic scale of the network. For example, usually in a fuel cell system, sensors measuring voltage and temperature are only available for the entire stack, not for individual cells. This sensor limitation implies challenging problems for the observation and control of such systems. The control objective may be formulated in terms of some kind of average behavior of the components and of bounds on some deviations from the average. To this end, appropriate modeling techniques must be developed.
The NODS are
intensively studied in physics and mathematics (see, e.g.
or
for a survey). This complex
structure gives rise to new dynamical behaviors, ranging
from de-correlation to coherent behaviors, such as
synchronization or emergence of traveling waves. New
control issues are also of particular interest as, here,
the problem of control of synchronization. We illustrate
this with an example of NODS where each dynamical system
iexchanges with the others,
j= 1...
N, in an additive way, a frequent
situation in our applications. A example of network based
on dynamical systems (
) is
:
![]()
The connectivity matrix
![]() represents the structure of the network.
represents the structure of the network.
NODS and Partial Differential Equations.
Semi-discretization in space of a PDE of evolution leads to NODS and in some situations, working with the PDE may be more efficient. Consider for example the NODS version of the first two equations of a cardiac cell model:
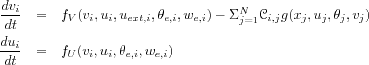
A particular case is the semi-discretization in space of a reaction-diffusion equation with no diffusion term for the intracellular state variables, the prototype being is the FitzHugh-Nagumo equation. For 3D computations as is the case in CardioSense3D, the PDE approach allows using well adapted discretization schemes.
![]()
For a fuel-cell stack with less than 50 cells, the NODS approach is interesting.
Consider now the dynamical
population of cells mentioned in section
. The coupling between cells is
due to the control and the NODS model, with
![]() and
and
Nvariable (depending upon the set of trajectories of
the cells in the age-maturity plane) corresponds to a
particle approximation of a controlled conservation law
,
where, for each follicle
f, the cell population is represented in each
cellular phase by a density
![]()
fand
ufand
Uare respectively a local control of follicle
fand a global control of all follicles:
![]()
Linear stationary waves.Our main example of
classical system that is interesting to see as a
quantum-like system is the Telegrapher Equation, a model of
transmission lines, possibly connected into a network. This
is the standard model for electrical networks, where
Vand
Iare the voltage and intensity functions of
zand
k, the position and frequency and
R(
z),
L(
z),
C(
z),
G(
z)are the characteristics of the
line:
![]()
Since the work of Noordergraaf
, this model is also used for
hemodynamic networks with
Vand
Irespectively the blood pressure and flow in vessels
considered as 1D media, and with
![]() ,
,
![]() ,
,
![]() where
where
![]() and
and
![]() are the density and viscosity of the blood ;
are the density and viscosity of the blood ;
r,
hand
Eare the inner radius, thickness and Young modulus of
the vessel.
S=
![]()
r2. The conductivity
Gis a small constant for blood flow.
Monitoring such networks is leading us
to consider the following inverse problem:
get information on the functions
R,
L,
C,
Gfrom the reflection coefficient
![]() (ratio of reflected over direct waves) measured
in some location by Time or Frequency Domain Reflectometry.
To study this problem it is convenient to use a Liouville
transform, setting
(ratio of reflected over direct waves) measured
in some location by Time or Frequency Domain Reflectometry.
To study this problem it is convenient to use a Liouville
transform, setting
![]() , to introduce auxiliary functions
, to introduce auxiliary functions
![]() and
and
![]() , so that (
) becomes a Zakharov-Shabat
system
that reduces to a Schrödinger
equation in the lossless case (
, so that (
) becomes a Zakharov-Shabat
system
that reduces to a Schrödinger
equation in the lossless case (
R=
G= 0):
![]()
and
![]() ,
,
![]() .
.
Our inverse problem becomes now an
inverse scattering problem for a Zakharov-Shabat (or
Schrödinger) equation:
find the potentials
q±and
qpcorresponding to
![]() . This classical problem of mathematical physics
can be solved using e.g. the Gelfand-Levitan-Marchenko
method.
. This classical problem of mathematical physics
can be solved using e.g. the Gelfand-Levitan-Marchenko
method.
Nonlinear traveling waves.In some recent publications , , we use scattering theory to analyze a measured Arterial Blood Pressure (ABP) signal. Following a suggestion made in , a Korteweg-de Vries equation (KdV) is used as a physical model of the arterial flow during the pulse transit time. The signal analysis is based on the use of the Lax formalism: the iso-spectral property of the KdV flow allows to associate a constant spectrum to the non stationary signal. Let the non-dimensionalized KdV equation be
![]()
In the Lax formalism,
yis associated to a Lax pair: a Schrödinger operator,
![]() and an anti-Hermitian operator
and an anti-Hermitian operator
![]() . The signal
. The signal
yis playing here the role of the potential of
L(
y)and is given by an operator
equation equivalent to (
):
![]()
Scattering and inverse scattering
transforms can be used to analyze
yin term of the spectrum of
L(
y)and conversely. The “bound
states” of
L(
y)are of particular interest: if
L(
y)is solution of (
) and
L(
y(
t))has only bound states (no
continuous spectrum), then this property is true at each
time and
yis a soliton of KdV. For example the arterial pulse
pressure is close to a soliton
.
Inverse scattering as a generalized Fourier
transform.For “pulse-shaped” signals
y, meaning that
![]() , the squared eigenfunctions of
, the squared eigenfunctions of
L(
y)and their space derivatives are
a basis in
![]() (see e.g.
) and we use this property to
analyze signals. Remark that the Fourier transform
corresponds to using the basis associated with
(see e.g.
) and we use this property to
analyze signals. Remark that the Fourier transform
corresponds to using the basis associated with
L(0). The expression of a signal
yin its associated basis is of particular interest.
For a positive signal (as e.g. the arterial pressure), it
is convenient to use
L(-
y)as
-
yis like a multi-well potential,
and the Inverse scattering transform formula becomes:
![]()
where
![]()
nand
f(
k, .)are solutions of
L(-
y)
f=
k2fwith
k=
i![]()
n,
![]()
n>0, for
![]()
n(bound states) and
k>0for
f(
k, .)(Jost solutions). The
discrete part of this expression is easy to compute and
provides useful informations on
yin applications. The case
![]() (
-
(
-
yis a reflectionless potential)
is then of particular interest as
2
Nparameters are sufficient to
represent the signal. We investigate in particular
approximation of pulse-shaped signals by such potentials
corresponding to N-solitons.
Interesting applications for quantum control have motivated seminal studies in such wide-ranging fields as chemistry, metrology, optical networking and computer science. In chemistry, the ability of coherent light to manipulate molecular systems at the quantum scale has been demonstrated both theoretically and experimentally . In computer science, first generations of quantum logical gates (restrictive in fidelity) has been constructed using trapped ions controlled by laser fields (see e.g. the "Quantum Optics and Spectroscopy Group, Univ. Innsbruck"). All these advances and demands for more faithful algorithms for manipulating the quantum particles are driving the theoretical and experimental research towards the development of new control techniques adapted to these particular systems. A very restrictive property, particular to the quantum systems, is due to the destructive behavior of the measurement concept. One can not measure a quantum system without interfering and perturbing the system in a non-negligible manner.
Quantum decoherence (environmentally induced dissipations) is the main obstacle for improving the existing algorithms . Two approaches can be considered for this aim: first, to consider more resistant systems with respect to this quantum decoherence and developing faithful methods to manipulate the system in the time constants where the decoherence can not show up (in particular one can not consider the back-action of the measurement tool on the system); second, to consider dissipative models where the decoherence is also included and to develop control designs that best confronts the dissipative effects.
In the first direction, we consider the Schrödinger
equation where
![]() (
(
t,
x),
![]() ,
,
V,
![]() and
and
u(
t)respectively represent the
wavefunction, the kinetic energy operator, the internal
potential, the dipole moment and the laser amplitude
(control field):
![]()
While the finite dimensional
approximations (
![]() ) have been very well studied (see e.g. the works by
H. Rabitz, G. Turinici, ...), the infinite dimensional case
(
) have been very well studied (see e.g. the works by
H. Rabitz, G. Turinici, ...), the infinite dimensional case
(
![]() ) remains fairly open. Some partial results on the
controllability and the control strategies for such kind of
systems in particular test cases have already been
provided
,
,
. As a first direction, in
collaboration with K. Beauchard (CNRS, ENS Cachan) et J-M
Coron (Paris-sud), we aim to extend the existing ideas to
more general and interesting cases. We will consider in
particular, the extension of the Lyapunov-based techniques
developed in
,
,
. Some technical problems, like
the pre-compactness of the trajectories in relevant
functional spaces, seem to be the main obstacles in this
direction.
) remains fairly open. Some partial results on the
controllability and the control strategies for such kind of
systems in particular test cases have already been
provided
,
,
. As a first direction, in
collaboration with K. Beauchard (CNRS, ENS Cachan) et J-M
Coron (Paris-sud), we aim to extend the existing ideas to
more general and interesting cases. We will consider in
particular, the extension of the Lyapunov-based techniques
developed in
,
,
. Some technical problems, like
the pre-compactness of the trajectories in relevant
functional spaces, seem to be the main obstacles in this
direction.
In the second direction, one needs to consider
dissipative models taking the decoherence phenomena into
account. Such models can be presented in the density
operator language. In fact, to the Schrödinger
equation (
), one can associate an
equation in the density operator language where
![]() =
=
![]()
![]() *represents the projection operator on
the wavefunction
*represents the projection operator on
the wavefunction
![]() (
[
(
[
A,
B] =
A
B-
B
Ais the commutator of the
operators
Aand
B):
![]()
Whenever, we consider a quantum system in its environment with the quantum jumps induced by the vacuum fluctuations, we need to add the dissipative effect due to these stochastic jumps. Note that at this level, one also can consider a measurement tool as a part of the environment. The outputs being partial and not giving complete information about the state of the system (Heisenberg uncertainty principle), we consider a so-called quantum filtering equation in order to model the conditional evolution of the system. Whenever the measurement tool composes the only (or the only non-negligible) source of decoherence, this filter equation admits the following form:
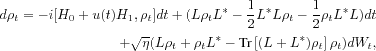
where
Lis the so-called Lindblad operator associated to the
measurement,
0<
![]()
![]() 1is the detector's efficiency and
where the Wiener process
1is the detector's efficiency and
where the Wiener process
Wtcorresponds to the system output
Ytvia the relation
![]() . This filter equation, initially introduced by
Belavkin
, is the quantum analogous of a
Kushner-Stratonovic equation. In collaboration with H.
Mabuchi and his co-workers (Physics department, Caltech),
we would like to investigate the derivation and the
stochastic control of such filtering equations for
different settings coming from different experiments
.
. This filter equation, initially introduced by
Belavkin
, is the quantum analogous of a
Kushner-Stratonovic equation. In collaboration with H.
Mabuchi and his co-workers (Physics department, Caltech),
we would like to investigate the derivation and the
stochastic control of such filtering equations for
different settings coming from different experiments
.
Finally, as a dual to the control problem, physicists
and chemists are also interested in the parameter
identification for these quantum systems. Observing
different physical observables for different choices of the
input
u(
t), they hope to derive more
precise information about the unknown parameters of the
system being parts of the internal Hamiltonian or the
dipole moment. In collaboration with C. Le Bris (Ecole des
ponts and INRIA), G. Turinici (Paris Dauphine and INRIA),
P. Rouchon (Ecole des Mines) and H. Rabitz (Chemistry
department, Princeton), we would like to propose new
methods coming from the systems theory and well-adapted to
this particular context. A first theoretical
identifiability result has been proposed
. Moreover, a first
observer-based identification algorithm is under study.
We consider networks or ensembles of cells of the same
type modeled by (
) with a single base model and
different parameters
![]()
i. In this case the solution of (
) may never live in the
synchronization manifold and it is of theoretical and
practical interest to study the deviations from this
manifold.
We are specially interested by large networks with a
particular structure, like e.g. possibly infinite binary
trees as it is the case for hemodynamic networks (e.g. the
coronary tree). When using thermodynamically consistent
reduced order models for the cells (e.g. cardiac cells and
coronary vessels for the heart or fuel cell systems) to model
the multiscale systems we want to study, a natural question
arises: what is the relation between the multiscale structure
of the
![]()
iand the structure of energy and information
u,
yamong scales? The inverse problem is the principal
motivation: gaining information on the
![]()
ifrom multiscale analysis of
y.
Two possible approaches for
describing the transfer of energy among scales are the
following: Looking at the way a given positive measure
![]() is distributed at the successive scales of regular
nested grids (denoted
is distributed at the successive scales of regular
nested grids (denoted
Gnat resolution
n), or looking at the manner the wavelet coefficients
of a square integrable function
gdecay to 0 along the scales. This can be done by
using ideas initially used by physicists in order to
describe the geometry of turbulence and then formalized by
mathematicians in the so-called multifractal formalism (
,
,
,
,
).
On the one hand one uses tools
coming from
statistical physicsand
large deviations theoryin order to describe
asymptotically for each singularity value
![]() the logarithmic proportion of cubes
the logarithmic proportion of cubes
Cin
Gn(the dyadic grid of level
n) such that the mass distributed in
Cis approximately equal to the power
![]() of the diameter of
of the diameter of
C, i.e.
![]() . This yields a sequence of functions
. This yields a sequence of functions
fnof
![]() called large deviation spectrum, which describes
statistically the heterogeneity of the distribution of the
measure at small scales. Another tool associated with this
spectrum consists in the partitions functions
called large deviation spectrum, which describes
statistically the heterogeneity of the distribution of the
measure at small scales. Another tool associated with this
spectrum consists in the partitions functions
![]()
They are Laplace transforms closely
related to the functions
fn.
The same quantities can be associated with the
L2function
gby replacing the masses
![]() (
(
C)by the wavelet coefficients
|
d
C(
g)|.
In practice, the functions
fnand
![]()
ncan be computed and are used to exhibit a scaling
invariance structure in a given signal as soon as they
remain quasi constant when
nranges in some non trivial interval. This approach
proves to be efficient in detecting scaling invariance in
energy dissipation and velocity variability in fully
developed turbulence
as well as in the heart-beat
variability
,
and in financial time series
. Scaling invariance in
heart-beat variability is one of our research directions
(see Section 3.2). It should reflect the heterogeneous
spatiotemporal distribution of the energy in the cardiac
cells and should be related to models of this
phenomenon.
On the other hand one uses tools
from
geometric measure theorysuch as Hausdorff measures
and dimensions in order to have a geometrical description
of the (fractal) sets of singularities
![]() obtained as the sets of those points
obtained as the sets of those points
xat which the sequences
![]() (
(
Cn(
x))or
|
d
Cn(
x)(
g)|behaves asymptotically like
![]() , where
, where
![]() is the sequence of nested cubes in the grids
is the sequence of nested cubes in the grids
Gnthat contain the point
x. The singularity spectrum obtained by computing the
Hausdorff dimension of the sets
![]() yields a finer description of the heterogeneity in
the energy distribution than the statistical one provided
by large deviations spectra. But this object is purely
theoretical since it necessitates the resolution to go
until
yields a finer description of the heterogeneity in
the energy distribution than the statistical one provided
by large deviations spectra. But this object is purely
theoretical since it necessitates the resolution to go
until
![]() .
.
Since the tools described above are efficient in physical and social phenomena, it is important to investigate models of measures and functions having such properties and develop associated statistical tools of identification. Such models do exist and have been studied for a long time ( , , , , , , , , , ) but few satisfactory associated statistical tools have been developed. We shall study new models of scaling invariant measures, signed multiplicative cascades, and wavelet series. In particular we will be inspired by the model proposed in of cascading mechanisms for the evolution of wavelet coefficients of the solution of the Euler equation. It could be used to construct a model for the multiscale control of cardiac cellular energetics and, as we already said above, a model for the heart-beat variability.
These works will contribute to one of the theoretical aspects developed in the team, which consists in studying and classifying statistically self-affine and multifractal mathematical objects.
Analysis of Heart Rate Variability (HRV), the
beat-to-beat fluctuations in heart rate, has many clinical
applications. The observation of the
1/
fshape of the HRV spectrum has
been strengthened recently by using techniques of
multifractal signals processing. These techniques quantify
a signal temporal irregularity for instance by constructing
an histogram of the “coarse-grained” Hölder exponents
computed on finer and finer nested grids. This leads to the
so-called large deviations spectrum, which describes the
frequency at which each Hölder exponent occurs. This is a
way to estimate variability. One can say that some scale
invariance holds when the large deviation spectrum weakly
depends on the scale in the nested grid. Such a scale
invariance has been observed on RR signals, and one
concluded that the largest the range of the exponents, the
better the patient's health. In particular the multifractal
large deviation spectrum is shown to be a useful tool to
study the long-term fluctuations for the diagnosis of some
pathologies like congestive heart failure.
HRV analysis can be completed
considering Blood Pressure Variability (BPV). For example
joint analysis of short-term HRV and BPV leads to the
baroreflex sensitivity (BRS), the gain of the
parasympathetic feedback loop, a useful index of
parasympathetic activity that has a prognostic value in
several situations (myocardial infarction, heart failure of
diabetic patients): low BRS is correlated with mortality in
patients with heart failure. In the case of BPV,
1/
fshaped spectra have also been
observed and it has been found that sympathetic nerve
traffic and BPV follow comparable self-similar scaling
relationships. In both case, HRV or BPV, the physiological
origins of these long-term fluctuations remain mysterious.
The goal of this study is to provide methods and tools to
improve variability analysis for a better understanding of
these fluctuations.
Our method will be to associate multiscale signal analysis and mathematical models whenever it will be possible. The ANR project DMASC has started in 2009 on these questions.
Understanding the complex mechanisms involved in the cardiac pathological processes requires fundamental researches in molecular and cell biology, together with rigorous clinical evaluation protocols on the whole organ or system scales. Our objective is to contribute to to these researches by developing low-order models of the cardiac mechano-energetics and control mechanisms, for applications in model-based cardiovascular signal or image processing.
We consider intrinsic heart control mechanisms, ranging from the Starling and Treppe effects (also called positive staircase effect) on the cell scale to the excitability of the cardiac tissue and to the control by the autonomous nervous system. They all contribute to the function of the heart in a coordinated manner that we want to analyse and assess. For this purpose, we study reduced-order models of the electro-mechanical activity of cardiac cells designed to be coupled with measures available on the organ scale (e.g. ECG and pressure signals). We study also the possibility to gain insight on the cell scale by using model-based multiscale signal processing techniques of long records of cardiovascular signals.
Here are some questions of this kind, we are considering:
- Modeling the controlled contraction/relaxation from molecular to tissue and organ scales.
- Direct and inverse modeling the electro-mechanical activity of the heart on the cell scale.
- Nonlinear spectral analysis of arterial blood pressure waveforms and application to clinical indexes.
- Modeling short-term and long-term control dynamics on the cardiovascular-system scale. Application to a Total Artificial Heart.
Modeling the controlled contraction/relaxation from molecular to tissue and organ scales.
We have obtained a controlled constitutive law of cardiac myofibre mechanics aimed at being embedded into 0D or 3D models . This law results from a model of the collective behavior of actin-myosin molecular motors converting chemical into mechanical energy . It is thermodynamically consistent and the resulting dynamics of sarcomeres is consistent with the “sliding filament hypothesis” of A. F. Huxley.
The model in
is currently used as the
constitutive law for the cardiac tissue in the
3
Dmodel of the heart developed in
the
CardioSense3Dproject. It is
useful for computing stress, strain and the action
potential fields when coupled with an electrical model
,
. Depending upon a small number
of parameters having a clear physical meaning, it is well
suited for the study of inverse problems as considered in
the CardioSense3D project (model-based 3D image
processing). In order to check the mathematical consistency
of our models, we have considered, in the more simple case
of a 1D geometry, the mathematical analysis of the fibre
model used in CardioSense3D based on the previous
constitutive law
).
Direct and inverse modeling the electro-mechanical activity of the heart on the cell scale.
We have revisited the ionic-currents models of cells representing membrane phenomena and calcium dynamics in order to reduce them for signal or image processing applications , , . An objective here, is to obtain invertible (depending upon available measurements) thermodynamically consistent models (the various ATP consumption have to be taken into account). This will allow in particular a better connection with the perfusion models developed in CardioSense3D.
We have studied an intrinsic control effect, represented by the restitution curve associated to a very simple cardiac cell model and estimated by ECG analysis.
For isolated and electrically excited cardiac cells, there is a well known relationship between each action potential duration (APD) and the preceding diastolic interval (DI) under the name of restitution curve. A similar relationship has been recently revealed between the QT interval and the preceding TQ interval computed from electrocardiogram (ECG) signals measured at the body surface . By analogy to the cellular restitution curve, we call this relationship ECG-based restitution curve. To successfully build this curve, the ECG signals must be recorded under some particular conditions. The isometric Handgrip test has proved to be a good choice for this purpose. It is also important to delimit the QT interval with a sufficient accuracy. For that purpose, we use the algorithm for T wave detection, whose robustness and efficiency have been reported in . In our previous work, the QT interval was obtained by adding a constant to the RT interval which is easier to delimit . More recently, in order to improve the delimitation of the QT interval, an algorithm for QRS onset detection has been developed. It is based on the computation of the envelop signal of the QRS defined with the Hilbert transform, and also on the application of a statistical detection algorithm. This new algorithm is now used for building ECG-based restitution curves , .
Nonlinear spectral analysis of arterial blood pressure waveforms and application to clinical indexes
We have proposed a reduced model of the input-output behaviour of an arterial compartment, including the short systolic phase where wave phenomena are predominant. A more detailed analysis is now available . The objective is to provide basis for model-based signal processing methods for the estimation from non-invasive measurements and the interpretation of the characteristics of these waves. We develop now the corresponding signal processing method and some applications.
This method, based on scattering transform for a one dimensional Schrödinger equation, provides new parameters, related to the systolic and diastolic parts of the pressure. They are compared to the classical blood pressure indexes in four conditions: moderate chronic heart failure, exercise before and after training in high fit triathlets , handgrip isometric exercise and orthostatic tilt test. . In each case these parameters are more significant than the classical ones. Moreover, they bring up new indexes, difficult to measure routinely: we think that the two first invariants might give information about the variation of the stroke volume and the ventricular contractility. At last, the first eigenvalue seems to reflect the baroreflex sensitivity in a certain way. We are now working on the validation of these hypotheses.
Modeling short-term and long-term control dynamics on the cardiovascular-system scale.
Our objective is to relate discrete-time (beat-to-beat) cardiovascular signal analysis to models of the cardiovascular and control systems taking into account its multiple feedback loop organisation. This will lead to a model-based signal processing approach for the estimation of the classical arterial-pressure/heart-rate baroreflex sensitivity and of several other discrete-time feedback loop sensitivities of practical interest. It will be also useful for the control of Artificial heart.
In the past we have used time-frequency techniques for these studies (Fourier Transform, spectral gain between the cardiac and blood pressure series, Smooth Pseudo Wigner_Ville Distribution, Complex DeModulation, temporal method of the cardiovascular Sequences). Different situations have been studied: the cardio-respiratory system dynamics in chronic heart failure , , ; the autonomic control of the cardiovascular system during sleep ; the effects of exercise intensity and repetition on heart rate variability during training , , . We will combine these techniques with our new inverse scattering approach. In particular the scattering-based description of cadiovascular signals leads to the definition of new indexes we want to investigate, see paragraph .
This approach is applied to the control of a Total Artificial Heart.
The ovulatory success is the main limiting factor of the whole reproductive process, so that a better understanding of ovulation control is needed both for clinical and zootechnical applications. It is necessary to improve the treatment of anovulatory infertility in women, as it can be by instance encountered in the PolyCystic Ovarian Syndrome (PCOS), whose prevalence among reproductive-age women has been estimated at up to 10%. In farm domestic species, embryo production following FSH stimulation (and subsequent insemination) enables to amplify the lineage of chosen females (via embryo transfer) and to preserve the genetic diversity (via embryo storage in cryobanks). The large variability in the individual responses to ovarian stimulation treatment hampers both their therapeutic and farming applications. Improving the knowledge upon the mechanisms underlying FSH control will help to improve the success of assisted reproductive technologies, hence to prevent ovarian failure or hyperstimulation syndrome in women and to manage ovulation rate and ovarian cycle chronology in farm species.
To control ovarian cycle and ovulation, we have to deeply understand the selection process of ovulatory follicles, the determinism of the species-specific ovulation rate and of its intra- and between-species variability, as well as the triggering of the ovulatory GnRH surge from hypothalamic neurons.
Beyond the strict scope of Reproductive Physiology, this understanding raises biological questions of general interest, especially in the fields of
Molecular and Cellular Biology.The granulosa cell, which is the primary target of FSH in ovarian follicles, is a remarkable cellular model to study the dynamical control of the transitions between the cellular states of quiescence, proliferation, differentiation, and apoptosis, as well as the adaptability of the response to the same extra-cellular signal according to the maturity level of the target cell. Moreover, the FSH receptor belongs to the seven transmembrane spanning receptor family, which represent the most frequent target (over 50%) amongst the therapeutic agents currently available. The study of FSH receptor-mediated signaling is thus not only susceptible to allow the identification of relaying controls to the control exerted by FSH, but it is also interesting from a more generic pharmacological viewpoint.
Neuroendocrinology and Chronobiology.The mechanisms underlying the GnRH ovulatory surge involve plasticity phenomena of both neuronal cell bodies and synaptic endings comparable to those occurring in cognitive processes. Many time scales are interlinked in ovulation control from the fastest time constants of neuronal activation (millisecond) to the circannual variations in ovarian cyclicity. The influence of daylength on ovarian activity is an interesting instance of a circannual rhythm driven by a circadian rhythm (melatonin secretion from the pineal gland).
Simulation and control of a multiscale conservation law for follicular cells
In the past years, we have designed a multiscale model of the selection process of ovulatory follicles, including the cellular, follicular and ovarian levels , . The model results from the double structuration of the granulosa cell population according to the cell age (position within the cell cycle) and to the cell maturity (level of sensitivity towards hormonal control). In each ovarian follicle, the granulosa cell population is described by a density function whose changes are ruled by conservation laws. The multiscale structure arises from the formulation of a hierarchical control operating on the aging and maturation velocities as well on the source terms of the conservation law. The control is expressed from different momentums of the density leading to integro-differential expressions.
Future work will take place in the REGATEproject and will consist in:
- predicting the selection outcome (mono-, poly-ovulation or anovulation / ovulation chronology) resulting from given combinations of parameters and corresponding to the subtle interplay between the different organs of the gonadotropic axis (hypothalamus, pituitary gland and ovaries). The systematic exploration of the situations engendered by the model calls for the improvement of the current implementation performances. The work will consist in improving the precision of the numerical scheme, in the framework of the finite volume method and to implement the improved scheme, basing by instance on the current routines designed within the Bearclaw ( http://www.amath.unc.edu/Faculty/mitran/bearclaw.html) academic environment,
- solving the control problems associated with the model. Indeed, the physiological conditions for the triggering of ovulation, as well as the counting of ovulatory follicles amongst all follicles, define two nested and coupled reachability control problems. Such particularly awkward problems will first be tackled from a particular approximation of the density, in order to design appropriate control laws operating on the particles and allowing them to reach the target state sets.
Connectivity and dynamics of the FSH signaling network in granulosa cells
The project consists in analyzing the connectivity and
dynamics of the FSH signaling network in the granulosa
cells of ovarian follicles and embedding the network within
the multiscale representation described above, from the
molecular up to the organic level. We will examine the
relative contributions of the G
![]()
sand
![]() arrestin-dependent pathways in response to FSH
signal, determine how each pathway controls downstream
cascades and which mechanisms are involved in the
transition between different cellular states (quiescence,
proliferation, differentiation and apoptosis). On the
experimental ground, we propose to develop an antibody
microarray approach in order to simultaneously measure the
phosphorylation levels of a large number of signaling
intermediates in a single experiment. On the modeling
ground, we will use the BIOCHAM (biochemical abstract
machine) environment first at the boolean level, to
formalize the network of interactions corresponding to the
FSH-induced signaling events on the cellular scale. This
network will then be enriched with kinetic information
coming from experimental data, which will allow the use of
the ordinary differential equation level of BIOCHAM. In
order to find and fine-tune the structure of the network
and the values of the kinetic parameters, model-checking
techniques will permit a systematic comparison between the
model behavior and the results of experiments. In the end,
the cell-level model should be abstracted to a much simpler
model that can be embedded into a multiscale one without
losing its main characteristics.
arrestin-dependent pathways in response to FSH
signal, determine how each pathway controls downstream
cascades and which mechanisms are involved in the
transition between different cellular states (quiescence,
proliferation, differentiation and apoptosis). On the
experimental ground, we propose to develop an antibody
microarray approach in order to simultaneously measure the
phosphorylation levels of a large number of signaling
intermediates in a single experiment. On the modeling
ground, we will use the BIOCHAM (biochemical abstract
machine) environment first at the boolean level, to
formalize the network of interactions corresponding to the
FSH-induced signaling events on the cellular scale. This
network will then be enriched with kinetic information
coming from experimental data, which will allow the use of
the ordinary differential equation level of BIOCHAM. In
order to find and fine-tune the structure of the network
and the values of the kinetic parameters, model-checking
techniques will permit a systematic comparison between the
model behavior and the results of experiments. In the end,
the cell-level model should be abstracted to a much simpler
model that can be embedded into a multiscale one without
losing its main characteristics.
Bifurcations in coupled neuronal oscillators.
We have proposed a mathematical model allowing for the alternating pulse and surge pattern of GnRH (Gonadotropin Releasing Hormone) secretion . The model is based on the coupling between two systems running on different time scales. The faster system corresponds to the average activity of GnRH neurons, while the slower one corresponds to the average activity of regulatory neurons. The analysis of the slow/fast dynamics exhibited within and between both systems allows to explain the different patterns (slow oscillations, fast oscillations and periodical surge) of GnRH secretion.
This model will be used as a basis to understand the control exerted by ovarian steroids on GnRH secretion, in terms of amplitude, frequency and plateau length of oscillations and to discriminate a direct action (on the GnrH network) from an indirect action (on the regulatory network) of steroids. From a mathematical viewpoint, we have to fully understand the sequences of bifurcations corresponding to the different phases of GnRH secretion. This study will be derived from a 3D reduction of the original model.