Section: New Results
Application of shape and topology design to biology and medicine
Mathematical modeling of dorsal closure DC
Participants : Abderrahmane Habbal, Luis Almeida [University of Nice-Sophia Antipolis] , Patrizia Bagnerini [Genova University] , Fanny Serman [University of Nice-Sophia Antipolis] , Stéphane Noselli [University of Nice-Sophia Antipolis] , Glenn Edwards [Duke University] .
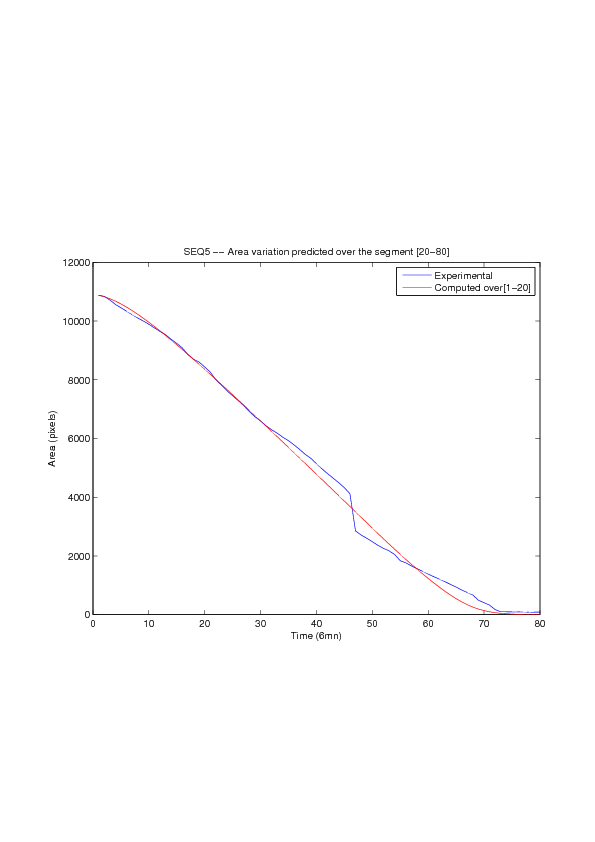
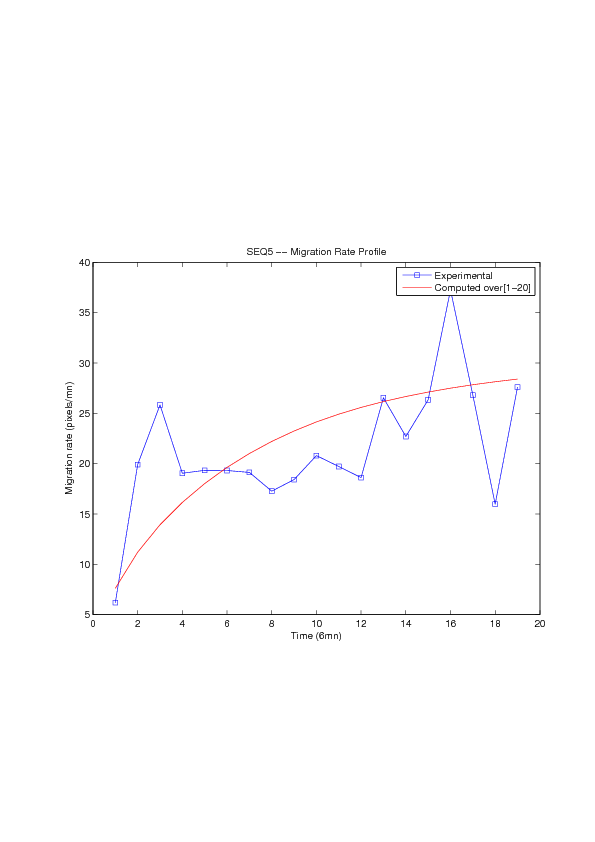
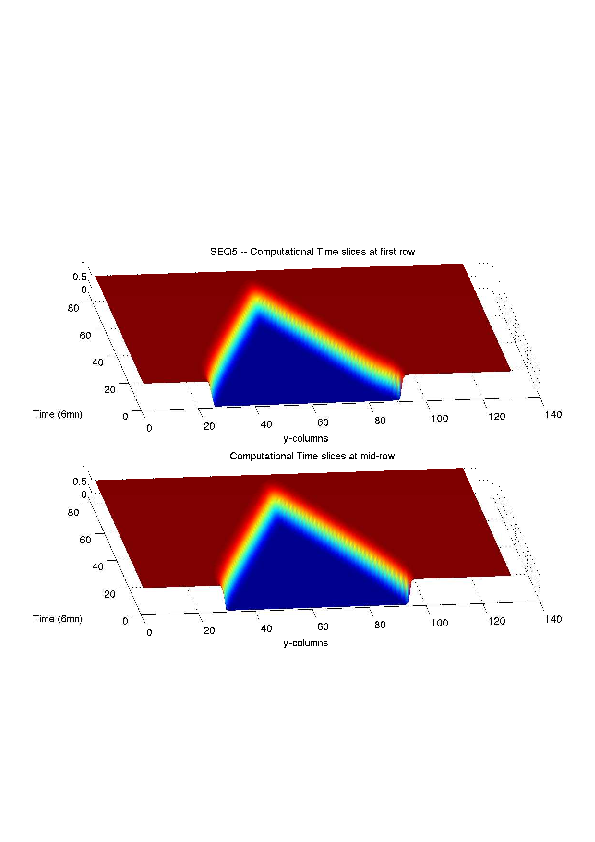
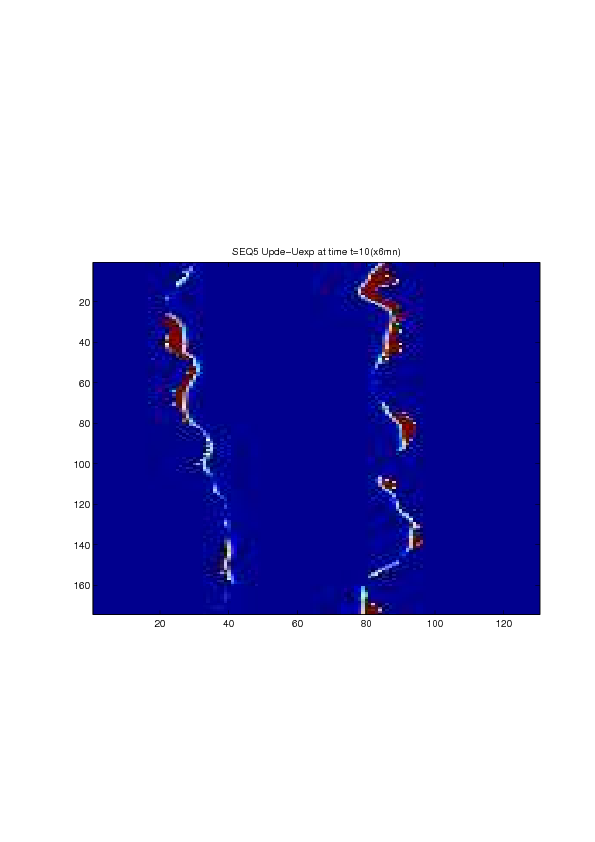
A mathematical model for simulation of actin cable contraction, during wound closure for Drosophila embryo, which contains an extra term in addition to the curvature flow is developed. The basic mathematical model introduced and validated in [2] is extended in order to include the non-homogeneous wound healing or non-homogeneous dorsal closure The new model is obtained by adding extra terms that describe the particular process we want to model (lamellipodial crawling, granulation tissue contraction, extension of actin protrusions, epithelial resistance, etc.). We concentrate on the treatment of non-homogeneous forces, i.e. non-constant boundary terms which can be associated with a non-uniform cable, internal pull or zipping force due to the non-uniformity of the biological or physical properties of the boundary cells or of the connective tissue [35] .
We also consider a particular yet major aspect of wound healing, namely the one related to the movement of wounded epithelial cell monolayers. The epithelial monolayer cell population, also referred to as cell-sheet, can be seen as a 2 dimensional structure, although it is well known that apical and basal sites play distinctive important roles during the migration, as well as the substrate itself. Immediately after a wound is created, the cells start to move in order to fill in the empty space. This movement, the wound closure, is a highly-coordinated collective behavior yielding a structured cohesive front, the wound leading edge. Even though wound closure involves biochemical and biomechanical processes, still far from being well understood, which are distributed over the whole monolayer, much specific attention was paid to the leading edge evolution, seen as the front of a traveling wave of the cell density function. We show that, for non inhibited wound assays, closure occurs at constant speed of the leading edge, a fact that is commonly shared by biologists and biomathematicians. But we also show that the leading edge may exhibit accelerated profiles, and that when inhibited, then the F-KPP has poor performances in modeling the leading edge dynamics.
|