Section: Research Program

Stroke

Project team positioning

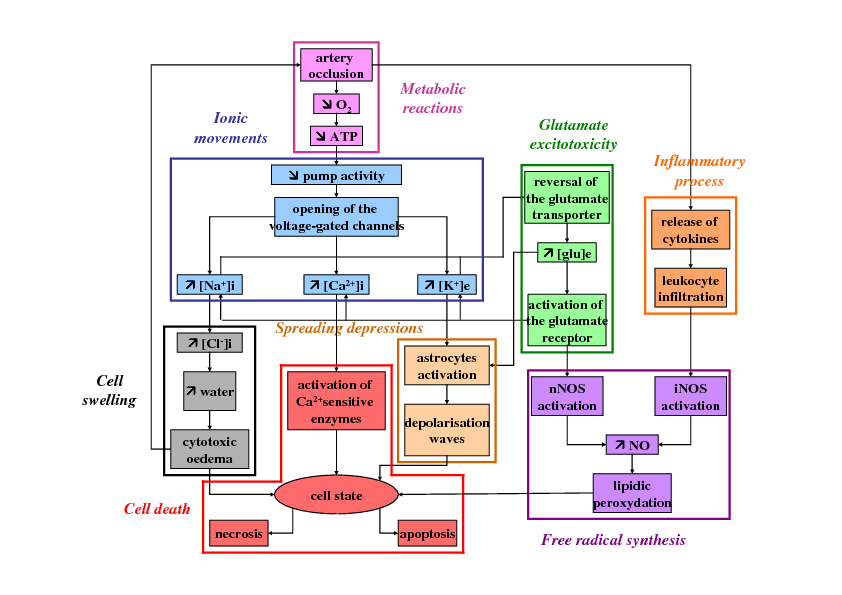
Stroke is a major public health problem since it represents the second leading cause of death worldwide and the first cause of acquired disability in adults. In the United States, this disease strikes once every 40s and causes death every 4 minutes, with an estimated 41.6% death rate in 2007. Most frequently (80%) strokes result from the occlusion of one or several brain vessels and are thus called ischemic strokes (in the other cases, strokes are hemorrhagic strokes). Ischemic stroke involves many pathophysiological mechanisms causing devastating neurological damage (see Figure 1). Understanding these mechanisms is of the most importance to develop new therapeutic strategies since no treatment are currently available for most stroke patients. Currently, the only FDA-approved treatment for stroke patients is a thrombolytic agent (tPA) which can only be given to less than 10% of patients because of its narrow time-window and its hemorrhagic risks. Many neuroprotective agents (aimed at blocking the ischemic cascade) have also been developed but, although they had given very promising results in preclinical studies in rodent models, they appeared ineffective or even noxious during the clinical trials in stroke patients. This discrepancy between the results in rodents and in humans is partly due to the anatomic and histological differences between rodent and human brains. In this case, results in rodents are thus difficult to extrapolate to stroke patients. As a consequence, a mathematical model and its numerical simulations can help both to test some biological hypotheses concerning the involved mechanisms and to give new insights concerning the effects of these neuroprotective agents.

Before 2009, we had mainly developped models based on the precocious mechanisms of stroke: ionic movements (Dronne et al., 2006; Dronne et al., 2007; Dronne et al., 2008) and propagation of spreading depressions (Grenier et al., 2008; Chapuisat et al., 2008; Descombes and Dumont, 2008). Since 2009, we have continued working on the propagation of spreading depressions in stroke (Dronne et al., 2009; Chapuisat et al., 2010, Grenier et al, 2010, Dumont et al, 2013) and we have developped other sub-models of some pathophysiological mechanisms of stroke such as several models of inflammation (Lelekov-Boissard et al., 2009; Di Russo et al., 2010, two papers in preparation), a model of free radical synthesis (one paper in preparation) and a model of brain energy metabolism in stroke (one paper in preparation). We have studied and qualitatively validated these models and have used them to carry out in silico experiments to study and to better understand these biological mechanisms and the relative treatments.

Note that this axe of Numed had to face several difficulties. The former advisor of Marie Aimée Dronne created a start up in this domain in 2009. As a result, we have lost some of our medical collaborators, creating an important gap between the physicians and the other scientists involved in this project. Another problem was the fact that the leader of the project, Marie-Aimée Dronne, had huge teaching tasks due to the series of reforms in pharmaceutical studies and was stopped for maternity leave.

Results

A - Model of cell death

We have built a model of cell death during stroke. This model is focused on the main features of necrosis and apoptosis and their consequences on the surrounding brain tissue. The main variables of the model are energy supply and released toxicity and the reactions are described with partial differential equations (PDE). The aims of this model are to study the role of apoptosis and to explore the effects of anti-apoptotic drugs in stroke patients.

Biological issue

During a stroke, the ischemic cascade leads brain cells towards cell death, mainly towards necrosis and apoptosis. Necrosis is a fast and passive cell death involving cells with low ATP-level. Moreover, as necrosis is also responsible for the release of the cytoplasmic content in the extracellular space, it contributes to ischemic damage in the surrounding tissue. On the contrary, apoptosis is an active cell death involving cells with higher ATP supply. Contrary to necrotic cells, apoptotic bodies don't release intracellular constituents and are not accompanied by inflammatory response and surrounding tissue damage. Another feature of the apoptotic process is that two "stages" can be distinguished: the first one is a reversible stage during which the cell is still able to recover and the second one is the irreversible stage during which the cell will finally die. During a stroke, necrosis is observed mainly in the cells located in the infarcted core whereas apoptosis is observed mainly in the cells located in the surrounding area called penumbra. In order to salvage the penumbra, several anti-apoptotic approaches have been studied in rodent models. Some strategies were aimed at indirectly activate the anti-apoptotic activity of Bcl-2 and others were aimed at inhibiting the activities of some caspases. But these approaches encounter problems of use and bioavailability. Moreover, they appeared to be effective during a focal or a transient ischemia but not during global ischemia. Because of all these reasons, anti-apoptotic strategies haven't reach clinics yet. However, these strategies are interesting and would need more studies. Our model is thus aimed at studying the apoptosis process during ischemia depending on the size of the lesion with and without anti-apoptotic treatment.

Model and method

Our model is a qualitative model describing cell death at a global scale. The model takes into account three states of the cells: live cells, apoptotic cells (in the irreversible stage) and necrotic cells. The input variable is energy which represents the cerebral blood flow and the variable which describes the diffusion of the damage is toxicity (due to necrotic cells). The main variables are: Entropy, Apoptotic state and Toxicity. The corresponding equations are partial differential equations and more precisely reaction-diffusion equations.

Results

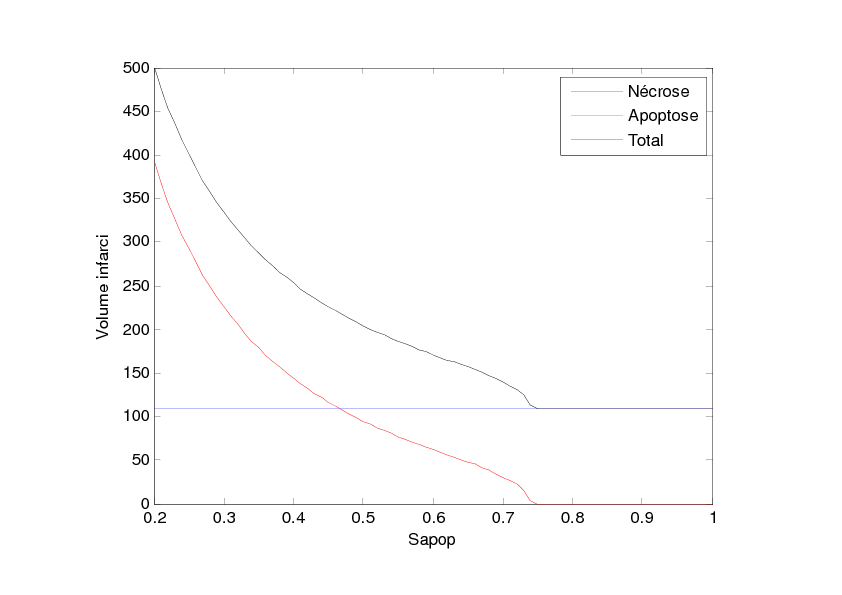
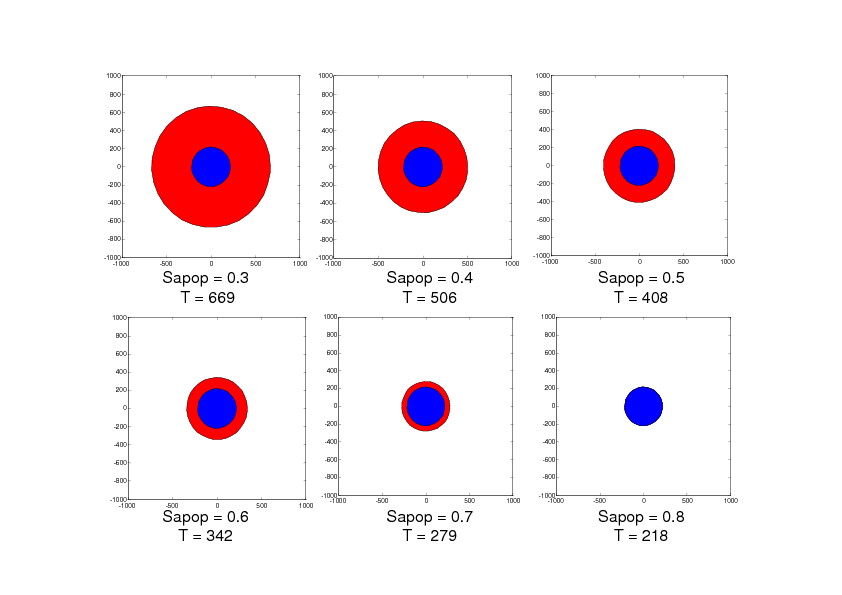
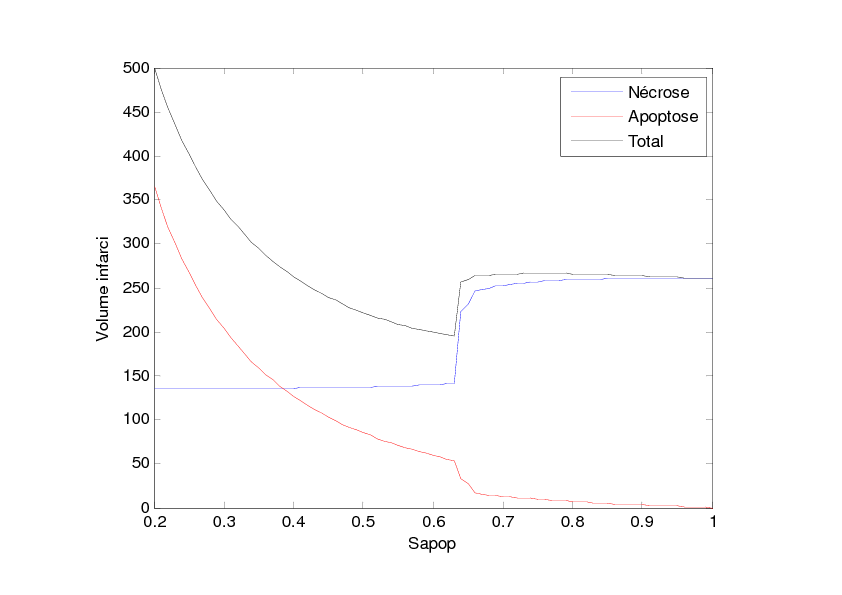
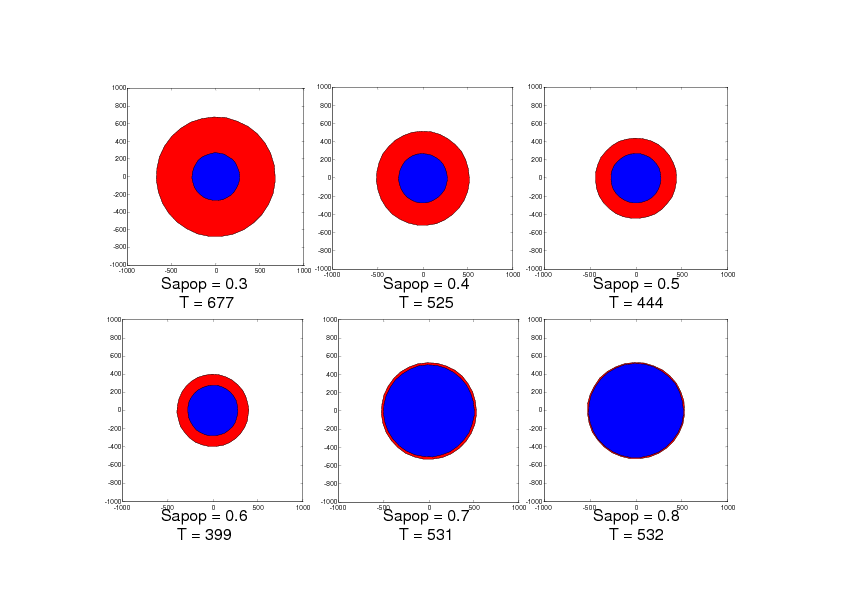
With this model, we have studied the influence of the value Sapop. This value is the entropy threshold over which the cell enters the irreversible stage of apoptosis. This value is all the more important as the anti-apoptotic strategies are supposed to increase this threshold. We have performed this study in two situations: the first situation describes damage extension in a stroke of small size as can be observed in rodent models and the second situation describes damage extension in a stroke of larger size as can be observed in stroke patients. The simulation results are given in Figures 2 and 3. Figure 2 shows that when Sapop increases in the case of stroke of small size, the number of cells which die from apoptosis decreases and thus, the volume of dead cells decreases. Figure 3 shows a more complex situation in the case of stroke of larger size. In this case, there is a value of Sapop which minimizes the volume of dead volume. Over this value, the volume of dead area increases with Sapop.

Conclusion

These simulation results suggest that, in the case of small stroke (as in rodent models), it would always be interesting to increase the "resistance" of the cells to apoptosis with anti-apoptotic strategies while, in the case of larger stroke (as in stroke patients), it could be interesting to increase the "resistance" of the cells to apoptosis with anti-apoptotic strategies but it would also be important to avoid blocking the apoptotic process since apoptosis has also a protecting role by "absorbing" the toxicity due to the necrotic cells.

B - Inflammation

We have developed several models of the inflammatory process in stroke. Two preliminary models have been built and two others are currently under study. These models takes into account the main molecules (cytokines, NO) and the main cells (microglial cells, neutrophiles and macrophages) involved in this process. They are based either on ODE or on PDE. They are all aimed at studying the complex role of the inflammatory process during a stroke and at studying the influence of some anti-inflammatory strategies in stroke patients.

Biological issue

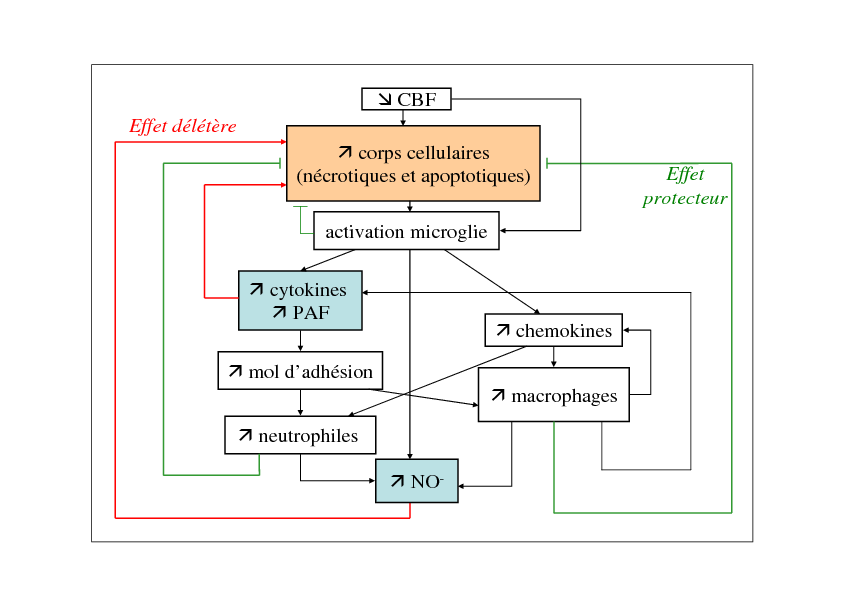
During a stroke, the cerebral blood flow decreases, which results in the death of brain cells firstly through necrotic process. Necrotic cells release intracellular components, resulting in an inflammatory reaction. Microglial cells are activated and produce cytokines, chemokines and other molecules (such as PAF). As a consequence, neutrophiles and macrophages are attracted and begin to infiltrate brain tissue through adhesion molecules. These inflammatory cells produce NO and also cytokines and chemokines to attract other inflammatory cells. These cells have also phagocytic properties and are able to phagocytize damage cells. As a consequenec, the inflammatory process has a dual role: on one hand, it is responsible for the release of toxic molecules (such as NO and some cytokines) and, on the other hand, it decreases the number of necrotic bodies. These mechanisms are represented in Figure 4.

Model 1:

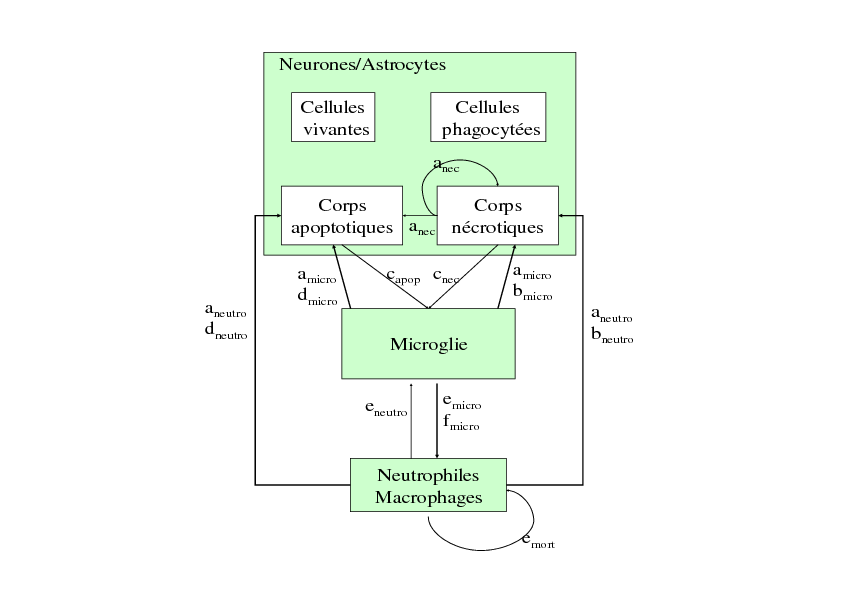
This model is focused on the cells involved in the inflammatory process. It takes into account the inflammatory cells (microglial cells, macrophages and neutrophiles) and the "target" cells (neurons, astrocytes) which can die through necrosis or apoptosis. The relationships between these cells are represented in Figure 5. This model is based on a set of 6 ODE. Its aims were to qualitatively study the dual role of inflammation and to differentiate the role of the precocious inflammation (through microglial activation) and the role of the late inflammation (through neutrophile and macrophage infiltration) by simulating the effect of different anti-inflammatory drugs. The simulation results show that when neutrophile infiltration is blocked, the number of dead cells decrease. The results are the same when the production of cytokines and NO is inhibited. These simulation results suggest the deleterious role of neutrophile infiltration and of the production of cytokines and NO. The role of microglial cells appears to be more complex. The simulation results show that the inhibition of microglial activity as well as the increase of phagocytic activity of microglial cells decrease the number of dead cells. All these results are described in a publication (Lelekov-Boissard et al., 2009). As a consequence, this model gave some preliminary interesting results but need improvements in order to take into account more quantitative aspects and diffusion aspects.

Model 2:

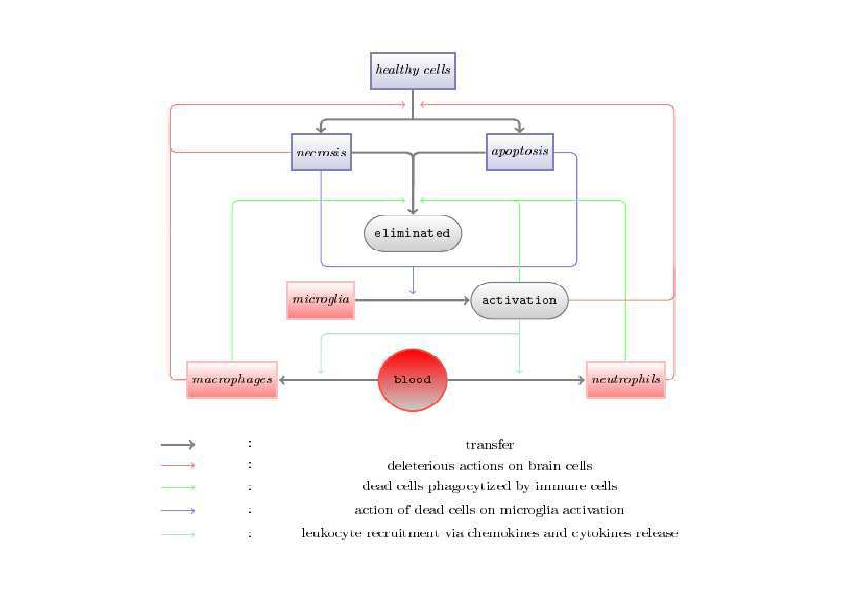
This model is also a cellular model focused on the cells involved in the inflammatory process (Figure 6) but it also take into account the spatial reactions through diffusion and attraction of cells. This model is based on a set of 13 equations (including 7 ODE and 4 PDE) . Two equations are equations of chemotaxis and 2 equations are reaction-diffusion equations. This model was aimed at qualitatively studying the spatial and temporal evolutions of the density of the inflammatory cells and of the concentrations of the inflammatory molecules during a stroke. And it was aimed at studying the influence of the size of the ischemic area on cell death due to the inflammatory process. This model gives rise to a mathematical study and to studies of sensibility and robustness. The simulation results show that when the initial ischemic area is small, the number of cells dead by inflammation is much less important than when the initial ischemic area is larger. These results suggest that the size of the initial stroke has an influence on the extension and the severity of the inflammatory process. All these results are discussed in a publication (Di Russo et al, 2010). As a consequence, this model gives complementary results as the first model presented above but it is always a qualitative model which needs other quantitative data to be improved and to be better validated.

Model 3:

This model is under study. It takes into account 4 variables: two variables for the state of the target cells (alive or dead), another for the inflammatory cells (microglial cells, macrophages and neutrophiles) and the last one for the inflammatory molecules (pro-inflammatory cytokines, chemokines, NO). The model is based on a set of 4 ODE in which the two stages of inflammation are distinguished and in which the cells can be alive, dead or phagocytized. The aim of this study is to use the quantitative data obtained by Maria Grazia de Simoni (Neurosciences, Mario Negri Institute, Milan, Italy) and funded by the ANR "AVC-in silico" project (2006-2009) for the parametrisation and the validation of the model. The model is then aimed at studying the time evolution of the inflammatory process in different situations: in moderate or severe ischemia and with various anti-inflammatory molecules. The simulation results show that the infiltration of neutrophiles and macrophages is all the more important as the ischemic lesion is severe. It also shows other more surprising results: The blockade of the infiltration of neutrophiles and macrophages appears to be more beneficial during moderate than during severe ischemia whereas inhibiting the cytokines is always beneficial whatever the severity of ischemia. These results are qualitative results and the quantitative study of the model needs to be continued. Even if the model has been built with the advise of the scientists who carried out the experiments, the data obtained with these experiments are difficult to exploit because the measured entities don't match the variables of the model. This work is thus under progress.

Model 4:

This model is based on the equations and the parameters used in model 3 but it also takes into account some spatial aspects in order to describe the diffusion of cytokines and the attraction of neutrophiles and macrophages by chemokines. This model thus contains one equation of chemotaxis and one reaction-diffusion equation. As the previous model, it is aimed at studying the effect of the severity of ischemia on cell death through inflammation and at studying the effect of various anti-inflammatory molecules. Meanwhile, numerical methods have been developed in order to use this model on a realistic brain geometry. The aim is to validate this model with medical images (RM images). Some collaborations have been initiated and will be developed with different scientists working in CREATIS (Marlr̀ene Wiart, David Rousseau).

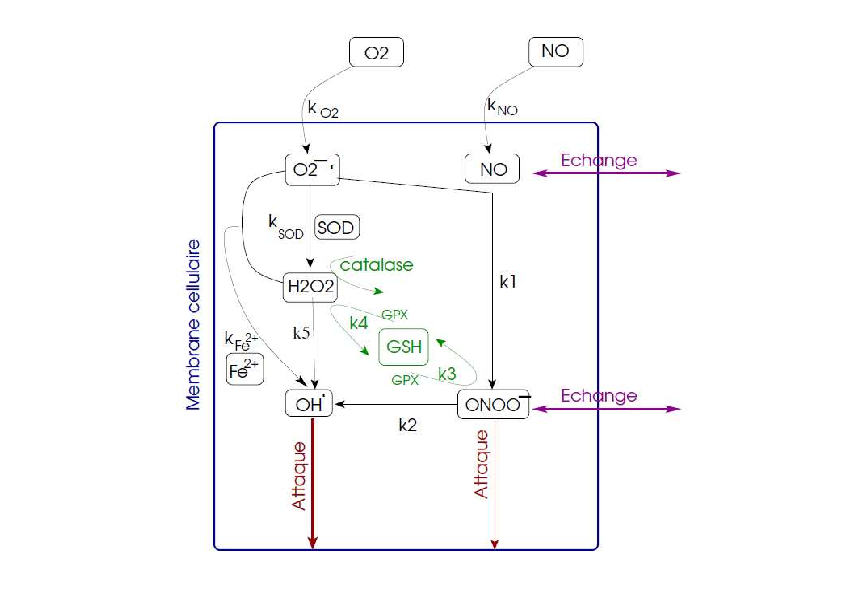
C - Model of free radicals

We have built a model focused on the free radical synthesis. This model takes into account the main free radicals involved during a stroke: NO, O2-., ONOO-, H2O2 and OH. and it also takes into account some protecting mechanisms such as glutathion and some enzymes. The chemical reactions are described with non linear ordinary differential equations (ODE). The aims of this model are to study this process and its influence on cell damage during a stroke and to carry out in silico experiments with various free radical scavengers.

Biological issue

During a stroke, some free radicals are produced and they will contribute to the degradation of cell state. First of all, some NO is produced in the endothelial cells (through the eNOS) in order to vasodilate the vessel. This production is precocious and rather beneficial. But, after several minutes, much more NO is produced by nNOS in the neurons and by iNOS in neutrophils which have been infiltrating the lesion area. This large production of NO will be all the more deleterious as it will combine with O2-. to produce some ONOO- which are known to degrade membranes, DNA and proteins of the cells and to lead the cells towards cell death. The high production of O2-. is mainly due to the dysfunction of the respiratory chain and is amplified during a transient stroke. It will combine with NO to produce ONOO- but it will also produce H2O2 and OH. with is highly deleterious for cells. Some protecting mechanisms try to limit the production of some free radicals such as glutathion (GSH) and some enzymes (SOD and catalase) but, during a stroke and especially during a transient stroke, these mechanisms are overwhelmed. Figure 7 represents these mechanisms.

Model and first results

The variables of the model are the free radicals and the protecting mechanisms described above. The model inputs are the production of NO and the entry of oxygen. The model outputs are ONOO- and OH. which are the most noxious free radicals. The chemical reactions are described with a set of ten non linear ordinary differential equations. Most of the chemical constants can been obtained in the literature from experimental studies. However, the input variables of the model and the initial conditions are difficult to quantify. As a consequence, the study of the model has first been a qualitative study. First of all, we studied the time evolution of the production of ONOO- and of OH. in two cases: a permanent stroke and a transient stroke. The results show that, during a permanent stroke, ONOO- decreases and OH. increases while, during a transient stroke, ONOO- increases as well as OH. We also carried out in silico experiments by simulating the effect of Edaravone which is a free-radical scavenger which has been used in clinical trials in stroke patients.

Conclusion

These simulation results suggest that, during a permanent stroke, some noxious free radicals are produced but, in the meantime, the protecting mechanisms are stimulated and block the production of some other free radicals. On the contrary, during a transient stroke, the simulation results suggest that the production of all free radicals is increased. These first qualitative results have to be further explored and quantitative data have to be used to validate the model.

D - Spreading depressions

Biological issue

During a stroke, waves of spreading depressions are triggered from the infarcted core. They are supposed to contribute to the extension of ishemic damage. They can be observed in the grey matter of stroke patients with medical imaging. Before 2009, we have already worked on models focused on these spreading depressions (Grenier et al., 2008; Chapuisat et al., 2008; Descombes and Dumont, 2008). Since 2009, we have continued working on models of these depolarisation waves in stroke (Dronne et al., 2009; Chapuisat et al., 2010, Grenier et al, 2010, Dumont et al, 2013). These models are all based on reaction-diffusion equations and are mainly phenomenological models aimed at studying the extension of the damage due to these spreading depressions on realistic geometries of human brain.

Phenomenological models

These models gave rise to mathematical and numerical studies. Two of these models explored the influence of the geometry on the propagation of these waves (Dronne et al, 2009; Grenier et al, 2010). Another model was used to study the influence of intensity and duration of blood flow reduction on cell death during the propagation of these waves (Chapuisat et al, 2010). Another model was a mathematical study on the extension of the necrotic area due to these spreading depressions (Grenier et al, 2010).

Mechanistic model on realistic 3D geometry

The last model (Dumont et al, 2013) is a mechanistic model involving the ionic movements, glutamate excitotoxicity, cytotoxic oedema and spreading depressions and is based on a previous model (Dronne et al., 2006; Dronne et al., 2007). It thus focuses on the first hour of a stroke, when the ionic exchanges are the main mechanisms leading to cell death. In this model, brain tissue is composed of two cell types, namely neurons and glial cells, and of extracellular space. Two domains are considered: the white and the grey matter which differ in their glial cell composition (astrocytes in grey matter and oligodendrocytes in white matter) and in their "neuronal area" composition (neuronal somas in grey matter and neuronal axons in white matter). Human brain cortex is exclusively composed of grey matter whereas human brain medium is mainly composed of white matter (except the grey kernels). For simplicity reasons, we consider in the model that brain cortex only contains grey matter and brain medium only contains white matter. The ionic species considered in this model are $K^{+}$, $N{a}^{+}$, $C{l}^{-}$, $C{a}^{2+}$ and the Glutamate ($glu$). They pass through neuronal and glial membranes via ionic channels and via ionic pumps and transporters. Altogether, the mean field model has 19 unknowns and is of reaction-diffusion type, except that there is no diffusion for 4 unknowns. There is also a difference in the number of reaction-diffusion equations in grey matter and in white matter. Since grey matter contains astrocytes (which are linked into an astrocytic synticium thanks to gap-junctions), ions are able to diffuse in the astrocytic space as well as in the extracellular space in grey matter. On the contrary, as the main glial cells in white matter are oligodendrocytes, ions are considered to be only able to diffuse in extracellular space in white matter. As a consequence, the model contains 10 reaction-diffusion equations in grey matter (for the concentrations of K+, Na+, Ca2+, Cl- and Glu in astrocytes and in the extracellular space) and 5 reaction-diffusion equations in white matter (for the concentrations of K+, Na+, Ca2+, Cl- and glu in the extracellular space). The domain corresponds to a human brain and is divided in grey and white matter. These two matters differ in several coefficients in the reaction term (corresponding to the cell composition) and in their diffusion coefficients. To run this model on such a complex geometry, we had to develop new numerical methods. A first description of the algorithms used for the numerical solution of this stroke model on 1D and 2D geometries was presented in a previous article (Descombes and Dumont, 2008). However, since we need to take into account the anatomic and histological specificities of human brain, this model needs to run on a 3D realistic geometry, which implies to develop powerful numerical methods able to deal with a broad spectrum of spatial and temporal scales. The numerical method is based on operator splitting and explicit/implicit Runge-Kutta methods. We then show, for the first time, numerical simulations in 3D obtained thanks to a particular implementation of parallelism, in the framework of shared memory machines. The simulation results show spreading depressions which propagate exclusively in grey matter, which was expected. We then studied the evolution of the extracellular concentration of potassium and of the rADCw (which reflect the severity of ischemia) in the domain. The quantitative values obtained for these two biomarkers in the infarcted core and in the surroundings are consistent with the values measured during biological experiments or with medical imaging.

Model of cell death

Studying the relationships between necrosis and apoptosis in stroke with simulations is of the most importance since they are difficult to study with in vitro or in vivo experiments. Moreover, this question is currently important since new anti-apoptotic strategies are currently under study in stroke patients (such as the CsA). This model is currently a qualitative model and can't be validated with quantitative data yet. But we plan to use perfusion images and diffusion images to have some "input" situations and some "output" situations of the damage extension. We are currently discussing these questions with physicians in the neurologic unit in Lyon hospital.

Inflammation

These models are important to continue and to develop since the role of the inflammatory process in stroke needs to be better understood. We need to use and to obtain new quantitative data from in vivo experiments (biological dosages or medical imaging) to improve the parametrisation of the models (the ODE and the PDE models) and their validation. That's why we need to continue working with biologists and scientists working on medical images (such as in CREATIS in Lyon).

Free radicals

The model gives first interesting results but it needs to be developed. We will continue working on this model with data coming from Michel Plotkine and Isabelle Margaill (EA 2510, pharmacie, Paris 5). An M2 master student will be supervised in 2013-2014 on this subject. These data should help to complete the parametrisation of the model and to validate the model.

Spreading depressions

The study of spreading depressions in stroke has been an important subject of the "AVC-in silico" team but our current models are not focused on this mechanism. However, the numerical methods developed during these studies are currently used in other models such as in models of inflammation (which contain reaction-diffusion equations and also equations of chemotaxis).

Collaborations

• Chapuisat Guillemette (LATP, UMR CNRS 6632, Université Aix-Marseille 3)

• Di Russo Cristiana (MAPMO, UMR CNRS 7349, Université d'Orléans)

• De Simoni Maria Grazia (Neurosciences, Mario Negri Institute, Milan, Italy)

• Berthezène Yves, Wiart Marlene, Rousseau David (neurologic unit, Lyon hospital and CREATIS, CNRS UMR 5220 - INSERM U1044 - Université Lyon 1 - INSA Lyon)

• Plotkine Michel and Margaill Isabelle (EA 2510, pharmacie, Paris 5)

• Lemesle Valèrie (Montpelliers)

• Descombes Stṕhane (Laboratoire J.A Dieudonné, UMR CNRS 7351)