Section: New Results

Hexahedral-dominant Remeshing

Participants : Dmitry Sokolov, Nicolas Ray, Bruno Lévy, Maxence Reberol.

Representing the geometry of complex objects in a computer is usually achieved by a mesh: the object is decomposed in cells that have a simple geometry. Each cell is defined by a set of facets. The simplest choice is to use meshes with tetrahedral cells that are relatively easy to produce and to work with. However, some applications involving numerical simulations better work with hexahedral cells. Such hexahedral meshes are very difficult to produce, even when it is completely done by a designer.

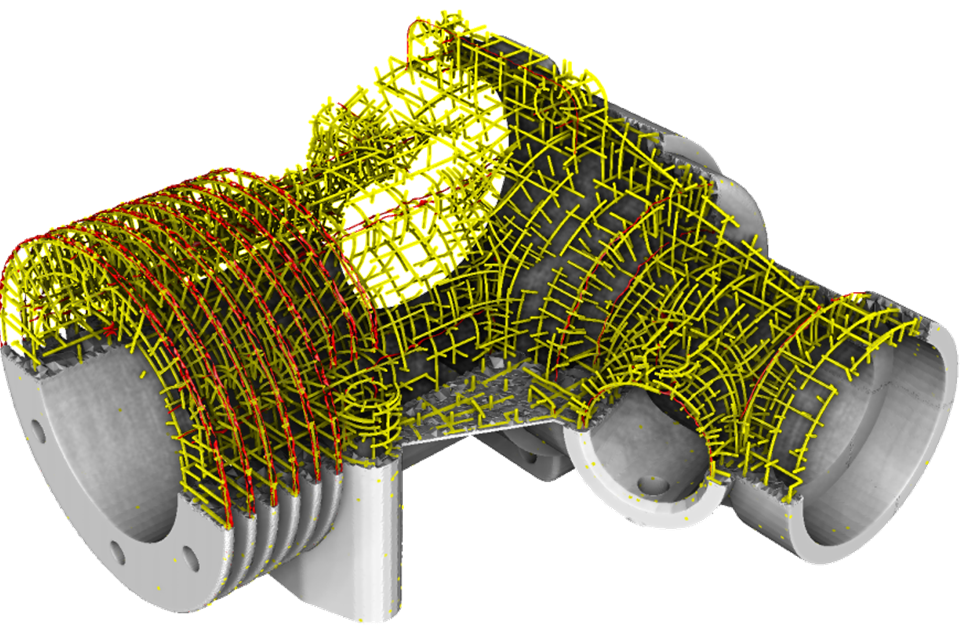
Our objective is to relax the intrinsic difficulties of full hexahedral remeshing by allowing the process to generate a few tetrahedra in the hexahedral mesh (hexahedral-dominant meshes). Our approach is a two steps procedure that defines the desired orientation of the hexahedra with a frame field, then integrates this frame field to generate a deformed 3D grid inside the object. Hexahedra are generated where the grid is non degenerated and not too distorted, and tetrahedra will fill the remaining volume.

Frame Field Generation

A frame field must define the orientation of a cube (the less deformed hexahedron) everywhere inside the object. This object is very difficult to manipulate because it has to be invariant by rotation of 90 degrees around each of its facet normal vector. In [26] we have designed a fast algorithm that is able to define a smooth frame field constrained to be aligned with the object boundary. We represent frames by spherical harmonics (as introduced in [33] ) and greatly improve the state of the art thanks to an expression of the boundary constraints that keep the objective function of the optimisation problem very close to quadratic.

Generation of Hexahedral-dominant Meshes

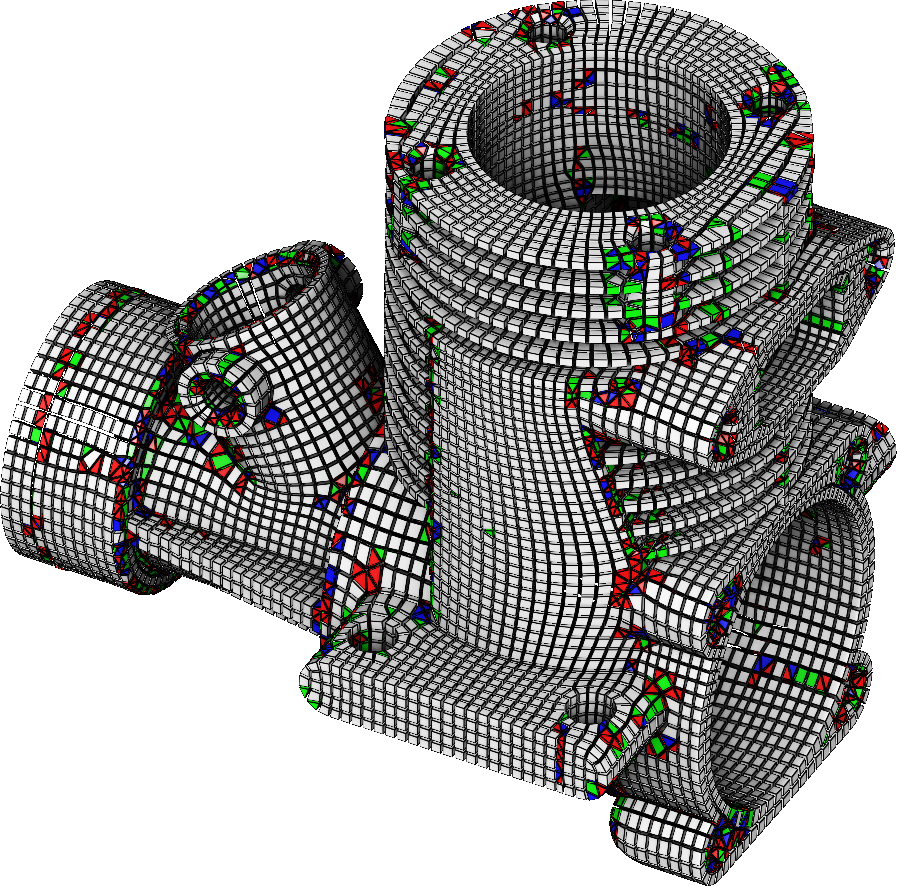
The generation of the hex dominant meshes is performed in two steps: place a deformed 3D grid inside the object such that it is aligned with the frame field, then use it to produce hexahedra and fill the rest of the volume with tetrahedra. We developed two solutions for the first step: a 3D extension of PGP [40] and an adaptation of Cubecover [39] . Both solutions have pros and cons so we plan to make them cooperate in a near future. The conversion of this result in an hexahedral-dominant mesh is a very complex problem for which we have a fair solution: we extract a point set from the deformed 3D grid, generate a tetrahedral mesh of the object that is constrained to include the point set in its vertices. From this tetrahedral mesh, we merge sets of tetrahedra into hexahedra with an extension of [37] . We are now working on an alternative solution that will generate hexahedra directly from the deformed 3D grid, and extract the boundary of the rest of the volume as a 2D mesh. From this mesh, we will try to produce more hexahedra by adapting existing combinatorial methods [27] .

Impact on FEM Performance

It is admitted by our scientific community that hexahedral meshes are better than tetrahedral meshes for some FEM simulation. We would like to demonstrate evidence of this belief, including fair comparisons with equal running time and/or result accuracy, but the best function basis for each case. For hexahedral dominant meshes, we want to determine if the benefit of using hexahedra deserves having specific function bases devoted to properly link tetrahedral and hexahedral elements. We are developing a new function basis, tailored to non-conformal mixed hexahedra-tetrahedra meshes. Using a combination of tri-linear and quadratic hexahedra, it is possible to construct a space of continuous functions even on a non-conformal mesh. We are now proceeding to analyse the properties of this function space, both theoretically and experimentally. This topic is addressed in the (ongoing) Ph.D. thesis of Maxence Reberol.