Section: New Results
Electrostrictive materials: modelling and simulation
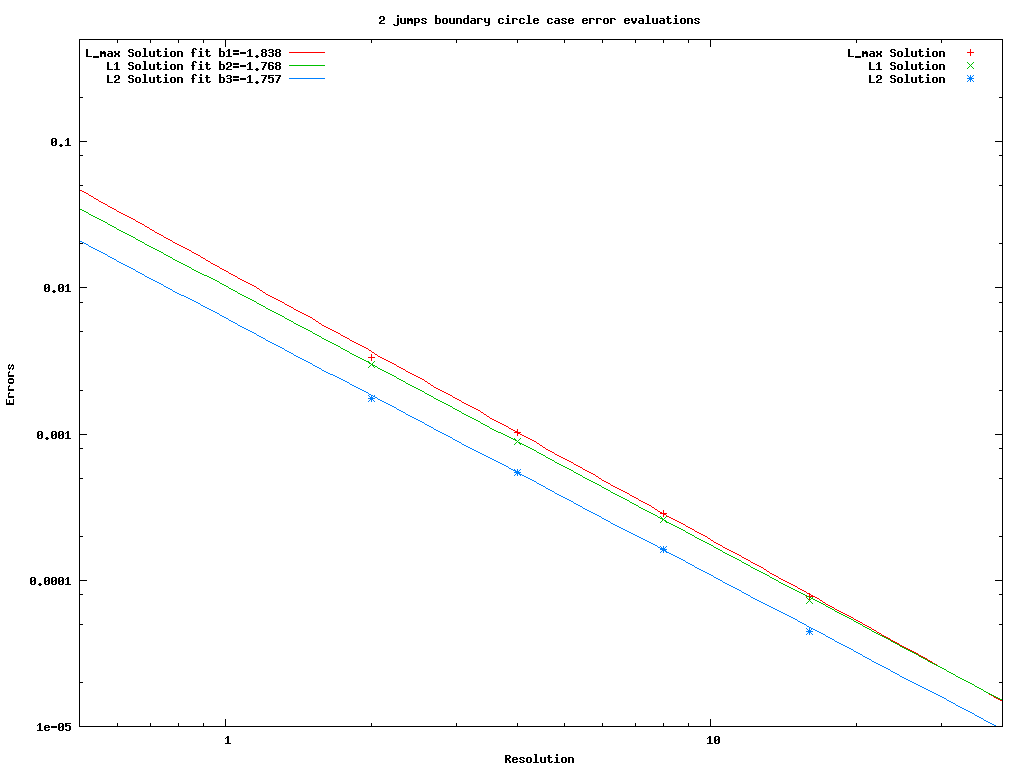
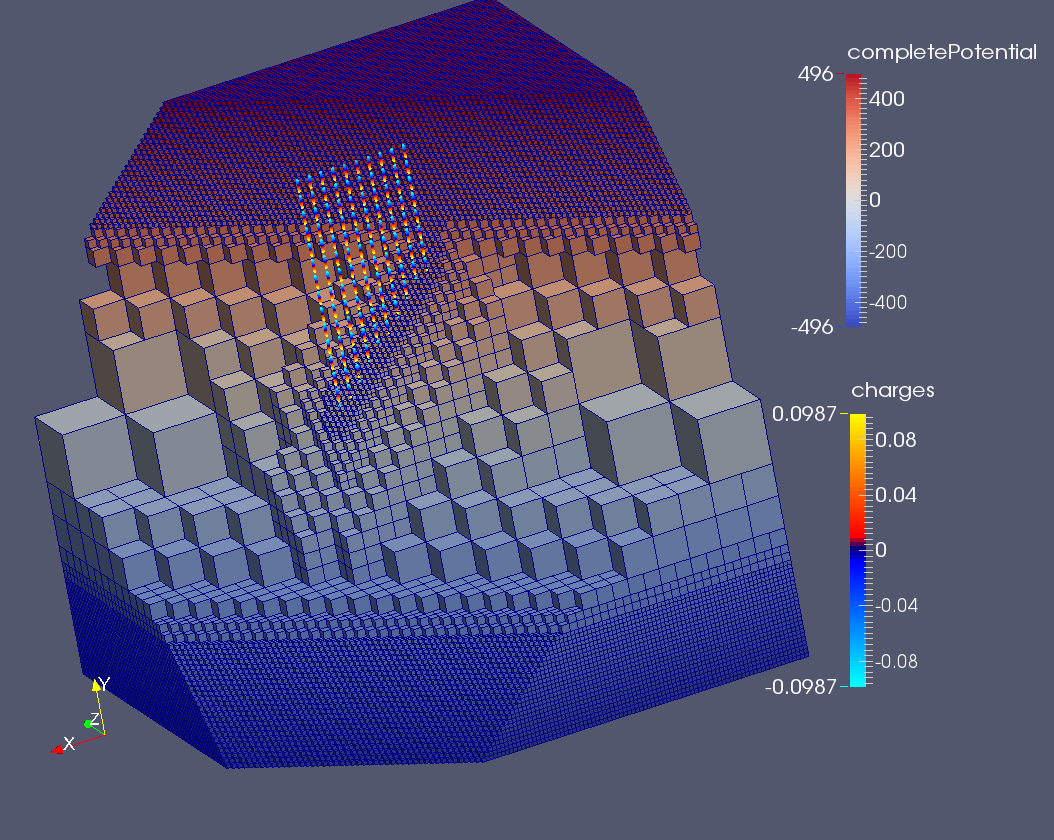
In this work, a result of the collaboration between physicists, chemists (Annie Colin and Philippe Poulin, CRPP Bordeaux) and applied mathematicians, we deal with mathematical modelling and simulation of electrostrictive materials. These kinds of materials are composed by a polymeric matrix with carbon nanotubes embedded in and this structure gives them interesting electrical properties. Their dielectric constant varies as a function of the mechanical deformation. Housed in a capacitor, they show variable capacity when subjected to vibration and they can generate potential differences from mechanical deformations. Because of their composition, their structure involves different physical scales, from the small nanotube dimension, through the scale of nanotube clusters, to the large dimension of the sample. Our purpose is to provide physicists and chemists with a tool to test in silico several material configurations and to have a deeper insight into the features of these materials, developing numerical models which can predict their steady and unsteady behaviour. We propose to model the physical problem by reducing the nanotubes to dipoles and solving a Gauss equation for the electrical potential equation informed of the presence of nanotubes with zero electrical field conditions on the centres of the nanotubes. We started considering the steady problem, which is interesting for the purpose of understanding the basic electrical properties of different nanotube configurations and of designing of the material. In order to discretize and simulate the mathematical problem, we chose parallel linear octree-based adaptive meshes and we developed an original hybrid Finite Volume/Finite Difference second-order scheme for 2D and 3D elliptic problems on this kind of mesh. A convergence analysis of the numerical scheme has been developed and validating test cases have been performed. Good qualitative agreement between numerical and real experiments has been observed for the steady model. In the future we aim to quantitatively compare the numerical results and the real material behaviour, to model the unsteady problem and to deal with electrical consequences of mechanical deformations.