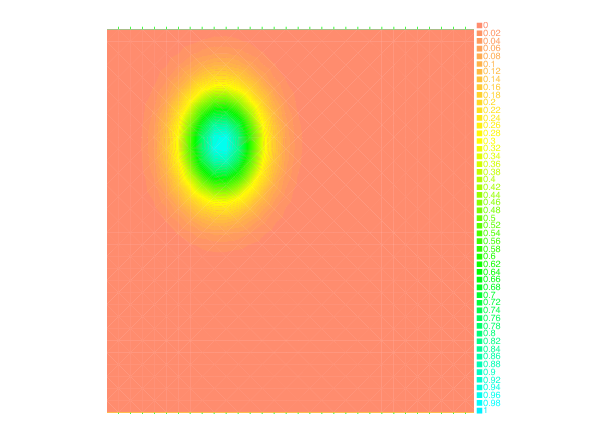
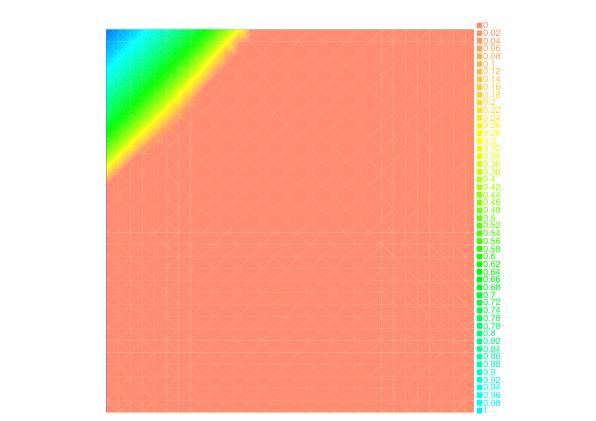
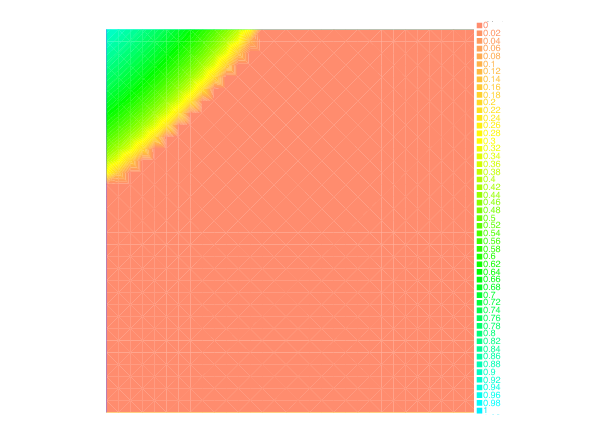
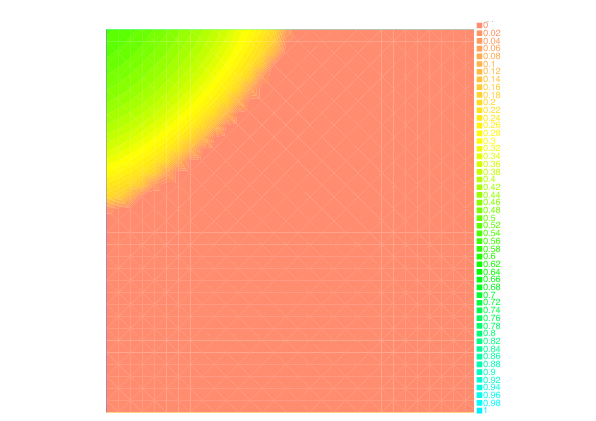
Section: New Results
Numerical methods for JKO Gradient Flows
J-D. Benamou, G. Carlier, M. Laborde, G. Peyré, B. Schmitzer, V. Duval
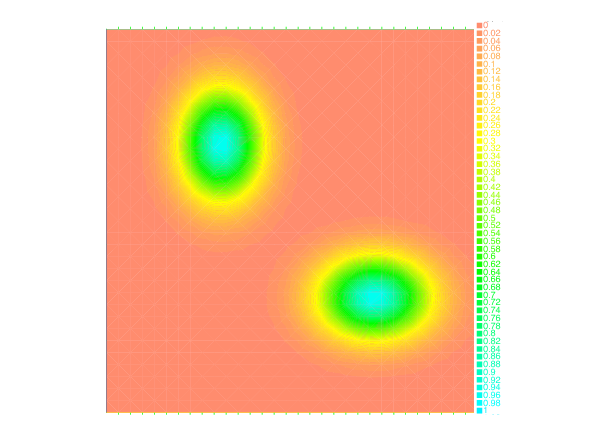
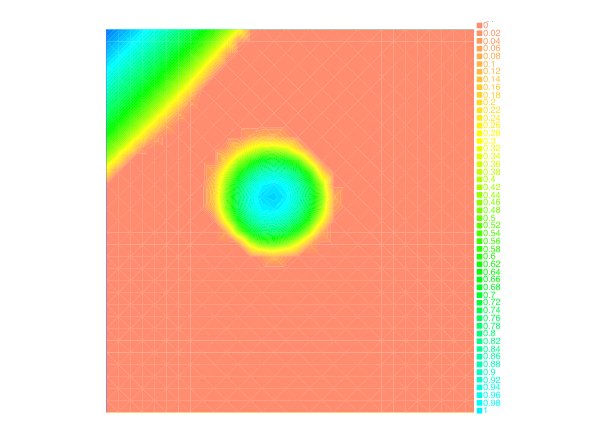
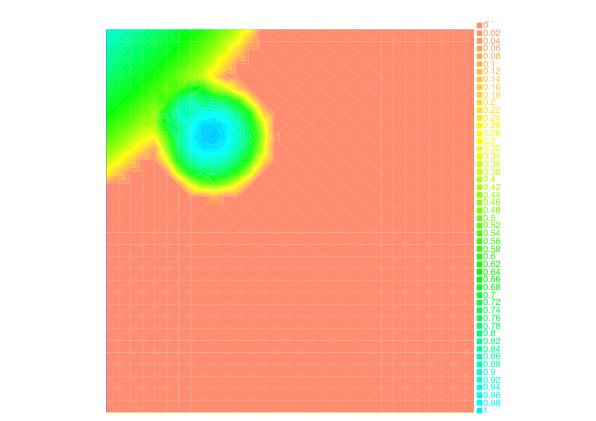
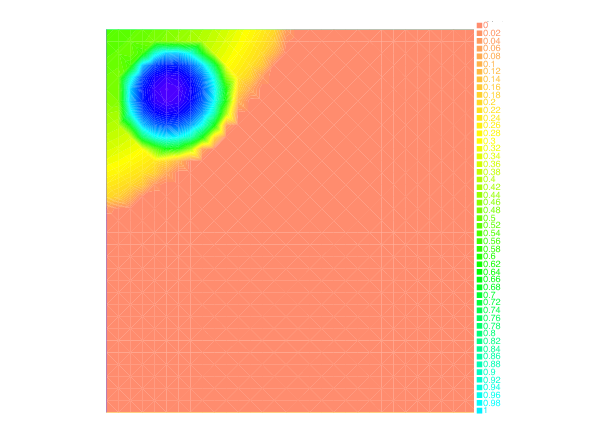
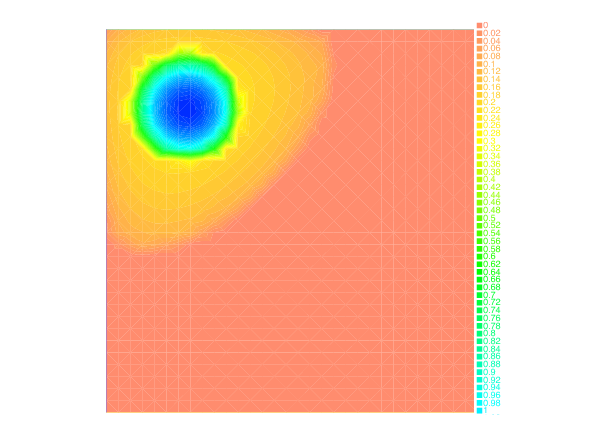
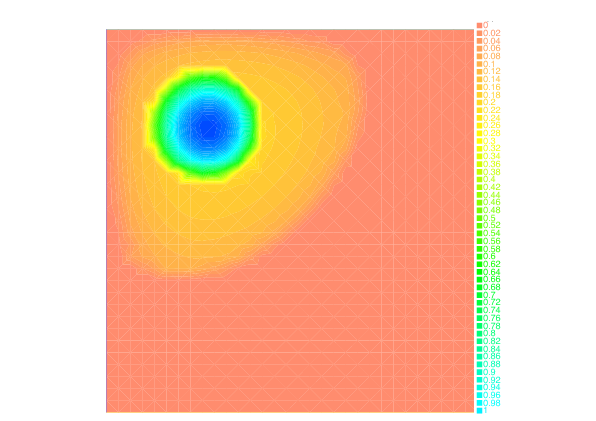
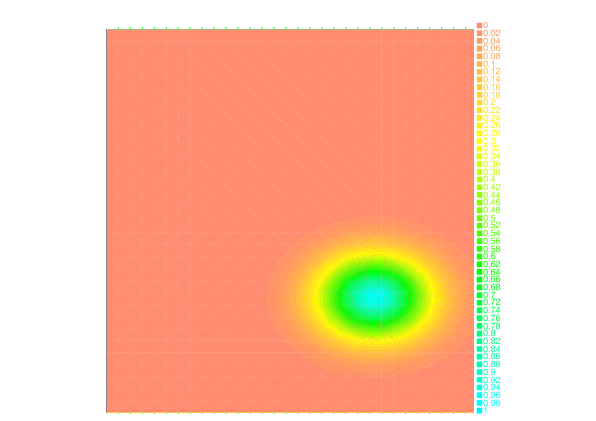
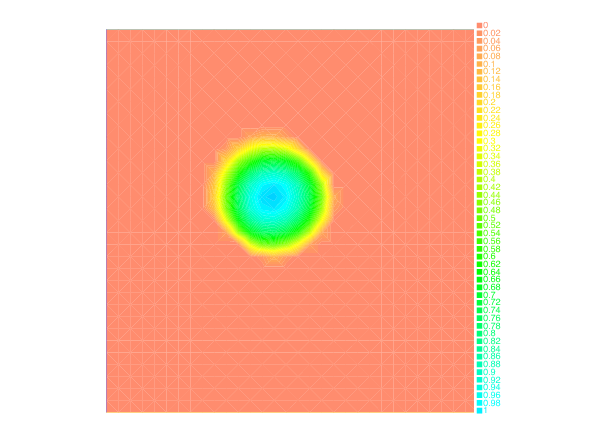
Taking advantage of the Benamou-Brenier dynamic formulation of optimal transport, we propose in [28] , a convex formulation for each step of the JKO scheme for Wasserstein gradient flows which can be attacked by an augmented Lagrangian method which we call the ALG2-JKO scheme. We test the algorithm in particular on the porous medium equation. We also consider a semi implicit variant which enables us to treat nonlocal interactions as well as systems of interacting species. Regarding systems, we can also use the ALG2-JKO scheme for the simulation of crowd motion models with several species.
|
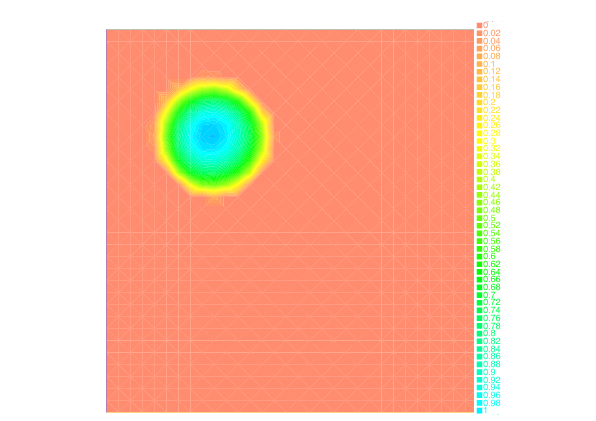
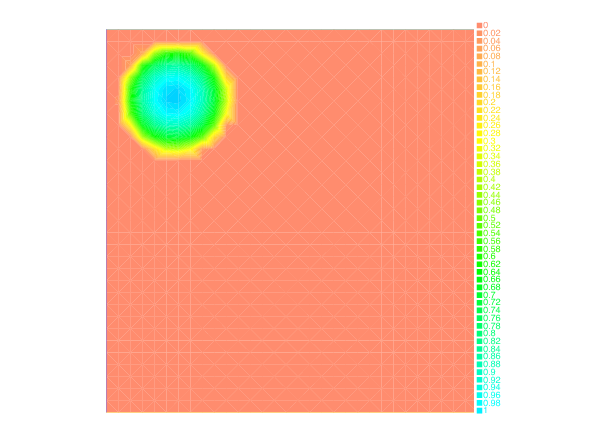
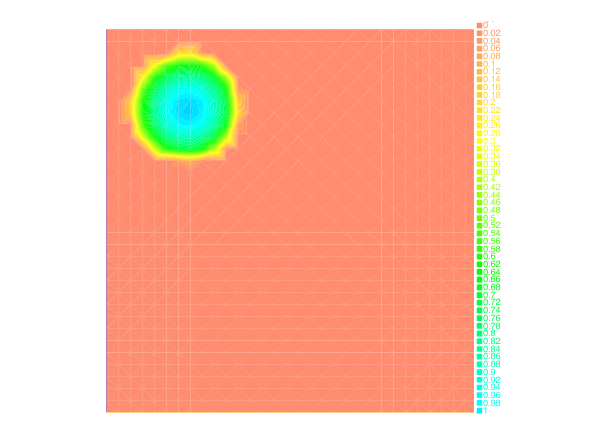
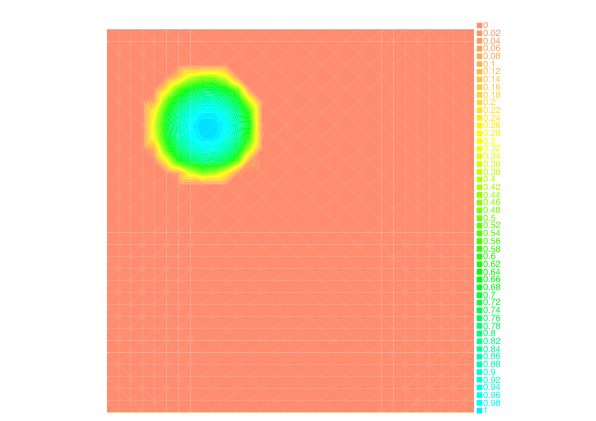
We have also investigated the entropy-regularization of the Wasserstein metric to compute gradient flows [19] , [34] . This entropic regularization trades the usual Wasserstein fidelity term for a Kullback-Leibler divergence term. Adapting first-order proximal methods to this framework, we have developed numerical schemes which dramatically reduce the computational load needed to simulate the evolution of a mass density through a JKO flow. By construction, the entropy regularization yields an additional diffusion effects to the evolution, but we have proved that a careful choice of the regularization parameter with respect to the timestep yields the convergence of the scheme towards the solutions of the continuous PDE.
A novel Lagrangian method using a discretization of the Monge-Ampère operator for JKO has been developed in [13] . Not only convergence of the scheme has been established but also one advantage of this method is that it makes it possible to use a Newton's method .