Section: New Results
Phase estimation in Differential Interference Contrast (DIC) microscopy
Participants : Lola-Xiomara Bautista Rozo, Laure Blanc-Féraud.
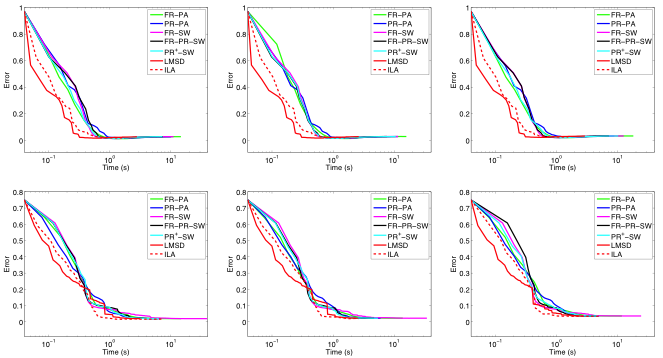
We address the problem of estimating the phase from color images acquired with differential-interference-contrast microscopy. In particular, we consider the nonlinear and nonconvex optimization problem obtained by regularizing a least-squares-like discrepancy term with a total variation functional, possibly smoothed with the introduction of a positive constant. We deeply investigate the analytic properties of the resulting objective function, proving the existence of minimum points, and several optimization methods able to address the minimization problem. Besides revisiting the conjugate gradient method proposed in the literature for this problem and comparing it with standard conjugate gradient approaches, we introduce more recent effective optimization tools able to obtain both in the smooth and in the non smooth case accurate reconstructions with a reduced computational demand.
|