Keywords
Computer Science and Digital Science
- A2.5. Software engineering
- A3.3.2. Data mining
- A3.4.1. Supervised learning
- A3.4.2. Unsupervised learning
- A6.1.4. Multiscale modeling
- A6.2.4. Statistical methods
- A6.2.8. Computational geometry and meshes
- A8.1. Discrete mathematics, combinatorics
- A8.3. Geometry, Topology
- A8.7. Graph theory
- A9.2. Machine learning
Other Research Topics and Application Domains
- B1.1.1. Structural biology
- B1.1.5. Immunology
- B1.1.7. Bioinformatics
1 Team members, visitors, external collaborators
Research Scientists
- Frédéric Cazals [Team leader, Inria, Senior Researcher, HDR]
- Dorian Mazauric [Inria, Researcher]
PhD Students
- Timothee O Donnell [Inria]
- Meline Simsir [Univ Côte d'Azur, until Nov 2020]
Interns and Apprentices
- Stephane Bereux [Inria, from Apr 2020 until Aug 2020]
- Gregoire Francisco [Inria, from May 2020 until Sep 2020]
- Valentin Madelaine [Inria, from Oct 2020]
- Augusto Sales De Queiroz [Univ Côte d'Azur, from Mar 2020 until Jul 2020]
Administrative Assistant
- Florence Barbara [Inria]
Visiting Scientist
- Thiziri Nait Saada [Telecom ParisTech, until Jun 2020]
External Collaborators
- Charles Robert [CNRS, HDR]
- Konstantin Roeder [Robinson College - Cambridge, from Feb 2020]
2 Overall objectives
Computational Biology and Computational Structural Biology. Understanding the lineage between species and the genetic drift of genes and genomes, apprehending the control and feed-back loops governing the behavior of a cell, a tissue, an organ or a body, and inferring the relationship between the structure of biological (macro)-molecules and their functions are amongst the major challenges of modern biology. The investigation of these challenges is supported by three types of data: genomic data, transcription and expression data, and structural data.
Genetic data feature sequences of nucleotides on DNA and RNA molecules, and are symbolic data whose processing falls in the realm of Theoretical Computer Science: dynamic programming, algorithms on texts and strings, graph theory dedicated to phylogenetic problems. Transcription and expression data feature evolving concentrations of molecules (RNAs, proteins, metabolites) over time, and fit in the formalism of discrete and continuous dynamical systems, and of graph theory. The exploration and the modeling of these data are covered by a rapidly expanding research field termed systems biology. Structural data encode informations about the 3D structures of molecules (nucleic acids (DNA, RNA), proteins, small molecules) and their interactions, and come from three main sources: X ray crystallography, NMR spectroscopy, cryo Electron Microscopy. Ultimately, structural data should expand our understanding of how the structure accounts for the function of macro-molecules – one of the central questions in structural biology. This goal actually subsumes two equally difficult challenges, which are folding – the process through which a protein adopts its 3D structure, and docking – the process through which two or several molecules assemble. Folding and docking are driven by non covalent interactions, and for complex systems, are actually inter-twined 47. Apart from the bio-physical interests raised by these processes, two different application domains are concerned: in fundamental biology, one is primarily interested in understanding the machinery of the cell; in medicine, applications to drug design are developed.
Modeling in Computational Structural Biology. Acquiring structural data is not always possible: NMR is restricted to relatively small molecules; membrane proteins do not crystallize, etc. As a matter of fact, the order of magnitude of the number of genomes sequenced is of the order of one thousand, which results in circa one million of genes recorded in the manually curated Swiss-Prot database. On the other hand, the Protein Data Bank contains circa 90,000 structures. Thus, the paucity of structures with respect to the known number of genes calls for modeling in structural biology, so as to foster our understanding of the structure-to-function relationship.
Ideally, bio-physical models of macro-molecules should resort to quantum mechanics. While this is possible for small systems, say up to 50 atoms, large systems are investigated within the framework of the Born-Oppenheimer approximation which stipulates the nuclei and the electron cloud can be decoupled. Example force fields developed in this realm are AMBER, CHARMM, OPLS. Of particular importance are Van der Waals models, where each atom is modeled by a sphere whose radius depends on the atom chemical type. From an historical perspective, Richards 45, 34 and later Connolly 30, while defining molecular surfaces and developing algorithms to compute them, established the connexions between molecular modeling and geometric constructions. Remarkably, a number of difficult problems (e.g. additively weighted Voronoi diagrams) were touched upon in these early days.
The models developed in this vein are instrumental in investigating the interactions of molecules for which no structural data is available. But such models often fall short from providing complete answers, which we illustrate with the folding problem. On one hand, as the conformations of side-chains belong to discrete sets (the so-called rotamers or rotational isomers) 36, the number of distinct conformations of a poly-peptidic chain is exponential in the number of amino-acids. On the other hand, Nature folds proteins within time scales ranging from milliseconds to hours, while time-steps used in molecular dynamics simulations are of the order of the femto-second, so that biologically relevant time-scales are out reach for simulations. The fact that Nature avoids the exponential trap is known as Levinthal's paradox. The intrinsic difficulty of problems calls for models exploiting several classes of informations. For small systems, ab initio models can be built from first principles. But for more complex systems, homology or template-based models integrating a variable amount of knowledge acquired on similar systems are resorted to.
The variety of approaches developed are illustrated by the two
community wide experiments CASP (Critical Assessment of Techniques
for Protein Structure Prediction; https://
As illustrated by the previous discussion, modeling macro-molecules touches upon biology, physics and chemistry, as well as mathematics and computer science. In the following, we present the topics investigated within ABS.
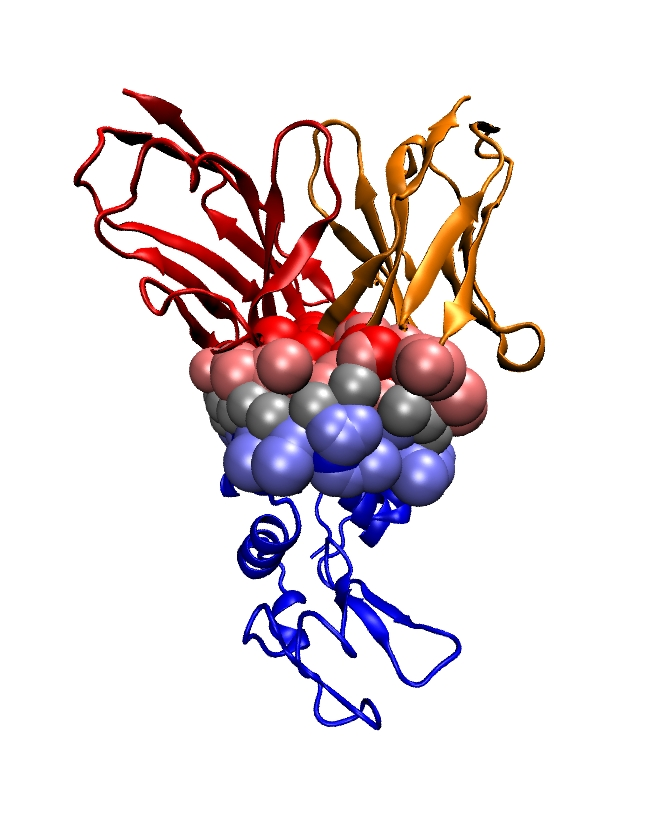
|
|
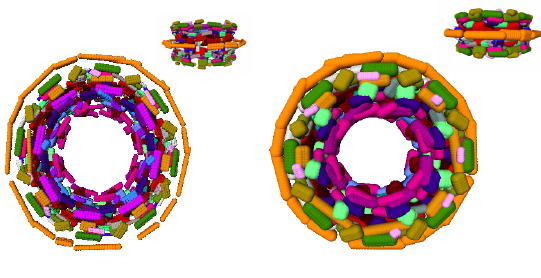
|
| (a) | (b) | (c) |
3 Research program
The research conducted by ABS focuses on three main directions in Computational Structural Biology (CSB), together with the associated methodological developments:
– Modeling interfaces and contacts,
– Modeling macro-molecular assemblies,
– Modeling the flexibility of macro-molecules,
– Algorithmic foundations.
3.1 Modeling interfaces and contacts
Keywords: Docking, interfaces, protein complexes, structural alphabets, scoring functions, Voronoi diagrams, arrangements of balls.
The Protein Data Bank, http://
The description of interfaces is also of special interest to improve scoring functions. By scoring function, two things are meant: either a function which assigns to a complex a quantity homogeneous to a free energy change 2, or a function stating that a complex is more stable than another one, in which case the value returned is a score and not an energy. Borrowing to statistical mechanics 28, the usual way to design scoring functions is to mimic the so-called potentials of mean force. To put it briefly, one reverts Boltzmann's law, that is, denoting the probability of two atoms –defining type – to be located at distance , the (free) energy assigned to the pair is computed as . Estimating from the PDB one function for each type of pair of atoms, the energy of a complex is computed as the sum of the energies of the pairs located within a distance threshold 48, 35. To compare the energy thus obtained to a reference state, one may compute , with the observed frequencies, and the frequencies stemming from an a priori model 40. In doing so, the energy defined is nothing but the Kullback-Leibler divergence between the distributions and .
Describing interfaces poses problems in two settings: static and dynamic.
In the static setting, one seeks the minimalist geometric model providing a relevant bio-physical signal. A first step in doing so consists of identifying interface atoms, so as to relate the geometry and the bio-chemistry at the interface level 12. To elaborate at the atomic level, one seeks a structural alphabet encoding the spatial structure of proteins. At the side-chain and backbone level, an example of such alphabet is that of 29. At the atomic level and in spite of recent observations on the local structure of the neighborhood of a given atom 49, no such alphabet is known. Specific important local conformations are known, though. One of them is the so-called dehydron structure, which is an under-desolvated hydrogen bond – a property that can be directly inferred from the spatial configuration of the carbons surrounding a hydrogen bond 32.
In the dynamic setting, one wishes to understand whether selected (hot) residues exhibit specific dynamic properties, so as to serve as anchors in a binding process 43. More generally, any significant observation raised in the static setting deserves investigations in the dynamic setting, so as to assess its stability. Such questions are also related to the problem of correlated motions, which we discuss next.
3.2 Modeling macro-molecular assemblies
Keywords: Macro-molecular assembly, reconstruction by data integration, proteomics, modeling with uncertainties, curved Voronoi diagrams, topological persistence.
3.2.1 Reconstruction by Data Integration
Large protein assemblies such as the Nuclear Pore Complex (NPC), chaperonin cavities, the proteasome or ATP synthases, to name a few, are key to numerous biological functions. To improve our understanding of these functions, one would ideally like to build and animate atomic models of these molecular machines. However, this task is especially tough, due to their size and their plasticity, but also due to the flexibility of the proteins involved. In a sense, the modeling challenges arising in this context are different from those faced for binary docking, and also from those encountered for intermediate size complexes which are often amenable to a processing mixing (cryo-EM) image analysis and classical docking. To face these new challenges, an emerging paradigm is that of reconstruction by data integration 27. In a nutshell, the strategy is reminiscent from NMR and consists of mixing experimental data from a variety of sources, so as to find out the model(s) best complying with the data. This strategy has been in particular used to propose plausible models of the Nuclear Pore Complex 26, the largest assembly known to date in the eukaryotic cell, and consisting of 456 protein instances of 30 types.
3.2.2 Modeling with Uncertainties and Model Assessment
Reconstruction by data integration requires three ingredients. First, a parametrized model must be adopted, typically a collection of balls to model a protein with pseudo-atoms. Second, as in NMR, a functional measuring the agreement between a model and the data must be chosen. In 25, this functional is based upon restraints, namely penalties associated to the experimental data. Third, an optimization scheme must be selected. The design of restraints is notoriously challenging, due to the ambiguous nature and/or the noise level of the data. For example, Tandem Affinity Purification (TAP) gives access to a pullout i.e. a list of protein types which are known to interact with one tagged protein type, but no information on the number of complexes or on the stoichiometry of proteins types within a complex is provided. In cryo-EM, the envelope enclosing an assembly is often imprecisely defined, in particular in regions of low density. For immuno-EM labelling experiments, positional uncertainties arise from the microscope resolution.
These uncertainties coupled with the complexity of the functional being optimized, which in general is non convex, have two consequences. First, it is impossible to single out a unique reconstruction, and a set of plausible reconstructions must be considered. As an example, 1000 plausible models of the NPC were reported in 25. Interestingly, averaging the positions of all balls of a particular protein type across these models resulted in 30 so-called probability density maps, each such map encoding the probability of presence of a particular protein type at a particular location in the NPC. Second, the assessment of all models (individual and averaged) is non trivial. In particular, the lack of straightforward statistical analysis of the individual models and the absence of assessment for the averaged models are detrimental to the mechanistic exploitation of the reconstruction results. At this stage, such models therefore remain qualitative.
3.3 Modeling the flexibility of macro-molecules
Keywords: Folding, docking, energy landscapes, induced fit, molecular dynamics, conformers, conformer ensembles, point clouds, reconstruction, shape learning, Morse theory.
Proteins in vivo vibrate at various frequencies: high frequencies correspond to small amplitude deformations of chemical bonds, while low frequencies characterize more global deformations. This flexibility contributes to the entropy thus the free energy of the system protein - solvent. From the experimental standpoint, NMR studies generate ensembles of conformations, called conformers, and so do molecular dynamics (MD) simulations. Of particular interest while investigating flexibility is the notion of correlated motion. Intuitively, when a protein is folded, all atomic movements must be correlated, a constraint which gets alleviated when the protein unfolds since the steric constraints get relaxed 3. Understanding correlations is of special interest to predict the folding pathway that leads a protein towards its native state. A similar discussion holds for the case of partners within a complex, for example in the third step of the diffusion - conformer selection - induced fit complex formation model.
Parameterizing these correlated motions, describing the corresponding energy landscapes, as well as handling collections of conformations pose challenging algorithmic problems.
At the side-chain level, the question of improving rotamer libraries is still of interest 31. This question is essentially a clustering problem in the parameter space describing the side-chains conformations.
At the atomic level, flexibility is essentially investigated resorting to methods based on a classical potential energy (molecular dynamics), and (inverse) kinematics. A molecular dynamics simulation provides a point cloud sampling the conformational landscape of the molecular system investigated, as each step in the simulation corresponds to one point in the parameter space describing the system (the conformational space) 46. The standard methodology to analyze such a point cloud consists of resorting to normal modes. Recently, though, more elaborate methods resorting to more local analysis 42, to Morse theory 37 and to analysis of meta-stable states of time series 38 have been proposed.
3.4 Algorithmic foundations
Keywords: Computational geometry, computational topology, optimization, data analysis.
Making a stride towards a better understanding of the biophysical questions discussed in the previous sections requires various methodological developments, which we briefly discuss now.
Modeling Interfaces and Contacts
In modeling interfaces and contacts, one may favor geometric or topological information.
On the geometric side, the problem of modeling contacts at the atomic level is tantamount to encoding multi-body relations between an atom and its neighbors. On the one hand, one may use an encoding of neighborhoods based on geometric constructions such as Voronoi diagrams (affine or curved) or arrangements of balls. On the other hand, one may resort to clustering strategies in higher dimensional spaces, as the neighbors of a given atom are represented by degrees of freedom – the neighborhood being invariant upon rigid motions. The information gathered while modeling contacts can further be integrated into interface models.
On the topological side, one may favor constructions which remain stable if each atom in a structure retains the same neighbors, even though the 3D positions of these neighbors change to some extent. This process is observed in flexible docking cases, and call for the development of methods to encode and compare shapes undergoing tame geometric deformations.
Modeling Macro-molecular Assemblies
In dealing with large assemblies, a number of methodological developments are called for.
On the experimental side, of particular interest is the disambiguation of proteomics signals. For example, TAP and mass spectrometry data call for the development of combinatorial algorithms aiming at unraveling pairwise contacts between proteins within an assembly. Likewise, density maps coming from electron microscopy, which are often of intermediate resolution (5-10Å) call the development of noise resilient segmentation and interpretation algorithms. The results produced by such algorithms can further be used to guide the docking of high resolutions crystal structures into maps.
As for modeling, two classes of developments are particularly stimulating. The first one is concerned with the design of algorithms performing reconstruction by data integration, a process reminiscent from non convex optimization. The second one encompasses assessment methods, in order to single out the reconstructions which best comply with the experimental data. For that endeavor, the development of geometric and topological models accommodating uncertainties is particularly important.
Modeling the Flexibility of Macro-molecules
Given a sampling on an energy landscape, a number of fundamental issues actually arise: how does the point cloud describe the topography of the energy landscape (a question reminiscent from Morse theory)? Can one infer the effective number of degrees of freedom of the system over the simulation, and is this number varying? Answers to these questions would be of major interest to refine our understanding of folding and docking, with applications to the prediction of structural properties. It should be noted in passing that such questions are probably related to modeling phase transitions in statistical physics where geometric and topological methods are being used 41.
From an algorithmic standpoint, such questions are reminiscent of shape learning. Given a collection of samples on an (unknown) model, learning consists of guessing the model from the samples – the result of this process may be called the reconstruction. In doing so, two types of guarantees are sought: topologically speaking, the reconstruction and the model should (ideally!) be isotopic; geometrically speaking, their Hausdorff distance should be small. Motivated by applications in Computer Aided Geometric Design, surface reconstruction triggered a major activity in the Computational Geometry community over the past ten years. Aside from applications, reconstruction raises a number of deep issues: the study of distance functions to the model and to the samples, and their comparison; the study of Morse-like constructions stemming from distance functions to points; the analysis of topological invariants of the model and the samples, and their comparison.
4 Application domains
The main application domain is Computational Structural Biology, as developed in the Research Program.
5 Highlights of the year
The ultimate goal of ABS is to propose tools fostering our understanding of the relationship between the structure, dynamics and function of biomolecular machines. In this respect, the new results of the year make a steady progress, providing complementary tools. On the structural side and the static analysis of biomolecular structures, we have shown on a very complex system, namely the efflux pump AcrB 24, that database driven approaches could reveal subtle properties, when analyzed with the appropriate geometric and clustering tools. On the dynamics side, we have achieved significant milestones. Our improved Wang-Landau algorithm 22 indeed paves to way to efficient methods to compute densities of states (and therefore thermodynamic properties).
Moreover, all these tools have been incorporated into the release of the Structural Bioinformatics Library.
6 New software and platforms
6.1 New software
6.1.1 SBL
- Name: Structural Bioinformatics Library
- Keywords: Structural Biology, Biophysics, Software architecture
-
Functional Description:
The SBL is a generic C++/python cross-platform software library targeting complex problems in structural bioinformatics. Its tenet is based on a modular design offering a rich and versatile framework allowing the development of novel applications requiring well specified complex operations, without compromising robustness and performances.
More specifically, the SBL involves four software components (1-4 thereafter). For end-users, the SBL provides ready to use, state-of-the-art (1) applications to handle molecular models defined by unions of balls, to deal with molecular flexibility, to model macro-molecular assemblies. These applications can also be combined to tackle integrated analysis problems. For developers, the SBL provides a broad C++ toolbox with modular design, involving core (2) algorithms, (3) biophysical models, and (4) modules, the latter being especially suited to develop novel applications. The SBL comes with a thorough documentation consisting of user and reference manuals, and a bugzilla platform to handle community feedback.
- Release Contributions: In 2020, four new packages have been released. Two of them belong to the Applications group: molecular cradle, to study the relative motions of subunits in large molecular machines, and multiple interface string alignments, to compare the interfaces of protein complexes involving similar molecules. Two of them belong to the core of the library: Wang-Landau proposes a generic implementation of the eponym algorithm, while Hamiltonian Monte Carlo (HMC) makes available a robust implementation of HMC, with applications to the computation of the volume of high dimensional polytopes.
-
URL:
https://
sbl. inria. fr/ - Publication: hal-01570848
- Contact: Frédéric Cazals
7 New results
7.1 Modeling interfaces and contacts
Keywords: docking, scoring, interfaces, protein complexes, Voronoi diagrams, arrangements of balls.
7.1.1 Comparing interfaces in protein complexes
Participant: F. Cazals.
In collaboration with S. Bereux (Ecole Polytechnique), and B. Delmas (INRAe, Jouy-en-Josas).
We introduce Multiple Interface String Alignment (MISA) 20, a visualization tool to display coherently various sequence and structure based statistics at protein-protein interfaces (SSE elements, buried surface area, , B factor values, etc). The amino-acids supporting these annotations are obtained from Voronoi interface models. The benefit of MISA is to collate annotated sequences of (homologous) chains found in different biological contexts i.e.bound with different partners or unbound. The aggregated views MISA/SSE, MISA/BSA, MISA/ etc make it trivial to identify commonalities and differences between chains, to infer key interface residues, and to understand where conformational changes occur upon binding. As such, they should prove of key relevance for knowledge based annotations of protein databases such as the Protein Data Bank.
Illustrations are provided on the receptor binding domain (RBD) of coronaviruses, in complex with their cognate partner or (neutralizing) antibodies. MISA computed with a minimal number of structures complement and enrich findings previously reported.
The corresponding package is available from the
Structural Bioinformatics Library (https://
and https://
7.1.2 Modeling the efflux mechanism of AcrB
Participant: F. Cazals, M. Simsir.
In collaboration with I. Broutin (Univ. Paris Descartes and CNRS), and I. Mus-Veteau (Université Côte d'Azur and IPMC/CNRS).
RND family proteins are transmembrane proteins identified as large spectrum drug transporters involved in multi-drug resistance. A prototypical case in this superfamily, responsible for antibiotic resistance in selected gram negative bacteria, is AcrB. AcrB forms a trimer using the proton motive force to efflux drugs, implementing a functional rotation mechanism. Unfortunately, the size of the system (1049 amino-acid per monomer and membrane) has prevented a systematic dynamical exploration, so that the mild understanding of this coupled transport jeopardizes our ability to counter it.
The large number of crystal structures of AcrB prompts studies to further our understanding of the mechanism. To this end, we present 24 a novel strategy based on two key ingredients which are to study dynamics by exploiting information embodied in the numerous crystal structures obtained to date, and to systematically consider subdomains, their dynamics, and their interactions. Along the way, we identify the subdomains responsible for dynamic events, refine the states (A,B,E) of the functional rotation mechanism, and analyze the evolution of intramonomer and intermonomer interfaces along the functional cycle.
Our analysis shows the relevance of AcrB's efflux mechanism as a template within the HAE1 family but not beyond. It also paves the way to targeted simulations exploiting the most relevant degrees of freedom at certain steps, and also to a targeting of specific interfaces to block the drug efflux.
Our work shows that complex dynamics can be unveiled from static snapshots, a strategy that may be used on a variety of molecular machines of large size.
7.2 Modeling the flexibility of macro-molecules
Keywords: protein, flexibility, collective coordinate, conformational sampling dimensionality reduction.
7.2.1 Wang-Landau Algorithm: an adapted random walk to boost convergence
Participant: F. Cazals, A. Chevallier.
The Wang-Landau (WL) algorithm is a recently developed stochastic algorithm computing densities of states of a physical system, and also performing numerical integration in high dimensional spaces. Since its inception, it has been used on a variety of (bio-)physical systems, and in selected cases, its convergence has been proved. The convergence speed of the algorithm is tightly tied to the connectivity properties of the underlying random walk.
In this work 16, we propose an efficient random walk that uses geometrical information to circumvent the following inherent difficulties: avoiding overstepping strata, toning down concentration phenomena in high-dimensional spaces, and accommodating multidimensional distributions. These improvements are especially well suited to improve calculations on a per basin basis – included anharmonic ones.
Experiments on various models stress the importance of these improvements to make WL effective in challenging cases. Altogether, these improvements make it possible to compute density of states for regions of the phase space of small biomolecules.
7.2.2 A generic software framework for Wang-Landau type algorithms
Participant: F. Cazals, A. Chevallier.
The Wang-Landau (WL) algorithm is a stochastic algorithm designed to compute densities of states of a physical system. Is has also been recently used to perform challenging numerical integration in high-dimensional spaces. Using WL requires specifying the system handled, the proposal to explore the definition domain, and the measured against which one integrates. Additionally, several design options related to the learning rate must be provided.
This work 22 presents the first generic (C++) implementation providing all such ingredients. The versatility of the framework is illustrated with a variety of problems including the computation of density of states of physical systems and biomolecules, and the computation of high dimensional integrals. Along the way, we that integrating against a Boltzmann like measure to estimate DoS with respect to the Lebesgue measure can be beneficial.
We anticipate that our implementation, available in the Structural Bioinformatics Library (http://sbl.inria.fr), will leverage experiments on complex systems and contribute to unravel free energy calculations for (bio-)molecular systems.
7.3 Algorithmic foundations
Keywords: Computational geometry, computational topology, optimization, data analysis.
7.3.1 Fréchet mean and -mean on the unit circle: characterization, decidability, and algorithm
Participant: F. Cazals, T. O'Donnell.
In collaboration with B. Delmas (INRAe, Jouy-en-Josas).
The center of mass of a point set lying on a manifold generalizes the celebrated Euclidean centroid, and is ubiquitous in statistical analysis in non Euclidean spaces. In 21, we give a complete characterization of the weighted -mean of a finite set of angular values on , based on a decomposition of such that the functional of interest has at most one local minimum per cell. This characterization is used to show that the problem is decidable for rational angular values –a consequence of Lindemann's theorem on the transcendence of , and to develop an effective algorithm parameterized by exact predicates. A robust implementation of this algorithm based on multi-precision interval arithmetic is also presented. This implementation is effective for large values of and . Experiments on random sets of angles and protein dihedral angles consistently show that the Fréchet mean () yields a variance reduction of with respect to the classically used circular mean.
Our derivations are of interest in two respects. First, efficient -mean calculations are relevant to develop principal components analysis on the flat torus encoding angular spaces–a particularly important case to describe molecular conformations. Second, our two-stage strategy stresses the interest of combinatorial methods for p-means, also emphasizing the role of numerical issues.
The implementation is available in the Structural Bioinformatics Library (http://sbl.inria.fr).
7.3.2 Improved polytope volume calculations based on Hamiltonian Monte Carlo with boundary reflections and sweet arithmetics
Participant: F. Cazals, A. Chevallier.
In collaboration with S. Pion IMS (Univ. Bordeaux / Bordeaux INP / CNRS UMR 5218).
Computing the volume of a high dimensional polytope is a fundamental problem in geometry, also connected to the calculation of densities of states in statistical physics, and a central building block of such algorithms is the method used to sample a target probability distribution.
The work 23 studies Hamiltonian Monte Carlo (HMC) with reflections on the boundary of a domain, providing an enhanced alternative to Hit-and-run (HAR) to sample a target distribution restricted to the polytope. We make three contributions. First, we provide a convergence bound, paving the way to more precise mixing time analysis. Second, we present a robust implementation based on multi-precision arithmetic – a mandatory ingredient to guarantee exact predicates and robust constructions. We however allow controlled failures to happen, introducing the Sweeten Exact Geometric Computing (SEGC) paradigm. Third, we use our HMC random walk to perform H-polytope volume calculations, using it as an alternative to HAR within the volume algorithm by Cousins and Vempala. The tests, conducted up to dimension 50, show that the HMC random walk outperforms HAR.
7.3.3 Overlaying a hypergraph with a graph with bounded maximum degree, with application for low-resoluton reconstructions of molecular assemblies
Participant: D. Mazauric.
In collaboration with F. Havet (CNRS, I3S, Inria/I3S project-team Coati) V.-H. Nguyen (Inria, Inria/I3S project-team Coati), and R. Watrigant (Univ. Lyon).
In the article 18, we analyze a generalization of the minimum connectivity inference problem (MCI). MCI models the computation of low-resolution structures of macro-molecular assemblies, based on data obtained by native mass spectrometry. The generalization studied in this article, allows us to consider more refined constraints for the characterization of low resolution models of large assemblies. We model this problem by using hypergraphs: for a (possibly infinite) fixed family of graphs , we say that a graph overlays on a hypergraph if is equal to and the subgraph of induced by every hyperedge of contains some member of as a spanning subgraph. While it is easy to see that the complete graph on overlays on a hypergraph whenever the problem admits a solution, the Minimum -Overlay problem asks for such a graph with at most edges, for some given . This problem allows to generalize some natural problems which may arise in practice. For instance, if the family contains all connected graphs, then Minimum -Overlay corresponds to the MCI problem.
Let and be respectively a graph and a hypergraph defined on a same set of vertices, and let be a fixed graph. We say that -overlays a hyperedge of if is a spanning subgraph of the subgraph of induced by , and that it -overlays if it -overlays every hyperedge of . In this article, we study the computational complexity of two new problems, taking into account degree constraints (for example a protein cannot have many other proteins in its neighborhoud). The first problem, -Overlay, consists in deciding whether there is a graph with maximum degree at most that -overlays a given hypergraph . It is a particular case of the second problem Max -Overlay, which takes a hypergraph and an integer as input, and consists in deciding whether there is a graph with maximum degree at most that -overlays at least hyperedges of . We give a complete polynomial/NP-complete dichotomy for the Max --Overlay problems depending on the pairs , and establish the complexity of -Overlay for many pairs .
7.3.4 Sequential metric dimension
Participant: D. Mazauric.
In collaboration with J. Bensmail (I3S, Inria/I3S project-team Coati) and F. Mc Inerney (Inria/I3S project-team Coati) and N. Nisse (Inria, Inria/I3S project-team Coati) and S. Pérennes (CNRS, Inria/I3S project-team Coati).
In the localization game, introduced by Seager in 2013, an invisible and immobile target is hidden at some vertex of a graph . At every step, one vertex of can be probed which results in the knowledge of the distance between and the secret location of the target. The objective of the game is to minimize the number of steps needed to locate the target whatever be its location.
In the article 14, we address the generalization of this game where vertices can be probed at every step. Our game also generalizes the notion of the metric dimension of a graph. Precisely, given a graph and two integers , the localization problem asks whether there exists a strategy to locate a target hidden in in at most steps and probing at most vertices per step. We first show that, in general, this problem is NP-complete for every fixed (resp., ). We then focus on the class of trees. On the negative side, we prove that the localization problem is NP-complete in trees when and are part of the input. On the positive side, we design a -approximation for the problem in -node trees, i.e., an algorithm that computes in time (independent of ) a strategy to locate the target in at most one more step than an optimal strategy. This algorithm can be used to solve the localization problem in trees in polynomial time if is fixed. We also consider some of these questions in the context where, upon probing the vertices, the relative distances to the target are retrieved. This variant of the problem generalizes the notion of the centroidal dimension of a graph.
7.3.5 Distributed link scheduling
Participant: D. Mazauric.
In collaboration with J.-C. Bermond (I3S, Inria/I3S project-team Coati), V. Misra (Columbia University), and P. Nain (Inria, Inria project-team Neo).
In the article 15, we investigate distributed transmission scheduling in wireless networks. Due to interference constraints, “neighboring links” cannot be simultaneously activated, otherwise transmissions will fail. Here, we consider any binary model of interference. We use a model described by Bui, Sanghavi, and Srikant. We assume that time is slotted and during each slot there are two phases: one control phase in which a link scheduling algorithm determines a set of non interfering links to be activated, and a data phase in which data is sent through these links. We assume random arrivals on each link during each slot, so that a queue is associated to each link. Since nodes do not have a global knowledge of the queues sizes, our aim is to design a distributed link scheduling algorithm. To be efficient the control phase should be as short as possible; this is done by exchanging control messages during a constant number of mini-slots (constant overhead).
In this paper, we design the first fully distributed local algorithm with the following properties: it works for any arbitrary binary interference model; it has a constant overhead (independent of the size of the network and the values of the queues), and it does not require any knowledge of the queue-lengths. We prove that this algorithm gives a maximal set of active links, where for any non-active link there exists at least one active link in its interference set. We also establish sufficient conditions for stability under general Markovian assumptions. Finally, the performance of our algorithm (throughput, stability) is investigated and compared via simulations to that of previously proposed schemes.
8 Partnerships and cooperations
8.1 Regional initiatives
– Frédéric Cazals is endowed chair within
the 3IA Côte d'Azur (https://
9 Dissemination
9.1 Promoting scientific activities
9.1.1 Scientific events: organisation
- Frédéric Cazals co-organized the winter school Algorithms in Structural Bioinformatics, Intrinsic Disorder in Protein: From Non-Folding to Fuzzy Recognition to Phase Separation, CNRS center of Cargèse, November 23rd–27th. Unfortunately, the school was canceled due to the pandemics.
- Frédéric Cazals co-organized the Symposium Multidisciplinary approaches in cancer research, Inria Sophia, Nov. 16-17, 2020. Unfortunately, the school was canceled due to the pandemics.
Member of the conference program committees
– Frédéric Cazals was member of the following program committees:
- Symposium on Solid and Physical Modeling
- Intelligent Systems for Molecular Biology (ISMB)
Reviewer - reviewing activities
– Frédéric Cazals reviewed for the following journals:
- Bioinformatics
- eLife
- Graphical models
- Journal of Chemical Physics
- Proteins: structure, function, bioinformatics
9.1.2 Invited talks
– Frédéric Cazals gave the following invited talks:
- Comparing (interface) models: a multivariate data analysis perspective, Elixir - 3DBioInfo, Cambridge (visio-conference), November 2020.
- Multiple Interface String Alignments: Boosting the analysis of protein interfaces, with applications to the SARS-Cov-2 spike, GDR BIM/GT MASIM, meeting dedicated to SARS-Cov-2, November 2020.
- Clustering algorithms for structural studies: insights on novel metrics and cluster stability assessment, Algorithms for integrative structural biology, Grenoble, March 2020.
9.1.3 Leadership within the scientific community
– Frédéric Cazals:
- 2010-.... Member of the steering committee of the GDR Bioinformatique Moléculaire, for the Structure and macro-molecular interactions theme.
- 2017-.... Co-chair, with Yann Ponty, of the working group /
groupe de travail (GT MASIM - Méthodes Algorithmiques pour les
Structures et Interactions Macromoléculaires, within the GDR
de BIoinformatique Moléculaire (GDR BIM,
https://
www. gdr-bim. cnrs. fr/).
9.1.4 Scientific expertise
– Frédéric Cazals:
- 2020: member of the IUF senior panel.
9.1.5 Research administration
– Frédéric Cazals:
- 2018-...: Member of the bureau du comité des équipes projets.
- 2020-...: Member of the bureau of the EUR Life, Université Côte d'Azur.
9.2 Teaching - Supervision - Juries
9.2.1 Teaching
- Master: Data Sciences Program, Department of Applied Mathematics, Ecole Centrale-Supélec:
Frédéric Cazals (Inria ABS) and Frédéric Chazal (Inria Saclay),
Foundations of Geometric Methods in Data Analysis,
Web: http://
www-sop. inria. fr/ abs/ teaching/ centrale-FGMDA/ centrale-FGMDA--cazals-carriere-2020-2021. html - Master: Frédéric Cazals (Inria ABS), Understanding biomolecular interactions and simulations: a primer in statistical physics for biomolecules, Polytech Nice Sophia, Université Côte d'Azur, Master Bio-informatique.
- Master : Dorian Mazauric, Algorithmique et Complexité, 23h30 TD, niveau M1, Polytech Nice Sophia, Université Côte d'Azur, filière Sciences Informatiques, France.
9.2.2 Supervision
- PhD in progress, 3rd year: Méliné Simsir, Modeling drug efflux by Patched. Université Côte d'Azur. Thesis co-supervised by Frédéric Cazals and Isabelle Mus-Veteau, IPMC/CNRS.
- PhD in progress, 2nd year: Timothée O'Donnel, Modeling the influenza polymerase. Université Côte d'Azur. Thesis co-supervised by Frédéric Cazals and Bernard Delmas, INRAe Jouy-en-Josas.
- PhD in progress, 2nd year : Thi Viet Ha Nguyen, Graph Algorithms techniques for (low and high) resolution models of large protein assemblies, Frédéric Havet (Inria/I3S project-team Coati) and Dorian Mazauric.
9.2.3 Juries
– Frédéric Cazals:
- Julien Bensmail, Habilitation thesis, Université Côte d'Azur, December 2020. Committee member (president) for the habilitation Contribution aux ponderations distinguantes de graphes.
- Meline Simsir, PhD thesis, Université Côte d'Azur, December 2020. Committee member (co-supervisor) for the PhD thesis Structural modeling of RND family efflux pumps : from antibio-resistance to chemotherapy resistance
- Siddarth Pritam, PhD thesis, Université Côte d'Azur, March 2020. Committee member (president) for the thesis Collapses and Persistent Homology.
- Shard Goulam Abas, PhD thesis, U. Paris-Saclay, April 2020. Rapporteur on the thesis Développement de méthodes mathématiques pour l’analyse de trajectoires conformationnelles en dynamique moléculaire. Advisors: A. Trouvé (U. Paris-Saclay), L. Tchertanov (CNRS).
9.3 Popularization
9.3.1 Internal or external Inria responsibilities
– Dorian Mazauric:
- 2019-.... Head of Commission Mastic (Médiation et Animation des MAthématiques, des Sciences et Techniques Informatiques et des Communications), Inria Sophia Antipolis - Méditerranée.
- 2019-.... Coordinator of Terra Numerica – vers une Cité du Numérique (https://
terra-numerica. org), an ambitious scientific popularisation project. Its main goal is to create a "Dedicated Digital space" in the south of France, (in the spirit of the "Cité des Sciences" or "Palais de la découverte" in Paris). To do so, Terra Numerica is developing and structuring popularisation activities, supports which are available at the Maison de l'Intelligence Artificielle and also spread in different antennas throughout the territory (e.g. in schools, exhibition extensions...). This large-scale project involves (brings together) all the actors of research, education, industry, associations and collectivities... It is actually composed of more than one hundred people. - 2018-.... Member of the Conseil d'Administration de l'association les Petits Débrouillards.
- 2017-.... Member of projet de médiation Galéjade : Graphes et ALgorithmes : Ensemble de Jeux À Destination des Ecoliers... (mais pas que).
9.3.2 Interventions
– Dorian Mazauric:
- 03-04/10/2020 : Ateliers et conférence au village des sciences de Villeneuve-Loubet. Fête de la Science 2020.
- 14/08/2020 : Intervention stages Découverte des métiers du Numérique des Petits Débrouillards. Ariane, Nice.
- 12/02/2020 : Formation d’une centaine d’enseignants de cycle 1 de la circonscription d’Antibes. Algorithmes et graphes.
- 08/02/2020 : Forum des métiers au lycée Hutinel, Cannes-la-Bocca. Organisé par Rotary Club Palm Beach. Présentation des métiers en sciences du numérique.
- 04/02/2020 : Conférence au collège Sydney Bechet, Antibes Juan-les-Pins. Algorithmes.
- 28/01/2020 : Journée de formation organisée par Canopé à Toulon. Thème de la journée : robotique éducative et apprentissages fondamentaux – défis robotiques déclinés pour tous les niveaux, adossés aux apprentissages disciplinaires et transversaux. Graphes, algorithmes et magie des mathématiques et de l’informatique.
10 Scientific production
10.1 Major publications
- 1 inproceedingsConnectivity Inference in Mass Spectrometry based Structure DeterminationEuropean Symposium on Algorithms (Springer LNCS 8125)Sophia Antipolis, FranceSpringer2013, 289--300URL: http://hal.inria.fr/hal-00849873
- 2 articleUnveiling Contacts within Macro-molecular assemblies by solving Minimum Weight Connectivity Inference ProblemsMolecular and Cellular Proteomics142015, 2274--2282URL: https://hal.science/hal-01078378
- 3 articleEnergy landscapes and persistent minimaThe Journal of Chemical Physics14452016, 4URL: https://www.repository.cam.ac.uk/handle/1810/253412
- 4 inproceedingsMolecular shape analysis based upon the Morse-Smale complex and the Connolly functionACM SoCGSan Diego, USA2003, 351-360
- 5 articleConformational Ensembles and Sampled Energy Landscapes: Analysis and ComparisonJ. of Computational Chemistry36162015, 1213--1231URL: https://hal.science/hal-01076317
- 6 articleGreedy Geometric Algorithms for Collections of Balls, with Applications to Geometric Approximation and Molecular Coarse-GrainingComputer Graphics Forum3362014, 1--17URL: http://hal.inria.fr/hal-00777892
- 7 articleThe Structural Bioinformatics Library: modeling in biomolecular science and beyondBioinformatics7332017, 1--8URL: http://sbl.inria.fr
- 8 bookF. CazalsP. KornprobstModeling in Computational Biology and Medicine: A Multidisciplinary EndeavorSpringer2013, URL: http://hal.inria.fr/hal-00845616
- 9 articleAssessing the Reconstruction of Macro-molecular Assemblies with Toleranced ModelsProteins: structure, function, and bioinformatics8092012, 2125--2136
- 10 articleProbing a Continuum of Macro-molecular Assembly Models with Graph Templates of Sub-complexesProteins: structure, function, and bioinformatics81112013, 2034--2044URL: http://hal.inria.fr/hal-00849795
- 11 articleCharacterizing the Morphology of Protein Binding PatchesProteins: structure, function, and bioinformatics80122012, 2652--2665
- 12 articleHigh Resolution Crystal Structures Leverage Protein Binding Affinity PredictionsProteins: structure, function, and bioinformatics1842015, 9--20URL: https://hal.inria.fr/hal-01159641
- 13 articleHybridizing rapidly growing random trees and basin hopping yields an improved exploration of energy landscapesJ. Comp. Chem.3782016, 739--752URL: https://hal.inria.fr/hal-01191028
10.2 Publications of the year
International journals
International peer-reviewed conferences
Reports & preprints
10.3 Cited publications
- 25 articleDetermining the architectures of macromolecular assembliesNature450Nov 2007, 683-694
- 26 articleThe molecular architecture of the nuclear pore complexNature45071702007, 695--701
- 27 articleIntegrating Diverse Data for Structure Determination of Macromolecular AssembliesAnn. Rev. Biochem.772008, 11.1--11.35
- 28 book Computational Biochemistry and Biophysics M. Dekker 2001
- 29 articleA Hidden Markov Model derived structural alphabet for proteinsJ. Mol. Biol.2004, 591-605
- 30 articleAnalytical molecular surface calculationJ. Appl. Crystallogr.1651983, 548--558
- 31 articleRotamer libraries in the 21st centuryCurr Opin Struct Biol1242002, 431-440
- 32 articleExtent of Hydrogen-Bond Protection in Folded Proteins: A Constraint on Packing ArchitecturesBiophysical Journal832002, 2475-2481
- 33 book Structure and Mechanism in Protein Science: A Guide to Enzyme Catalysis and Protein Folding Freeman 1999
- 34 incollectionProtein geometry: volumes, areas, and distancesThe international tables for crystallography (Vol F, Chap. 22)Springer2001, 531--539
- 35 articleStatistical potentials and scoring functions applied to protein-ligand bindingCurr. Op. Struct. Biol.112001, 231-235
- 36 articleConformations of amino acid side chains in proteinsJ. Mol. Biol.1251978, 357--386
- 37 articleHidden complexity of free energy surfaces for peptide (protein) foldingPNAS101412004, 14766-14770
- 38 incollection Metastable Conformational Structure and Dynamics: Peptides between Gas Phase and Aqueous Solution Analysis and Control of Ultrafast Photoinduced Reactions. Series in Chemical Physics 87 Springer 2007
- 39 articleOn Itinerant Water Molecules and Detectability of Protein-Protein Interfaces through Comparative Analysis of HomologuesJMB36922007, 584--595
- 40 articleIntegrating statistical pair potentials into protein complex predictionProteins692007, 511--520
- 41 book Geometry and Topology in Hamiltonian Dynamics and Statistical Mechanics Springer 2007
- 42 articleFast and Reliable Analysis of Molecular Motion Using Proximity Relations and Dimensionality ReductionProteins: Structure, Function, and Bioinformatics6742007, 897--907
- 43 articleAnchor residues in protein-protein interactionsPNAS101312004, 11287-11292
- 44 articleFrom The Cover: The modular architecture of protein-protein binding interfacesPNAS10212005, 57-62
- 45 articleAreas, volumes, packing and protein structureAnn. Rev. Biophys. Bioeng.61977, 151-176
- 46 articleTopographical complexity of multidimensional energy landscapesPNAS103492006, 18551-18555
- 47 articleFolding and binding: an extended family businessCurrent Opinion in Structural Biology1512005, 1--3
- 48 articleCalculation of Conformational Ensembles from Potential of Mean Force: An Approach to the Knowledge-based prediction of Local Structures in Globular ProteinsJ. Mol. Biol.2131990, 859-883
- 49 articleAn atomic environment potential for use in protein structure predictionJMB35242005, 986--1001
- 50 articleStructural basis of macromolecular recognitionAdv. in protein chemistry612002, 9--73

